Abstract
Content:
- Objective
- Idea
- Actuality
- The influence of cutting depth on the vibration frequency
- Mathematic model of oscillation system
- Conclusion
- References
NOTE: This abstract was created on 14 of May, 2012, i.e. before finishing the master's research paper. Approximate completion date – 15 of September, 2012.
Objective
The objective of my work is creating of complex mathematic model of cutting vibrations and comparison of the results with experimental data of other authors.
Idea
The main idea of my work is: in turning process instantaneous values of cutting parameters vary due to the oscillations, which causes the variability of cutting force. On this basis, the state of a dynamical system in every point of time is considered definitely dependent on instantaneous values of cutting parameters through the cutting force.
Actuality
Recently, a tendency to high-speed machining has been occurred in machine-building, which allows saving the main non-renewable resource - time. The main reasons for limiting the cutting parameters are the vibrations that occur at any machining, including turning. Therefore, the priority task of modernity is searching for causes of vibrations and avoiding of them.
The oscillations, which occur in the process of the turning, influence on the parameters of quality and accuracy of machined surface. The mathematical description of this process gives the opportunity to predict cutting parameters, which allow avoiding adverse dynamic conditions.
The influence of cutting depth on the vibration frequency
For analyzing the influence of cutting depth on the vibration frequency, we need to consider the idealized scheme of turning a cylindrical work piece (fig. 1), that oscillate in the radial direction.
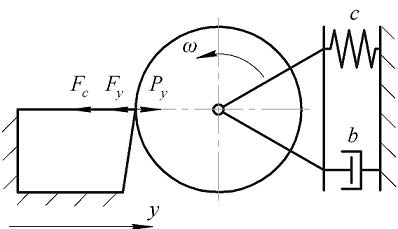
Figure 1. The scheme of dynamic cutting system with one (radial) degree of freedom
From the calculations it can be concluded that the influence of cutting depth on the cyclic frequency of radial vibration decreases because of static stiffness increase.
Cutting depth t0, mm |
Сyclic frequency ω, rad/sec, with static stiffness coefficient с, N/m: |
|||
|---|---|---|---|---|
105 |
106 |
107 |
108 |
|
1 |
200 |
298 |
761 |
2341 |
2 |
194 |
294 |
759 |
2340 |
3 |
191 |
292 |
758 |
2340 |
4 |
188 |
291 |
758 |
2340 |
5 |
186 |
289 |
757 |
2339 |
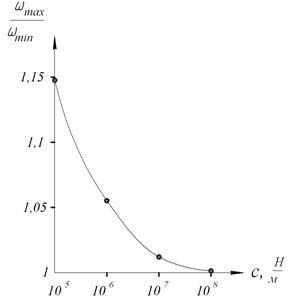
Figure 2. Dependence of cyclic frequency variation on work piece static stiffness: ωmax – cyclic frequency with t0=0,2 mm, ωmin – cyclic frequency with t0=5 mm
From the figure 2 we can conclude, that static stiffness c influences on frequency more, than dynamic "stiffness" that includes cutting depth.
Mathematic model of oscillation system
To create the mathematic model of oscillation system the following scheme was considered.
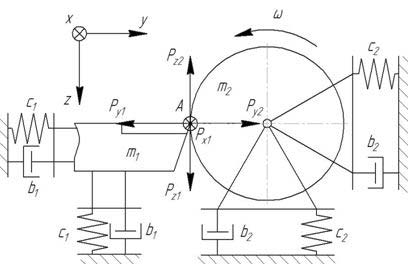
Figure 3. The general scheme of cutting oscillation system (axial degree of freedom of cutting tool and degree of freedom of work piece torsional vibrations are not illustrated)
Movement and movement speed of work piece and cutting tool define instantaneous values of cutting parameters (fig. 4).
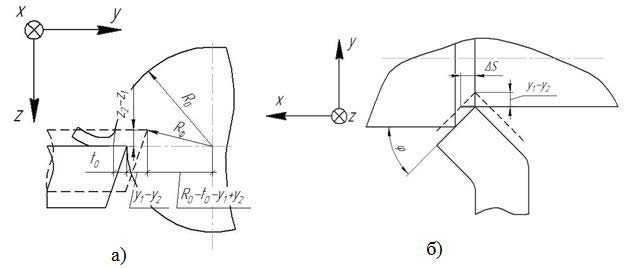
Figure 4 – Scheme for defining instantaneous values of cutting speed, cutting depth (a) and feed (b)
According to the above schemes dependences of instantaneous values of cutting parameters on small movements and there speeds were derived:
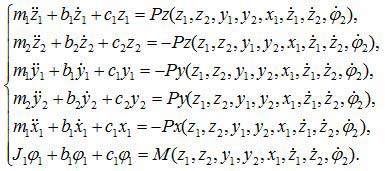
Created mathematic model do not contradict the experimental data according to such criteria as:
- digging radial force is bigger, than repulsion one, i.e. radial force do not define with radial movement of cutting tool and work piece;
- radial and tangential forces changes in-phase.
Conclusion:
Created mathematic model accurately describes the dynamic turning system. It confirms the assumption that the vibrations in metal cutting are not forced (except when there is an external driving force), but represent a process caused by the cutting. I.e., cutting vibrations are self-excited oscillations.
References
- Каширин А. И. Исследование вибраций при резании металла. – М.: Академия наук СССР, 1944. – 131 с.
- Амосов И. С. Осциллографическое исследование вибраций при резании металлов. – М.: Машгиз, 1951. – 64 с.
- Манжос Г. А. Исследование вибраций в условиях скоростного точения и изыскание методов борьбы с ними. – М.: Машгиз, 1951. – 47 с.
- Соколовский А. П. Научные основы технологии машиностроения / А. П. Соколовский. - М.: Машгиз, 1955. - 516 с.
- Ильницкий И. И. Колебания в металлорежущих станках и пути их устранения. М.: Машгиз, 1958. – 141 с.
- Жарков И. Г. Вибрации при обработке лезвийным инструментом / И. Г. Жарков. – Л.: Машиностроение, 1986. – 184 с.
- Справочник технолога-машиностроителя. В 2-х т. Т.2 / Под ред. А.Г. Косиловой и Р.К. Мещерякова.- 4-е изд., перераб. и доп. – М.: Машиностроение, 1985. 496 с.
