ДонНТУ   Портал магистров

Реферат по теме выпускной работы

Содержание

Введение

Задача восстановления пропусков (импутирования) в эмпирических таблицах является традиционной в классе задач обработки данных, таких, например, как задачи обучения распознаванию образов [1].  Традиционными причинами, приводящими к появлению пропусков, являются невозможность получения или обработки данных, искажение или сокрытие информации [2]. Объективными причинами этого являются поломки оборудования при измерении тех или иных характеристик, потеря или ограничение доступа к информации и другие [3]. Субъективные причины обусловлены человеческим фактором при накоплении и обработке информации вследствие влияния психологических аспектов и особенностей памяти или умышленного сокрытия информации [4]. Так в промышленном эксперименте некоторые результаты могут отсутствовать вследствие поломок оборудования, не связанных с экспериментом. При опросе общественного мнения часть опрашиваемых, возможно, не окажет предпочтения одному кандидату перед другим или не откажется от предоставления данных о своих доходах. В результате на вход программ анализа собранных данных поступают неполные сведения.

Наличие пропусков в данных, так же как и анализ только полных наблюдений (после исключения наблюдений с пропусками), может привести к  получению смещенных результатов, и как следствие к искажению выводов, которые могут быть сделаны по результатам исследования, и принятию неверных стратегических решений [5]. Именно поэтому задача восстановления пропусков в данных является одним из приоритетных направлений анализа данных для построения эффективных интеллектуальных систем.

1. Цель и задачи исследования

Объектом исследования является задача восстановления пропусков в эмпирических таблицах данных.

Предметом исследования – методы заполнения пропусков в данных.

Целью выпускной работы магистра является разработка метода заполнения пропусков в эмпирических данных на основе взвешенных обучающих выборок.

В процессе работы необходимо решить следующие задачи:

1) исследовать существующие алгоритмы заполнения пропусков в эмпирических данных, критерии оценки качества восстановленных данных;

2) исследовать методы построения взвешенных выборок;

3) разработать метод  заполнения пропусков в данных на основе взвешенных обучающих выборок;

4) разработать прототип программной системы тестирования алгоритмов восстановления пропусков в эмпирических таблицах данных;

5) выполнить сравнительный анализ предложенного алгоритма и известных алгоритмов решения данной задачи.

2. Предполагаемая научная новизна

Научной новизной данной работы является разработка метода заполнения пропусков в эмпирических данных на основе взвешенных обучающих выборок. Поскольку принцип построения взвешенных обучающих выборок, как и многих алгоритмов заполнения пробелов в данных, состоит в усреднении значений признаков выбранного локального подмножества данных, предполагается, что на основе взвешенных выборок может быть построен эффективный алгоритм импутирования данных.

3. Практическая значимость

С проблемой обработки пропусков в массивах данных приходится сталкиваться при проведении разнообразных социологических, экономических и статистических (технических, медицинских, геологических и др.) исследований. Восстановление пропусков в данных также используется в задачах нормализации временных рядов с пропущенными наблюдениями [6] и поиска близких по эмпирическим данным объектов.

В некоторых прикладных задачах количество строк таблицы данных, соответствующих объектам исследования, в которых имеются пропущенные данные, достигает 40%. Отсутствие в системе алгоритма восстановления пропусков в данных приведет к необходимости удаления этих объектов и, как следствие, существенному уменьшению априорной информации и ухудшению эффективности работы системы в целом.

4. Проблема неполных данных и анализ методов её решения

Пусть исходные данные представлены в виде матрицы 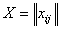 (таблица 1), строки которой соответствуют l изучаемым объектам, а столбцы представляют собой данные по m переменным, измеряемые для каждого объекта. Элементы матрицы , где , 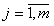являются действительными числами – значениями непрерывных (например, время или размер дохода), дискретных или категориальных переменных (например, пол человека). В свою очередь категориальные признаки могут быть упорядоченными (например, образование) или неупорядоченными (раса, пол).

Причины пропусков данных могут быть самыми разными [7], поэтому знание механизма, приводящего к отсутствию значений, является ключевым при выборе методов анализа и интерпретации результатов. Механизм порождения пропусков дает понимание степени важности потерянной информации, ведь неполные данные несут в себе новую информацию, необходимую для исследования, поэтому их важно включать в анализ.

4.1 Виды пропусков в данных

На сегодняшний день создано значительное число методов восстановления пропусков, обзор которых содержится, например в [2], однако единая методология обработки подобных данных отсутствует, несмотря на ее необходимость. Возможность использования методов разной степени сложности связана с тем, насколько простым или сложным является механизм, согласно которому данные оказываются пропущенными.

Согласно [2, 8], выделяют следующие виды пропусков в данных:

1) полностью случайные пропуски (data are missing completely at random – MCAR), если условная вероятность 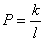, где k – количество строк таблицы, содержащих пропущенное значение, P не зависит ни от самого пропущенного значения переменной, ни от значений прочих переменных (эта вероятность постоянна для всех наблюдений);

 2) пропуски в данных называются случайными (missing at random – MAR), если вероятность P не зависит от самого пропущенного значения переменной, но может зависеть от значений других переменных (в этих случаях механизм пропусков несущественен  и к данным применимо большинство методов восстановления пропусков);

3) пропуски являются существенными, если вероятность P зависит от самого пропущенного значения переменной (механизм пропусков является существенным и для корректного анализа данных необходимо знать этот механизм).

Введенные понятия относятся к отдельным переменным, и в пределах одной и той же таблицы данных можно наблюдать все приведенные виды пропусков в данных. Необходимо отметить, что определение вида пропусков зачастую не представляется возможным.

4.2 Виды алгоритмов импутирования данных

Существуют два подхода к решению проблемы неполных данных.

Первый подход состоит в исключении строк, содержащих пропущенные данные. Данный метод легко реализуем, но необходимым условием его применения является следование данных требованию MCAR, т.е. пропуски в данных по переменным должны быть полностью случайными. Кроме того, он обычно применяется лишь при незначительном количестве пропусков в таблице, иначе полученная на выходе таблица данных становится непредставительной. Главный недостаток такого подхода обусловлен потерей информации при исключении неполных данных.

Второй подход состоит в заполнении пропусков на основе анализа имеющихся эмпирических данных. Классификация методов импутирования данных [9] приведена на рисунке 1. Далее приведем их описание и особенности использования.

Классификация методов импутирования данных

Рисунок 1 – Классификация методов импутирования данных

 

1. Заполнение пропусков значениями переменных таблицы данных. Значение переменной рассчитывается по всей таблице или по выделенной локальной группе. Наиболее часто используют следующие алгоритмы  данного типа [2, 7]:

- заполнение средними – рассчитывается по присутствующим значениям переменной по всей таблице;

- заполнение с пристрастным подбором – пропуски заполняются значениями, полученными для другого сходного объекта выборки (подстановка выбирается для каждого пропущенного значения по оценке распределения);

- подстановка с подбором внутри групп – формируются группы  и пропуски в каждой группе заполняются присутствующими значениями из нее;

- подбор ближайшего соседа (метод Hot Desk) – по заданной метрике определяется ближайший к заполняемому объект по всем присутствующим значениям переменных, и пропуск заполняется значением соответствующей переменной ближайшего объекта;

- заполнение по регрессии – по комплектным данным строится уравнение линейной множественной регрессии и вычисляются пропущенные значения переменной. При использовании метода многомерной регрессии строится модель линейной зависимости переменной, в которой необходимо заполнить пропуски, от ряда других имеющихся признаков. Регрессионные коэффициенты для каждого из предикторов находятся методом наименьших квадратов в массиве с полными данными. Подставляя значения предикторов в регрессионное уравнение, получают прогноз пропущенного показателя;

- заполнение значением переменной случайно выбранного объекта;

- многократное заполнение с подбором значения переменной по заданным критериям;

- составные методы.

2. Заполнение пропусков на основе моделирования. Выполняется построение модели порождения пропусков. Выводы получают с помощью функции правдоподобия, построенной при условии справедливости этой модели, с оцениванием параметров методами типа максимального правдоподобия.

Наиболее эффективным методом моделирования является ЕМ-алгоритм [2, 9]. Метод максимизации ожиданий (ЕМ  – expectation   maximization) , в некоторых источниках так же называемый  ЕМ  – оцениванием, представляет собой итерационную процедуру, предназначенную для  решения задач оптимизации некоторого функционала, через аналитический поиск экстремума целевой функции.

На первом этапе Е (expectation) по совокупности имеющихся абсолютно полных или частично (по целевой переменной)  полных  наблюдений рассчитываются условные ожидаемые значения  целевой переменной для каждого неполного наблюдения.  Затем после получения массива полных наблюдений, оцениваются основные статистические параметры: меры средней тенденции и разброса, показатели взаимной корреляции и ковариации переменных. В случае работы с неполными даными на Е – этапе определяется функция условного математического ожидания логарифма полной функции правдоподобия при известном значении целевой переменной Х.

На втором этапе  М (maximization), задача алгоритма максимизировать степень взаимного соответствия ожидаемых и реально подставляемых данных, а также соответствия структуры импутированных данных структуре данных полных наблюдений.

3. Resampling метод [4, 7]. Метод Resampling основывается на  бутстреп-подходе, который предполагает многократную обработку различных частей одних и тех же данных и сопоставление полученных таким образом результатов.

Суть алгоритма Resampling заключается в том, что значения для пропусков выбираются из имеющихся случайным образом, с возвращением (когда значение может использоваться еще раз после выбора) или без него. После этого на всем массиве строится регрессионная модель, позволяющая предсказать значения для пробелов. Для всех предполагаемых предикторов находятся регрессионные коэффициенты и константа. Затем вычисляются итоговые значения регрессионных коэффициентов, по которым и будут предсказаны окончательные пропущенные значения.

Преимуществом данного метода является повторное использование исходных данных, ведь увеличение числа подвыборок позволяет наиболее полно использовать исходную информацию. С другой стороны, объем новой информации уменьшается для каждой новой подвыборки, так как увеличивается вероятность того, что данные элементы выборки были уже выбраны раньше, – это основной недостаток метода вкупе с отсутствием процедур его оптимизации.

4. Локальные алгоритмы восстановления пропусков (алгоритмы Zet и ZetBraid) [5, 10]. Алгоритмы семейства Zet (Wanga) и ZetBraid, по сути, являются детально проработанной и апробированной технологией верификации экспериментальных данных, основанной на гипотезе их избыточности. Внешне они сходны с методом локального заполнения.

Суть алгоритма Zet  заключается в подборе для каждого пропуска импутируемого значения не из всей совокупности полных  наблюдений, а из некоторой ее части, называемой компонентной матрицей. Она  состоит  из компонентных строк и столбцов. Компонентность  некоторой строки  или объекта представляет собой величину обратнопропорциональную декартовому расстоянию до целевой строки (неполного наблюдения с пропуском) в пространстве, оси которого заданы переменными  – рассматриваемыми характеристиками объектов.

По данным  компонентной матрицы затем строится функциональная зависимость прогнозируемого значения от соответствующего значения в компетентной матрице, на основе которой, затем, прогнозируется значение пропуска.

Основное отличие и одновременно достоинство алгоритма   ZetBraid (плетение) от алгоритма Zet  заключается в том,  что в нем заложен аппарат для объективного определения размерности компонентной матрицы. В процессе работы алгоритма происходит последовательный поочередный отбор компетентных строк и компетентных столбцов. При каждом новом отборе строки или столбца формируется новая компетентная матрица. По заданному критерию определяется ее эффективность при прогнозировании пропусков.

Также существуют нейросетевые и эволюционные алгоритмы заполнения пропусков в данных [4, 11].

Необходимо также отметить, что помимо очевидных достоинств, импутирование, как способ решения проблемы недостающей информации имеет несколько недостатков, которые нельзя не учитывать [9]:

1) использование для  предсказания пропусков имеющихся  полных  данных искажает структуру результирующих данных (после импутирования), которая смещается в сторону структуры только полных наблюдений;

2) искусственная подстановка пропусков вносит в массив определенную долю искусственных данных, которые в свою очередь приводят к смещению значимости получаемых на их основе результатов.

Модели, построенные по восстановленным данным, могут быть менее точными по сравнению с идеальной моделью, построенной только на полных наблюдениях. Потери в их точности будут зависеть от качества  предсказания отсутствующих значений, т.е. от выбора алгоритма заполнения пропусков в данных и от объема обрабатываемых данных.

Одним из наиболее эффективных способов заполнения пропусков в данных является локальное заполнение (заполнение с подбором внутри групп). На идее выделения групп основаны и алгоритмы построения взвешенных обучающих выборок w-объектов.

5. Построение взвешенных обучающих выборок на основе метода w-baseWTS

В работе [12] предложен метод w-baseWTS построения взвешенной обучающей выборки w-объектов для сокращения выборок большого объема. Основой данного метода является выбор множеств близкорасположенных объектов исходной выборки и их замена одним взвешенным объектом новой выборки. Значения признаков каждого объекта новой выборки являются центрами масс значений признаков объектов исходной выборки, которые он заменяет. Введенный дополнительный параметр – вес определяется как количество объектов исходной выборки, которые были заменены одним объектом новой выборки. Предлагаемый метод ориентирован как на сокращение исходной обучающей выборки, так и на анализ необходимости корректировки выборки и быстрое выполнение такой корректировки при пополнении выборки в процессе работы системы.

Построение w-объекта состоит из трех последовательных этапов:

1) построение образующего множества Wf , содержащее некоторое количество d объектов исходной выборки, принадлежащих одному классу;

2) формирование вектора XiW={xi1, xi2, …, xin} значений признаков w-объекта XiWи расчет его веса pi;

3) корректировка исходной обучающей выборки – удаление объектов, включенных в образующее множество X=X\Wf.

Построение образующего множества Wf  состоит в нахождении начальной точки Xf1 формирования w-объекта, определении конкурирующей точки Xf2 и выборе в образующее множество Wf таких объектов исходной выборки, расстояние до каждого из которых от начальной точки меньше, чем расстояние от них до конкурирующей точки. В качестве начальной точки Xf1 формирования w-объекта используется объект исходной обучающей выборки, наиболее удаленный от всех объектов других классов. Конкурирующая точка Xf2 выбирается путем нахождения ближайшего к  Xf1 объекта, не принадлежащего тому же классу, что и сам  Xf1,  т.е.  yf1≠yf2.

Выбор объектов{Xf1, Xf2, …, Xd} образующего множества Wf осуществляется по следующему правилу:  объект Xi включается в Wf, если: 

1) он принадлежит тому же классу, что и начальная точка Xf1;

2) расстояние от рассматриваемого объекта до начальной точки Xf1  меньше, чем до конкурирующей точки Xf2;

3) расстояние Ri1 от рассматриваемого объекта до начальной точки меньше расстояния  Ri2  от рассматриваемого объекта до конкурирующей точки и меньше расстояния R12 между начальной и конкурирующей точками (для случая, когда классы состоят из нескольких отдельных областей признакового пространства).

Таким образом, образующее множество Wf формируется по правилу:

Принцип формирования образующего множества приведен на рисунке 2.

Значения признаков {xi1, xi2, …, xin} нового w-объекта XiWформируются по образующему множеству Wf и рассчитываются как координаты центра масс системы из pf=|Wf| материальных точек (примем, что объекты исходной обучающей выборки, являющиеся в признаковом пространстве материальными точками, имеют массу, равную 1), где |Wf| – мощность множества Wf , т.е.

После формирования очередного w-объекта, все объекты образующего его множества удаляются из исходной обучающей выборки, т.е. X=X\Wf. Алгоритм заканчивает свою работу, когда в исходной обучающей выборке не останется ни одного объекта X=ø.

Построение w-объекта

Рисунок 2 – Построение w-объекта
(анимация: 9 кадров, 5 циклов повторения, 22,1 килобайт)

Принцип формирования образующих множеств, выбирающий близкорасположенные в пространстве признаков объекты, является эффективным способом деления выборки на группы. Введение весов позволяет не только сохранять информацию о количестве заменяемых объектов, но и характеризовать область, в которой эти объекты расположены. Исходя из этого представляется эффективным использование взвешенных обучающих выборок w-объектов в целом и метода w-baseWTS в частности для решения задачи заполнения пропусков в выборках данных.

6. Исследование и разработка методов заполнения пропусков в данных в ДонНТУ 

Задача заполнения пробелов, решаемая при предобработке исходных данных, рассматривалась в работах:

1. Разработка конечной математической модели динамики метеопараметров и прогнозирование их поведения на ее основе;

2. Разработка ПО для анализа и оптимизации деятельности подписного агентства;

3. Разработка компьютеризированной подсистемы анализа и прогнозирования потребления природного газа в условиях ОАО «Донецкгоргаз».

Отметим, что в этих работах использовались известные методы или программные пакеты для заполнения пробелов в данных. Работ, направленных на разработку новых методов заполнения пробелов в данных, найдено не было.

Выводы

В данной работе была рассмотрена задача заполнения пропусков в эмпирических данных. Выяснены причины появления пропусков в данных и проблемы, возникающие из-за их наличия. Рассмотрена классификация пропусков и особенности заполнения таблицы данных в зависимости от вида пропуска.

Выполнен анализ существующих методов импутирования эмпирических данных, по результатам которого выяснено, что одним из наиболее эффективных видов алгоритмов заполнения пропусков является локальное заполнение, не требующее использования дополнительных вычислительных средств и алгоритмов и при этом обеспечивающее высокую эффективность получаемых решений. На близкой к идее формирования групп объектов при локальном заполнении основана идея формирования образующих множеств при построении взвешенных обучающих выборок w-объектов. Наличие весов в выборках w-объектов позволяет не только сохранять информацию о количестве заменяемых объектов, но и характеризовать область, в которой эти объекты расположены. Исходя из этого, разработку нового метода заполнения пропусков в эмпирических данных планируется выполнять на основе взвешенных обучающих выборок.

Список источников

1. Васильев В.И., Шевченко А.И. Восстановление пропущенных данных в эмпирических таблицах // Искусственный интеллект. – 2003. – № 3. – С. 317 – 324.

2. Литтл Р.Дж.А., Рубин Д.Б. Статистический  анализ данных с пропусками. – М.: Финансы и статистика, 1991. – 430 с.

3. Ефимов А.С. Решение задачи кластеризации методом конкурентного обучения при неполных статистических данных // Вестник Нижегородского университета им. Н.И. Лобачевского. – 2010. – №1. – С. 220 – 225.

4. Снитюк В.Е. Эволюционный метод восстановления пропусков в данных // Сборник трудов VI-й Международной конференции «Интеллектуальный анализ информации», Киев, 2006. – С. 262 – 271.

5. Загоруйко Н.Г. Методы распознавания и их применение. – М.: Сов. радио, 1972. – 208 с.

6. Голядина Н.Э., Осипов Е. Метод «Гусеница»-SSA для анализа временных рядов с пропусками [Электронный ресурс]. – Режим доступа: http://www.gistatgroup.com/gus/mvssa1ru.pdf

7. Злоба Е., Яцкив И. Статистические методы восстановления пропущенных данных // Computer Modelling & New Technologies. – 2002. – Vol. 6. – № 1. – P. 51–61.

8. Круглов В.В., Абраменкова И.В. Методы восстановления пропусков в массивах данных // Программные продукты и системы. – 2005. – № 2. [Электронный ресурс]. – Режим доступа: http://www.swsys.ru/index.php?page=article&id=528

9. Зангиева И. Решение проблемы неполноты данных массовых опросов [Электронный ресурс]. – Режим доступа: http://soc.hse.ru/data/2010/05/03/1216376341/7_1.PDF

10. Загоруйко Н.Г., Елкина В.Н., Тимеркаев В.С. Алгоритм заполнения пропусков в эмпирических таблицах (алгоритм Zet) // Эмпирическое предсказание и распознавание образов. – Новосибирск, 1975. – Вып. 61: Вычислительные системы. – С. 3 – 27.

11. Игнатьев Н.А. О синтезе факторов в искусственных нейронных сетях // Вычислительные технологии. – 2005. – № 3. – Том 10. – С. 32 – 38.

12. Волченко Е.В. Метод построения взвешенных обучающих выборок в открытых системах распознавания // Доклады 14-й Всероссийской конференции «Математические методы распознавания образов (ММРО-14)», Суздаль, 2009. – М.: Макс-Пресс, 2009. – С. 100 – 104.

Важное замечание

При написании данного автореферата магистерская работа еще не завершена. Предположительная дата завершения – 10 декабря 2012 г. Полный текст работы, а также материалы по теме могут быть получены у автора или его руководителя после указанной даты.