ДонНТУ   Портал магістрів

Реферат за темою випускної роботи

Зміст

Вступ

Завдання відновлення пропусків (імпутірованія) в емпіричних таблицях є традиційною в класі задач обробки даних, таких, наприклад, як завдання навчання розпізнаванню образів [1]. Традиційними причинами, що призводять до появи пропусків, є неможливість одержання або обробки даних, спотворення або приховування інформації [2]. Об’єктивними причинами цього є поломки устаткування при вимірі тих чи інших характеристик, втрата або обмеження доступу до інформації та інші [3]. Суб’єктивні причини обумовлені людським фактором при накопиченні та обробці інформації внаслідок впливу психологічних аспектів і особливостей пам’яті або навмисного приховування інформації [4]. Так в промисловому експерименті деякі результати можуть бути відсутні внаслідок поломок обладнання, не пов’язаних з експериментом. При опитуванні громадської думки частина опитуваних, можливо, не надасть переваги одному кандидату перед іншим або не відмовиться від надання даних про свої доходи. В результаті на вхід програм аналізу зібраних даних надходять неповні відомості.

Наявність пропусків у даних, так само як і аналіз тільки повних спостережень (після виключення спостережень з пропусками), може привести до отримання зміщених результатів, і як наслідок до спотворення висновків, які можуть бути зроблені за результатами дослідження, і прийняттю невірних стратегічних рішень [5]. Саме тому завдання відновлення пропусків у даних є одним з пріоритетних напрямів аналізу даних для побудови ефективних інтелектуальних систем.


1. Мета і задачі дослідження

Об’єктом дослідження є завдання відновлення пропусків в емпіричних таблицях даних.

Предметом дослідження – методи заповнення пропусків у даних.

Метою випускної роботи магістра є розробка методу заповнення пропусків у емпіричних даних на основі зважених навчальних вибірок.

В процесі роботи необхідно вирішити наступні завдання:

1) дослідити існуючі алгоритми заповнення пропусків у емпіричних даних, критерії оцінки якості відновлених даних;

2) дослідити методи побудови зважених вибірок;

3) розробити метод заповнення пропусків у даних на основі зважених навчальних вибірок;

4) розробити прототип програмної системи тестування алгоритмів відновлення пропусків в емпіричних таблицях даних;

5) виконати порівняльний аналіз запропонованого алгоритму та відомих алгоритмів вирішення даного завдання.

2. Передбачувана наукова новизна

Науковою новизною даної роботи є розробка методу заповнення пропусків у емпіричних даних на основі зважених навчальних вибірок. Оскільки принцип побудови зважених навчальних вибірок, як і багатьох алгоритмів заповнення прогалин в даних, полягає в усередненні значень ознак обраного локального підмножини даних, передбачається, що на основі зважених вибірок може бути побудований ефективний алгоритм імпутірованія даних.

3. Практичне значення

З проблемою обробки пропусків у масивах даних доводиться стикатися при проведенні різноманітних соціологічних, економічних та статистичних (технічних, медичних, геологічних та ін) досліджень. Відновлення пропусків у даних також використовується в задачах нормалізації часових рядів з пропущеними спостереженнями [6] та пошуку близьких за емпіричними даними об’єктів.

У деяких прикладних задачах кількість рядків таблиці даних, відповідних об’єктів дослідження, в яких є пропущені дані, досягає 40%. Відсутність в системі алгоритму відновлення пропусків у даних призведе до необхідності видалення цих об’єктів і, як наслідок, суттєвого зменшення апріорної інформації і погіршення ефективності роботи системи в цілому.

4. Проблема неповних даних і аналіз методів її вирішення

Нехай вихідні дані представлені у вигляді матриц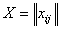і (таблиця 1), рядки якої відповідають l досліджуваних об’єктів, а стовпці є дані по m змінним, вимірювані для кожного об’єкта. елементи матриці , де ,  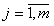є дійсними числами – значеннями безперервних (наприклад, час або розмір доходу), дискретних або категоріальних змінних (наприклад, стать людини). У свою чергу категоріальні ознаки можуть бути впорядкованими (наприклад, освіта) або неупорядкованими (раса, стать).

Причини пропусків даних можуть бути самими різними [7], тому знання механізму, що приводить до відсутності значень, є ключовим при виборі методів аналізу та інтерпретації результатів. Механізм породження перепусток дає розуміння ступеня важливості втраченої інформації, адже неповні дані несуть в собі нову інформацію, необхідну для дослідження, тому їх важливо включати в аналіз.

4.1 Види пропусків у даних

На сьогоднішній день створено значну кількість методів відновлення пропусків, огляд яких міститься, наприклад в [2], однак єдина методологія обробки подібних даних відсутня, незважаючи на її необхідність. Можливість використання методів різного ступеня складності пов’язана з тим, наскільки простим або складним є механізм, згідно з яким дані виявляються пропущеними.

Згідно [2, 8], виділяють наступні види пропусків в даних:

1) повністю випадкові пропуски (data are missing completely at random – MCAR), якщо умовна ймовірність 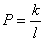, де k – кількість рядків таблиці, що містять пропущене значення, P не залежить ні від самого пропущеного значення змінної, ні від значень інших змінних (ця вірогідність постійна для всіх спостережень);

2) пропуски в даних називаються випадковими (missing at random – MAR), якщо ймовірність P не залежить від самого пропущеного значення змінної, але може залежати від значень інших змінних (у цих випадках механізм пропусків неістотний і до даних застосовується більшість методів відновлення пропусків);

3) пропуски є істотними, якщо ймовірність P залежить від самого пропущеного значення змінної (механізм пропусків є істотним і для коректного аналізу даних необхідно знати цей механізм).

Введені поняття відносяться до окремих змінних, і в межах однієї і тієї ж таблиці даних можна спостерігати всі наведені види пропусків в даних. Необхідно відзначити, що визначення виду пропусків часто не представляється можливим.

4.2 Види алгоритмів імпутірованія даних

Існують два підходи до вирішення проблеми неповних даних.

Перший підхід полягає у виключенні рядків, що містять пропущені дані. Даний метод легко реалізуєм, але необхідною умовою його застосування є дотримання даних вимозі MCAR, тобто пропуски в даних по змінним повинні бути повністю випадковими. Крім того, він зазвичай застосовується лише при незначній кількості пропусків у таблиці, інакше отримана на виході таблиця даних стає непредставительною. Головний недолік такого підходу обумовлений втратою інформації при виключенні неповних даних.

Другий підхід полягає в заповненні пропусків на основі аналізу наявних емпіричних даних. Класифікація методів імпутірованія даних [9] наведена на малюнку 1. Далі наведемо їх опис та особливості використання.

Класифікація методів імпутірованія даних


Малюнок 1 – Класифікація методів імпутірованія даних

1. Заповнення пропусків значеннями змінних таблиці даних. Значення змінної розраховується по всій таблиці або по виділеній локальній групі. Найбільш часто використовують такі алгоритми даного типу [2, 7]:

- заповнення середніми – розраховується по присутніх значеннях змінної по всій таблиці;

- заповнення з упередженим підбором – пропуски заповнюються значеннями, отриманими для іншого подібного об’єкта вибірки (підстановка вибирається для кожного пропущеного значення за оцінкою розподілу);

- підстановка з підбором всередині груп – формуються групи і пропуски в кожній групі заповнюються присутніми значеннями з неї;

- підбір найближчого сусіда (метод Hot Desk) – по заданій метриці визначається найближчий до заповнюваних об’єкт по всім присутнім значенням змінних, і пропуск заповнюється значенням відповідної змінної найближчого об’єкта;

- заповнення по регресії – по комплектним даними будується рівняння лінійної множинної регресії і обчислюються пропущені значення змінної. При використанні методу багатовимірної регресії будується модель лінійної залежності змінної, в якій необхідно заповнити пропуски, від ряду інших наявних ознак. Регресійні коефіцієнти для кожного з предикторів знаходяться методом найменших квадратів в масиві з повними даними. Підставляючи значення предикторів в регресійне рівняння, отримують прогноз пропущеного показника;

- заповнення значенням змінної випадково вибраного об’єкту;

- багаторазове заповнення з підбором значення змінної за заданими критеріями;

- складові методи.

2. Заповнення пропусків на основі моделювання. Виконується побудова моделі породження пропусків. Висновки отримують за допомогою функції правдоподібності, побудованої за умови справедливості цієї моделі, з оцінюванням параметрів методами типу максимальної правдоподібності.

Найбільш ефективним методом моделювання є ЕМ-алгоритм [2, 9]. Метод максимізації очікувань (ЕМ – expectation maximization), в деяких джерелах так само званий ЕМ – оцінюванням, є ітераційною процедурою, призначеною для вирішення завдань оптимізації деякого функціоналу, через аналітичний пошук екстремуму цільової функції.

На першому етапі Е (expectation) за сукупністю наявних абсолютно повних або частково (за цільовою змінної) повних спостережень розраховуються умовні очікувані значення цільової змінної для кожного неповного спостереження. Потім після отримання масиву повних спостережень, оцінюються основні статистичні параметри: заходи середньої тенденції і розкиду, показники взаємної кореляції і коваріації змінних. У разі роботи з неповними данимі на Е – етапі визначається функція умовного математичного очікування логарифма повної функції правдоподібності при відомому значенні цільової змінної Х.

На другому етапі М (maximization), завдання алгоритму максимізувати ступінь взаємної відповідності очікуваних і реально підставляється даних, а також відповідності структури імпутірованих даних структурі даних повних спостережень.

3. Resampling метод [4, 7]. Метод Resampling грунтується на бутстреп-підході, який передбачає багаторазову обробку різних частин одних і тих же даних і зіставлення отриманих таким чином результатів.

Суть алгоритму Resampling полягає в тому, що значення для перепусток вибираються з наявних випадковим чином, з поверненням (коли значення може використовуватися ще раз після вибору) або без нього. Після цього на всьому масиві будується регресійна модель, що дозволяє передбачити значення для прогалин. Для всіх передбачуваних предикторів знаходяться регресійні коефіцієнти і константа. Потім обчислюються підсумкові значення регресійних коефіцієнтів, за якими і будуть передбачені остаточні пропущені значення.

Перевагою даного методу є повторне використання вихідних даних, адже збільшення числа підвибірок дозволяє найбільш повно використовувати вихідну інформацію. З іншого боку, обсяг нової інформації зменшується для кожної нової підвибірки, оскільки збільшується вірогідність того, що дані елементи вибірки були вже вибрані раніше, – це основний недолік методу вкупі з відсутністю процедур його оптимізації.

4. Локальні алгоритми відновлення пропусків (алгоритми Zet і ZetBraid) [5, 10]. Алгоритми сімейства Zet (Wanga) і ZetBraid, по суті, є детально відпрацьованою і апробованою технологією верифікації експериментальних даних, заснованою на гіпотезі їх надмірності. Зовні вони схожі з методом локального заповнення.

Суть алгоритму Zet полягає в підборі для кожного пропуску імпутіруемого значення не з усієї сукупності повних спостережень, а з деякої її частини, званої компонентною матрицею. Вона складається з компонентних рядків і стовпців. Компонентність деяких рядків або об’єктів являє собою величину зворотньопропорційну декартовомій відстані до цільовою рядка (неповного спостереження з пропуском) в просторі, осі якого задані змінними – розглянутими характеристиками об’єктів.

За даними компонентної матриці потім будується функціональна залежність прогнозованого значення від відповідного значення в компетентній матриці, на основі якої, потім, прогнозується значення пропуску.

Основна відмінність і одночасно перевага алгоритму ZetBraid (плетіння) від алгоритму Zet полягає в тому, що в ньому закладено апарат для об’єктивного визначення розмірності компонентної матриці. В процесі роботи алгоритму відбувається послідовний почерговий відбір компетентних рядків і компетентних стовпців. При кожному новому відборі рядка або стовпця формується нова компетентна матриця. По заданому критерію визначається її ефективність при прогнозуванні пропусків.

Також існують нейромережеві й еволюційні алгоритми заповнення пропусків у даних [4, 11].

Необхідно також зазначити, що крім очевидних переваг, імпутірованіє, як спосіб вирішення проблеми недостатньої інформації має декілька недоліків, які не можна не враховувати [9]:

1) використання для передбачення пропусків наявних повних даних спотворює структуру результуючих даних (після імпутірованія), яка зміщується в бік структури тільки повних спостережень;

2) штучна підстановка пропусків вносить в масив певну частку штучних даних, які в свою чергу призводять до зміщення значущості одержуваних на їх основі результатів.

Моделі, побудовані за відновленими даними, можуть бути менш точними в порівнянні з ідеальною моделлю, побудованою лише на повних спостереженнях. Втрати в їх точності залежатимуть від якості передбачення відсутніх значень, тобто від вибору алгоритму заповнення пропусків у даних і від обсягу оброблюваних даних.

Одним з найбільш ефективних способів заповнення пропусків у даних є локальне заповнення (заповнення з підбором всередині груп). На ідеї виділення груп засновані і алгоритми побудови зважених навчальних вибірок w-об’єктів.

5. Побудова зважених навчальних вибірок на основі методу w-baseWTS

В роботі [12] запропоновано метод w-baseWTS побудови виваженої навчальної вибірки w-об'єктів для скорочення вибірок великого обсягу. Основою даного методу є вибір множин близько розташованих об’єктів вихідної вибірки та їх заміна одним зваженим об’єктом нової вибірки. Значення ознак кожного об’єкта нової вибірки є центрами мас значень ознак об’єктів вихідної вибірки, які він замінює. Введений додатковий параметр – вага визначається як кількість об’єктів вихідної вибірки, які були замінені одним об’єктом нової вибірки. Запропонований метод орієнтований як на скорочення вихідної навчальної вибірки, так і на аналіз необхідності коригування вибірки і швидке виконання такого коригування при поповненні вибірки в процесі роботи системи.

Побудова w-об’єкта складається з трьох послідовних етапів:

1) побудова утворює безліч Wf , яка містить деяку кількість d об’єктів вихідної вибірки, що належать одному класу;

2) формування вектора XiW={xi1, xi2, …, xin} значень ознак w-об’єкта XiWі розрахунок його ваги pi;

3) коректування вихідної навчальної вибірки – видалення об’єктів, включених в утворювану безліч X=X\Wf.

Побудова утворюваної безлічі Wf полягає в знаходженні початкової точки Xf1 формування w-об’єкта, визначенні конкуруючої точки Xf2 і виборі в утворюваній безлічі Wf таких об’єктів вихідної вибірки, відстань до кожного з яких від початкової точки менше, ніж відстань від них до конкуруючої точки. В якості початкової точки Xf1 формування w-об’єкта використовується об’єкт вихідної навчальної вибірки, найбільш віддалений від усіх об’єктів інших класів. Конкуруюча точка Xf2 вибирається шляхом знаходження найближчого до  Xf1 об’єкта, що не належить того ж класу, що і сам  Xf1,  тобто  yf1≠yf2.

Вибір об’єктів {Xf1, Xf2, …, Xd} утворюваної безлічі Wf здійснюється за наступним правилом: об’єкт Xi включається в Wf, якщо: 

1) він належить тому ж класу, що і початкова точка Xf1;

2) відстань від даного об’єкту до початкової точки Xf1  менше, ніж до конкуруючої точки Xf2;

3) відстань Ri1 от рассматриваемого объекта до начальной точки меньше расстояния  Ri2 від даного об’єкту до початкової точки менше відстані R12 між початковою і конкуруючої точками (для випадку, коли класи складаються з декількох окремих областей ознакового простору).

Таким чином, утворювана безліч Wf формується за правилом:

Принцип формування утворюваної безлічі наведено на малюнку 2.

Значення ознак {xi1, xi2, …, xin} нового w-об’єкту XiWформуються по утворюваній безлічі Wf і розраховуються як координати центру мас системи з pf=|Wf| матеріальних точок (приймемо, що об’єкти вихідної навчальної вибірки, які є в просторі ознак матеріальними точками, мають масу, рівну 1), де |Wf| – потужність безлічі Wf , тобто

Після формування чергового w-об’єкта, всі об’єкти утворюваної його безлічі видаляються з вихідної навчальної вибірки, тобто X=X\Wf. Алгоритм закінчує свою роботу, коли у вихідній навчальній вибірці не залишиться жодного об’єкту X=ø.

Побудова w-об’єкта

Малюнок 2 – Побудова w-об’єкта
(анімація: 9 кадрів, 5 циклів повторення, 22,1 кілобайт)

Принцип формування утворюваних безлічей, що вибирає близько розташованих в просторі ознак об’єкти, є ефективним способом розподілу вибірки на групи. Введення ваг дозволяє не тільки зберігати інформацію про кількість замінних об’єктів, а й характеризувати область, в якій ці об’єкти розташовані. Виходячи з цього представляється ефективним використання зважених навчальних вибірок w-об’єктів в цілому і методу w-baseWTS зокрема для вирішення задачі заповнення пропусків у вибірках даних.

6. Дослідження і розробка методів заповнення пропусків у даних в ДонНТУ

Завдання заповнення пропусків, яке вирішується при передобробці вихідних даних, розглядалася в роботах:

1. Розробка кінцевої математичної моделі динаміки метеопараметрів і прогнозування їх поведінки на її основі;

2. Разработка ПО для анализа и оптимизации деятельности подписного агентства;

3. Разработка компьютеризированной подсистемы анализа и прогнозирования потребления природного газа в условиях ОАО «Донецкгоргаз».

Відзначимо, що в цих роботах використовувалися відомі методи чи програмні пакети для заповнення пропусків в даних. Робіт, спрямованих на розробку нових методів заповнення пропусків в даних, знайдено не було.

Висновки

У даній роботі була розглянута задача заповнення пропусків у емпіричних даних. З’ясовано причини появи пропусків в даних і проблеми, що виникають через їх наявності. Розглянута класифікація пропусків і особливості заповнення таблиці даних в залежності від виду пропуску.

Виконано аналіз існуючих методів імпутірованія емпіричних даних, за результатами якого з’ясовано, що одним з найбільш ефективних видів алгоритмів заповнення пропусків є локальне заповнення, що не вимагає використання додаткових обчислювальних засобів і алгоритмів і при цьому забезпечує високу ефективність одержуваних рішень. На близькій до ідеї формування груп об’єктів при локальному заповненні заснована ідея формування утворюють множин при побудові зважених навчальних вибірок w-об’єктів. Наявність ваг на вибірках w-об’єктів дозволяє не тільки зберігати інформацію про кількість замінних об’єктів, а й характеризувати область, в якій ці об’єкти розташовані. Виходячи з цього, розробку нового методу заповнення пропусків у емпіричних даних планується виконувати на основі зважених навчальних вибірок.

Перелік посилань

1. Васильев В.И., Шевченко А.И. Восстановление пропущенных данных в эмпирических таблицах // Искусственный интеллект. – 2003. – № 3. – С. 317 – 324.

2. Литтл Р.Дж.А., Рубин Д.Б. Статистический  анализ данных с пропусками. – М.: Финансы и статистика, 1991. – 430 с.

3. Ефимов А.С. Решение задачи кластеризации методом конкурентного обучения при неполных статистических данных // Вестник Нижегородского университета им. Н.И. Лобачевского. – 2010. – №1. – С. 220 – 225.

4. Снитюк В.Е. Эволюционный метод восстановления пропусков в данных // Сборник трудов VI-й Международной конференции «Интеллектуальный анализ информации», Киев, 2006. – С. 262 – 271.

5. Загоруйко Н.Г. Методы распознавания и их применение. – М.: Сов. радио, 1972. – 208 с.

6. Голядина Н.Э., Осипов Е. Метод «Гусеница»-SSA для анализа временных рядов с пропусками [Электронный ресурс]. – Режим доступа: http://www.gistatgroup.com/gus/mvssa1ru.pdf

7. Злоба Е., Яцкив И. Статистические методы восстановления пропущенных данных // Computer Modelling & New Technologies. – 2002. – Vol. 6. – № 1. – P. 51–61.

8. Круглов В.В., Абраменкова И.В. Методы восстановления пропусков в массивах данных // Программные продукты и системы. – 2005. – № 2. [Электронный ресурс]. – Режим доступа: http://www.swsys.ru/index.php?page=article&id=528

9. Зангиева И. Решение проблемы неполноты данных массовых опросов [Электронный ресурс]. – Режим доступа: http://soc.hse.ru/data/2010/05/03/1216376341/7_1.PDF

10. Загоруйко Н.Г., Елкина В.Н., Тимеркаев В.С. Алгоритм заполнения пропусков в эмпирических таблицах (алгоритм Zet) // Эмпирическое предсказание и распознавание образов. – Новосибирск, 1975. – Вып. 61: Вычислительные системы. – С. 3 – 27.

11. Игнатьев Н.А. О синтезе факторов в искусственных нейронных сетях // Вычислительные технологии. – 2005. – № 3. – Том 10. – С. 32 – 38.

12. Волченко Е.В. Метод построения взвешенных обучающих выборок в открытых системах распознавания // Доклады 14-й Всероссийской конференции «Математические методы распознавания образов (ММРО-14)», Суздаль, 2009. – М.: Макс-Пресс, 2009. – С. 100 – 104.

Важливе зауваження

При написанні даного автореферату магістерська робота ще не завершена. Можлива дата завершення – 10 грудня 2012. Повний текст роботи, а також матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.