Реферат по теме выпускной работы
Содержание
- Введение
- 1. Актуальность темы
- 2. Цель и задачи исследования
- 3. Способы и средства снижения динамических нагрузок подсистемы привода исполнительных органов комбайна КДК500
- 4. Исследование динамических процессов блока привода исполнительного органа
- Выводы
- Список источников
Введение
Повышение производительности и снижение удельных энергозатрат при добыче полезного ископаемого являются основными задачами ведения выемочных работ. Необходимым условием рентабельности угольного предприятия состоит в необходимости повышения объемов добычи угля и снижение его себестоимости.
Усложняющиеся условия эксплуатации требуют разработки все более современных машин. Этого можно достичь улучшая технико-экономические показатели использования машин за счет обоснованного выбора их параметров. Обоснованное изменение некоторых параметров машин позволяет существенно повысить их производительность без существенных конструкторских доработок [2].
В связи с этим актуальным и необходимым есть выбор рациональных режимных параметров используемых очистных машин с целью повышения эффективности их эксплуатации, что в результате приводит к повышению производительности всего комплекса оборудования. Совершенствование конструктивных недостатков комбайнов, выявленных в процессе их эксплуатации, ведет к повышению надежности очистных машин и снижению времени их простоев.
Также стоит вопрос снижения нагрузок силовых подсистем на основе оптимизации динамических свойств комбайнов при разрушении угольных пластов сложной структуры и неравномерности перемещения их вдоль забоя.
Таким образом, обоснование параметров очистного комбайна является актуальной научной задачей и областью рассмотрения широкого спектра вопросов.
1. Актуальность темы
Важную роль в современной угольной промышленности играет повышение конкурентоспособности изделий горного машиностроения на основе повышения их технического уровня. Как показывает опыт передовых отраслей машиностроения, одним из путей решения этой задачи является широкое внедрение методов математического моделирования рабочих процессов и оптимизации структуры и параметров на всех этапах создания новой техники от проектирования до доведения серийно-выпускаемых машин [1].
Для очистных комбайнов актуальна задача повышения ресурса до уровня, соответствующего лучшим мировым образцам. Решение поставленных задач требует повышения качества и сокращения сроков проектирования, а также освоения новой техники [2].
В исследовании и создании машин методы математического моделирования рабочих процессов являются основой САПР, однако еще не находят широкого применения. Одной из причин недоработок - это отсутствие общей концепции математического моделирования рабочих процессов ПРМ, а также недостаточное изучение закономерностей формирования нагрузок во взаимодействующих подсистемах машин как нелинейных автономных стохастических систем.
2. Цель и задачи исследования
Целью данной магистерской работы является повышение технического уровня привода исполнительного органа очистного комбайна за счёт разработки и реализации имитационной математической модели их рабочего процесса. Модель позволяет установить закономерности и обосновать рациональные структуры и параметры. Для достижения поставленной задачи были сформулированы и решены следующие задачи:
- Разработана математическая модель функционирования привода исполнительного органа, описывающая процессы формирования динамических нагрузок.
- Разработана методика и программное обеспечение на этапе отладки для проведения вычислительных экспериментов.
- Установлены закономерности формирования динамических нагрузок в установившихся и переходных режимах работы.
- Исследованы возможные структуры и параметры привода и установлены наиболее рациональные из них, позволяющие снизить уровень нагрузок в различных режимах работы.
3. Способы и средства снижения динамических нагрузок подсистемы привода исполнительных органов комбайна КДК500
При работе очистного комбайна его силовые системы подвергаются внешним и внутренним воздействиям.
Внешние возмущающие воздействия на входах систем комбайна (исполнительных органах, устройствах для погрузки и транспортировки отбитого угля и породы, опорах комбайна, со стороны питающей сети) носят стохастический характер.
К числу внутренних возмущений в силовых системах следует отнести возмущения от зубчатых соединительных муфт, зубчатых передач, возмущения со стороны электродвигателей, гидравлических машин (насосов, двигателей).
Взаимодействие вышеуказанных силовых динамических систем носит весьма сложный характер и обусловлено внешними и внутренними связями.
Внешние связи проявляются в воздействии на процесс формирования внешних возмущений колебательных процессов во взаимодействующих системах машин, а внутренне - обусловлены динамическими свойствами, связанностью этих систем.
Реализация высоких значений устойчивых моментов привода при повышенных параметрах разрушения горного массива исполнительными органами современны комбайнов, оснащённых достаточно надёжными регуляторами нагрузки, как известно, приводит к высокой динамической нагруженности силовых систем машин и, в первую очередь, систем приводов исполнительных органов. В результате снижаются надёжность и долговечность комбайнов, а следовательно, и их производительность.
Рассмотрим формирование динамических нагрузок в системах приводов на примере широко распространённых угледобывающих комбайнов со шнековыми органами.
При установившихся рабочих режимах в спектральном составе нагрузок систем приводов современных шнековых комбайнов наряду со случайными составляющими существенна доля низкочастотных и высокочастотных колебательны составляющих.
Низкочастотные колебания (1-3 Гц) в значительной степени обусловлены особенностями формирования момента сил сопротивления на шнековых исполнительных органах, движение осей вращения которых, характеризуется существенной неравномерностью в направлении перемещения комбайна и направлении, перпендикулярном плоскости пласта.
Высокочастотные колебательные составляющие с корреляционными функциями вида
∑Di*e^-α1i(τ)*cosω1iτ/∑D2j*cosω2jτ характеризуется частотами (8-50 Гц), практически совпадающими с расчётными значениями собственных частот крутильных колебаний системы привода и обусловлены сложными автоколебательными процессами в автономной системе «комбайн-забой».
Для того, чтобы более чётко предоставить закономерности формирования динамических нагрузок в системах приводов, представляется методически целесообразным рассматривать эти колебательные процессы условно состоящими из первичных и вторичных колебаний.
Первичные высокочастотные составляющие обусловлены стохастическим характером нагрузки на резцы исполнительного органа. При этом флуктуационные всплески сил сопротивления, выполняющие роль клапана автоколебательной системы, закручивают рассматриваемую систему на определённую величину угловой деформации, после чего происходит скол части массива. Обратная связь с колебательной системой состоит в том, что упругие и инерционные свойства обусловливают дальнейшее колебательное движение системы.
При этом автоколебания в общем случае относятся к стохастическим и для слабодемпфированных систем, к которым следует отнести системы приводов горных комбайнов, могут рассматриваться как свободно-сопровождающие колебания со случайными уровнем и частотой возмущения.
Первичные низкочастотные составляющие обусловлены колебаниями момента сил сопротивления вследствие нерационального размещения режущего инструмента на дополнительных органах и зависят от конструктивных особенностей шнеков [4].
4. Исследование динамических процессов блока привода исполнительного органа
На современном этапе развития горного дела целесообразно применение лучших серийных очистных комбайнов с повышенными показателями надежности и адаптивности. Одним из основных способов повышения надежности ОК является снижение их динамической нагруженности. А также электромеханической подсистемы привода исполнительных органов. Чтобы выявить закономерности формирования динамической нагруженности в подсистемы привода исполнительных органов наряду с экспериментальными методами применяется имитационное математическое моделирование [8],[11].
В данной магистерской работе рассматривается привод исполнительного органа КДК500, изображенный на рис.1.
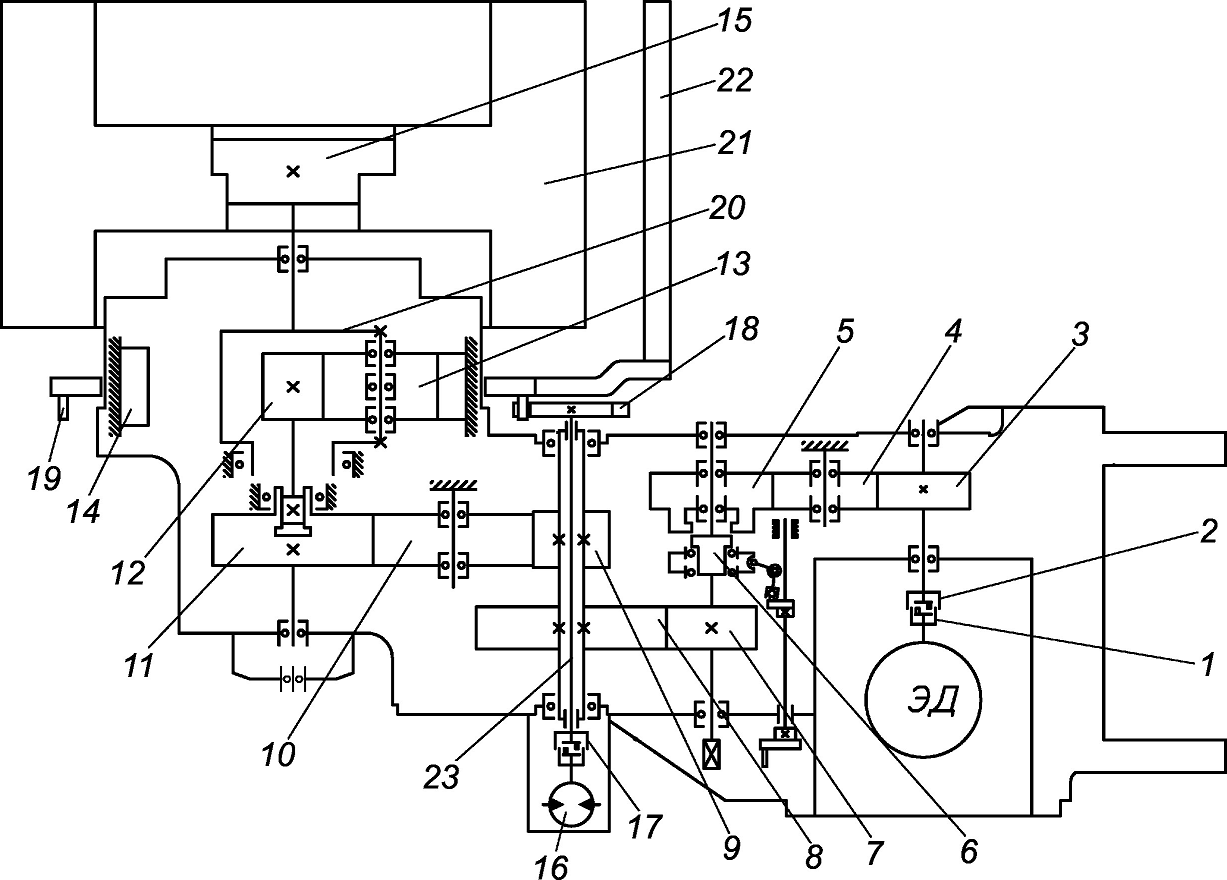
Рис.1 – Кинематическая схема блока привода исполнительного органа КДК500
Для проведения исследований динамических процессов блока привода исполнительного органа, разработана упрощённая математическая модель привода, учитывающая кинематические составляющие нагрузки. Эта модель позволила получить предварительные данные о формировании кинематических нагрузок в приводе.
Для решения поставленной задачи - разработке математической модели привода исполнительного органа КДК500, были приняты такие допущения:
- что все элементы схемы сводятся к системе с сосредоточенными дискретными массами ротора электродвигателя с присоединенными массами редуктора и исполнительного органа с присоединенными массами выходного вала;
- упругие и диссипативные свойства привода приняты линейными и характеризуются коэффициентами жесткости с и сопротивления β;
- изгибные деформации вала, радиальные деформации их опор – подшипниковых узлов – приняты в виде линейных функций результирующего вектора радиальной нагрузки, действующей на ИО, и характеризуются коэффициентами жесткости С и сопротивления β;
- между крутильными и поперечными колебаниями ИО отсутствует внутренняя динамическая связь.
Эквивалентная расчетная схема для составления математической модели представлена на анимации:
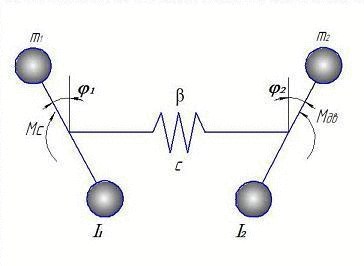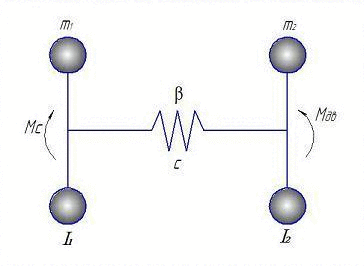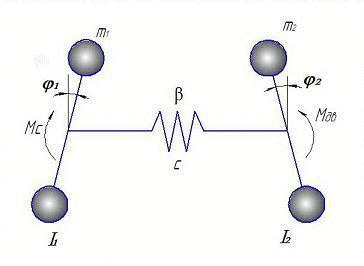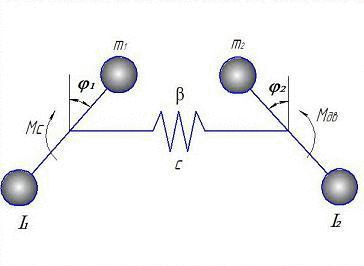
Рисунок 2 – Расчетная двухмассовая модель (Анимация сделана с помощью GIF Animator. Состоит из 6 кадров с интервалом в 500 мс.)
На представленной расчетной двухмассовой системе, I1 - это моменты инерции ротора электродвигателя, I2 – исполнительного органа, с - коэффициент жесткости и β - коэффициент сопротивления.
За обобщенные координаты приняты φ1, φ2, – углы поворота соответственно ротора электродвигателя и исполнительного органа, соответствующие массам с моментами инерции I1 … I2, а также электромагнитный момент двигателя Мд. Все параметры расчётной динамической схемы приведены к валу ИО [6],[11].
Составленная математическая модель привода исполнительного органа была осуществлена с использованием фундаментальных уравнений Парка-Горева, а также с использование уравнений Лагранжа II рода, в результате чего получена следующая система нелинейных дифференциальных уравнений:
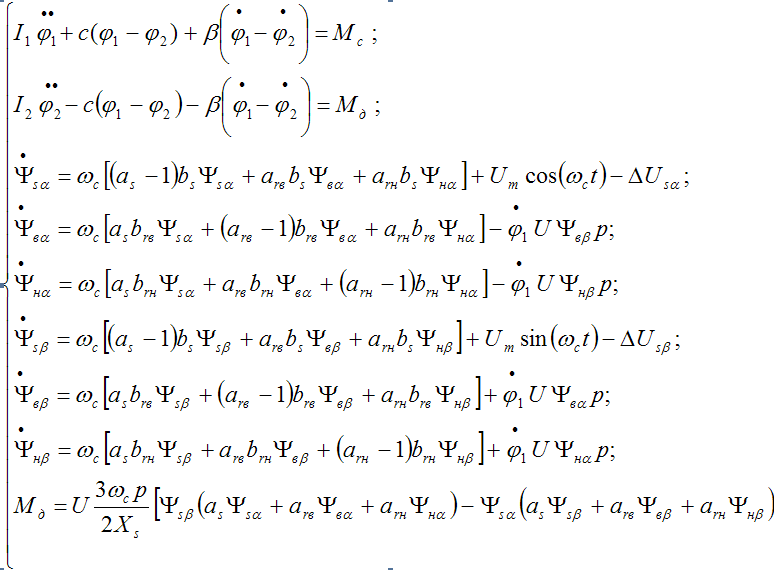
Первые два уравнения системы описывают движение инерционных масс привода исполнительного органа, следующие семь – динамические процессы, протекающие в асинхронном электродвигателе [2],[3].
Для описания динамики асинхронного электродвигателя в качестве обобщённых координат используются потокосцепления статора и ротора ψsα, ψвα, ψнα, ψвβ, ψнβ, ψsβ.
В основу алгоритма и программы моделирования динамических составляющих нагрузки положен метод Рунге-Кутта четвёртого порядка, который был использован для решения СДУ, с постоянным шагом интегрирования. Выбранный метод является наиболее распространенным для решения подобных систем благодаря высокой точности, меньшей склонности к возникновению неустойчивости решения по сравнению с другими численными методами [8].
Разработанная программа позволяет исследовать динамические процессы в приводе исполнительного органа в различных режимах работы, проводить оптимизационные вычислительные эксперименты и получать исходные данные для выполнения прочностных расчётов трансмиссии.
Выводы
Основные выводы, научные и практические результаты состоят в следующем:
- Разработана комплексная имитационная модель функционирования, включающая в себя:
- математическую модель формирования нагрузок на исполнительном органе по результатам моделирования;
- математическую модель динамики, учитывающую нелинейные связи, обусловленные наличием асинхронного электродвигателя, упругой пальцевой муфты и предохранительных устройств (динамика асинхронного электродвигателя описана уравнениями Парка-Горева).
Комплексная имитационная модель адекватно описывает рабочий процесс, наряду с нелинейностью динамических свойств привода и стохастичностью рабочего процесса, учитывает переходные динамические процессы в асинхронном электродвигателе и позволяет моделировать её работу в следующих режимах: запуск вхолостую, запуск под завалом, номинальный режим функционирования.
- С использованием разработанного математического и программного обеспечения, а также методики проведения вычислительных исследований и оптимизационных экспериментов получены и обоснованы оптимальные структура и параметры привода исполнительного органа.
При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2013 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Список источников
- Сивокобыленко В.Ф., Костенко В.И. Математическое моделирование динамических режимов двухдвигательного асинхронного электропривода // Извести вузов. Энергетика.– Минск, 1974. – № 1. – с. 43-48.
- Гуляев В.Г., Сивокобыленко В.Ф., Жуков К.В. Математическая модель двухдвигательного привода исполнительных органов очистного комбайна // Труды Донецкого государственного технического университета. Выпуск 7, серия горно-электромеханическая. ДонГТУ. – Донецк, – 1999. – с. 97-102.
- Пинчук И.С. Переходные процессы в асинхронных электродвигателях при периодической нагрузке // Электричество. – 1957. – № 9. – с. 27-30.
- Гуляев В.Г. Проектирование и конструирование горных машин и комплексов. Часть 1. Выемочные комбайны //ГВУЗ "ДонНТУ", Технопарк ДонНТУ "УНИТЕХ", 2011.- 322с.
- Малеев Г.В., Гуляев В.Г., Бойко Н.Г., Горбатов П.А., Межаков В.А. Проектирование и конструирование горных машин и комплексов. – М.: Недра, 1988. – 368 с.
- Тарасенко В.А. Проведение вычислительных экспериментов с использованием сложных имитационных моделей горных машин // XXI столетие – проблемы и перспективы освоения месторождений полезных ископаемых: Сб. науч. трудов НГА Украины. № 3, Том 6. Горные машины и комплексы. – Днепропетровск: РИК НГА Украины, – 1998. – с. 71-75.
- Докукин А.В., Красников Ю.Д., Хургин З.Я. и др. Динамические процессы горных машин.– М.: Наука, 1972. – 150 с.
- Кондрахин В.П., Гуляев В.Г., Головин В.Л. Имитационная математическая модель динамических процессов очистных комбайнов высокой энерговооруженности с вынесенной системой подачи / Наукові праці донецького національного технічного університету. Випуск 12 (113). Серія гірничо-електромеханічна. Донецьк,2006.- с. 123-130.
- Нечепуренко М.С. Обоснование параметров и разработка узлов горных машин с упругим преобразователем движений.– Автореф. дисс… канд. техн. наук: 05.05.06 –Донецк, 1987. – 18 с.
- Докукин А.В. Оптимизация привода выемочных и проходческих машин. – М.: Недра, 1983. – 264 с.
- Тарасенко В.А. Моделирование рабочих процессов и обоснование параметров шахтной одновалковой дробилки для крепких пород. Диссертация на соискание учёной степени кандидата технических наук по специальности – ДонНТУ, Донецк, 2000.
