Реферат за темою випускної роботи
Зміст
- Вступ
- 1. Актуальність теми
- 2. Мета і задачі дослідження
- 3. Способи та засоби зниження динамічних навантажень підсистеми приводу виконавчих органів комбайна КДК500
- 4. Дослідження динамічних процесів блоку приводу виконавчого органу
- Висновки
- Перелік посилань
Вступ
Підвищення продуктивності і зниження удільних енерговитрат при здобичі корисної копалини є основними завданнями ведення очисних робіт. Необхідною умовою рентабельності вугільного підприємства полягає в необхідності підвищення об'ємів видобутку вугілля і зниження його собівартості.
Умови експлуатації, дедалі складніші, вимагають розробки все більш сучасних машин. Цього можна досягти покращуючи техніко-економічні показники використання машин за рахунок обгрунтованого вибору їх параметрів. Обгрунтована зміна деяких параметрів машин дозволяє значно підвищити їх продуктивність без суттєвих конструкторських доопрацювань [2].
У зв'язку з цим актуальним і необхідним є вибір раціональних режимних параметрів використовуваних очисних машин з метою підвищення ефективності їх експлуатації, що в результаті призводить до підвищення продуктивності усього комплексу устаткування. Вдосконалення конструктивних недоліків комбайнів, виявлених в процесі їх експлуатації, веде до підвищення надійності очисних машин і зниження часу їх простоїв.
Також стоїть питання зниження навантажень силових підсистем на основі оптимізації динамічних властивостей комбайнів при руйнуванні вугільних пластів складної структури і нерівномірності переміщення їх уздовж забою.
Таким чином, обгрунтування параметрів очисного комбайна є актуальним науковим завданням і областю розгляду широкого спектру питань.
1. Актуальність теми
Важливу роль в сучасній вугільній промисловості грає підвищення конкурентоспроможності виробів гірничого машинобудування на основі підвищення їх технічного рівня. Як показує досвід передових галузей машинобудування, одним з шляхів рішення цієї задачі є широке впровадження методів математичного моделювання робочих процесів і оптимізації структури і параметрів на усіх етапах створення нової техніки від проектування до доведення машин, що серійно випускаються.
Для очисних комбайнів актуальне завдання підвищення ресурсу до рівня, що відповідає кращим світовим зразкам. Рішення поставлених завдань вимагає підвищення якості і скорочення термінів проектування, а також освоєння нової техніки.
У дослідженні і створенні машин методи математичного моделювання робочих процесів є основою САПР, проте ще не знаходять широкого застосування. Однією з причин недоробок - це відсутність загальної концепції математичного моделювання робочих процесів ПРМ, а також недостатнє вивчення закономірностей формування навантажень у взаємодіючих підсистемах машин як нелінійних автономних стохастичних систем.
2. Мета і задачі дослідження
Метою цієї магістерської роботи є підвищення технічного рівня приводу виконавчого органу очисного комбайну за рахунок розробки і реалізації імітаційної математичної моделі їх робочого процесу. Модель дозволяє встановити закономірності і обгрунтувати раціональні структури і параметри. Для досягнення поставленого завдання були сформульовані і вирішені наступні завдання:
- Розроблена математична модель функціонування приводу виконавчого органу, що описує процеси формування динамічних навантажень.
- Розроблена методика і програмне забезпечення на етапі відлаштування для проведення обчислювальних експериментів.
- Встановлені закономірності формування динамічних навантажень в сталих і перехідних режимах роботи.
- Досліджені можливі структури і параметри приводу і встановлені найбільш раціональні з них, дозволяють понизити рівень навантажень в різних режимах роботи.
3. Способи та засоби зниження динамічних навантажень підсистеми приводу виконавчих органів комбайна КДК500
При роботі очисного комбайна його силові системи піддаються зовнішнім і внутрішнім впливам.
Зовнішні впливи на входах систем комбайна (виконавчих органах, пристроях для вантаження і транспортування відбитого вугілля і породи, опорах комбайна, з боку живильної мережі) носять стохастичний характер.
До числа внутрішніх збурень у силових системах слід віднести обурення від зубчастих з'єднувальних муфт, зубчастих передач, обурення з боку електродвигунів, гідравлічних машин (насосів, двигунів).
Взаємодія вищевказаних силових динамічних систем носить досить складний характер і обумовлено зовнішніми і внутрішніми зв'язками.
Зовнішні зв'язки проявляються у впливі на процес формування зовнішніх збурень коливальних процесів у взаємодіючих системах машин, а внутрішньо - обумовлені динамічними властивостями, пов'язаністю цих систем.
Реалізація високих значень стійких моментів приводу при підвищених параметрах руйнування гірського масиву виконавчими органами сучасні комбайнів, оснащених досить надійними регуляторами навантаження, як відомо, призводить до високої динамічної навантаженості силових систем машин і, в першу чергу, систем приводів виконавчих органів. В результаті знижуються надійність і довговічність комбайнів, а отже, і їх продуктивність.
Розглянемо формування динамічних навантажень у системах приводів на прикладі широко поширених вугледобувних комбайнів зі шнековими органами.
При сталих робочих режимах в спектральному складі навантажень систем приводів сучасних шнекових комбайнів поряд з випадковими складовими істотна частка низькочастотних і високочастотних коливальних складових.
Низькочастотні коливання (1-3 Гц) значною мірою зумовлені особливостями формування моменту сил опору на шнекових виконавчих органах, рух осей обертання яких, характеризується істотною нерівномірністю в напрямку переміщення комбайна і напрямку, перпендикулярному площині пласта.
Високочастотні коливальні складові з кореляційними функціями виду
∑Di*e^-α1i(τ)*cosω1iτ/∑D2j*cosω2jτ характеризується частотами (8-50 Гц), практично збігаються з розрахунковими значеннями власних частот крутильних коливань системи приводу і обумовлені складними автоколивальними процесами в автономній системі комбайн-вибій
.
Для того, щоб більш чітко надати закономірності формування динамічних навантажень у системах приводів, представляється методично доцільне розглядати ці коливальні процеси умовно складаються з первинних і вторинних коливань.
Первинні високочастотні складові обумовлені стохастичним характером навантаження на різці виконавчого органу. При цьому флуктуаційні сплески сил опору, що виконують роль клапана автоколебательной системи, закручують розглянуту систему на певну величину кутової деформації, після чого відбувається відкол частини масиву. Зворотний зв'язок з коливальної системою полягає в тому, що пружні і інерційні властивості обумовлюють подальше коливальний рух системи.
При цьому автоколивання в загальному випадку відносяться до стохастичним і для слабодемпфірованних систем, до яких слід віднести системи приводів гірничих комбайнів, можуть розглядатися як вільно-супроводжуючі коливання з випадковими рівнем і частотою обурення.
Первинні низькочастотні складові обумовлені коливаннями моменту сил опору внаслідок нераціонального розміщення ріжучого інструменту на додаткових органах і залежать від конструктивних особливостей шнеків [4].
4. Дослідження динамічних процесів блоку приводу виконавчого органу
На сучасному етапі розвитку гірничого діла доцільне застосування кращих серійних очисних комбайнів з підвищеними показниками надійності і адаптивності. Одним з основних способів підвищення надійності ОК є зниження їх динамічної навантаженості. А також електромеханічної підсистеми приводу виконавчих органів. Щоб виявити закономірності формування динамічної навантаженості в підсистемі приводу виконавчих органів разом з експериментальними методами застосовується імітаційне математичне моделювання [8],[11].
У цій магістерській роботі розглядається привід виконавчого органу КДК500, зображений на рис.1.
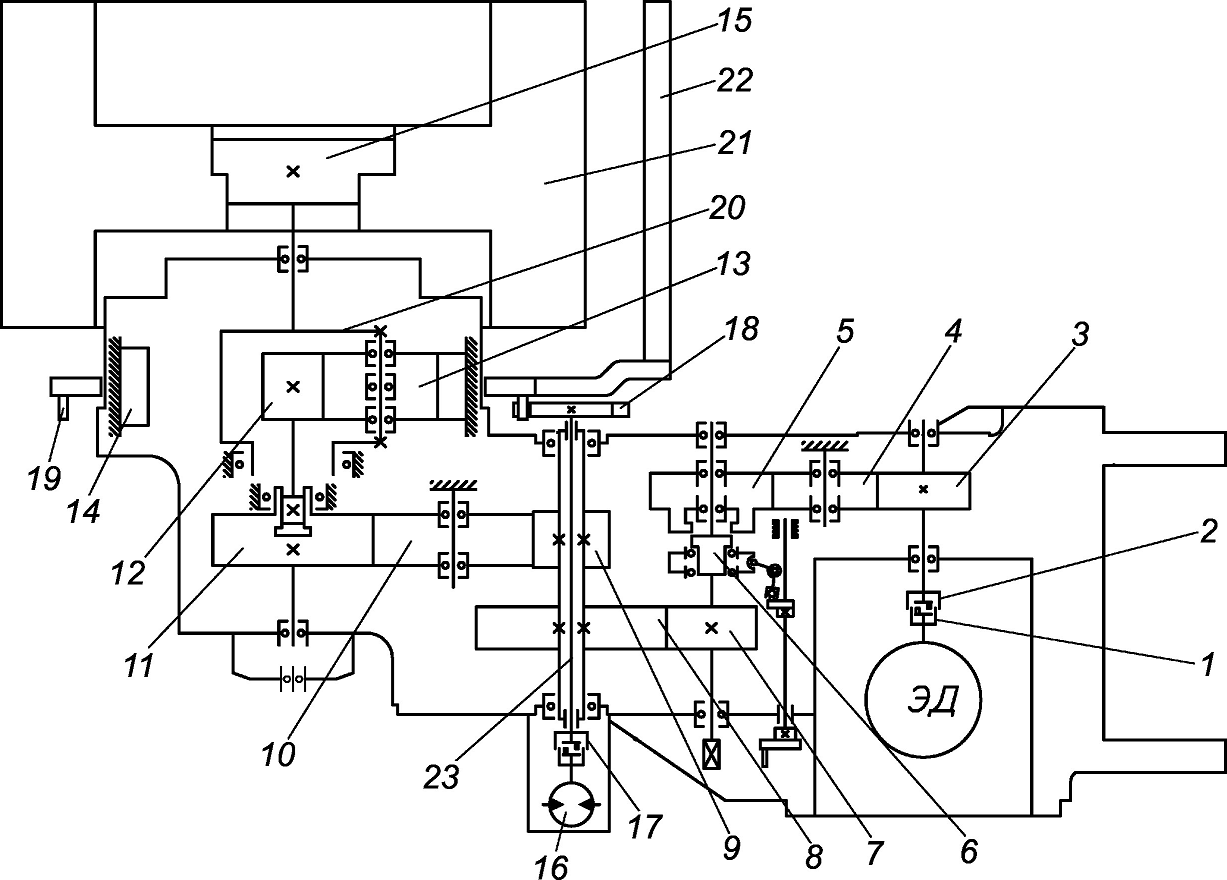
Рис.1 – Кінематична схема блоку приводу виконавчого органу КДК500
Для проведення досліджень динамічних процесів блоку приводу виконавчого органу, розроблена спрощена математична модель приводу, що враховує кінематичні складові навантаження. Ця модель дозволила отримати попередні дані про формування кінематичних навантажень в приводі.
Для вирішення поставленого завдання - розробці математичної моделі приводу виконавчого органу КДК 500, були прийняті такі допущення:
- що всі елементи схеми зводяться до системи із зосередженими дискретними масами ротора електродвигуна з приєднаними масами редуктора і виконавчого органу з приєднаними масами вихідного валу;
- пружні і дисипативні властивості приводу прийняті лінійними і характеризуються коефіцієнтами жорсткості з і опору β;
- згинні деформації вала, радіальні деформації їх опор - підшипникових вузлів - прийняті у вигляді лінійних функцій результуючого вектора радіального навантаження, що діє на ВО, і характеризуються коефіцієнтами жорсткості С і опору β;
- між крутильними і поперечними коливаннями ВО відсутній внутрішній динамічний зв'язок.
Еквівалентна розрахункова схема для складання математичної моделі представлена на анімації:
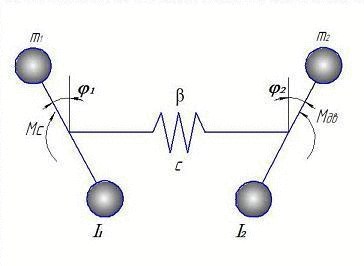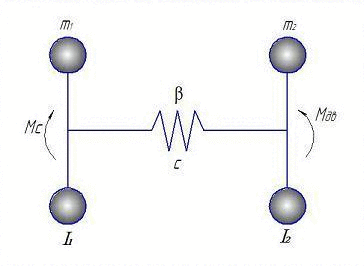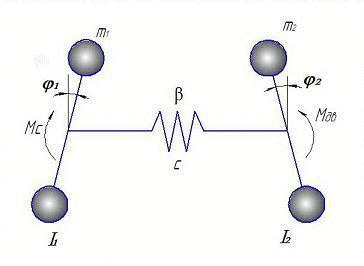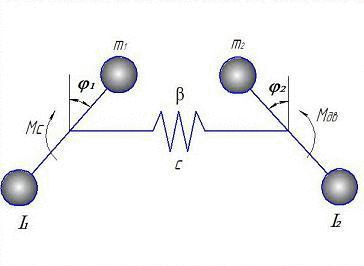
Рисунок 2 - Розрахункова двомасових модель (Анімація зроблена за допомогою GIF Animator. Складається з 6 кадрів з інтервалом в 500 мс.)
На представленій розрахунковій двохмасовій системі, I1 - це моменти інерції ротора електродвигуна, I2 - виконавчого органу, с - коефіцієнт жорсткості і β - коефіцієнт опору.
За узагальнені координати прийняті φ1, φ2, – кути повороту відповідно ротора электродвигуна і виконавчого органу, що відповідають масам з моментами інерції I1 … I2, а також електромагнітний момент двигуна Мд. Усі параметри розрахункової динамічної схеми приведені до валу ВО [6],[11].
Складена математична модель приводу виконавчого органу була здійснена з використанням фундаментальних рівнянь Парка-Горева, а також з використанням рівнянь Лагранжа II роду, внаслідок чого отримана наступна система нелінійних диференціальних рівнянь :
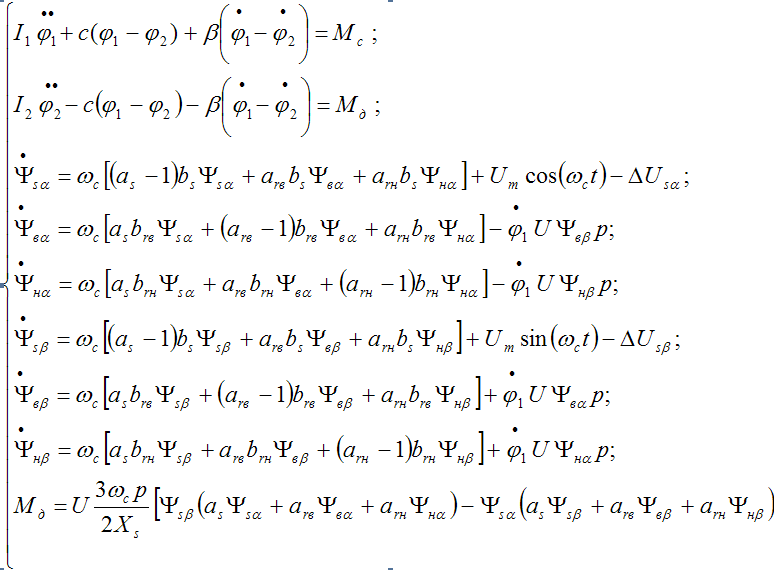
Перші два рівняння системи описують рух інерційних мас приводу виконавчого органу, наступні сім - динамічні процеси, що протікають в асинхронному електродвигуні [2],[3].
Для опису динаміки асинхронного електродвигуна в якості узагальнених координат використовуються потокозчеплення статора і ротора ψsα, ψвα, ψнα, ψвβ, ψнβ, ψsβ.
В основу алгоритму і програми моделювання динамічних складових навантаження покладений метод Рунге-Кутта четвертого порядку, який був використаний для вирішення СДР, з постійним кроком інтеграції. Вибраний метод є найбільш поширеним для вирішення подібних систем завдяки високій точності, меншій схильності до виникнення нестійкості рішення в порівнянні з іншими чисельними методами [8].
Розроблена програма дозволяє досліджувати динамічні процеси в приводі виконавчого органу в різних режимах роботи, проводити оптимізаційні обчислювальні експерименти і отримувати початкові дані для виконання міцнісних розрахунків трансмісії.
Висновки
Основні висновки, наукові і практичні результати полягають в наступному:
- 1. Розроблена комплексна імітаційна модель функціонування, що включає:
- математичну модель формування навантажень на виконавчому органі за результатами моделювання;
- математичну модель динаміки, що враховує нелінійні зв'язки, обумовлені наявністю асинхронного електродвигуна, пружної пальцьової муфти і запобіжних пристроїв (динаміка асинхронного електродвигуна описана рівняннями Парка-Горева).
Комплексна імітаційна модель адекватно описує робочий процес, разом з нелінійністю динамічних властивостей приводу і стохастичністю робочого процесу, враховує перехідні динамічні процеси в асинхронному електродвигуні і дозволяє моделювати її роботу в наступних режимах: запуск вхолосту, запуск під завалом, номінальний режим функціонування.
- 2. З використанням розробленого математичного і програмного забезпечення, а також методики проведення обчислювальних досліджень і оптимізаційних експериментів отримані і обгрунтовані оптимальні структура і параметри приводу виконавчого органу.
При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: грудень 2013 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.
Перелік посилань
- Сивокобыленко В.Ф., Костенко В.И. Математическое моделирование динамических режимов двухдвигательного асинхронного электропривода // Извести вузов. Энергетика.– Минск, 1974. – № 1. – с. 43-48.
- Гуляев В.Г., Сивокобыленко В.Ф., Жуков К.В. Математическая модель двухдвигательного привода исполнительных органов очистного комбайна // Труды Донецкого государственного технического университета. Выпуск 7, серия горно-электромеханическая. ДонГТУ. – Донецк, – 1999. – с. 97-102.
- Пинчук И.С. Переходные процессы в асинхронных электродвигателях при периодической нагрузке // Электричество. – 1957. – № 9. – с. 27-30.
- Гуляев В.Г. Проектирование и конструирование горных машин и комплексов. Часть 1. Выемочные комбайны //ГВУЗ "ДонНТУ", Технопарк ДонНТУ "УНИТЕХ", 2011.- 322с.
- Малеев Г.В., Гуляев В.Г., Бойко Н.Г., Горбатов П.А., Межаков В.А. Проектирование и конструирование горных машин и комплексов. – М.: Недра, 1988. – 368 с.
- Тарасенко В.А. Проведение вычислительных экспериментов с использованием сложных имитационных моделей горных машин // XXI столетие – проблемы и перспективы освоения месторождений полезных ископаемых: Сб. науч. трудов НГА Украины. № 3, Том 6. Горные машины и комплексы. – Днепропетровск: РИК НГА Украины, – 1998. – с. 71-75.
- Докукин А.В., Красников Ю.Д., Хургин З.Я. и др. Динамические процессы горных машин.– М.: Наука, 1972. – 150 с.
- Кондрахин В.П., Гуляев В.Г., Головин В.Л. Имитационная математическая модель динамических процессов очистных комбайнов высокой энерговооруженности с вынесенной системой подачи / Наукові праці донецького національного технічного університету. Випуск 12 (113). Серія гірничо-електромеханічна. Донецьк,2006.- с. 123-130.
- Нечепуренко М.С. Обоснование параметров и разработка узлов горных машин с упругим преобразователем движений.– Автореф. дисс… канд. техн. наук: 05.05.06 –Донецк, 1987. – 18 с.
- Докукин А.В. Оптимизация привода выемочных и проходческих машин. – М.: Недра, 1983. – 264 с.
- Тарасенко В.А. Моделирование рабочих процессов и обоснование параметров шахтной одновалковой дробилки для крепких пород. Диссертация на соискание учёной степени кандидата технических наук по специальности – ДонНТУ, Донецк, 2000.
