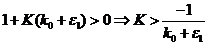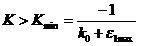ДонНТУ   Портал магістрів

Реферат за темою випускної роботи

Зміст

Вступ

Теорія автоматичного регулювання як жива бурхливо розвивально теорія, що має прямий вплив на розвиток продуктивних сил суспільства, наблизилася до вирішення багатьох складних завдань, вирішення яких ще донедавна було немислимим. З розвитком засобів зв'язку і комунікацій з'явилася можливість побудови так званих мережевих систем управління, в яких середовищем передачі інформації від датчиків до регулятора і від нього - до виконавчого механізму об'єкта управління є телекомунікаційна мережа, ресурси якої одночасно використовуються багатьма учасниками мережі. В результаті відомої невизначеності, що вноситься телекомунікаційною мережею (затримки в передачі інформації через колізії в мережі, втрата пакетів в мережах з пакетною передачею інформації, джіттер тощо) у системі автоматичного управління об'єктом погіршується якість регулювання, змінюється запас стійкості, що може призвести навіть до втрати стійкості системи. Найважливішим завданням аналізу динамічних систем управління є вирішення питання про їх стійкості. Технічне поняття стійкості систем автоматичного управління відображає властивість технічної системи не тільки стабільно працювати в нормальних режимах, та  «не йти в рознос» при відхиленні всіляких параметрів системи від номіналу і вплив на систему дестабілізуючих впливів, тобто здатності системі повертатися до рівноважного стану, з якого вона виводиться возмущающими або керуючими впливами. Стійкість системи - технічна вимога в ряду більш складних вимог, пов'язаних з показниками якості і точності САУ.


1. Актуальність теми

При моделюванні систем управління облік невизначеності завжди був однією з основних завдань. Одна з перших моделей невизначеності (нелінійна) була запропонована в роботах А.П. Лур'є (1951), М.А. Айзермана (1961), Ф.Р. Гантмахер (1967). Моделі параметричної невизначеності в лінійних системах з'явилися пізніше. Їх систематичне вивчення почав І. Горовіц (1970). Важливий напрямок в аналізі невизначеності пов'язано з моделлю невідомих, але обмежених збурень. Великий внесок у цей напрям внесли А.Б. Куржанський і Ф. Л. Черноусько. Моделі частотної невизначеності інтенсивно розроблялися в 1980 рр.., Імовірнісний підхід до робастности отримав великий розвиток в останнє десятиліття.

 

Задачу про стійкість інтервального сімейства поліномів вперше детально розглянув S. Faedo (1953). Однак він отримав тільки достатні умови робастної стійкості, засновані на інтервальному аналогу алгоритму Рауса. Більш ранній результат по робастної стійкості отримали Л. Заде і Ч. Дезоер. Потім В.Л. Харитонов довів критерій стійкості інтервального сімейства поліномів, що було великим просуванням у цій галузі (1978). Далі в цьому напрямку, в якості найбільш відомих результатів, можна відзначити реберную теорему - отриману в 1988 р. (AC Bartlett, CV Hollot, H. Lin) і графічний критерій робастної стійкості поліномів доведений - в 1990 р. (Б.Т. Поляк , Я.З. Ципкин).

 

Основними завданнями робастної стійкості, з одного боку, було визначення меж стійкості в просторі параметрів системи першого наближення (І.А. Вишнеградський), а з іншого, отримання оцінок області асимптотичної стійкості розрахункових режимів вихідних систем.

 

Дослідження стійкості систем управління за наявності невизначеності в просторі параметрів (робастного теорія) є досить важливим і актуальним напрямком наукових досліджень, тому дозволяє, на етапі проектування, визначити, чи є стійким весь клас розглянутих систем. Це дозволяє забезпечити безпечне функціонування керованого об'єкта, незважаючи на те, що в процесі виготовлення і експлуатації його параметри хоча і можуть відрізнятися від розрахункових, але гарантовано будуть відповідати стійкому поведінці цього об'єкта, тому що вони належать області робастної стійкості. Зауважимо, що розробка методів вирішення завдань робастної стійкості, є досить складною проблемою. Наприклад: стійкість всіх вершинних і реберних матриць сімейства не забезпечує робастної стійкості всього цього сімейства і, тому на практиці, зусилля інженерів і конструкторів спрямовані на вирішення конкретних завдань.

 

Методи розрахунку робастної стійкості систем управління (робастного керування) включають в себе як відомі підходи, наприклад, теорію збурень, так і нові: μ-аналіз (JC Doyle, A. Packard, Б.Т. Поляк) і імовірнісний підхід до робастности (RF Stengel, LR Ray та ін.)

 

Розробки і створення методів дослідження різних завдань робастної стійкості присвячено безліч робіт, що належать як вітчизняним, так і зарубіжним ученим, таким як І.А. Вишнеградський, Я.З. Ципкин, Б.Т. Поляк, В.Л. Харитонов, П.С. Щербаков, А.С. Немирівський, Ю.П. Петров, М.Г. Сафонов, B.R. Barmish, J. Ackermann, V. Blondel, J. Kogan, R. Tempo, D.D. Siljak та ін

 

Актуальність досліджень робастної стійкості в системах управління диктується, по-перше, сучасними потребами науки і техніки та її додатками в практичних завданнях, пов'язаних з конструюванням і моделюванням процесів управління в техніці, економіці, біології і т.д., по-друге, наявністю великої числа невирішених завдань, прямо пов'язаних з інженерною практикою. Фактично результати, отримані в теорії робастної стійкості, дозволяють забезпечувати динамічну безпеку керованих систем на етапі їх конструювання та експлуатації.

 

Робота присвячена розробці нових і розвитку найбільш конструктивних аналітичних методів і алгоритмів аналізу робастної стійкості і нестійкості систем управління. Це дослідження проводиться з єдиних позицій - системного аналізу робастного поведінки керованих систем в цілому, при цьому робастного стійкість цих систем розглядається як окремий випадок робастної нестійкості.[1]

2. Мета і задачі дослідження 

Мета: Дослідження методів забезпечення робастної стійкості та робастного якості цифрових систем управління


     Завдання:

 

1.  Аналіз методів робастної стійкості

 

2.  Аналіз методів робастного якості цифрових систем управління

 

3.  Аналіз параметричних і непараметричних невизначеностей

               3.1 Вплив адитивної і мультиплікативної невизначеності на стійкість системи автоматичного управління.

4. Аналіз сучасних програмних засобів використовуваних для оцінки показників якості робастної системи.[1]

3. Робастне управління

Робастність - властивість системи зберігати якість функціонування в межах пропонованих до неї вимог при зміні її параметрів або структури.[2]

 Робастное управління - сукупність методів теорії управління, метою яких є синтез такого регулятора, який забезпечував би гарна якість управління, якщо об'єкт управління відрізняється від розрахункового або його математична модель точно невідома.[3]

 Робастні системи - системи, що володіють властивістю робастности.

 Завдання синтезу робастних систем управління полягає в пошуку закону керування, який зберігав би вихідні змінні системи і сигнали помилки в заданих припустимих межах, незважаючи на наявність невизначеностей в об'єкті управління.[4,5] Зазвичай робастні контролери застосовуються для керування об'єктами з невідомої або неповної математичною моделлю, і містять невизначеності (рис.1).

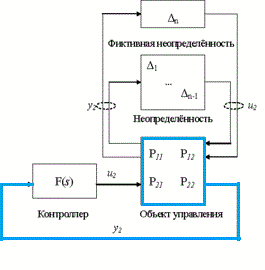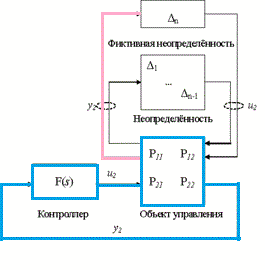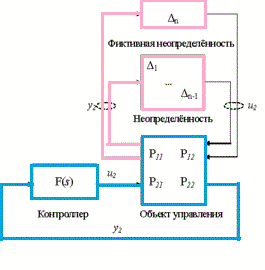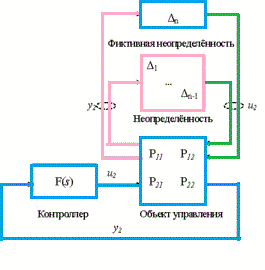
Рисунок – 1 Система автоматичного управління з невизначеністю

 

(анімація: 8 кадрів, затримка між кадрами 1с, кількість циклів відтворення 20, розмір 20 Кбайт, Easy GIF Animator)

 4. Параметричні невизначеності

Параметрична невизначеність - структура моделі відома, але її параметри можуть змінюватися в деяких межах.[6,7]

 Розглянемо систему, в якій:

- Об'єкт управління

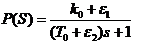
- Регулятор-підсилювач

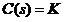
- Характеристичний поліном замкнутої системи

          Замкнута система стійка якщо:  

         Отже умова робастної стійкості прийме вигляд:


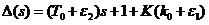
5. Непараметричні невизначеності

Непараметрична невизначеність задає допустиму помилку в частотній області.
Аддитивна невизначеність і мультиплікативна невизначеність
Кожен об'єкт управління  F(s) як елемент безлічі об'єктів зверху обмежений помилкою в адитивної формі і може бути формально представлений наступною структурною схемою (рис.2)

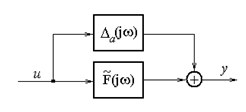
Рисунок 2 – Номінальний F (jw) об'єкт управління з адитивною помилкою

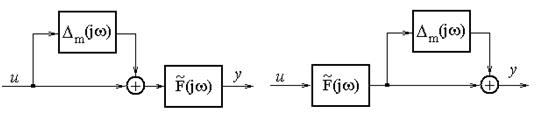
Структурна схема об'єктів з мультиплікативної невизначеністю показана на рис.3


Рисунок 3 - Об'єкти управління з мультиплікативної похибкою
Адитивні і мультиплікативні неопределенноості моделі об'єкта управління не можуть використовуватися для представлення безлічі об'єкта у яких у наслідку зміни параметрів або в слідстві структурної невизначеності появляються додаткові полюси праворуч від комплексної осі, тобто об'єктів у яких кількість «правих» полюсів може змінюватися.[8,9,10]

Теорема про малий коефіцієнті підсилення:

система з регулятором C (s) і номінальним об'єктом P0 (s) робастного стійка, якщо для будь-якої частоти ω виконується нерівність:

де W0 (jw) - передавальна функція номінальної замкнутої системи:

Рисунок 4 - Представлення класичного контуру управління (структура а) узагальненої структурою (структура б)

5. Критерії стійкості для цифрових систем


Всі критерії стійкості, які використовуються для аналізу стійкості безперервних систем, можуть бути використані для дискретних систем з урахуванням деяких особливостей.

критерій Гурвіца

Критерій стійкості Гурвіца можна використовувати при застосуванні білінійної перетворення. Розглянь алгоритм його використання.

1. Записуємо характеристичне рівняння D (z) = 0



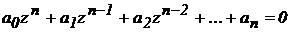
2. Виконуємо підстановку, при цьому одержимо характеристичне рівняння D (w) = 0, тобто у формі білінійної перетворення

3. Складаємо визначник Гурвіца

4. Визначаємо стійкість також як і для безперервних систем.

Лінійна дискретна система стійка, якщо при a0> 0 визначник Гурвіца і всі його діагональні мінори позитивні.

Розглянемо окремі випадки.

При n = 1 характеристичне рівняння має вигляд

Умова стійкості: a0> 0, a1> 0, а також: a0 - a1> 0.

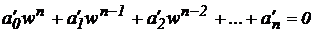
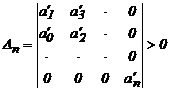
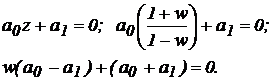
При n = 2 характеристичне рівняння має вигляд

Умова стійкості: a0> 0, a1> 0, a2> 0, а також:

 

a0 - a1 + a2> 0, a0 - a2> 0.

Критерій стійкості Михайлова з використанням білінійної перетворення

При цьому вихідним є характеристичний поліном у формі z-перетворення. Виконаємо підстановку


Нехай: w = jl, де l-фіктивна частота (0 £ l £ ¥).

При цьому критерій Михайлова для дискретних систем застосовується в такому ж вигляді, як і для безперервних систем.

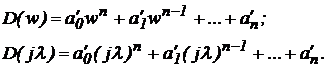
Критерій стійкості Найквіста

Розглянемо функцію, яка пов'язує характеристики розімкнутих і замкнутих дискретних систем

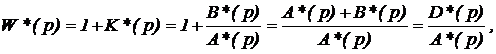
де D * (p) - характеристичний поліном замкнутої системи;

A * (p) - характеристичний поліном розімкнутої системи.

Відповідно зі слідством з принципу аргументу


Розглянемо різні випадки.

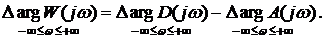
Система, стійка в розімкнутому стані

Так як разомкнутая дискретна система стійка, то вона не містить коренів у правій півплощині (тобто m = 0), для того щоб і замкнута дискретна система була стійка, повинна виконуватися умова


Формулювання критерію Найквіста:

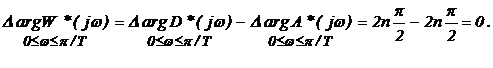
Замкнута дискретна система стійка, якщо амплітудно-фазова частотна характеристика розімкнутої стійкої системи не охоплює точку з координатами ((-1, j0)

Графічно це позначає, що годограф вектора W * (jw) не охоплює початку координат, а вектора K * (jw)-точку з координатами (-1, j0).

Система, нестійка в розімкнутому стані

Так як разомкнутая система нестійка, то вона містить m коренів у правій півплощині, для того щоб замкнута система була стійка, має виконуватися умова:

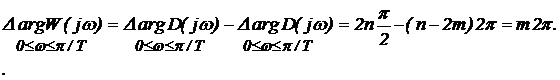
Графічно це позначає, що годограф вектора K (jw) охоплює точку з координатами (-1, j0) m-разів.

Формулювання критерію Найквіста: Замкнута дискретна система стійка, якщо амплітудно-фазова частотна характеристика розімкнутої нестійкою системи, що має m коренів у правій півплощині, охоплює току з координатами (-1, j0) m разів



Висновки

На даний момент було проведено дослідження існуючих методів оцінки робастної стійкості та робастного якості. Отримані в ході дослідження результати, будуть враховуватися при подальшому написанні магістерської роботи. На момент написання даного реферату кваліфікаційна робота ще не завершена. Дата остаточного завершення роботи: грудень 2013 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.

Перелік посилань

1.  Дорф Р., Бішоп Р. Автоматика. Сучасні системи управління. 2002р. - 832с.

2.  Харазов В. Г. Інтегровані системи управління технологічними процесами: Довідник. Видавництво: професія, видавництво, 2009. - 550С.

3.  Чебурахін І. Синтез дискретних керуючих систем та математичне моделювання: теорія, алгоритми, програми. Вид-во: НДЦ РГД, ФИЗМАТЛИТ ®, 2004. - 248c.

4. Черних І.В. Моделювання електротехнічних пристроїв в MATLAB. SimPowerSystems і Simulink / І.В. Черних - М.: ДМК Пресс, 2007. - 288 с., Іл. (Серія «Проектування»).

5. Штокман І.Г. Проектування і конструювання транспортних машин і комплексів / І.Г. Штокман - М.: Надра, 1986. - 392 с.

6.Ушаков. Л Синтез дискретних регуляторів за допомогою ЕОМ / . .: Машинобудування 1983 – 437с..

7. Н.Т. Кузовков. Модальне керування та спостерігають пристрою. М.: Машинобудування 1976–  342с.  

9. ономаренко Т.О. Обоснаванія параметрів автоматизованого управління температурними режимами рекуперативного нагрівального колодязя [Електронний ресурс] / Портал магістрів ДонНТУ, 2011- http://masters.donntu.ru/2008/fema/ponomarenko/diss/index.htm

10. Кирилов А.Г.Мікроконтроллерная система управління для динамічного об'єкта з розподіленими параметрами [Електронний ресурс] / Портал магістрів ДонНТУ, 2013 - http://masters.donntu.ru/2013/fknt/kyrylov/diss/index.htm