Abstract
Content
- 3. Robust control
- 4. Parametric uncertainty
- 5. Non-parametric uncertainty
- 6. Sustainability criteria for digital systems
- Conclusion
- References
Introduction
The theory of automatic regulation of the rapidly progressing as a living theory, which has a direct impact on the development of the productive forces of society come nearer to solving many complex tasks which until recently was unthinkable. With the development of communication and communication opportunity to build the so-called network management systems, in which the medium of transmitting information from the sensors to the controller from him - to the actuator control object is a telecommunication network, the resources of which are simultaneously used by many members of the network. As a result, certain uncertainties introduced by the telecommunications network (the delay in the transmission of information from network collisions, the loss of packets in a packet network data, jitter, etc.) in the control object machine deteriorates quality control stability margin changes, which can lead even loss of stability of the system. The most important task of the analysis of dynamic systems management is the solution to the question of their stability. Technical concept of stability of automatic control systems reflects the property of the technical system is not only stable operation under normal conditions, but "do not go hawking" when you reject all kinds of system parameters of the nominal system and the effect on the destabilizing effects, ie, the ability of the system to return to equilibrium, from which it is derived disturbing or control actions. The stability of the system - a technical requirement in a number of more complex requirements associated with quality and precision of ACS1. Relevance of the topic
.
In the simulation of control systems account of uncertainty has always been a major concern. One of the first models of uncertainty (non-linear) was proposed in AP Lurie (1951), MA Yzerman (1961), FR Gantmakher (1967). Model parametric uncertainties in linear systems appeared later. They began a systematic study of I. Horowitz (1970). An important trend in the analysis of the uncertainty associated with the model unknown but bounded disturbances. A large contribution to this destination have AB Kurzhanskii and F. Chernous'ko. Models frequency uncertainty intensively developed in the 1980s., A probabilistic approach to the robustness got great development in the last decade.
The problem of the stability of the interval family of polynomials for the first time in detail the S. Faedo (1953). However, he received only sufficient conditions for robust stability based on interval analogue Routh algorithm. The earlier results on the robust stability were Zadeh and C. Dezoer. Then VL Kharitonov proved stability criterion interval family of polynomials, which is a great advancement in this area (1978). Further in this regard, as most of the known results, we note edged theorem - obtained in 1988 (AC Bartlett, CV Hollot, H. Lin) and a graphical criterion of robust stability of polynomials proven - in 1990 (Boris Polyak , YZ Zipkin).
The main objectives of the robust stability, on the one hand, a definition of the boundaries of stability in the parameter space of the first approximation (IA Vyshnegradsky), and on the other, to obtain estimates of the asymptotic stability of the calculated modes of the original systems.
Investigation of the stability control systems in the presence of uncertainty in the parameter space (a robust theory) is very important and topical area of research, since allows the design phase, to determine whether sustainable entire class o
f these systems. This ensures safe operation of the controlled object, despite the fac
t that during manufacture and operation although its parameters, and may differ from the calculated values, but will respond guaranteed sustainable behavior of the object, as they belong to the domain of robust stability. Note that the development of methods for solving the problems of robust stability, is a very complex problem. For example, the stability of all vertex and edge matrices of the family does not provide the robust stability of the family and, therefore, in practice, the efforts of engineers and designers focused on solving specific problems.
Methods for calculating the robust stability control systems (robust control) include both well-known approaches, such as perturbation theory, and new: μ-analysis (JC Doyle, A. Packard, BT Polyak) and a probabilistic approach to robustness (RF Stengel, LR Ray et al.)
Development and creation of research methods different tasks robust stability has been widely discussed, belonging to both domestic and foreign scholars such as IA Vyshnegradsky, YZ Zipkin, BT Polak, VL Kharitonov, PS Shcherbakov, AS Nemirovsky, JP Petrov, M. Safonov, B.R. Barmish, J. Ackermann, V. Blondel, J. Kogan, R. Tempo, D.D. Siljak, etc.
Importance of the study of robust stability in control systems is dictated, first, the needs of the modern science and technology and its applications in practical problems associated with the design and simulation of control processes in engineering, economics, biology, etc., and second, the large number of unsolved problems directly related to engineering practice. In fact, the results
obtained in the theory of robust stability, security can provide dynamic control systems on the stage of their construction and operation.
The work is devoted to the development of new and more constructive development of analytical methods and algorithms to analyze the robust stability and instability of control systems. This study is carried out with one voice - the system analysis of the robust behavior of managed systems in general, and the robust stability of these systems is considered as a special case of robust instability [1]
2. The purpose and objectives of the study
Objective: Investigate methods to ensure robust stability and robust quality of digital control systems.
objectives:
1. Analysis of methods for robust stability
2. Analysis of the methods of the robust quality of digital control systems
3. The analysis of parametric and non-parametric uncertainties
3.1 Effect of additive and multiplicative uncertainty on the stability of the automatic control system.
4. Analysis of modern software tools used for assessing the quality of a robust system
.
3. Robust control
Robustness - property of the system to maintain the quality of functioning within its demands when you change the parameters or structure.[2]Robust control - a set of techniques of control, the purpose of which is the synthesis of such a regulator that would ensure good quality control, if the control object is different from the design or its mathematical model is not precisely known.[3]
Robust systems - systems which have the property of robustness.
The problem of synthesis of robust control systems is to find a control law, which would keep the output variables of the system and fault signals in predetermined acceptable range, despite the uncertainties in the facility management. [4,5]Typically, robust controllers are used to control objects with unknown or incomplete mathematical model, and contain uncertainty (Figure 1)
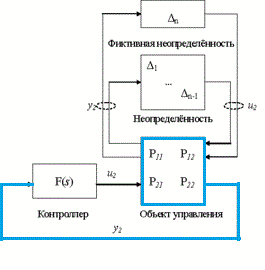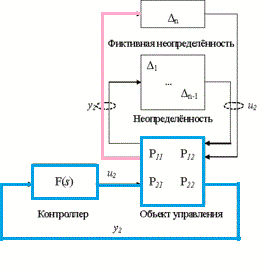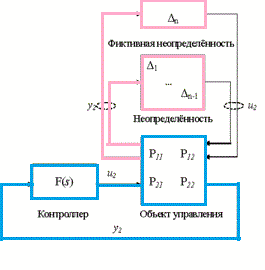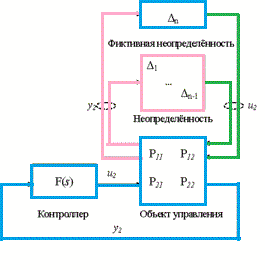
Figure - 1 Automatic
control system
with uncertainty
(Animation: 8 frames, the
delay
between shots 1s, the number of cycles of reproduction 20, size 20 KB,
Easy GIF Animator)
4. Parametric uncertainty
Parametric uncertainty - the structure of the model is known, but its parameters can be changed within certain limits.[6,7]Consider a system in which:
- Facility management
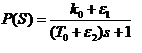
- Controller Amplifier
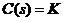
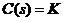
- The characteristic
polynomial of the
closed system
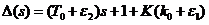
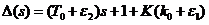
Closed-loop
system will
be stable at:
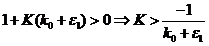
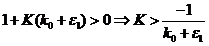
Следовательно
условие робастной устойчивости примет вид:
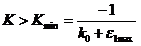
5. Non-parametric uncertainty
Non-parametric uncertainty sets the allowable error in the frequency domain.
The additive and multiplicative uncertainty uncertainty
Each control object F (s) as an element of a set of objects is limited from above error in additive form, and can be formally represented by the following block diagram (Fig. 2)
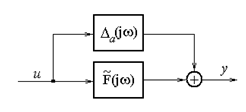
Figure 2-Rated F (jw) to control the additive error
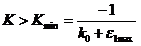
5. Non-parametric uncertainty
Non-parametric uncertainty sets the allowable error in the frequency domain.
The additive and multiplicative uncertainty uncertainty
Each control object F (s) as an element of a set of objects is limited from above error in additive form, and can be formally represented by the following block diagram (Fig. 2)

Figure 2-Rated F (jw) to control the additive error
The block diagram objects
with
multiplicative uncertainty is shown in Figure 3
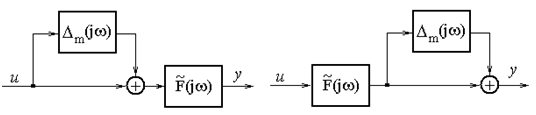
Figure 3 - Control objects with the multiplicative error

Figure 3 - Control objects with the multiplicative error
Additive and multiplicative
models
neopredelennoosti control object can not be used to represent a set of
objects for which subsequently change settings or as a consequence of
structural uncertainty poyavlyayutsya additional pole to the right of
the axis of the complex, ie, objects in which the number of "right"
poles may vary.[8,9,10]
Theorem on the small gain:
system with controller C (s) and the nominal object of P0 (s) robustly stable if for any frequency ω, the inequality:
where W0 (jw) - transfer function of the nominal closed-loop system:
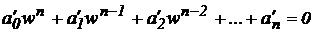
Theorem on the small gain:
system with controller C (s) and the nominal object of P0 (s) robustly stable if for any frequency ω, the inequality:
where W0 (jw) - transfer function of the nominal closed-loop system:



Figure 4 - Presentation of the classical control loop (a structure) of the generalized structure (b)
6.
Sustainability
criteria for digital systems
All stability criteria are used to analyze the stability of continuous systems may be used for systems with discrete subject to some peculiarities.
Hurwitz criterion
Hurwitz stability criterion can be used in the application of the bilinear transformation. Examine the algorithm to use.
1. Write the characteristic equation D (z) = 0
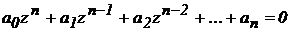
All stability criteria are used to analyze the stability of continuous systems may be used for systems with discrete subject to some peculiarities.
Hurwitz criterion
Hurwitz stability criterion can be used in the application of the bilinear transformation. Examine the algorithm to use.
1. Write the characteristic equation D (z) = 0
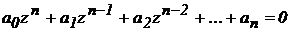
2. We perform the substitution, so obtain the characteristic equation D (w) = 0, ie, in the form of a bilinear transformation
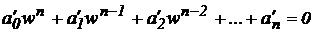
3. We form the determinant
of Hurwitz
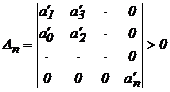
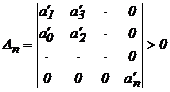
4. We determine the
stability as well as
for continuous systems.
A linear discrete system is stable, if a0> 0 Hurwitz determinant and all its diagonal minors are positive.
Consider special cases.
For n = 1 the characteristic equation of the form
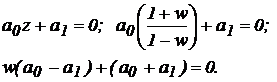
A linear discrete system is stable, if a0> 0 Hurwitz determinant and all its diagonal minors are positive.
Consider special cases.
For n = 1 the characteristic equation of the form
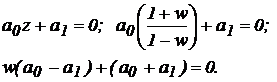
The stability condition:
a0> 0,
a1> 0, a2> 0, and:
a0 - a1 + a2> 0, a0 - a2> 0.
Mikhailov stability criterion using the bilinear transformation
This source is the characteristic polynomial of the form z-transform. to substitute
z = (1 + w) / (1-w) .
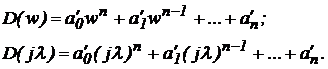
a0 - a1 + a2> 0, a0 - a2> 0.
Mikhailov stability criterion using the bilinear transformation
This source is the characteristic polynomial of the form z-transform. to substitute
z = (1 + w) / (1-w) .
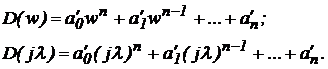
Let: w = jl, where l-dummy
frequency (0
£ l £ ¥).
In this case, the criterion Mikhailova for discrete systems is applied in the same form as for the continuous systems.
Nyquist stability criterion
Consider a function that links the characteristics of open-loop and closed discrete systems
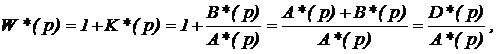
In this case, the criterion Mikhailova for discrete systems is applied in the same form as for the continuous systems.
Nyquist stability criterion
Consider a function that links the characteristics of open-loop and closed discrete systems
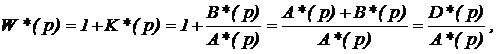
where D * (p) -
a
characteristic polynomial of a closed system;
A * (p) - the open loop characteristic polynomial.
According to the corollary of the principle of the argument
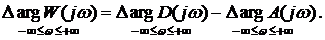
A * (p) - the open loop characteristic polynomial.
According to the corollary of the principle of the argument
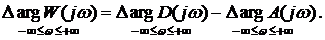
Consider the different
cases.
The system is stable in the open position
Since discrete open loop system is stable, it contains no zeros in the right half (ie, m = 0), so that discrete and closed system was stable, must satisfy the condition
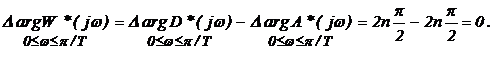
The system is stable in the open position
Since discrete open loop system is stable, it contains no zeros in the right half (ie, m = 0), so that discrete and closed system was stable, must satisfy the condition
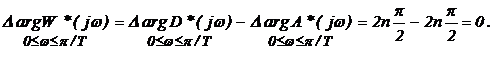
The wording of the Nyquist
criterion:
Closed discrete system is stable if the amplitude and phase frequency response of open-loop stable system does not cover the point with coordinates ((-1, j0)
Graphically, this indicates that the locus of the vector W * (jw) does not include the origin, and the vector K * (jw)-point coordinates (-1, j0).
The system is unstable in the open position
Since the open-loop system is unstable, it contains m roots in the right half-plane, so that a closed system has been stable condition must be satisfied:
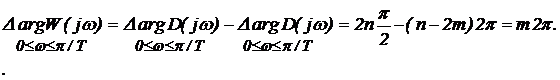
Closed discrete system is stable if the amplitude and phase frequency response of open-loop stable system does not cover the point with coordinates ((-1, j0)
Graphically, this indicates that the locus of the vector W * (jw) does not include the origin, and the vector K * (jw)-point coordinates (-1, j0).
The system is unstable in the open position
Since the open-loop system is unstable, it contains m roots in the right half-plane, so that a closed system has been stable condition must be satisfied:
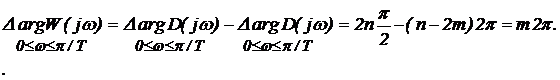
Graphically, this indicates
that the
locus vector K (jw) encloses the point with coordinates (-1, j0)
m-times.
The wording of the Nyquist criterion: Closed discrete system is stable if the amplitude and phase frequency response of open-loop unstable system with m roots in the right half-plane, covers current coordinates (-1, j0) m times.
The wording of the Nyquist criterion: Closed discrete system is stable if the amplitude and phase frequency response of open-loop unstable system with m roots in the right half-plane, covers current coordinates (-1, j0) m times.
Conclusion
At the moment, a study was conducted of existing methods for assessing the robust stability and robust quality. The findings of the research results will be taken into account when writing the master's later work. At the time of writing this essay qualification work is not yet complete. Date of final completion: December 2013. Full text of the work and materials on the topic can be obtained from the author or his manager after that date.
References
1. R. Dorf, Bishop R. Automation. Modern control systems. 2002. - 832s.2. Kharazov VG Integrated Process Control Systems: A Guide. Publisher: profession, publishing, 2009. - 550S.
3. Cheburakhin I. Synthesis of discrete control systems and mathematical modeling: theory, algorithms and programs. Publishing house: SIC RHD, FIZMATLIT ®, 2004. - 248c.
4. Chernykh IV Simulation of electrical devices in MATLAB. SimPowerSystems and Simulink / IV Black - M: DMK Press, 2007. - 288 p., Ill. (Series "Design").
5. Stockman IG Design and construction of machinery and transport systems / IG Stockman - Moscow: Nedra, 1986. - 392 p.
6 AV Ushakov.Synthesis of discrete controllers using a computer / AL: Mechanical Engineering 1983– 437р.
7. NT Kuzovkov. Modal control and watching the device. Mashinostroyeniye 1976–342р.
9. Ponomarenko TS Obosnavanie automated parameter control-temperature regenerative heating well [electronic resource] / Masters portal Donetsk National Technical University, 2011–http :/ / masters.donntu.ru/2008/fema/ponomarenko/diss/index.htm
10. Kirillov A.G.Mikrokontrollernaya management system for dynamic object with distributed parameters [electronic resource] / Masters portal Donetsk National Technical University, 2013 – http://masters.donntu.ru/2013/fknt/kyrylov/diss/index.htm
