ДонНТУ   Портал магистров

Реферат по теме выпускной работы

Содержание

Введение

 Теория автоматического регулирования как живая бурно развивающяся теория, имеющая прямое влияние на развитие производительных сил общества, приблизилась к решению многих сложных задач, решение которых еще до недавнего времени было немыслимым. С развитием средств связи и коммуникаций появилась возможность построения так называемых сетевых систем управления, в которых средой передачи информации от датчиков к регулятору и от него – к исполнительному механизму объекта управления является телекоммуникационная сеть, ресурсы которой одновременно используются многими участниками сети.   В результате известной неопределенности, вносимой телекоммуникационной сетью (задержки в передаче информации из-за коллизий в сети, потеря пакетов в сетях с пакетной передачей информации, джиттер и др.)  в системе автоматического управления объектом  ухудшается качество регулирования, изменяется запас устойчивости, что может привести даже к потере устойчивости системы. Важнейшей задачей анализа динамических систем управления является решение вопроса об их устойчивости. Техническое понятие устойчивости систем автоматического управления отражает свойство технической системы не только стабильно работать в нормальных режимах, но и «не уходить вразнос» при отклонении всевозможных параметров системы от номинала и влиянии на систему дестабилизирующих воздействий, т. е. способности системе возвращаться к равновесному состоянию, из которого она выводится возмущающими или управляющими воздействиями. Устойчивость системы - техническое требование в ряду более сложных требований, связанных с показателями качества и точности САУ. 

 

1. Актуальность

При моделировании систем управления учет неопределенности всегда являлся одной из основных задач. Одна из первых моделей неопределенности (нелинейная) была предложена в работах А.П. Лурье (1951), М.А. Айзермана (1961), Ф.Р. Гантмахера (1967). Модели параметрической неопределенности в линейных системах появились позднее. Их систематическое изучение начал И. Горовиц (1970). Важное направление в анализе неопределенности связано с моделью неизвестных, но ограниченных возмущений. Большой вклад в это направление внесли А.Б. Куржанский и Ф. Л. Черноусько. Модели частотной неопределенности интенсивно разрабатывались в 1980 гг., вероятностный подход к робастности получил большое развитие в последнее десятилетие.

Задачу об устойчивости интервального семейства полиномов впервые подробно рассмотрел S. Faedo (1953). Однако он получил только достаточные условия робастной устойчивости, основанные на интервальном аналоге алгоритма Рауса. Более ранний результат по робастной устойчивости получили Л. Заде и Ч. Дезоер. Затем В.Л. Харитонов доказал критерий устойчивости интервального семейства полиномов, что являлось большим продвижением в этой области (1978). Далее в этом направлении, в качестве наиболее известных результатов, можно отметить реберную теорему – полученную в 1988 г. (A.C. Bartlett, C.V. Hollot, H. Lin) и графический критерий робастной устойчивости полиномов доказанный – в 1990 г. (Б.Т. Поляк, Я.З. Цыпкин).

Основными задачами робастной устойчивости, с одной стороны, являлось определение границ устойчивости в пространстве параметров системы первого приближения (И.А. Вышнеградский), а с другой, получение оценок области асимптотической устойчивости расчетных режимов исходных систем.

Исследование устойчивости систем управления при наличии неопределенности в пространстве параметров (робастная теория) является весьма важным и актуальным направлением научных исследований, т.к. позволяет, на этапе проектирования, определить, является ли устойчивым весь класс рассматриваемых систем. Это позволяет обеспечить безопасное функционирование управляемого объекта, несмотря на то, что в процессе изготовления и эксплуатации его параметры хотя и могут отличаться от расчетных, но гарантировано будут отвечать устойчивому поведению этого объекта, т.к. они принадлежат области робастной устойчивости. Заметим, что разработка методов решения задач робастной устойчивости, является весьма сложной проблемой. Например: устойчивость всех вершинных и реберных матриц семейства не обеспечивает робастной устойчивости всего этого семейства и, поэтому на практике, усилия инженеров и конструкторов направлены на решение конкретных задач.

Методы расчета робастной устойчивости систем управления (робастное управление) включают в себя как известные подходы, например, теорию возмущений, так и новые: μ-анализ (J.C. Doyle, A. Packard, Б.Т. Поляк) и вероятностный подход к робастности (R.F. Stengel, L.R. Ray и др.).

Разработке и созданию методов исследования различных задач робастной устойчивости посвящено множество работ, принадлежащих как отечественным, так и зарубежным ученым, таким как И.А. Вышнеградский, Я.З. Цыпкин, Б.Т. Поляк, В.Л. Харитонов, П.С. Щербаков, А.С. Немировский, Ю.П. Петров, М.Г. Сафонов, B.R. Barmish, J. Ackermann, V. Blondel, J. Kogan, R. Tempo, D.D. Siljak и др.

Актуальность исследований робастной устойчивости в системах управления диктуется, во-первых, современными потребностями науки и техники и ее приложениями в практических задачах, связанных с конструированием и моделированием процессов управления в технике, экономике, биологии и т.д.; во-вторых, наличием большого числа нерешенных задач, прямо связанных с инженерной практикой. Фактически результаты, полученные в теории робастной устойчивости, позволяют обеспечивать динамическую безопасность управляемых систем на этапе их конструирования и эксплуатации.

Работа посвящена разработке новых и развитию наиболее конструктивных аналитических методов и алгоритмов анализа робастной устойчивости и неустойчивости систем управления. Это исследование проводится с единых позиций – системного анализа робастного поведения управляемых систем в целом, при этом робастная устойчивость этих систем рассматривается как частный случай робастной неустойчивости.[1]

 


2. Цель и задачи исследования, планируемые результаты

Цель: Исследование методов обеспечения робастной устойчивости и робастного качества цифровых систем управления.

 

Задачи:

1.     Анализ методов робастной устойчивости

2.     Анализ методов робастного качества цифровых систем управления

3.     Анализ параметрических и непараметрических неопределенностей

3.1   Влияние аддитивной и мультипликативной неопределенности на устойчивость системы автоматического управления.

 

4.     Анализ современных программных средств используемых для оценки показателей качества робастной системы.

3.Робастное управление

Робастность – свойство системы сохранять качество функционирования в пределах предъявляемых к ней требований при изменении ее параметров или структуры.[2]

Робастное управление — совокупность методов теории управления, целью которых является синтез такого регулятора, который обеспечивал бы хорошее качество управления, если объект управления отличается от расчётного или его математическая модель точно неизвестна.[3]

Робастные системы —  системы, обладающие свойством робастности.

       Задача синтеза робастных систем управления заключается в поиске закона управления, который сохранял бы выходные переменные системы и сигналы ошибки в заданных допустимых пределах, несмотря на наличие неопределённостей в объекте управления.[4,5] Обычно робастные контроллеры применяются для управления объектами с неизвестной или неполной математической моделью, и содержащими неопределённости (рис.1)

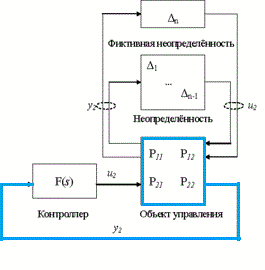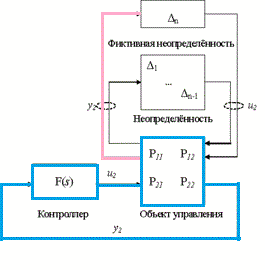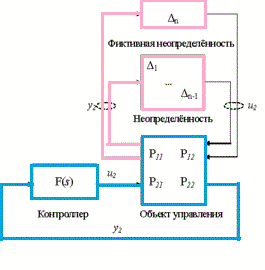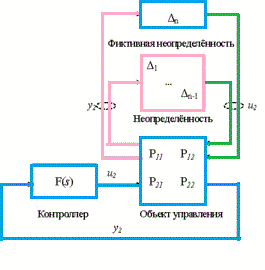
Рисунок – 1 Система автоматического управления с неопределенностью

(анимация: 8 кадров, задержка между кадрами 1с, количество циклов воспроизведения 20, размер 20 Кбайт, Easy GIF Animator)

4. Параметрические неопределенности

Параметрическая неопределенность - структура модели известна, но ее параметры могут изменяться в некоторых пределах.[6,7]

Рассмотрим систему, в которой:

 - объект управления

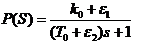
-  регулятор-усилитель

 

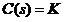
 - характеристический полином замкнутой системы

 

 


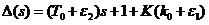
Замкнутая система будет устойчива при:

 

 

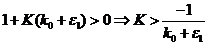
Следовательно условие робастной устойчивости примет вид:

 

 

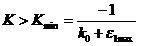
5. Непараметрические неопределенности

Непараметрическая неопределенность задает допустимую ошибку в частотной области.

Аддитивная неопределенность и мультипликативная неопределенность

Каждый объект управления  F(s) как  элемент  множества объектов сверху ограничен ошибкой в аддитивной форме и может быть формально представлен следующей структурной схемой (рис.2)

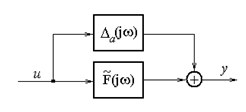
Рисунок 2–Номинальный F(jw)  объект управления с аддитивной ошибкой 

 

Структурная схема объектов с мультипликативной неопределенностью показана на рис.3

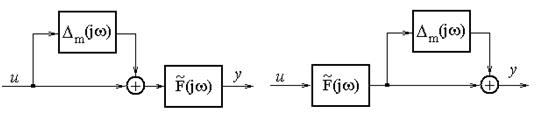
Рисунок 3 – Объекты управления с мультипликативной погрешностью

 

Аддитивные и мультипликативные неопределенноости модели объекта управления не могут использоваться для представления множества объекта у которых в последствии изменения параметров или в следствии структурной неопределенности появляються дополнительные полюса справа от комплексной оси, т.е. объектов у которых количество «правых» полюсов может меняться.[8,9,10]

Теорема о малом коэффициенте усиления:

система с регулятором C(s) и номинальным объектом P0(s)  робастно устойчива, если для любой частоты ω выполняется неравенство:

где  W0(jw)     - передаточная функция номинальной замкнутой системы:

Рисунок 4 – Представление классического контура управления(структура а) обобщенной структурой(структура б)

5. Критерии устойчивости для цифровых систем

Все критерии устойчивости, которые используются для анализа устойчивости непрерывных систем, могут быть использованы для дискретных систем с учетом некоторых особенностей.

Критерий Гурвица

Критерий устойчивости Гурвица можно использовать при применении билинейного преобразования. Рассмотри алгоритм его использования.

1.     Записываем характеристическое уравнение D(z) = 0

 

.

 

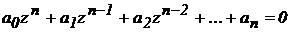2. Выполняем подстановку , при этом получим характеристическое уравнение D(w) = 0, т. е. в форме билинейного преобразования

 

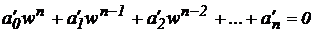
3. Составляем определитель Гурвица

 

 

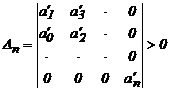
4. Определяем устойчивость также как и для непрерывных систем.

Линейная дискретная система устойчива, если при a0>0 определитель Гурвица и все его диагональные миноры положительны.

Рассмотрим частные случаи.

При n = 1 характеристическое уравнение имеет вид

 

 

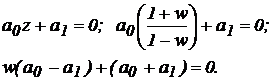
Условие устойчивости: a0 > 0, a1 > 0, а также: a0 - a1 > 0.

При n = 2 характеристическое уравнение имеет вид

 

 

Условие устойчивости: a0 > 0, a1 > 0, a2 > 0, а также:

 

a0 - a1 + a2 > 0, a0 - a2 > 0.

Критерий устойчивости Михайлова с использованием билинейного преобразования

При этом исходным является характеристический полином в форме z-преобразования. Выполним подстановку

 

z = (1+w)/(1-w) .

 

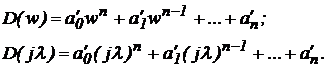
Пусть: w = jl, где l–фиктивная частота (0 £ l £ ¥).

При этом критерий Михайлова для дискретных систем применяется в таком же виде, как и для непрерывных систем.

Критерий устойчивости Найквиста

Рассмотрим функцию, которая связывает характеристики разомкнутых и замкнутых дискретных систем

 

 

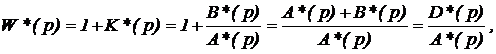
где D*(p) – характеристический полином замкнутой системы;

A*(p) – характеристический полином разомкнутой системы.

В соответствии со следствием из принципа аргумента

 

 

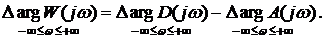
Рассмотрим разные случаи.

Система, устойчивая в разомкнутом состоянии

Так как разомкнутая дискретная система устойчива, то она не содержит корней в правой полуплоскости (т. е. m = 0), для того чтобы и замкнутая дискретная система была устойчива, должно выполняться условие

 

 

 

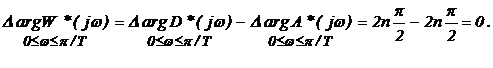
Формулировка критерия Найквиста:

Замкнутая дискретная  система устойчива, если амплитудно-фазовая частотная характеристика разомкнутой устойчивой системы не охватывает точку с координатами ((–1 , j0)

Графически это обозначает, что годограф вектора W*(jw) не охватывает начала координат, а вектора K*(jw) -точку с координатами (-1, j0).

Система, неустойчивая в разомкнутом состоянии

Так как разомкнутая система неустойчива, то она содержит m корней в правой полуплоскости, для того чтобы замкнутая система была устойчива, должно выполняться условие:

 

 

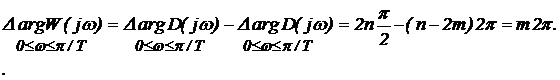
Графически это обозначает, что годограф вектора K(jw) охватывает точку с координатами (-1, j0) m –раз.

Формулировка критерия Найквиста: Замкнутая дискретная система устойчива, если амплитудно-фазовая частотная характеристика разомкнутой неустойчивой системы, имеющей m корней в правой полуплоскости, охватывает току с координатами (–1 , j0) m раз.

Выводы

На данный момент было проведено исследование существующих методов оценки робастной устойчивости и робастного качества. Полученные в ходе исследования результаты, будут учитываться при дальнейшем написании магистерской работы.  На момент написания данного реферата квалификационная работа еще не завершена. Дата окончательного завершения работы: декабрь 2013 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.


Список источников

1.   Дорф Р., Бишоп Р. Автоматика. Современные системы управления. 2002г. – 832с.

2.    Харазов В. Г. Интегрированные системы управления технологическими процессами: Справочник.              Издательство: профессия, издательство, 2009. – 550с.

3.   Чебурахин И. Синтез дискретных управляющих систем и математическое моделирование: теория,           алгоритмы, программы. Изд-во: НИЦ РХД, ФИЗМАТЛИТ®, 2004. – 248c.

4. Черных И.В. Моделирование электротехнических устройств в MATLAB. SimPowerSystems и Simulink /      И.В. Черных – М.: ДМК Пресс, 2007. – 288 с., ил. (Серия «Проектирование»).

5. Штокман И.Г. Проектирование и конструирование транспортных машин и комплексов / И.Г.              Штокман – М.: Недра, 1986. – 392 с.

6   Ушаков А.В.Синтез дискретных регуляторов при помощи ЭВМ . Л.: Машиностроение 1983 – 437с. 

7.   Н.Т. Кузовков. Модальное управление и наблюдающие устройства. М. : Машиностроение 1967–  342с.

9. Пономаренко Т.О. Обоснавание параметров автоматизированного управления температурными режимами рекуперативного нагревательного колодца [Электронный ресурс] / Портал магистров ДонНТУ, 2011 –http://masters.donntu.ru/2008/fema/ponomarenko/diss/index.htm

10. Кириллов А.Г.Микроконтроллерная система управления для динамического объекта с распределенными параметрами [Электронный ресурс] / Портал магистров ДонНТУ, 2013 – http://masters.donntu.ru/2013/fknt/kyrylov/diss/index.htm