Реферат за темою випускної роботи
Зміст
Вступ1. Актуальність теми
2. Мета і задачі дослідження
3. Стислий опис об’єкта і системи управління
4. Експериментальні дослідження
Висновки
Перелік використаної літератури
Вступ
На сьогоднішній день існує безліч реалізацій так званого балансуючого робота. За своєю суттю балансуючий робот являє собою систему підтримки рівноваги конструкції у вигляді перевернутого маятника, як правило це платформа на двох колесах. Принципи побудови даних систем схожі, проте застосовувані алгоритми стабілізації та електронні засоби в реальних моделях істотно розрізняються. При синтезі системи управління дуже важливо отримати точний математичний опис об'єкта управління, а також всіх компонент, які входять до складу системи. Це можна зробити на основі законів фізики, механіки і т.д. Однак часом знань про об'єкт недостатньо або ж параметри об'єкта можуть зміняться в деяких межах. Тоді вдаються до експериментальних методів, суть яких зводиться до статистичної обробки технологічних даних. При експериментально-аналітичному методі апріорна модель, отримана аналітичним шляхом, уточнюється у відповідних експериментах.
1. Актуальність теми
Питання стабілізації фізично нестійких об'єктів є однією з найчастіших проблем теорії автоматичного управління, з якою стикаються інженери цієї області. Тому виникає необхідність отримання багатого досвіду з вирішення подібних завдань для майбутніх інженерів. При цьому важливо отримання не лише теоретичних знань і навичок роботи з математичними моделями, а в першу чергу практичних умінь і досвіду роботи з реальними фізичними об'єктами, фізичну природу яких неможливо повністю описати за допомогою моделі.
Паралельно з цим, технічний прогрес йде шляхом мініатюризації датчиків, виконавчих механізмів, зниження їх енерговитрат і вартості та підвищення універсальності, надійності і швидкодії мікросхем і мікропроцесорів. Це створює можливість створення об'єктів, які поєднують в собі всі апаратні засоби не тільки для формування керуючого впливу, але і для вимірювання фізичних величин зворотного зв'язку і реалізації складних систем управління. Можливість повної реалізації всіх цих функцій в середині одного об'єкту дозволяє зробити його автономним і компактним.
Однією з найпоширеніших систем динамічної рівноваги є САУ робота у вигляді перевернутого маятника. Вона вже отримала широке поширення в системах автоматизації, робототехніки завдяки своїй простоті і високої маневреності. Використання для цієї системи сучасних мікроелектромеханічних систем (МЕМС-датчиків) дозволяє отримати ще більшу мініатюризацію і доступність таких систем, що дозволяє розширити область їх застосування. Для плавної стабілізації потрібно дуже точне визначення кута відхилення і розрахунок керуючого впливу з урахуванням динамічних характеристик двигунів постійного струму, які призводять балансуючого робота в стан рівноваги. Параметри двигунів можуть істотно відрізнятися навіть при напрямку обертання валу. Тому виникає необхідність ідентифікації моделі двигуна в різних режимах роботи з метою подальшого врахування цієї моделі в синтезі законів управління.
2. Мета і задачі дослідження
Головною метою магістерської роботи є проектування та практична реалізація автоматичної системи підтримки динамічної рівноваги балансуючого робота, виконаного у вигляді конструкції типу перевернутий маятник
.
Основні завдання дослідження:
- Аналіз існуючих систем стабілізації і динамічної рівноваги.
- Аналіз наявних методик ідентифікація моделей подібного типу.
- Розробка математичної моделі об'єкта.
- Розробка функціональної та структурної схем об'єкта.
- Моделювання динамічних процесів в об'єкті.
- Аналіз існуючих методів визначення кута нахилу конструкції та обробки показань з датчиків.
- Дослідження методик ідентифікації положення об'єкта.
- Синтез алгоритмів ідентифікації параметрів балансуючого робота (параметри двигуна, кут нахилу, положення в просторі).
- Уточнення математичної моделі та програмування алгоритмів обробки показників датчиків.
- Розробка стендової моделі балансуючого робота.
3. Стислий опис об'єкта і системи управління
Конструкція балансуючого робота є досить простий і саме тому має ряд корисних властивостей. Спрощена конструкція балансуючого робота зображена на малюнку 3.1. Наявність двох коліс зменшує габарити і підвищує надійність, а роздільне управління кожним з них (за допомогою двигунів постійного струму) робить платформу дуже маневреною, зокрема платформа може повертати рухаючись або виконувати розворот на місці. Проте головним недоліком є те, що платформа нестійка і при вимкнутих двигунах платформа втратить баланс і впаде. Однак зробити платформу стійкої покликана система автоматичного управління. Створивши замкнутий контур, постійно вимірюючи кут відхилення, є можливість виробляти управляючі впливи з великою частотою, щоразу корегуючи положення платформи.

Рисунок 3.1 — Платформа у вигляді перевернутого маятника
Ідея підтримки балансу досить проста. Конструкція має єдину точку рівноваги коли центр мас вантажу знаходиться безпосередньо над віссю обертання. Якщо центр ваги конструкції відхиляється убік, то сила тяжіння частково передається через опору до землі, а інша її складова створює момент обертання конструкції, який прагне повалити конструкцію на бік. Щоб компенсувати цю силу, система повинна почати рух з прискоренням в бік падіння. Сила F, яку створює прискорення також розкладається на силу діючу в бік опори, і силу, яка створює зворотний момент обертання конструкції.
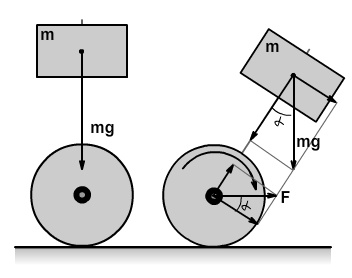
Рисунок 3.2 — Фізична модель об'єкта
Тобто для підтримки балансу необхідне виконання умови:
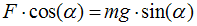
Але якщо розглядати тільки малі відхилення від стану рівноваги (α → 0), то завдяки лінеаризації можна отримати більш просте умова для рівноваги:
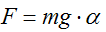
Таким чином процес підтримки рівноваги такої системи можна розділити на дві основні складові: визначення кута нахилу конструкції від стану рівноваги і управління обертанням коліс залежно від величини відхилення, для формування сили, яка компенсує падіння.
Принцип підтримки рівноваги можна проілюструвати наступною анімацією.
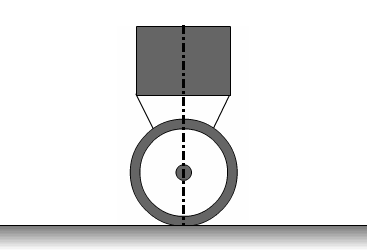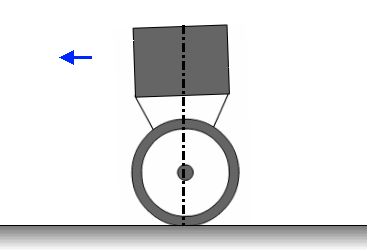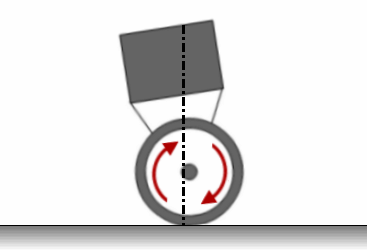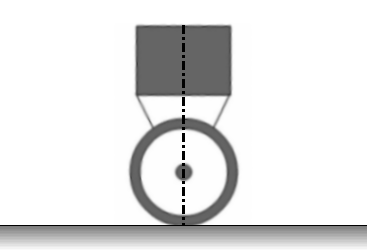
Рисунок 3.3 — Принцип стабілізації об'єкта. Анімація складається з 11 кадрів із затримкою в 500мс між кадрами. Кількість циклів повторення анімації є нескінченною.
Для визначення кута відхилення конструкції від нормалі до поверхні найбільш правильним буде використання МЕМС, яка являє собою об'єднання акселерометра і гіроскопа. Узагальнена структурна схема даної системи представлена нижче.

Рисунок 3.4 — Узагальнена структурна схема системи
В якості об'єкта управління виступає конструкція перевернутого маятника. Роль виконавчого механізму грає двигун постійного струму з вбудованим енкодером, в системі присутні два двигуни. Завдання регулювання та обчислень керуючих впливів покладені на мікроконтролер, а закон управління реалізується і задається програмно. Обидва двигуни постійного струму керуються за допомогою широтно-імпульсної модуляції (ШІМ). Мікроконтролер розраховує коефіцієнт заповнення ШІМ сигналу і напрямок обертання валу і посилає ці сигнали на драйвер двигуна.
Виходом системи є кут відхилення маятника від нормалі до поверхні, який вимірюється акселерометром і гіроскопом. Сигнали з МЕМС пропускаються через систему комплементарних фільтрів (рисунок 3.5). Різниця задаючого впливу (0 градусів) і поточного кута відхилення надходить на вхід регулятора (в нашому випадку мікроконтролера), який розраховує керуючий вплив для приведення конструкції в рівновагу.
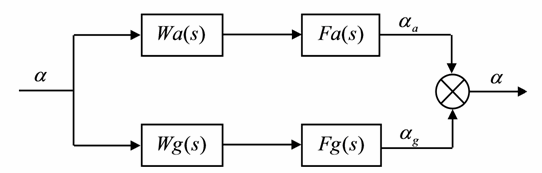
Рисунок 3.5 — Система комплементарных фільтрів
де Wa(s) — передатна функція акселерометра; Wg(s) — передатна функція гіроскопа; Fa(s) — передатна функція фільтра акселерометра; Fg(s) — передатна функція фільтра гіроскопа;  — вимірюваний кут.
— вимірюваний кут.
Метою системи комплементарних фільтрів є підтримка рівності вхідного і вихідного сигналів. Але на низьких частотах зміни кута нахилу система віддає перевагу показанням акселерометра. Це пов'язано з тим, що коли конструкція перебуває в стані, близькому до стану спокою, саме дані акселерометра найбільш відповідають дійсності, а на високих частотах — більш точні свідчення гіроскопа, який не чутливий до різких рухів конструкції. Кожен датчик домінує
на частоті сигналу, на якій вплив його недоліків є мінімальним. Даний підхід забезпечує досить високу точність вимірювань при відносній простоті реалізації. Існують також альтернативні методи обробки показників датчиків, наприклад з використанням фільтра Калмана.
4. Експериментальні дослідження
Метою ідентифікації параметрів є отримання найбільш точного математичного опису системи в цілому, а також синтез алгоритмів обробки показників датчиків і енкодерів для визначення таких параметрів як кут відхилення маятника від нормалі до поверхні, переміщення і поточна координата об'єкта. Під ідентифікацією можна розуміти як формування моделей на основі результатів спостережень, експериментів і дослідження їх властивостей, так і визначення кута відхилення за допомогою за допомогою фільтрів і визначення переміщення і координати за допомогою вбудованих енкодерів [2]. У даному розділі проведена ідентифікація структури математичної моделі двигуна, зокрема отримано рівняння зміну швидкості обертання двигуна при подачі одиничного ступеневої впливу. Отримана передатна функція в подальшому може бути врахована в синтезі закону регулювання.
Двигун постійного струму (ДПС) незалежного збудження описується наступною системою рівнянь:
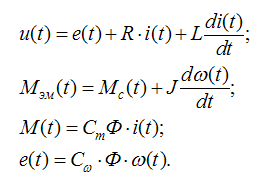
де u(t) — напруга на якірній обмотці двигуна; e(t) — е.р.с. якоря; i(t) — струм якоря; Ф — потік, який створюється обмоткою збудження; Мем (t) — електромагнітний момент двигуна; Мc(t) — момент опору руху; w(t) — швидкість обертання валу двигуна; R — активний опір якірного ланцюга; L — індуктивний опір якірного ланцюга; J — сумарний момент інерції якоря і навантаження; Cw — електромагнітна постійна двигуна; Cm — механічна постійна двигуна.
Для створення моделі двигуна необхідно отримати передавальні функції, застосувавши до диференціальних рівнянь перетворення Лапласа. Передавальна функція, яка характеризує струм якоря і падіння напруги на якорі:
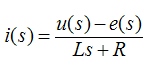
Передатна функція, яка пов'язує динамічний момент і швидкість обертання вала двигуна:
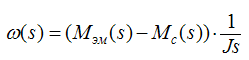
Використовуючи отримані передавальні функції можна скласти структурну схему моделі двигуна постійного струму, яка представлена на рисунку 4.1. Оскільки динамічні характеристики двигуна заздалегідь не відомі, задамося довільними даними і виконаємо моделювання швидкості обертання двигуна: L=0,001 Гн, R=61 Ом, CmFi=0,22, J=0,0004 кг*м2.
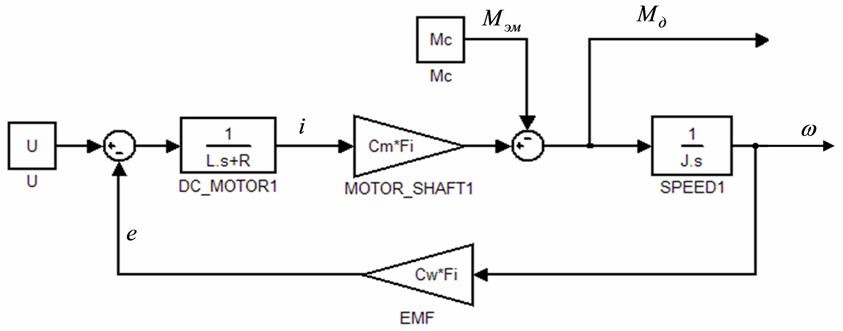
Рисунок 4.1 — Структурна схема двигуна постійного струму
Промоделювавши роботу моделі з вхідним впливом рівним 18 вольт був отриманий графік перехідного процесу швидкості обертання валу двигуна.
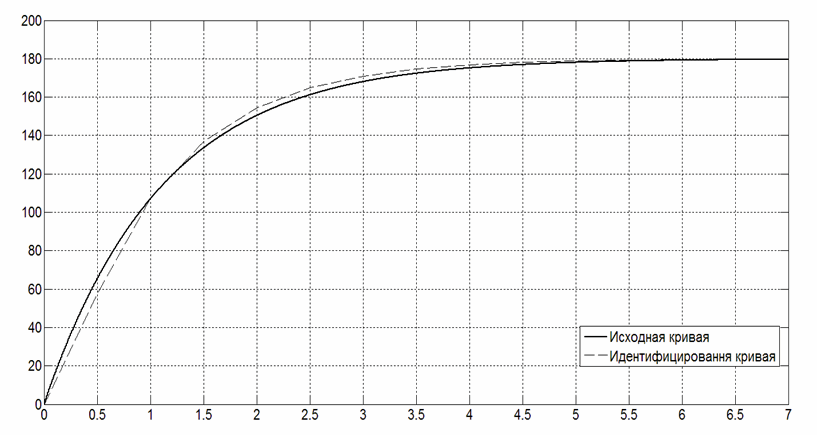
Припустивши, що крива розгону на рисунку 4.2 була отримана експериментально, тобто були оброблені дані вбудованого в двигун енкодера, проведемо ідентифікацію динамічних характеристик двигуна методом Сімою [1]. Даний метод є одним з найбільш зручних при використанні ЕОМ для ідентифікації об'єкта управління в умовах проведення активного експерименту. Кінцеву модель об'єкта будемо шукати у вигляді типової кривої розгону аперіодичної ланки 2-го порядку з передавальної функцією:
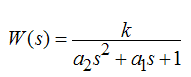
Використавши алгоритм Сімою для визначення параметрів передавальних функцій моделей об'єктів, в результаті отримуємо наступну передавальну функцію:
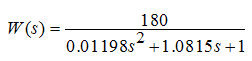
Проведемо моделювання роботи отриманої моделі в програмному пакеті MATLAB і порівняємо отриману криву з вихідною кривою на рисунку 4.2.
Метод площ Сімою є одним з самих найпростіших алгоритмів визначення параметрів передавальних функцій моделей об'єктів по кривій розгону. Однак у силу своєї простоти, дана методика досить часто може давати незадовільні результати — ідентифіковані параметри моделей об'єктів можуть мати велике відхилення в порівнянні з реальними динамічними характеристиками. У зв'язку з цим виникає необхідність у пошуках і синтезі альтернативних методик ідентифікації параметрів ДПТ.
До існуючих альтернативних методів ідентифікації динамічних характеристик відносяться метод Стрейца, графоаналітичний метод, методика Корбіна. Також одним з ефективних методів ідентифікації параметрів ДПТ є використання фільтра Калмана [4], який дозволяє оцінювати вектор стану і параметрів досліджуваної моделі, з використанням низки неповних та зашумлених вимірювань. Всі ці методики вимагають детального дослідження в рамках існуючої системи стабілізації інверсного маятника.
На практиці характеристики двигунів постійного струму однієї і тієї ж моделі можуть відрізнятися. Також можуть відрізнятися криві розгону одного і того ж ДПТ, при обертанні валу в різних напрямках. Для побудови якісної системи управління ці особливості мають бути враховані.
Выводы
Таким чином, в даній роботі була коротко описана модель і конструкція балансуючого робота, проаналізовано принцип побудови системи автоматичного управління, а також проведення ідентифікація залежності зміни швидкості обертання валу двигуна від часу при подачі на двигун постійної напруги.
1. Для найбільш точного розрахунку керуючого впливу та, разом с цим, плавної стабілізації конструкції необхідно враховувати модель двигуна, тобто його передавальні функції при роботі в різних режимах і при обертання в різних напрямках.
2. Для обробки сигналів з датчиків є можливість використовувати комплементарні фільтри або ж фільтр Калмана. Надалі необхідно порівняти ці алгоритми і вибрати найбільш ефективний.
3. Для визначення переміщення конструкції та положення будуть використовуватися вбудовані в двигун енкодери.
На момент написання даного реферату магістерська робота не завершена. Остаточне завершення планується у грудні 2013 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.
Список использованной литературы
- Симою М.П. Определение коэффициентов передаточных функций линеаризованных звеньев систем регулирования. Автоматика и телемеханика, 1957г., №6. С. 514-527
- Льюнг Л. Идентификация систем. Теория для пользователя: М.: Наука, 1991г., 432 с.
- Ерофеев А.А. Теория автоматического управления: Учебник для вузов. – 2-е изд., перераб. и доп. – СПб.: Политехника, 2001. – 302 с.: ил. С. 34
- Эйкхофф П. Основы идентификации систем управления. Оценивание параметров и состояния.–М.: Мир, 1975г., 687 с.
- Голиков В.В. Дипломний проект "Спроектувати систему автоматичного управління балансуючого робота з використанням МЕМ датчиків руху. Спроектувати програмну частину"
- Подлесный Н.И. Элементы систем автоматического управления и контроля / Подлесный Н. И., Рубанов В. Г. — К.: Высшая шк., 1991. — 330 с.
- Башарин А. В. Примеры расчетов автоматизированного электропривода / Башарин А. В., Голубев Ф. Н., Кепперман В. Г. — М.: Энергия, 1964. — 274 с.
- Корнилов Ю. Г. Теоретические основы автоматического регулирования / Корнилов Ю. Г. — К.: Техника, 1965. — 462 с.
- Зайцев Г. Ф. Основы автоматического управления / Зайцев Г. Ф., Костюк З. И., Чинаев П. И. / Изд. 2-е. — К.: Техника, 1977. — 472 с.
- Фритч В. Применение микропроцессоров в системах управления / Фритч В. — М.: Мир, 1984. — 464 с.
- Фридмен М. Проектирование систем с микрокомпьютерами / Фридмен М., Ивенс Л. — М.: Мир, 1986. — 405 с.