Реферат по теме выпускной работы
Содержание
Введение1. Актуальность темы
2. Цель и задачи исследования
3. Краткое описание объекта и системы управления
4. Экспериментальные исследования
Выводы
Список использованной литературы
Введение
На сегодняшний день существует множество реализаций так называемого балансирующего робота. По своей сути балансирующий робот представляет собой систему поддержания равновесия конструкции в виде перевернутого маятника, как правило это платформа на двух колесах. Принципы построения данных систем схожи, однако применяемые алгоритмы стабилизации и электронные средства в реальных моделях существенно различаются. При синтезе системы управления очень важно получить точное математическое описание объекта управления, а также всех компонент входящих в состав системы. Это можно сделать на основе законов физики, механики и т.д. Однако порой знаний об объекте недостаточно или же параметры объекта могут изменятся в некоторых пределах. Тогда прибегают к экспериментальным методам, суть которых сводится к статистической обработке технологических данных. При экспериментально-аналитическом методе априорная модель, полученная аналитическим путем, уточняется в соответствующих экспериментах.
1. Актуальность темы
Вопрос стабилизации физически неустойчивых объектов является одной из самых частых проблем теории автоматического управления, с которой сталкиваются инженеры этой области. Поэтому возникает необходимость получения богатого опыта по решению подобных задач для будущих инженеров. При этом важно получение не только теоретических знаний и навыков работы с математическими моделями, а в первую очередь практических умений и опыта работы с реальными физическими объектами, физическую природу которых невозможно полностью описать с помощью модели.
Параллельно с этим, технический прогресс идет по пути миниатюризации датчиков, исполнительных механизмов, снижения их энергозатрат и стоимости и повышения универсальности, надежности и быстродействия микросхем и микропроцессоров. Это создает возможность создания объектов, которые сочетают в себе все аппаратные средства не только для формирования управляющего воздействия, но и для измерения физических величин обратной связи и реализации сложных систем управления. Возможность полной реализации всех этих функций в середине одного объекта позволяет сделать его автономным и компактным.
Одной из самых распространенных систем динамического равновесия является САУ робота в виде перевернутого маятника. Она уже получила широкое распространение в системах автоматизации и робототехники благодаря своей простоте и высокой маневренности. Использование для этой системы современных микроэлектромеханических систем (МЭМС-датчиков) позволяет получить еще большую миниатюризацию и доступность таких систем, что позволяет расширить область их применения. Для плавной стабилизации требуется очень точное определение угла отклонения и расчет управляющего воздействия с учетом динамических характеристик двигателей постоянного тока, которые приводят балансирующего робота в состояние равновесия. Параметры двигателей могут существенно отличаться даже при направлении вращения вала. Поэтому возникает необходимость идентификации модели двигателя в различных режимах работы с целью дальнейшего учета этой модели в синтезе законов управления.
2. Цель и задачи исследования
Главной целью магистерской работы является проектирование и практическая реализация автоматической системы поддержания динамического равновесия балансирующего робота, выполненного в виде конструкции типа перевернутый маятник
.
Основные задачи работы:
- Анализ существующих систем стабилизации и динамического равновесия.
- Анализ имеющихся методик идентификация моделей подобного типа.
- Разработка математической модели объекта.
- Разработка функциональной и структурной схем объекта.
- Моделирование динамических процессов в объекте.
- Анализ существующих методов определения угла наклона конструкции и обработки показаний с датчиков.
- Исследование методик идентификации положения объекта.
- Синтез алгоритмов идентификации параметров балансирующего робота (параметры двигателя, угол наклона, положение в пространстве).
- Уточнение математической модели и программирование алгоритмов обработки показаний датчиков.
- Разработка стендовой модели балансирующего робота.
3. Краткое описание объекта и системы управления
Конструкция балансирующего робота является довольно простой и именно поэтому имеет ряд полезных свойств. Упрощенная конструкция балансирующего робота изображена на рисунке 3.1. Наличие двух колес уменьшает габариты и повышает надежность, а раздельное управление каждым из них (с помощью двигателей постоянного тока) делает платформу очень маневренной, в частности платформа может поворачивать при движении или выполнять разворот на месте. Но главным недостатком является то, что платформа неустойчива и при выключении двигателей при малейшем возмущении платформа потеряет баланс и упадет. Однако сделать платформу устойчивой призвана система автоматического управления. Создав замкнутый контур, постоянно измеряя угол, имеется возможность вырабатывать управляющие воздействия с большой частотой, всякий раз корректируя положение платформы.
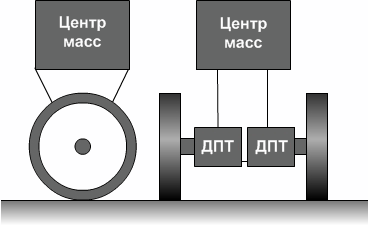
Рисунок 3.1 - Платформа в виде перевернутого маятника
Идея поддержания баланса достаточно проста. Конструкция имеет единственную точку равновесия когда центр масс груза находится непосредственно над осью вращения. Если центр тяжести конструкции отклоняется в сторону, то сила тяжести частично передается через сопротивления к земле, а другая ее составляющая создает момент вращения конструкции, который стремится свергнуть конструкцию на бок. Чтобы компенсировать эту силу, система должна начать движение с ускорением в сторону падения. Сила F, которую создает ускорение также раскладывается на силу действующую в сторону опоры, и силу, которая создает обратный момент вращения конструкции.
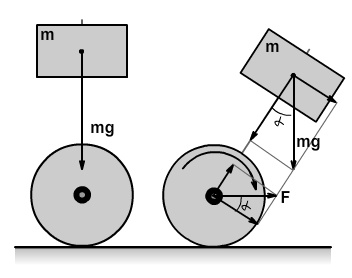
Рисунок 3.2 - Физическая модель объекта
То есть для поддержания баланса необходимо выполнение условия:
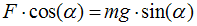
Но если рассматривать только малые отклонения от состояния равновесия (α → 0), то благодаря линеаризации можно получить более простое условие для равновесия:
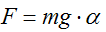
Таким образом процесс поддержания равновесия такой системы можно разделить на две основные составляющие: определение угла наклона конструкции от состояния равновесия и управления вращением колес в зависимости от величины отклонения, для формирования силы, которая компенсирует падение.
Принцип поддержания равновесия можно проиллюстрировать нижеприведенной анимацией.
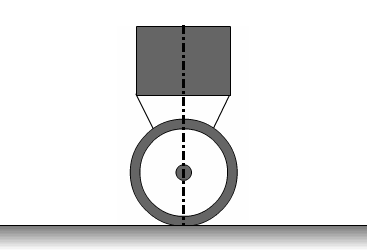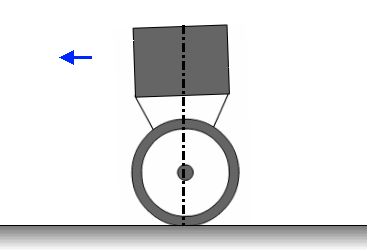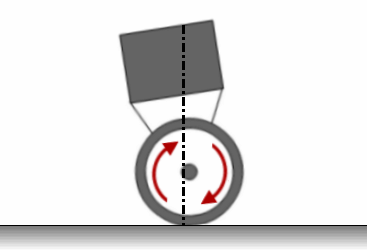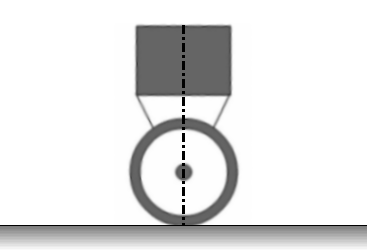
Рисунок 3.3 - Принцип стабилизации объекта. Анимация состоит из 11 кадров с задержкой в 500мс между кадрами. Количество циклов повторения анимации является бесконечным.
Для определения угла отклонения конструкции от нормали к поверхности наиболее правильным будет использование МЭМС, которая представляет собой объединение акселерометра и гироскопа. Обобщенная структурная схема данной системы представлена на рисунке ниже.
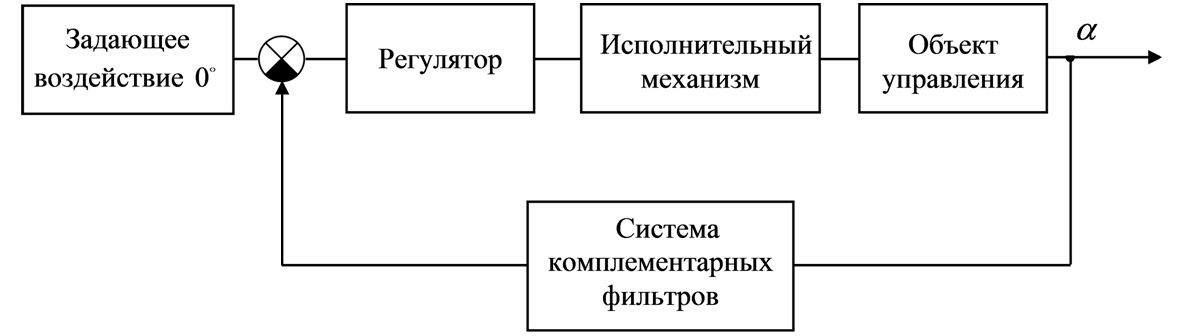
Рисунок 3.4 - Обобщенная структурная схема системы
В качестве объекта управления выступает конструкция перевернутого маятника. Роль исполнительного механизма играет двигатель постоянного тока со встроенным энкодером, в системе присутствуют два двигателя. Задачи регулирования и вычислений управляющий воздействий возложены на микроконтроллер, а закон управления реализуется и задается программно. Оба двигателя постоянного тока управляется с помощью широтно-импульсной модуляции (ШИМ). Микроконтроллер определяет скважность ШИМ сигнала и направление вращения вала и посылает эти сигналы на драйвер двигателя.
Выходом системы является угол отклонения маятника от нормали к поверхности, который измеряется акселерометром и гироскопом. Сигналы с МЭМС пропускаются через систему комплементарных фильтров, которая изображена на рисунке 3.4. Разность задающего воздействия (0 градусов) и текущего угла отклонения поступает на вход регулятора (в нашем случае микроконтроллера), который рассчитывает управляющее воздействие для приведения конструкции в равновесие.
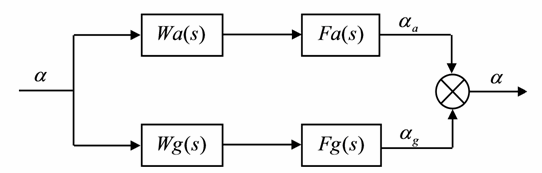
Рисунок 3.5 - Система комплементарных фильтров
где Wa(s) - передаточная функция акселерометра; Wg(s) - передаточная функция гироскопа; Fa(s) - передаточня функция фильтра акселерометра; Fg(s) - передаточная функция фильтра гироскопа;  - измеряемый угол.
- измеряемый угол.
Целью системы комплементарных фильтров является поддержка равенства входного и выходного сигналов. Но на низких частотах изменения угла наклона система отдает предпочтение показаниям акселерометра. Это связано с тем, что когда конструкция находится в состоянии, близком к состоянию покоя, именно данные акселерометра наиболее соответствуют действительности, а на высоких частотах – более точны показания гироскопа, который не чувствителен к резким движениям конструкции. Каждый датчик доминирует
на частоте сигнала, на которой влияние его недостатков является минимальным. Данный подход обеспечивает достаточно высокую точность измерений при относительной простоте реализации. Существуют также альтернативные методы обработки показаний датчиков, например с использованием фильтра Калмана.
4. Экспериментальные исследования
Целью идентификации параметров является получение наиболее точного математического описания системы в целом, а также синтез алгоритмов обработки показаний датчиков и энкодеров для определения таких параметров как угол отклонения маятника от нормали к поверхности, перемещение и текущая координата объекта. Под идентификацией можно понимать как формирование моделей на основе результатов наблюдений, экспериментов и исследование их свойств, так и определение угла отклонения с помощью фильтров и определение перемещения и координаты с помощью встроенных энкодеров [2]. В данном разделе проведена идентификация структуры математической модели двигателя, в частности получено уравнение изменение скорости вращения двигателя при подачи единичного ступенчатого воздействия. Полученная передаточная функция в дальнейшем может быть учтена в синтезе закона регулирования.
Двигатель постоянного тока (ДПТ) независимого возбуждения описывается следующей системой уравнений:
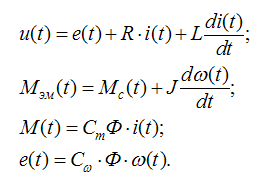
Где u(t) – напряжение на якорной обмотке двигателя; e(t) – э.д.с. якоря; i(t) – ток якоря; Ф – поток, который создается обмоткой возбуждения; Мэм(t) – электромагнитный момент двигателя; Мc(t) – момент сопротивления движения; w(t) – скорость вращения вала двигателя; R – активное сопротивление якорной цепи; L – индуктивное сопротивление якорной цепи; J – суммарный момент инерции якоря и нагрузки; Cw – электромагнитная постоянная двигателя; Cm – механическая постоянная двигателя.
Для создания модели двигателя необходимо получить передаточные функции, применив к дифференциальным уравнениям преобразования Лапласа. Передаточная функция, которая характеризует ток якоря и падения напряжения на якоре:
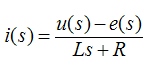
Передаточная функция, которая связывает динамический момент и скорость вращения вала двигателя:
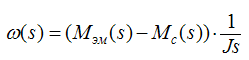
Используя полученные передаточные функции можно составить структурную схему модели двигателя постоянного тока, которая представлена на рисунке 4.1. Поскольку динамические характеристики двигателя заранее не известны, зададимся произвольными данными и выполним моделирование скорости вращения двигателя: L=0,001 Гн, R=61 Ом, CmFi=0,22, J=0,0004 кг*м2.
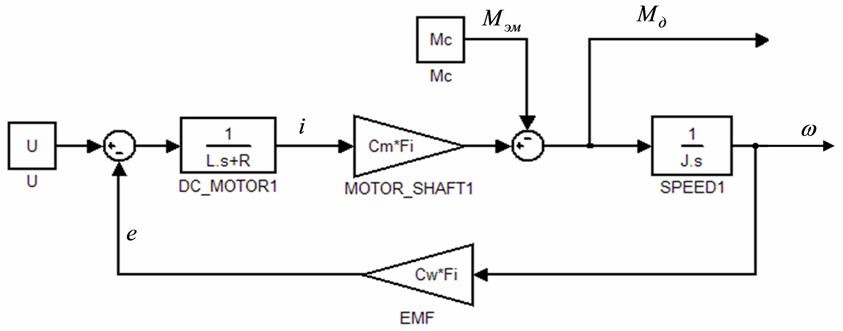
Рисунок 4.1 - Структурная схема двигателя постоянного тока
Промоделировав работу модели с входным воздействием равным 18 вольт был получен график переходного процесса скорости вращения вала двигателя.
Предположив, что кривая разгона на рисунке 4.2 была получена экспериментально, т.е. были обработаны показания встроенного в двигатель энкодера, проведем идентификацию динамических характеристик двигателя методом Симою [1]. Данный метод является одним из наиболее удобных при использовании ЭВМ для идентификации объекта управления в условиях проведения активного эксперимента. Конечную модель объекта будем искать в виде типовой кривой разгона апериодического звена 2-го порядка с передаточной функцией:
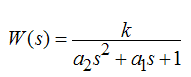
Использовав алгоритм Симою для определения параметров передаточных функций моделей объектов, в результате получаем следующую передаточную функцию:
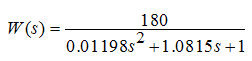
Проведем моделирование работы полученной модели в программном пакете MATLAB и сравним полученную кривую с исходной кривой на рисунке 4.2.
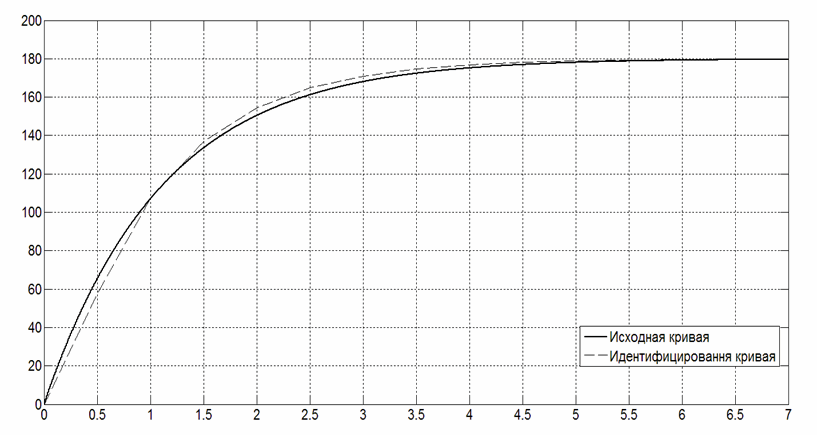
Рисунок 4.3 - Исходная и идентифицированная кривые переходных процессов скорости вращения вала двигателя
Метод площадей Симою является одним из самых простейших алгоритмов определения параметров передаточных функций моделей объектов по кривой разгона. Однако в силу своей простоты, данная методика довольно часто может давать неудовлетворительные результаты – идентифицированные параметры моделей объектов могут иметь большое отклонение в сравнении с реальными динамическими характеристиками. В связи с этим возникает необходимость в поисках и синтезе альтернативных методик идентификации параметров ДПТ.
К существующим альтернативным методам идентификации динамических характеристик относятся метод Стрейца, графоаналитической метод, методика Корбина. Также одним из эффективных методов идентификации параметров ДПТ является использование фильтра Калмана [4], который позволяет оценивать вектор состояния и параметров исследуемой модели, с использованием ряда неполных и зашумленных измерений. Все эти методики требуют детального исследования в рамках существующей системы стабилизации инверсного маятника.
На практике характеристики двигателей постоянного тока одной и той же модели могут отличаться. Также могут отличаться кривые разгона одного и того же ДПТ, при вращении вала в разных направлениях. Для построения качественной системы управления эти особенности должны быть учтены.
Выводы
Таким образом, в данной работе была кратко описана модель и конструкция балансирующего робота, проанализирован принцип построения системы автоматического управления, а также проведения идентификация зависимости изменения скорости вращения вала двигателя от времени при подаче на двигатель постоянного напряжения.
1. Для наиболее точного расчета управляющего воздействия и, следовательно, плавной стабилизация конструкции необходимо учитывать модель двигателя, т.е. его передаточные функции при работе в разных режимах и при вращениях в разных направлениях.
2. Для обработки сигналов с датчиков имеется возможность использовать комплементарные фильтры или же фильтр Калмана. В дальнейшем необходимо сравнить эти алгоритмы и выбрать наиболее эффективный.
3. Для определения перемещения конструкции и текущей координаты на поверхности будут использоваться встроенные в двигатель энкодеры.
На момент написания данного реферата магистерская работа не завершена. Окончательное завершение планируется в декабре 2013 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Список использованной литературы
- Симою М.П. Определение коэффициентов передаточных функций линеаризованных звеньев систем регулирования. Автоматика и телемеханика, 1957г., №6. С. 514-527
- Льюнг Л. Идентификация систем. Теория для пользователя: М.: Наука, 1991г., 432 с.
- Ерофеев А.А. Теория автоматического управления: Учебник для вузов. – 2-е изд., перераб. и доп. – СПб.: Политехника, 2001. – 302 с.: ил. С. 34
- Эйкхофф П. Основы идентификации систем управления. Оценивание параметров и состояния.–М.: Мир, 1975г., 687 с.
- Голиков В.В. Дипломний проект "Спроектувати систему автоматичного управління балансуючого робота з використанням МЕМ датчиків руху. Спроектувати програмну частину"
- Подлесный Н.И. Элементы систем автоматического управления и контроля / Подлесный Н. И., Рубанов В. Г. — К.: Высшая шк., 1991. — 330 с.
- Башарин А. В. Примеры расчетов автоматизированного электропривода / Башарин А. В., Голубев Ф. Н., Кепперман В. Г. — М.: Энергия, 1964. — 274 с.
- Корнилов Ю. Г. Теоретические основы автоматического регулирования / Корнилов Ю. Г. — К.: Техника, 1965. — 462 с.
- Зайцев Г. Ф. Основы автоматического управления / Зайцев Г. Ф., Костюк З. И., Чинаев П. И. / Изд. 2-е. — К.: Техника, 1977. — 472 с.
- Фритч В. Применение микропроцессоров в системах управления / Фритч В. — М.: Мир, 1984. — 464 с.
- Фридмен М. Проектирование систем с микрокомпьютерами / Фридмен М., Ивенс Л. — М.: Мир, 1986. — 405 с.





