Реферат по теме выпускной работы
Содержание
- Введение
- 1. Актуальность темы
- 2. Цель и задачи исследования, планируемые результаты
- 3. Краткий обзор существующих решений
- 4. Основные принципы стабилизации полёта квадрокоптера
- 5. Экспериментальные исследования
- Выводы
- Список источников
Введение.
Новым течением в современном авиамоделизме является построение мультикоптеров – беспилотных летательных аппаратов (БПЛА) с четным количеством роторов, вращающимися диагонально в противоположных направлениях. В случае, когда двигателей четыре, такой БПЛА называется – квадрокоптер. На сегодняшний день главным трэндом является создание небольшого беспилотного квадрокоптера. Основными причинами такого положения вещей являются возможность простого управления и маневренность. Квадрокоптеры имеют большой спрос среди авиамоделистов, но также находят свое применение и в профессиональной сфере, например, полиции или армии. Уже были замечены квадрокоптеры доставляющие почту адресату, их применяют для панорамных съемок важных мероприятий.
1. Актуальность.
Необходимость стабилизации полёта квадрокоптера вытекает из принципа его работы. Например, стабильность полёта планера или самолета обусловлена их устойчивостью, т.е. возможность восстанавливать без вмешательства пилота кинематические параметры невозмущенного движения и возвращаться к исходному режиму полёта после прекращения действия возмущений. Квадрокоптер же таким свойством не обладает и при малейшем внешнем воздействии начинается «неуправляемое снижение».
2. Цель и задачи исследования, планируемые результаты.
Цель работы – разработать и исследовать электронную систему стабилизации полёта квадрокоптера.
Основные задачи исследования:
- Анализ методов стабилизации полёта квадрокоптера.
- Исследование и выбор инерциальных датчиков.
- Анализ имеющихся методов обработки данных, полученых с инерциальных датчиков.
- Создание алгоритма стабилизации на основании данных исследований.
- Разработка стендовой модели квадрокоптера.
Объект исследования: беспилотный летательный аппарат – квадрокоптер.
Предмет исследования: определение абсолютного положения летательного аппарата в пространстве (углы наклона, высота, линейные перемещения).
3. Краткий обзор существующих решений.
Абсолютно во всех источниках указывается, что минимальный набор датчиков для квадрокоптера это: гироскоп, акселерометр и магнитометр. Для некоторых задач необходимо точно поддерживать высоту полёта аппарата и отслеживать траекторию полёта [1]. В таких случаях в довесок к вышеперечисленным датчикам добавляются блоки с высотомером и GPS.
Для корректировки полученных значений угла с гироскопа, существует несколько путей решения, например использование ПИД-регулятора [2] или комплементарного фильтра [3]. Также данные можно фильтровать с помощью фильтра Калмана [4]. Самым популярным всеже является использование комплементарного фильтра, ввиду своей простоты.
Важным вопросом при стабилизации полёта квадрокоптера является сохранение данных о текущем абсолютном положении аппарата в пространстве. Для этого пользуются матрицей поворота, уравнениями Лагранжа или кватерионами [5].
4. Основные принципы стабилизации полёта квадрокоптера
Для того чтобы эффективно стабилизировать квадрокоптер в полете необходимо:
- Иметь возможность определения, в каком состоянии находится система в данный момент.
- Иметь возможность оказывать управляющие воздействия на систему.
- Знать, в каком состоянии будет поддерживаться система.
Для определения состояния системы используют различные датчики (гироскоп, акселерометр, магнитометр, высотомер и т.д.) обеспечивающие обратную связь. Управляющее воздействие оказывают посредством изменения скорости вращения двигателей. Например, если БПЛА наклонился на левый бок, то соответственно необходимо увеличить обороты левого двигателя и уменьшить обороты правого.
В первую очередь для стабилизации квадрокоптера, необходимо знать его абсолютное положение в пространстве. Стабилизация осуществляется по ряду параметрам: высоте, углам, линейным перемещениям. Так как квадрокоптер является летательным аппаратом, для углов наклона используются авиационные термины: тангаж (в плоскости оси Х), крен (в плоскости оси У) и рыскание (в плоскости оси Z, рис. 1).

Рисунок 1 — Анимация процесса поворота относительно оси Z (рыскание). Основные параметры анимации: количество кадров — 6; объем — 157 КВ; количество циклов повторения — 7
Самым рациональным решение для квадрокоптера, будет использование микроэлектромеханических (MEMS) датчиков. Они имеют малые массогабаритные показатели, высокое быстродействие, функциональность и надежность, но и имеют ряд недостатков, таких как зависимость показаний от температуры, дрейф нуля, чувствительность к вибрациям.
Для определения крена, тангажа и рыскания воспользуемся гироскопом, являющимся датчиком моментальных угловых скоростей вокруг оси. Для определения угла с помощью гироскопа необходимо интегрировать его показания, например методом прямоугольников [6]:
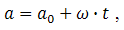
где α – текущее значение угла, α0 – предыдущее значение угла, ω – текущее значение угловой скорости, t – время между измерениями.
Т.е. гироскоп опрашивается постоянно с временным интервалом t, получаем моментальное значение угловой скорости ω и вычисляем текущее значение угла (a) прибавив к предыдущему значению угла (a0) приращение за данный промежуток времени. Но при таком подходе вместе с приращением постоянно суммируется и ошибка, вызванная погрешностью гироскопа. Это приведет к тому, что с течением времени вычисленное значение угла будет все дальше и дальше уходить от реального значения (см. рис. 2).
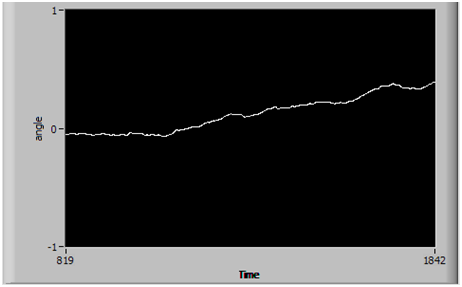
Рисунок 2 – Показания гироскопа в состоянии покоя
При этом сами показания гироскопа имеют большой разброс, поэтому рекомендуется применять усреднение показаний, например методом скользящего среднего. В данном алгоритме использовалось усреднение по 5 точкам. Если увеличить количество точек, то система может реагировать на изменение угла с запаздыванием. Поэтому рекомендованное количество точек не больше 10.
Ввиду вышеперечисленного, периодически необходимо корректировать значения вычисленных углов. Для такой корректировки используется акселерометр, измеряющий проекцию кажущегося ускорения на чувствительную ось. Иными словами на выходе акселерометра мы имеем значение суммы проекции ускорения свободного падения (G) и проекции абсолютного ускорения объекта на чувствительную ось (Рис. 3).
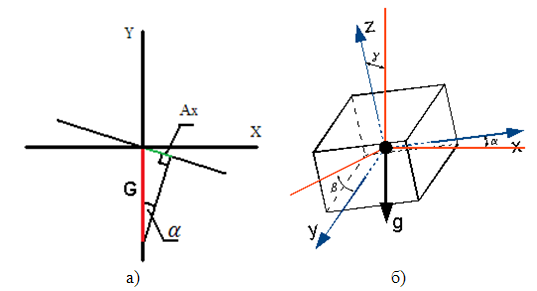
Рисунок 3 – Определение углов крена, тангажа и рыскания акселерометром: а) одноосевой случай; б) трехосевой случай.
Если система находится в статическом положении или движется с постоянной скоростью (собственное ускорение равно нулю), то углы наклона рассчитывается по следующим формулам (для трехосевого случая):
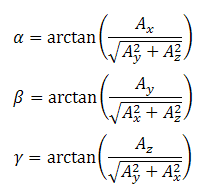
Для одноосевого случая:
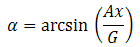
Здесь Ax, Ay, Az – проекции вектора ускорения свободного падения на оси X, Y, Z соответственно. Как известно, тангенс дает углы от -90 до 90 градусов. Для получения всех 360, используют функцию atan2.
Но акселерометр выдает точные значения только в состоянии покоя. В движении к показаниям прибавляется проекция вектора собственного ускорения и значение угла «уплывает». Именно поэтому в такой динамичной системе как квадрокоптер, акселерометр используется лишь для коррекции значений углов. Также отсюда вытекает еще одна особенность. Используя лишь акселерометр, скорректировать возможно лишь углы крена и тангажа (выровнять относительно горизонта). Но скорректировать угол рыскания не представляется возможным из-за совпадения оси вращения с вектором G. Для решения этой проблемы используют магнитометр (цифровой компас), который вводит еще один вектор в систему [7]. Магнитометр же имеет свои недостатки, основной из которых – низкая точность. Погрешность может достигать 5 градусов, а рядом с двигателями квадрокоптера и силовых линий питания эта погрешность только возрастет.
Также важным элементом стабилизации полёта квадрокоптера является высотомер, необходимый для удержания необходимой высоты и безопасной посадки в автоматическом режиме. Ультразвуковые высотомеры рационально использовать на относительно малых высотах (до 4 метров), для больших высот используются лазерные высотомеры или высотомеры на бародатчике. Высокой точности от такой системы не требуется, приемлемой является погрешность в 1 сантиметр. Квадрокоптер весьма динамичная система, что обуславливает высокие требования к быстродействию. Время измерения не должно превышать 0.1 секунды.
В качестве отправной точки при разработке использована публикация [8] с описанием самодельного ультразвукового дальномера.
В высотомере реализован времяпролетный метод, основанный на измерении времени прохода акустических колебаний от измерителя до объекта и обратно [9]. Устройство работает по следующему обобщенному алгоритму:
- Передающая часть формирует и излучает пакет импульсов ультразвуковой частоты (частота зависит от модели излучателя и приемника).
- Приемная часть принимает и усиливает отраженный сигнал.
- Схема обработки фиксирует максимум полученного сигнала. Время между отправкой импульсов и возвращением максимума будет пропорционально расстоянию.
Функциональная схема высотомера представлена на рисунке 4. Микроконтроллер (МК) с помощью таймера формирует пакет из 8 импульсов (оптимальное количество установлено экспериментально) частотой 38 кГц. Слабый отраженный сигнал усиливается электронным усилителем. Коэффициент усиления усилителя по напряжению подобран опытным путем и равен 400. При меньших значениях коэффициента падает максимальное измеряемое расстояние до объекта, при больших – усилитель входит в ограничение на малых дистанциях до объекта. Усиленный измерительный сигнал детектируется и с помощью аналого-цифрового преобразователя (АЦП) преобразуется в дискретный массив цифровых значений, расположенный в памяти МК. В завершении цикла измерений МК находит максимальный элемент массива и по его индексу рассчитывает дистанцию до объекта.
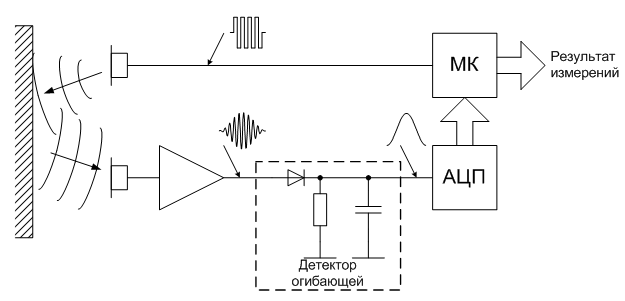
Рисунок 4 – Функциональная схема высотомера
Разрешающая способность высотомера определяется как отношение предела измерений к числу ячеек измерительного массива. Таким образом, для обеспечения разрешения в 1 см при пределе в 4 м объем ОЗУ должен быть не менее 400 байт. При этом время преобразования АЦП не должно превышать 62 мкс (25 мс/400).
При создании опытного образца высотомера был использован доступный и недорогой микроконтроллер ATmega8 (ценой в $1), содержащий АЦП с минимальным временем преобразования 15 мкс и объемом ОЗУ 1024 байта, что позволило обеспечить разрешающую способность на уровне 0,4 см.
5. Экспериментальные исследования.
Для корректировки углов воспользуемся комплементарным фильтром, работа которого описывается следующим выражением:
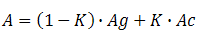
Здесь Ac и Ag значения угла наклона, полученные при помощи акселерометра и гироскопа соответственно, A – значение скорректированного угла, K – коэффициент фильтра. Как видно, итоговая величина угла наклона представляет собой сумму интегрированного значения гироскопа и мгновенного значения акселерометра. По сути, главная задача комплементарного фильтра заключается в том, чтобы нивелировать дрейф нуля гироскопа и ошибки интегрирования. Вес корректирующих значений определяется коэффициентом фильтра K.
Выбор коэффициента K зависит от величины дрейфа нуля гироскопа и от скорости накопления ошибок вычисления. Так, слишком большое значение коэффициента приведет к тому, что на результат работы фильтра будет сильно влиять вибрация корпуса квадрокоптера. Слишком же малое, может оказаться недостаточным для ликвидации дрейфа нуля гироскопа. Как правило, коэффициент фильтрации K подбирается при настройке для каждого инклинометра исходя из вышеуказанных условий. Типичное значение лежит в диапазоне от 0,05 до 0,15. В данной системе был задан коэффициент фильтрации K комплементарного фильтра равным 0,1.
На рисунке 5 приведен результат работы фильтра для оси Х. Как видно, систему сначала повернули на 26 градусов, затем еще на 6.
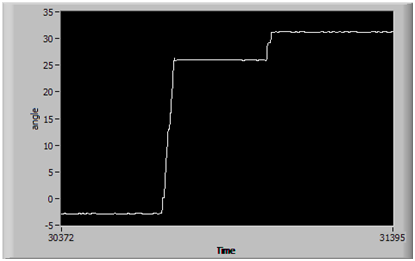
Рисунок 5 – Результат работы комплементарного фильтра
Погрешность отфильтрованного значения угла (Рис. 6) составляет ±0,05°, что является отличным результатом для задачи стабилизации полёта квадрокоптера.
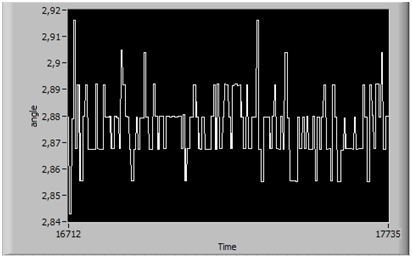
Рисунок 6 – Результат работы комплементарного фильтра в состоянии покоя
Выводы
- Для стабилизации полёта квадрокоптера необходимо знать его абсолютное положение в пространстве, в особенности углы крена, тангажа и рыскания.
- Для определения углов, одного гироскопа не достаточно. Для получения точных данных необходимо вводить коррекцию с помощью акселерометра и магнитометра.
- Использование комплементарного фильтра имеет высокую эффективность, при этом не затрачивает много машинных ресурсов.
При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2013 года.
Список использованной литературы
1. Система управления БПЛА для полета на
малых высотах/ Т.В. Белоцерковский – Национальный
технический университет Украины.
2. Building and controlling the Quadrocopter – Pavel
Chmelar – Number 5, Volume VI, December 2011.
3. Design and control of quadrotors with application to autonomous
flying – Samir BOUABDALLAH – ingenieur d'etat,
Universite Aboubekr Belkaid, Tlemcen, Algerie
de nationalite algerienne
4. An Introduction to the Kalman Filter – Greg Welch, Gary
Bishop – Department of Computer Science. University of North
Carolina at Chapel Hill Chapel Hill, NC 27599–3175 Updated:
Monday, July 24, 2006.
5. Разработка управляющих программ промышленных роботов/ А.С. Климчик
Р.И. Гомолицкий Ф.В. Фурман К.И. Сёмкин - Курс лекций для
студентов – C. 131
6. Самарский А.А., Гулин А.В. Численные методы: Учеб. пособие для
вузов. – М.: Наука. Гл. ред. физ-мат. лит., 1989. – 432 с.
7. Основы построения бесплатформенных инерциальных систем/ В.В.Матвеев,
В.Я.Располов – СПб.: ГНЦ РФ ОАО «Концерн «ЦНИИ
«Электроприбор», 2009. – 280 с.
8. Ampersant [Электронный ресурс]: Ультразвуковой дальномер –
Электронные данные. – Режим
доступа:http://www.ampersant.ru/ultra/Дата доступа: апрель 2013.
– Загл. с экрана.
9. Разработка ультразвукового измерителя дальности / А.В. Бурдуков //
Дипломный проект Государственный университет аэрокосмического
приборостроения. – 2010. – С. 17 – 22.
10. Strapdown inertial navigation system. Part 1 –
Navigation equations – Albert Ortyl, Zdzislaw
Gosiewski – Journal of thheoretical and applied
mechanics – 1,36,1998 – C.83 – 96.
