Назад в библиотеку

---

Метод побудови найкоротших шляхів у дворівневому графі

Автори: Г.В. Білик, І.С. Грунський, Н.В. Ногіна
Джерело: Информационно-управляющие системы и компьютерный мониторинг / Материалы IV международной научно-технической конференции студентов, аспирантов и молодых ученых. –  Донецк, ДонНТУ – 2013, секция 8 [Перейти]

  Анотація

    Білик А.В., Грунський І.С., Ногіна Н.В. Метод побудови найкоротших шляхів у дворівневому графі. Запропоновано новий метод пошуку найкоротших шляхів у дворівневому графі з поміченими вершинами і дугами.

   Загальна постановка проблеми

Проблема пошуку найкоротших шляхів у графі є загально відомою та важливою для різних застосовань. Існує ряд алгоритмів для вирішення цієї задачі. В останній час ця проблема інтенсивно вивчається для графів складної багаторівневої структури. У даній роботі розглядається задача пошуку найкоротших шляхів у поміченому дворівневому графі від початкової вершини до деякої фінальної.

Актуальність проблеми для таких складних графів полягає в тому, що в прикладних задачах найкоротші шляхи потрібно знаходити для перевезень, які проходять через шляхи, міста, складні транспортні розв’язки. Тому тематика даної роботи достатньо актуальна.

   Мета статті

Розробити метод пошуку найкоротших шляхів у дворівневому графі з поміченими вершинами і дугами, який дозволяв би знаходити помітки найкоротших шляхів та якість цих шляхів.

   Постановка задачі

Розглядаються зв'язні неорграфи [2] зі скінченими множинами вершин Q і ребер E, що не мають петель. Ребро – це є пара вершин (q, u). Ребра графа G відмічено мітками з множини Y, виділено початкову вершину та множину фінальних вершин. Таким чином, G=(Q, E, Y, ρ, q₀, F), де:

Q – скінченна множина вершин графа G ;

E – множина ребер графа G;

Y – множина поміток ребер графа G;

ρ: E→Y – функція розмітки ребер графа G;

q₀ – початкова вершина графа G;

F–множина фінальних вершин графа G.

Граф G будемо називати графом першого рівня. Кожна вершина q графа G є графом G_i – графом другого рівня без петель і кратних дуг, в якому вершини і ребра відмічено мітками з множин M і P відповідно. Так, G_i =(T_i, D_i, M_i, P_i, µ , t,  n₀, f_i), де:

T_i – скінченна множина вершин графа G_i;

D_i – множина дуг графа G_i;

M_i – множина поміток вершин графа G_i; 

P_i – множина поміток дуг графа G_i;

µ: T→M – функція розмітки вершин графа G_i;

t: D→P –  функція розмітки дуг графа G_i;

n₀ – початкова вершина графа G_i;

f_i – фінальна вершина графа G_i.

Вершина графа G_i  має наступний вигляд: (q_i; t_j), де  q_i  – номер вершини  графа G, а  t_j – номер вершини графа G_i. Дуга графа G з¢єднує унікальну пару вершин різних графів G_i.

Кожній вершині q_i графа G поставимо у відповідність число Z(q_i) – якість цієї вершини.

Шляхом у графі G назвемо скінченну послідовність l = q₁ e₁ q₂ e₂…e_k-1 q_k, де q_k з Q, а e_i – дуга, початком якої є вершина q_i, а кінцем – q_i+1.

Шляхом у графі G_i. назвемо скінченну послідовність s = (q₁; t_i) d₁ (q₂; t_j)d₂…d_k-1(q_k; t_n), де (q_i; t_j) з T_i, а d_i – дуга, початком якої є вершина (q_i; t_j), а кінцем – (q_i+1; t_n).

Відмітка шляху s – це послідовність відміток w(s)=m₁ p₁ m₂ p₂…p_k-1 m_k, де m_i= µ(T_i), p_i =t (d_i).

Генеральним шляхом назвемо послідовність I= (q₁; t_i) x₁ (q₂; t_j)x₂…x_k-1(q_k; t_n), де (q_i; t_j) з T_i, а x_i  може бути дугою e_i графа G або дугою d_i графа G_i.

Відмітка шляху I – це послідовність відміток w(I)=a₁ b₁ a₂ b₂…b_k-1 a_k, де a_i= µ(T_i), b_i = ρ(e_i) або b_i = t (d_i).

Вагою генерального шляху I між вершинами q_i та q_j, будемо називати вагу шляху між вершинами (q_i; t_n)та (q_j; t_m) і визначимо її величину за наступною формулою на рисунку 1.1.

                                                                                   

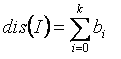
                                                                                  Рисунок  1.1 – Формула ваги генерального шляху

Якість генерального шляху I визначимо через величину dis (I) за  формулою на рисунку 1.2.

                                                                     

                                                                     Рисунок  1.2 – Формула якості генерального шляху                                               

 

Для вершини q_i визначимо множину Pre(q_i) = (q_j | (q_j, q_i)=e_i) та множину Post(q_i) = (q_j | (q_i, q_j)=e_i).

Визначимо операцію з'єднування поміток різних дуг і шляхів. Коли з'єднуються помітки різних дуг, то між ним ставиться оператор об'еднання «W», який у подальшому замінюється відповідно правилам:

а) якщо оператор «W» з'єднує помітки двох однакових вершин: (q_i,t_n)x_w(q_j,t_m)W(q_j,t_m)x_v (q_k,t_p), то замінюємо ці помітки разом з оператором на одну помітку: (q_i,t_n) x_w (q_j,t_m) x_v (q_k,t_p);

б) якщо оператор «W» з'єднує помітки двох різних вершин: (q_i,t_n)x_w (q_j,t_m)W(q_k,t_m), але існує дуга або шлях між цими вершинами: (q_j,t_m)x_v (q_k,t_m), то замінюємо ці помітки разом з оператором на помітку знайденої дуги або шляху: (q_i,t_n) x_w (q_j,t_m)x_v(q_k,t_m);

в) якщо пункти а або б не виконуються, то операція з'єднування не можлива.

   Алгоритм

Вхідні дані: помічений дворівневий граф G з початковою і множиною фінальних вершин.

Вихідні дані: одна або декілька поміток найкоротших шляхів, якість цих шляхів.

Крок 1.

1.1)  Для неорієнтованих графів G для кожного ребра між парою вершин q_i та q_j вводиться дві дуги: (q_i,q_j) та (q_j,q_i).

1.2)  У список вершин графа G вводиться фіктивна кінцева вершина fin, а в список дуг – дуга з кожної фінальної вершини q_i у вершину fin. Ця дуга позначається відміткою µ(q_i;t_j).

1.3)  Створюємо представлення графа G у вигляді списку дуг з їх відмітками і вагою, при цьому відмітки відповідних вершин графів G_i. переносяться на дуги графа G (наприклад, якщо помітками двох вершин і дуги між ними будуть відповідно (q_i,t_n),(q_j,t_m) та x_w, то після перенесення поміток вершин на дугу, помітка дуги матиме наступний вигляд: (q_i,t_n) x_w (q_j,t_m)).

1.4)  Для кожного ребра графа G_i між парою вершин (q_i; t_n) та (q_j; t_m) вводиться дві дуги: ((q_i; t_n);(q_j; t_m)) та ((q_j; t_m);((q_i; t_n)), при цьому відмітки вершин переносяться на дуги.

Крок 2. If в графі G існує хоч одна  вершина, що не є початковою або фінальною, з якої виходить хоч одна дуга в фінальну, then go to Крок 3, else go to Крок 7.

Крок 3. Вибираємо q_i =Pre(fin); q:= q_i.

Крок 4. If q ≠ q₀ then видаляємо вершину q та усі вхідні та вихідні з неї дуги. If при цьому є деякий шлях q_i e_k q e q_j, де q_i Pre(q) та q_j = Post(q), then у граф додається дуга (q_{i ,}q_j) з відміткою e_kW e, отриманою за допомогою операції  з'єднування.

Else, якщо q = q₀ go to Крок 2.

Крок 5. Видаляємо ті петлі, в помітках яких початок і кінець співпадає.

Крок 6. Заміна оператора з'єднування.

На кроках 4 – 6 відбувається видалення однієї вершини.

Для вершин, помітки яких з'єднані оператором «W» (наприклад, (q_i; t_n)W(q_i; t_m)) працює алгоритм [5], який шукає оптимальний шлях між цими вершинами (наприклад, між t_n і t_m, де t_n – визначимо як початкову вершину, а t_m – як фінальну). Для цього створюємо представлення відповідного графа G_i ( t_n, t_m Î G_i) у вигляді списку дуг з їх відмітками і вагою.

If в результаті роботи алгоритму [5] оптимальний шлях знайдено, then поміткою цього шляху замінюємо оператор «W» разом з двома помітками, які він з'єднує.

If оптимальних шляхів декілька, then в список дуг графа G додається така ж сама дуга, але, відповідно, з іншою поміткою.

Else, якщо шляху не існує, then видаляємо дугу (q_{i ,}q_j).

Крок 7. Видаляємо усі вершини, що не є початковою або фінальною та усі вхідні та вихідні з них дуги. В результаті одержуємо граф, що складається лише з двох вершин: початкової та фінальної.

Обчислюємо якість шляху QPath для усіх дуг графа G, які з'єднують ці вершини. Оберемо найменше значення QPath, яке і визначає оптимальний шлях у графі. Якщо найменших значень QPath декілька, то результатом буде декілька шляхів з цими значеннями.

    Висновки

Запропоновано новий метод пошуку найкоротших шляхів у дворівневому графі з поміченими вершинами і дугами, який працює з дворівневим графом G без необхідності приводити його до стандартного вигляду однорівневого графа, але при цьому використовується метод локальної редукції графа.

В результаті застосування методу отримуємо одну або декілька поміток для оптимальних  шляхів і якість цих шляхів у графі G.

Легко бачити, що у випадку, коли всі графи G_i мають по одній вершині, розроблений метод співпадає з раніше розробленим алгоритмом пошуку найкоротшого шляху у поміченому графі методом локальної редукції графа [5]. Таким чином, запропонований метод є суттєвим узагальненням раніше розробленого алгоритму. Узагальнення полягає у наступному.

1)  Кожна вершина графа G є графом G_i.

2)  Проводиться обчислення якості шляху з урахуванням ваги помітки кожної вершини у цьому шляху та помітки ваги кожного ребра у той час, як у [5] виконується тільки обчислення ваги  позначок ребер у шляху.

Використовується алгоритм [5] для графів G_i.

  Список використаної літератури

1. Ногина Н.В. Синтез регулярного выражения языка, порожденного помеченным графом, методом его локальной редукции / Н.В. Ногина,  И.С. Грунский // Искусственный интеллект. – 2012. – №3. – С. 348-353.

2.     Кристофидес, Н. Теория графов: алгоритмический подход / Н. Кристофидес. — М.: Мир, 1978. — 430 с.

3.   Ахо А. Построение и анализ вычислительных алгоритмов / А. Ахо, Дж. Хопкрофт, Дж. Ульман. – М.: Мир, 1979. – 536 с.

4.  Батищев Д.И. Многоуровневая декомпозиция гиперграфовых структур / Батищев Д.И., Старостин Н.В., Филимонов А.В. // Прилож. к журналу «Информационные технологии» №5(141). – М.: Новые технологии. – 2008. – 32 с.

5.     Ногина Н.В. Построение кратчайшего пути в помеченном графе при помощи локальной редукции графа / Н.В. Ногина, А.В. Билык // Сучасна інформаційна Україна: інформатика, економіка, філософія:  матеріали доповідей конференції, 26 квітня 2012 року. – Донецьк, 2012. – 316 с. – С. 76-79.