ДонНТУ   Портал магістрів

Реферат за темою випускної роботи

         

Зміст

Вступ

В області управління технічними системами нечітке моделювання дозволяє отримувати більш адекватні результати в порівнянні з результатами, які грунтуються на використанні традиційних аналітичних моделей і алгоритмів управління. Діапазон застосування нечітких методів з кожним роком розширюється, охоплюючи такі області, як проектування промислових роботів і побутових електроприладів, управління доменними печами і рухом поїздів метро, ​​автоматичне розпізнавання мови і зображень.

Нечітка логіка, яка служить основою для реалізації методів нечіткого управління, більш природно описує характер людського мислення і хід його міркувань, ніж традиційні формально логічні системи. Саме тому вивчення та використання математичних засобів для подання нечіткої вихідної інформації дозволяє будувати моделі, які найбільш адекватно відображають різні аспекти невизначеності, постійно присутньої в навколишньому нас реальності.

Обробка нечіткої інформації і нечіткий висновок давно застосовуються в різних інтелектуальних системах, однак найбільш широке поширення нечіткі системи отримали в галузі управління.

У класичних нечітких регуляторах не передбачені механізми адаптації в реальному часі до мінливих характеристикам взаємодії об'єкта управління з навколишнім середовищем, що не дозволяє застосовувати нечіткі системи для управління об'єктами із змінним в часі властивостями. Однак існує ряд методів, що розширюють можливості нечітких регуляторів у цій галузі.

1. Актуальність теми

Обробка нечіткої інформації і нечіткий висновок давно застосовуються в різних інтелектуальних системах, однак найбільш широке поширення нечіткі системи отримали в галузі управління. Для управління погано формалізуються об'єктами зі складною взаємозв'язком керуючих змінних запропоновано використовувати метод на основі функцій приналежності термів декількох аргументів. Для практичного використання методу актуальне створення спеціалізованого програмного забезпечення.

2. Мета і задачі дослідження та заплановані результати

Метою дослідження є розробка та аналіз алгоритмів нечіткого управління на основі функцій приналежності декількох змінних.

Основні задачі дослідження:

  1. Огляд існуючих методів нечіткого управління на основі функцій приналежності одного аргументу.
  2. Огляд існуючих методів нечіткого управління на основі функцій приналежності кількох аргументів.
  3. Дослідження інформаційних технологій реалізації нечіткого управління.
          Плановані результати: реалізація програмного забезпечення з рішенням методу нечіткого управління на основі функцій приналежності              кількох аргументів

3. Огляд існуючих методів нечіткого управління на основі функцій приладдя декількох аргументів

Адаптація методу Мамдані до використання функцій належності декількох змінних

Методика побудови нечіткого регулятора на основі термів з функціями приналежності кількох аргументів представлена ​​на малюнку 3.1. Побудова нечіткого регулятора включає в себе наступну послідовність дій:

  1. Постановка завдання нечіткого управління;
  2. Формування термів та їх функцій належності;
  3. Формування бази правил системи нечіткого виводу;
  4. Фазифікації вхідних змінних;
  5. Агрегування підумови в нечітких правилах продукцій;
  6. Активізація подзаключеній в нечітких правилах продукцій;
  7. Акумулювання висновків нечтких правил продукцій;
  8. Дефаззіфікації вихідних зміних.

У рамках постановки завдання визначаються вхідні і вихідні змінні об'єкта управління, на основі вхідних змінних вибираються управляючі змінні. Виділені величини представляються у вигляді лінгвістичних змінних.

Для кожної з лінгвістичних змінних формуються терм-множини у вигляді нечітких змінних [1]. Якщо лінгвістична змінна має простою структурою, то для неї можуть бути обрані терми у вигляді нечітких змінних з одновимірної функцією приналежності. Інакше рекомендується використовувати нечіткі змінні з багатовимірними функціями належності. До формування назв термів та їх функцій належності можуть бути залучені експерти. Крім цього, для визначення числа термів та виду їх функцій належності можуть бути використані методи нечіткого кластерного аналізу. Надалі для побудови багатовимірних функцій приналежності в роботі використовується метод нечітких с-середніх.

Методика побудови нечіткого регулятора на основі багатовимірних функцій належності

Рисунок 3.1 – Методика побудови нечіткого регулятора на основі багатовимірних функцій належності

База правил системи нечіткого висновку формується на основі емпіричних знань або знань експертів в проблемній області і представляється у вигляді нечітких продукцій [2]: P = {R1, R2, ...,Rp} – множина правил нечітких продукцій; B = {B1, B2, ...,Bm} – множина вхідних лінгвістичних змінних; W = {W1, W2, ...,Wz} – множина вихідних лінгвістичних змінних.

Правило Rr: Якщо  ПУlkir то  ПУzbjr
ПЗjr : B1  є Btlk,

где Btlk – К-тий терм вхідний лінгвістичної змінної Bl;
Sir – ступінь істинності підумови ПУlkir.

ПЗjr : Wz  є Wtzb,

где Wtzb – b-тий терм вихідної лінгвістичної змінної Wz,

Zir – ступінь істинності підумови ПУlkir

Процедура фаззифікація полягає у встановленні відповідності між конкретним значенням окремої вхідної змінної системи нечіткого виводу і значенням Sir функції приналежності відповідного їй терма вхідний лінгвістичної змінної, яка, у разі багатовимірних функцій, розраховується за формулою багатовимірної табличній інтерполяції (поліномами Ерміта) [3]:

  Sir – µlk (ẍl),

де ẍl – значення вхідної змінної системи нечіткого висновку;

µlk (ẍl) – функція приналежності к-го терма, що входить до підумови ПУlkir.

Агрегування являє собою процедуру визначення ступеня істинності умов по кожному з правил системи нечіткого виводу. Якщо умова правила задано у формі нечітких лінгвістичних висловлювань виду «β є α», етап їх агрегування залишає ступеня істинності без зміни. Якщо ж умова складається з декількох підумови, причому лінгвістичні змінні в підумови попарно не рівні один одному, то визначається ступінь істинності складного висловлювання на основі відомих значень істинності підумови. При цьому для визначення результату використовується формула:

 Sr = min Sir

На етапі агрегування знаходяться всі значення Sr  для кожного з правил, що входять у розглянуту базу правил системи нечіткого виводу.

На етапі активізації для кожної з вихідних лінгвістичних змінних, що входять в окремі подзаключенія правил нечітких продукцій, визначаються функції належності нечітких множин їх значень [4].

Розрахунок значення функції приналежності кожного з подзаключеній для розглянутих вихідних лінгвістичних змінних здійснюється за формулою:

µlk (ÿz) = min {Zzbjr, µlzb (ÿz)},

де µlk (ÿz) – функція приналежності b-того терма;

Zir – ступінь істинності кожного з подзаключеній, що розраховується за формулою:

 Zjr = Sr * Kr,

де Kr – ваговий коефіцієнт правила.

Етап акумуляції полягає в тому, щоб об'єднати або акумулювати з використанням операції max-диз'юнкції всі ступені істинності висновків для отримання функції приналежності кожної з вихідних змінних:

µlk *(ÿz) = (All) µzbr (ÿz),

Дефаззіфікації полягає в тому, щоб, використовуючи результати акумуляції всіх вихідних лінгвістичних змінних, отримати звичайне кількісне значення кожної з вихідних змінних, яке може бути використане спеціальними пристроями, зовнішніми по відношенню до системи нечіткого виводу. Для одновимірних функцій належності застосовується стандартний метод центру тяжіння. Для багатовимірного випадку використовується узагальнення метод центру ваги:

yzn*  = 1/Vz (int) yzn * µlk *(ÿz) dv,

де yzn*  – результат дефаззіфікації;

Vz – обсяг фігури, утвореної функцією приналежності µlk *(ÿz).

Нечіткий висновок, заснований на нейронної мережі

Дуже часто робиться припущення, що вхідні змінні незалежні один від одного [5]. Це обумовлює поділ на класи, иллюстрируемое на малюнку 3.2.

Класичне поділ вхідного простору на області  

Рисунок 3.2 – Класичне поділ вхідного простору на області  

Біле поле означає приналежність до даного класу, сіре поле – часткову приналежність до кожного з сусідами класів (або відсутність приналежності до класу).

При такому підході кожна вхідна змінна має власні вхідні множини. Вони утримуються в умовах правил у вигляді:

IF (X1 это A1k AND ... AND Xn это Ank ),


 де X1,…,Xn – вхідні змінні (n – кількість входів), а A1k,…,Ank – це нечіткі множини, що містяться в умові k-го правила (k=1,2,…,N; N – кількість правил). Наприклад, для малюнка 2.2 можна виписати наступні умови правил:

R1 : IF (X1 це НЕГАТИВНО AND X2 це ВЕЛИКЕ),

R2 : IF (X1 це НЕГАТИВНОЕ AND X2 це МАЛЕ),

R3: IF (X1 це ПОЗИТИВНА).  

 Символи, позначають тут відповідні області, показані на малюнку 3.3. Для деяких додатків такий підхід являє собою серйозне обмеження, оскільки не завжди вхідні змінні є взаємно незалежними. На малюнку 3.3 представлений приклад поділу простору вхідних станів вельми тривіальної завдання:

R1 : IF (X1 < X2),

R2 : IF (X1 ≈ X2),

        R3: IF (X1 > X2), 


для якої класичний підхід виявляється не самим доцільним.

 Пропоноване поділ вхідного простору на класи

Рисунок 3.3 – Пропоноване поділ вхідного простору на класи

 

В якості вирішення можна запропонувати заміну всіх вхідних змінних одним вектором і ввести функції приналежності від декількох змінних. У цьому випадку опис умов в правилах буде мати вигляд [6]:

IF (X це Ak),


де X=[X1,…,Xn]T, а Ak – це нечітка множина з багатовимірної функцією приналежності.

Второй элемент архитектуры – компонент, отвечающий заключениям правил [7]. Використовується рішення, запропоноване Такагі та Сугено, яке докладно описувалося в п. 1.3. Вихід системи висновку являє собою функцію вхідних змінних, т.е.

Y=f(k)(X), 


де  f(k)(X)  – це функція, що міститься в k-му правилі, а Y – чисельне значення керуючого впливу. При об'єднанні обох елементів утворюється база правил наступної форми (позначення R(k) відноситься до відповідних правил):

R(k): IF (X це Ak) THEN Y=f(k)(X).
Процесс всіх етапів показано на анімованому малюнку 3.5.

Процес всіх етапів

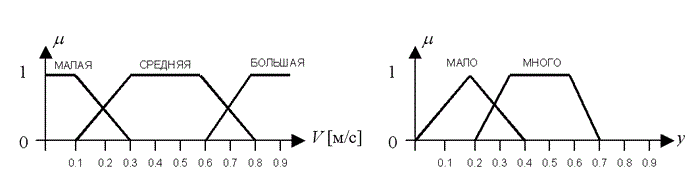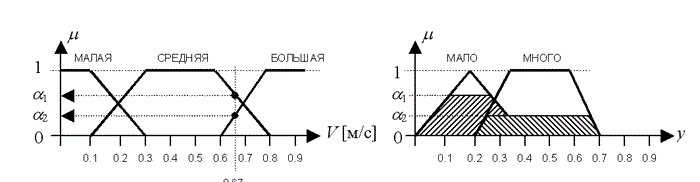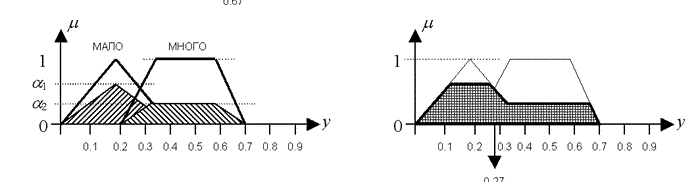
Рисунок 3.5 – Процес всіх етапів

4. Дослідження інформаційних технологій реалізації нечіткого управління

Нечітке моделювання в середовищі MATLAB

Для розробки і подальшого застосування систем нечіткого виводу в інтерактивному режимі можуть бути використані наступні графічні засоби, що входять до складу пакету Fuzzy Logic Toolbox.

1. Редактор систем нечіткого висновку FIS (FIS Еdition) або скорочено peдaктор FIS показано на малюнку 4.1. Редактор систем нечіткого висновку FIS є основним засобом, який використовується для створення або редагування систем нечіткого виводу в графічному режимі. Якщо функція fuzzy викликається без аргументів, то редактор FIS викликається для знову створюваної системи нечіткого висновку з ім'ям Untitled за замовчуванням. При цьому за замовчуванням також задається цілий ряд параметрів, таких як тип системи нечіткого виводу (Мамдані), нечіткі логічні операції, методи імплікації, агрегування і дефаззіфікації і деякі інші.

 

 Графічний інтерфейс редактора FIS

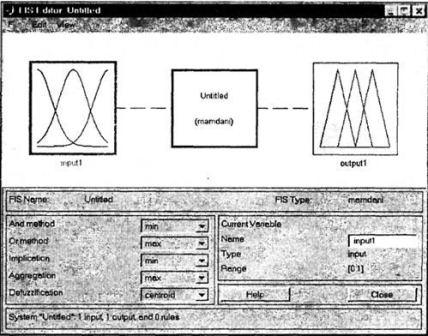
Рисунок 4.1 – Графічний інтерфейс редактора FIS

 

2. Редактор функцій приналежності системи нечіткого виводу (Membership Function Editor) або скорочено редактор функцій належності зображено на малюнку 4.2. Редактор функції приналежності призначено завдання і редагування функцій приладдя окремих термів системи нечіткого виводу в графічному режимі [8].

Для відображення графіків функцій належності слід вибрати необхідну змінну в лівій частині графічного інтерфейсу редактора під заголовком FIS Variables.

 
Редактор функції приналежності, що викликається функцією mfedit

Рисунок 4.2 – Редактор функції приналежності, що викликається функцією mfedit

 

3. Редактор правил системи нечіткого виводу (Rule Еditor) або скорочено редактор правил зображений на малюнку 4.3.

Редактор правил системи нечіткого висновку, як випливає з його назви, призначений для завдання і редагування окремих правил системи нечіткого виводу в графічному режимі.

 Редактор правил, що викликається функцією ruleedit

Рисунок 4.3 – Редактор правил, що викликається функцією ruleedit

 
Редактор правил має головне меню, яке дозволяє користувачеві викликати інші графічні засоби роботи з системою нечіткого висновку FIS, завантажувати і зберігати структуру FIS в зовнішніх файлах і т. д.

4. Програма перегляду правил системи нечіткого виводу (Rule Viewer) або скорочено переглядач правил виводу на малюнку 4.4;

Головне призначення програми перегляду правил полягає у можливості візуалізувати результати нечіткого виводу і отримувати значення вихідних змінних залежно від вихідних значень вхідних змінних [9].

Програма перегляду правил не дозволяє редагувати правила і функції приналежності термів змінних і використовується після розробки системи нечіткого виведення на етапі її аналізу та оцінки. Функцію також доцільно використовувати в тому випадку, коли необхідно візуально представити весь процес нечіткого висновку від початку до кінця. При цьому користувач має віз потужність оцінити значення вихідних змінних нечіткої моделі і вплив кожного з правил на результат нечіткого висновку допомогою зміни значень вхідних змінних;

Програма перегляду правил, викликана функцією ruleview  

Рисунок 4.4 – Програма перегляду правил, викликана функцією ruleview

 

­5. Програма перегляду поверхні системи нечіткого виводу (Surfасе Viewer) або скорочено переглядач поверхні виведення на малюнку 4.5.

Програма перегляду поверхні системи нечіткого висновку дозволяє переглядати поверхню системи нечіткого виводу і візуалізувати графіки залежності вихідних змінних від окремих вхідних змінних.

Програма перегляду поверхні висновку не дозволяє вносити зміни в систему нечіткого виводу і відповідну їй структуру FIS. Використовуючи головне меню програми, користувач може вибрати вхідні змінні і відповідні їм горизонтальні осі системи координат (Х і У), а також вихідну змінну, якій відповідає вертикальна вісь системи координат (Z).

Програма перегляду поверхні виведення, що викликається функцією surfview

 
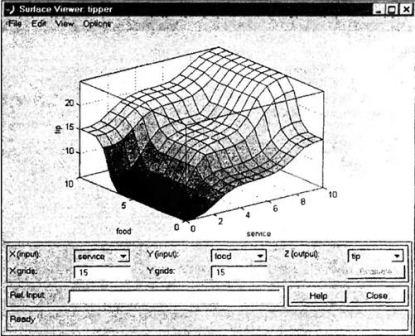
Рисунок 4.5 – Програма перегляду поверхні виведення, що викликається функцією surfview

 

Крім цих графічних засобів до складу пакету Fuzzy Logic Toolbox також входять наступні спеціальні програми [10]:

1. Редактор адаптивних систем нейро-нечіткого виводу (Adaptive Neuro-Fuzzy Inference System Editor) або скорочено редактор гібридних мереж або редактор ANFIS на малюнку 4.6.

Подальше настроювання параметрів побудованої і навченої гібридної мережі може бути виконана за допомогою розглянутих раніше стандартних графічних засобів пакету Fuzzy Logic Toolbox. Для цього рекомендується зберегти створену систему нечіткого виводу в зовнішньому файлі з розширенням fis, після чого слід завантажити цей файл в редактор систем нечіткого висновку FIS.

 Графічний інтерфейс редактора FIS для згенерованої системи нечіткого висновку

Рисунок 4.6 – Графічний інтерфейс редактора FIS для згенерованої системи нечіткого висновку

 

2. Програма нечіткої кластеризації методом нечітких середніх (fuzzy з-means clustering) на малюнку 4.7.

Таким чином, система MATLAB дозволяє вирішувати завдання нечіткої кластеризації двома способами: за допомогою функцій командного рядка і за допомогою графічного інтерфейсу кластеризації. Перший з них є більш трудомістким, але володіє більшою гнучкістю і можливістю відображення у вікні команд значень матриць центрів нечітких кластерів, функцій належності і цільової функції. Другий спосіб видається найбільш зручним для виконання деякої серії розрахунків для різних значень вхідних параметрів з метою візуального аналізу отриманих результатів.

Результат розв'язання задачі нечіткої кластеризації алгоритмом FCM за допомогою графічного інтерфейсу для безлічі даних

Рисунок 4.7 – Результат розв'язання задачі нечіткої кластеризації алгоритмом FCM за допомогою графічного інтерфейсу для безлічі даних

Нечітке моделювання в середовищі fuzzyTECH

Програма fuzzyTECH, розроблена і постійно оновлювана підприємством INFORM GmbH (Inform Software Corporation, Німеччина), призначена для вирішення різних завдань нечіткого моделювання. На відміну від системи МАTLAB, програма fuzzyTECH є спеціалізованим засобом, який дозволяє розробляти і досліджувати різноманітні нечіткі моделі в графічному режимі, а також перетворювати їх в програмний код на одній з мов програмування з можливістю подальшої реалізації в програмованих мікроконтролерах. 

Програма fuzzyTECH володіє можливістю використання її в якості сервера або клієнта при нечіткому управлінні віддаленими об'єктами. Цікавою особливістю програми fuzzyTECH, яку також слід обов'язково зазначити, є можливість автоматичної генерації документації з нечітким моделям у вигляді тексту з ілюстраціями у форматі RTF.

Хоча програма fuzzyTECH і система МАTLAB використовують єдині принципи нечіткого моделювання, існує кілька принципових відмінностей у реалізації систем нечіткого висновку FLS в програмі fuzzyTECH від раніше розглянутих систем FIS в пакеті Fuzzy Logic Toolbox. Головні з них викладені нижче [11].

1. Проект системи нечіткого виводу в fuzzyTECH може мати кілька блоків правил (Rule Blocks) нечітких продукцій, кожен з яких може містити власні вхідні та вихідні лінгвістичні змінні. При цьому окремі блоки правил можуть з'єднуватися між собою послідовним або паралельним чином як зображено намалюнку 4.8.

2. Крім вхідних (Inputs) і вихідних (Outputs) лінгвістичних змінних проекти fuzzyTECH можуть мати так звані проміжні (Intеrmеdiаtеs) лінгвістичні змінні. Ці змінні з'являються в тих випадках, коли блоки правил з'єднуються послідовно, тобто вихід одного блоку правил з'єднується з входом іншого блоку правил як зображено на малюнку 4.8.

 Вікно редактора проекту програми fuzzyTECH

 

Рисунок 4.8 – Вікно редактора проекту програми fuzzyTECH

 

3. Всі операції з розробки, редагуванню, налагодженні та аналізу проектів у програмі fuzzyTECH виконуються в графічному інтерактивному режимі, при цьому для створення прототипів проектів і специфікації їх окремих компонентів можуть бути використані різні майстри (Wizards).

4. На основі розробленого і налагодженого проекту програмою fuzzyTECH може бути згенерований програмний код реалізації системи нечіткого виведення на одній з мов програмування (С, Java, MS Visual С + +, MS Visual Basic, MS VBA, COBOL, Assembler, мова m-файлів системи MATLAB ). У подальшому отримані подібним чином листинги програмного коду можуть бути відкомпільовані для тієї чи іншої обчислювальної платформи та використані незалежно від програми fuzzyTECH для реалізації в нечітких мікроконтролерах.

5.  Використання в програмі fuzzyTECH технології динамічного обміну даними (DDE) дозволяє спільно використовувати розроблені нечіткі моделі з іншими програмами та інструментами, такими як MS Access, MS Excel, MATLAB. При цьому програма fuzzyTECH може виступати як у ролі сервера, так і в ролі клієнта, що істотно розширює діапазон можливих додатків розроблюваних нечітких моделей. В останньому випадки для нечіткого управління віддаленими об'єктами необхідно використовувати той чи інший протокол передачі даних (TCP / IP, IPX / SPX) і додаткові інтерфейси (послідовний інтерфейс RS232, SDI 5, SFS, FTOCC).

6.  Всі проекти в середовищі fuzzyTECH зберігаються в окремих файлах проектів формату FTL (Fuzzy Technology Language), які мають розширення ftl. Вони являють собою звичайні текстові файли, які можна переглядати і редагувати будь-яким АSСII – редактором (наприклад, MS Notebook). Формат FTL був спеціально розроблений компаніями Intel Corp. і Inform Sоftware Corp. в 1991 r. для представлення систем нечеткоrо виведення у формі структурованого тексту. Цей формат підтримують всі провідні розробники програмних і апаратних рішень, заснованих на використанні систем нечіткої логіки, дозволяючи здійснити їх перенесення на різні платформи.

7.  Крім формату FТL, файли проектів можуть бути представлені у форматі FTR (fuzzyTECH Runtime), відповідно, з розширенням ftr. Файли формату FTR, на відміну від формату FTL, представляють проекти в бінарному вигляді. При цьому форма подання залежить від використовуваної версії програми fuzzyTECH. Файл формату FTR містить всю інформацію про проект і може бути використаний для перетворення у відповідний файл проекту формату FTL..

8. У нечітких проектах fuzzyTECH можуть бути використані різні типи і форми функцій належності термів лінгвістичних змінних. Що стосується типів функцій приналежності, то користувач може вибрати один з варіантів, наведених нижче:

– стандартний варіант функції приналежності (Standard MBFs), який іноді називають "4-крапковим" варіантом, оскільки заснований на використанні 4 характеристичних точок або параметрів для завдання відповідної функції приналежності;

– довільний варіант функції приналежності (Arbitrary MBFs), в рамках якого можна використовувати до 16 характеристичних точок або параметрів для завдання або апроксимації відповідної функції приналежності;

– інверсний варіант функції приналежності (Inverse MBFs), який може виявитися корисним при визначенні правил нечітких продукцій з запереченням існуючих в проекті термів (inverse terms) для окремих лінгвістичних змінних;

9.  Кожен з типів функції приналежності може мати одну з форм, при веденні нижче:

– лінійну (L-shape), яка передбачає подання функції приналежності у формі трикутної, трапецієподібної функції або їх деякої комбінації;

– S-подібну (S-shape), яка передбачає подання функції приналежності у формі деякої S-подібної, Z-подібної або П-подібної кривої.й.

10. У програмі fuzzyTECH можуть бути різні методи фазифікації вхідних змінних. При цьому користувач може вибрати один з наступних варіантів фазифікації:

– стандартний метод фазифікації (Compute MBF) передбачає використання функцій належності стандартного типу трикутних, трапецієвидних і кусково-лінійних кривих;;

– нечіткий вхід (Fuzzy Input) вказує, що всі терми відповідної лінгвістичної змінної подаються у формі вектора значень функції приналежності. Цей варіант більш ефективний при реалізації систем нечіткого висновку на конкретній апаратній платформі;

– нечіткий вхід у формі таблиці (Look-up-MBF) вказує, що нечіткі значення відповідної лінгвістичної змінної обчислюються за допомогою деякого алгоритму і представляються у формі таблиці. Цей варіант може бути використаний для збільшення швидкості обчислень на деяких типах мікроконтролерів і нечітких мікропроцесорів;

– швидкий метод фазифікації (Fast Computation of MBF) є різновидом стандартного методу стосовно до деяких конкретних типів мікроконтролерів. Цей варіант має найбільшої ефективністю при використанні конкретної апаратної платформи;

– звичайний вхід (Categorical) вказує, що всі терми відповідної лінгвістичної змінної подаються у формі звичайного вектора значень.

11. У нечітких проектах fuzzyTECH можуть бути також використані різні методи агрегування, композиції, акумуляції та дефаззіфікації отриманих результатів нечіткого виводу;

12. Для композиції висновків правил нечітких продукцій користувач може скористатися одним з таких варіантів завдання вагових коефіцієнтів правил::

– стандартний (Standard), при якому значення вагового коефіцієнта для кожного правила передбачається незмінним і рівним 1;

– визначається користувачем (Fuzzy Associative Maps або скорочено FАМ), при якому значення вагового коефіцієнта DoS для каждоrо правила можна змінювати в межах інтервалу [О, 1].

13. Для акумуляції висновків правил нечітких продукцій користувач може скористатися одним з таких методів:

– звичайним (мах), при якому результат нечіткого виводу в блоці правил нечітких продукцій визначається як об'єднання нечітких множин;

– граничної суми (bsum), при якому результат нечіткого виводу в блоці правил нечітких продукцій визначається як об'єднання нечітких множин.

14. У проектах fuzzyTECH можуть бути використані різні методи дефаззіфікації вихідних змінних. При цьому користувачеві надається можливість вибору одного з таких методів дефаззіфікації:

– стандартний метод (Center-of-Maximum або скорочено СОМ), який, на думку розробників, представляється методом найкращого компромісу для отримання остаточного значення вихідних змінних. У програмі fuzzyTECH метод дефаззіфікації Сом працює аналогічно методу центру ваги СоО;

– метод центру площі (Сеnter-оf-Аrеа або скорочено СоА);

– метод середнього максимуму (Mean-of-Maximum або скорочено МоМ), який, на думку розробників, представляється найбільш гнучким методом і визначається як арифметичне середнє між лівим і правим модальними значеннями, при цьому в якості моди нечіткої множини розглядається максимальне значення її функції приналежності;

– метод Гіперцентр максимуму (Нуреr Center-of-Maximum або скорочено HyperCoM), який може бути використаний тільки в додаткових модулях програми fuzzyTECH. Цей метод дозволяє враховувати позитивні і негативні результати нечітких висновків і відповідно до цього формує деякий оптимальне значення для вихідних змінних.

 Графічне вікно перегляду тривимірної поверхні нечіткого виводу 

Рисунок 4.9 – Графічне вікно перегляду тривимірної поверхні нечіткого виводу

 

    Система МАTLAB. розроблена і постійно оновлювана підприємством MathWorks Inc. (США), є однією з найбільш відомих систем комп'ютерної математики. До останніх прийнято відносити спеціалізовані комп'ютерні програми, які призначені для вирішення широкого класу задач, пов'язаних з тим чи іншим розділом теоретичної чи прикладної математики. При цьому окремі класи завдань, які дозволяє вирішувати система МАTLAB, мають досить умовне відношення до класичної математики, оскільки в даний час представляють собою вузько спеціалізовані галузі наукових і прикладних досліджень. Використання системи MATLAB і пов'язаних з нею методик моделювання і процедур виконання чисельних розрахунків стало стандартом de facto для найширшого кола фахівців із різних галузей науки, техніки, економіки та освіти. Містить спеціальні засоби нечіткого моделювання, система МАTLAB дозволяє виконувати весь комплекс досліджень з розробки та застосування нечітких моделей. Саме з цих причин була обрана система MATLAB для розробки нового методу нечіткого управління на основі функцій приналежності кількох змінних.

Висновки

Основний результат представленої роботи полягає в тому, що були розглянуті алгоритми нечіткого управління, а також варіанти програмних середовищ для реалізації алгоритму в системі. 

Однією з основних причин використання нечіткої логіки для механізму оцінки є можливість завдання необхідної залежності мовою, близькою до природного. Найбільш відповідні бази для цього бази знань застосовуються в методах Мамдані, Ларсен і в новому алгоритмі, що описаний в пункті 2.1. Алгоритм нечіткого висновку забезпечує гнучкість системи прийняття рішення за рахунок коригування критеріїв оцінки і правил виводу.

У даній роботі були досліджені різні середовища розробок. MatLAB має більше можливостей ніж MathCAD, Maple та Mathematica, так як цей пакет настільки універсальний, що може вирішувати майже весь спектр завдань. MathCAD, Maple та Mathematica більше спрямований на вирішення різних рівнянь з чіткими вхідними даними, а також більш простіше в написанні коду. 

Виходячи, з описаних середовищ реалізації алгоритму нечіткого управління був зроблений висновок, що MathLab – це середовище з кращими можливостями реалізації даного алгоритму з відображенням результатів у вигляді багатовимірних графіків, а також з більш зрозумілим графічним інтерфейсом.

Таким чином, реалізація ПП, який забезпечує вирішення завдань з нечіткими вхідними даними, є актуальним завданням. Проведений аналіз і сама постановка завдання показують, що новий алгоритм і ПП буде забезпечувати адекватний та ефективний вивід рішення задач користувачів.

При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: січень 2014 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після вказаної дати.

Перелік посилань

1. Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений. – М.: Мир, 1976. –[djvu]

2.     Заде Л.А. Тени нечетких множеств – [pdf]

3.     Губко М.В. Лекции по принятию решений в условиях нечеткой информации – [pdf]

4.  Круглов В.В., Дли М.И. Интеллектуальные информационные системы: компьютерная поддержка систем нечеткой логики и нечеткого вывода. – М.: Физматлит, 2002.

5.     Леоненков А.В. Нечеткое моделирование в среде MATLAB и fuzzyTECH. – СПб., 2003.

6. Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы. – М., 2004.

7.Масалович А. Нечеткая логика в бизнесе и финансах. www.tora-centre.ru/library/fuzzy/fuzzy–.htm

8.  Kosko B. Fuzzy systems as universal approximators // IEEE Transactions on Computers, vol. 43, No. 11, November 1994. – P. 1329–1333.

9.  Cordon O., Herrera F., A General study on genetic fuzzy systems // Genetic Algorithms in engineering and computer science, 1995. – P. 33–57.

10. Тарасевич, Ю.Ю. Математическое и компьютерное моделирование / Тарасевич, Ю.Ю. – М.: Едиториал УРСС, 2004. – 152 с. 

11. Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы: Пер. с польск. И. Д. Рудинского. –М.: Горячая линия –Телеком, 2006. –452 c