1. Актуальность темы
2. Цель и задачи исследования, планируемые результаты
3. Обзор существующих методов нечеткого управления на основе функций принадлежностей нескольких аргументов
4. Исследование информационных технологий реализации нечеткого управления
Выводы
Список источников
Введение
В области управления
техническими системами
нечеткое
моделирование позволяет получать более адекватные результаты по
сравнению с
результатами, которые основываются на использовании традиционных
аналитических
моделей и алгоритмов управления. Диапазон применения нечетких методов с
каждым
годом расширяется, охватывая такие области, как проектирование
промышленных
роботов и бытовых электроприборов, управление доменными печами и
движением
поездов метро, автоматическое распознавание речи и изображений.
Нечеткая логика, которая служит основой для реализации методов нечеткого управления, более естественно описывает характер человеческого мышления и ход его рассуждений, чем традиционные формально логические системы. Именно поэтому изучение и использование математических средств для представления нечеткой исходной информации позволяет строить модели, которые наиболее адекватно отражают различные аспекты неопределенности, постоянно присутствующей в окружающей нас реальности.
Обработка нечеткой информации и нечеткий вывод давно применяются в различных интеллектуальных системах, однако наиболее широкое распространение нечеткие системы системы получили в области управления.
В
классических нечетких регуляторах не предусмотрены механизмы адаптации
в реальном времени к изменяющимся характеристикам взаимодействия
объекта управления с окружающей средой, что не позволяет применять
нечеткие системы для управления объектами с изменяющимся во времени
свойствами. Однако существует ряд методов, расширяющих возможности
нечетких регуляторов в этой области.
1. Актуальность темы
Обработка нечеткой информации и нечеткий вывод давно применяются в различных интеллектуальных системах, однако наиболее широкое распространение нечеткие системы получили в области управления. Для управления плохо формализуемыми объектами со сложной взаимосвязью управляющих переменных предложено использовать метод на основе функций принадлежности термов нескольких аргументов. Для практического использования метода актуально создание специализированного программного обеспечения.
2. Цель и задачи исследования, планируемые результаты
Целью исследования является разработка и анализ алгоритмов нечеткого управления на основе функций принадлежности нескольких переменных.
Основные задачи исследования:
- Обзор существующих методов нечеткого управления на основе функций принадлежности одного аргумента.
- Обзор существующих методов нечеткого управления на основе функций принадлежности нескольких аргументов.
- Исследование информационных технологий реализации нечеткого управления.
3. Обзор существующих методов нечеткого управления на основе функций принадлежностей нескольких аргументов
Адаптация метода Мамдани к использованию функций принадлежности нескольких переменных
Методика построения
нечеткого регулятора на
основе
термов с функциями принадлежности нескольких аргументов представлена на
рисунке 3.1. Построение нечеткого регулятора включает в себя следующую
последовательность действий:
- Постановка задачи нечеткого управления;
- Формирование термов и их функций принадлежности;
- Формирование базы правил системы нечеткого вывода;
- Фаззификация входных переменных;
- Агрегирование подусловий в нечетких правилах продукций;
- Активизация подзаключений в нечетких правилах продукций;
- Аккумулирование заключений нечетких правил продукций;
- Дефаззификация выходных переменных.
В рамках постановки задачи
определяются
входные и
выходные переменные объекта управления, на основе входных переменных
выбираются
управляющие переменные. Выделенные величины представляются в виде
лингвистических
переменных.
Для каждой из
лингвистических переменных
формируются
терм-множества в виде нечетких переменных [1].
Если лингвистическая
переменная
обладает простой структурой, то для нее могут быть выбраны термы в виде
нечетких переменных с одномерной функцией принадлежности. Иначе
рекомендуется
использовать нечеткие переменные с многомерными функциями
принадлежности. К
формированию названий термов и их функций принадлежности могут быть
привлечены
эксперты. Кроме этого, для определения числа термов и вида их функций
принадлежности могут быть использованы методы нечеткого кластерного
анализа. В
дальнейшем для построения многомерных функций принадлежности в работе
используется метод нечетких с-средних.

Рисунок
3.1 –
Методика построения
нечеткого регулятора
на основе многомерных функций принадлежности
База правил системы нечеткого вывода формируется на основе эмпирических знаний или знаний экспертов в проблемной области и представляется в виде нечетких продукций [2]: P = {R1, R2, ...,Rp} – ммножество правил нечетких продукций; B = {B1, B2, ...,Bm} – множество входных лингвистических переменных; W = {W1, W2, ...,Wz} – множество выходных лингвистических переменных.
Правило Rr: Если ПУlkir то ПУzbjr
ПЗjr : B1 ЕСТЬ Btlk,
Sir – степень истинности подусловия ПУlkir.
ПЗjr : Wz ЕСТЬ Wtzb,
где Wtzb – b-тый терм выходной лингвистической переменной Wz,
Zir – степень истинности подзаключения ПУlkir
Процедура фазификации
заключается в
установлении
соответствия между конкретным значением отдельной входной переменной
системы
нечеткого вывода и значением Sir функции
принадлежности соответствующего ей
терма входной лингвистической переменной, которая, в случае многомерных
функций,
рассчитывается по формуле многомерной табличной интерполяции
(полиномами Эрмита) [3]:
где ẍl –
значение входной переменной системы нечеткого вывода;
µlk
(ẍl) –
функция
принадлежности к-го
терма, входящего
в подусловие ПУlkir.
Агрегирование представляет
собой процедуру
определения
степени истинности условий по каждому из правил системы нечеткого
вывода.
Если
условие правила задано в
форме
нечетких лингвистических высказываний вида «β
есть α»,
этап их агрегирования
оставляет степени истинности без изменения. Если же условие состоит из
нескольких подусловий, причем лингвистические переменные в подусловиях
попарно
не равны друг другу, то определяется степень истинности сложного
высказывания
на основе известных значений истинности подусловий. При этом для
определения
результата используется формула:
На этапе агрегирования
находятся все значения
Sr для
каждого из правил,
входящих в
рассматриваемую базу правил системы нечеткого вывода.
На этапе активизации для
каждой из выходных
лингвистических переменных, входящих в отдельные подзаключения правил
нечетких
продукций, определяются функции принадлежности нечетких множеств их
значений [4].
Расчет значения функции принадлежности каждого из подзаключений для рассматриваемых выходных лингвистических переменных осуществляется по формуле:
где µlk (ÿz) – функция принадлежности b-того терма;
Zir
–
степень истинности каждого из подзаключений, рассчитываемая
по формуле:
где Kr –
весовой
коэффициент правила.
Этап аккумуляции заключается в том, чтобы объединить или аккумулировать с использованием операции max–дизъюнкции все степени истинности заключений для получения функции принадлежности каждой из выходных переменных:
Дефаззификации заключается в том, чтобы, используя результаты аккумуляции всех выходных лингвистических переменных, получить обычное количественное значение каждой из выходных переменных, которое может быть использовано специальными устройствами, внешними по отношению к системе нечеткого вывода. Для одномерных функций принадлежности применяется стандартный метод центра тяжести. Для многомерного случая используется обобщение метод центра тяжести:
где yzn*
–
результат
дефаззификации;
Vz – объем фигуры,
образованной функцией
принадлежности µlk
*(ÿz).
Нечеткий вывод, основанный на нейронной сети
Очень часто делается
допущение, что входные
переменные
независимы друг от друга [5].
Это обусловливает разделение на классы,
иллюстрируемое на рисунке 3.2.

Рисунок
3.2 –
Классическое разделение
входного
пространства на области
Белое поле означает
принадлежность к данному
классу,
серое поле – частичную принадлежность к каждому из
соседствующих
классов (либо
отсутствие принадлежности к классу).
При таком подходе каждая входная переменная имеет собственные входные множества. Они содержатся в условиях правил в виде:
R1 :
IF (X1
это ОТРИЦАТЕЛЬНОЕ AND X2 это БОЛЬШОЕ),
R2 :
IF (X1
это ОТРИЦАТЕЛЬНОЕ AND X2 это МАЛОЕ),
R1 : IF (X1
< X2),
R2 : IF (X1 ≈
X2),
для
которой классический подход оказывается не самым целесообразным.

Рисунок
3.3 –
Предлагаемое разделение
входного
пространства на классы
В качестве решения можно предложить замену всех входных переменных одним вектором и ввести функции принадлежности от нескольких переменных. В этом случае описание условий в правилах будет иметь вид [6]:
где X=[X1,…,Xn]T, а Ak –
это нечеткое множество с многомерной функцией принадлежности.
Второй элемент архитектуры – компонент, отвечающий заключениям правил [7]. Используется решение, предложенное Такаги и Сугено, которое подробно описывалось в п. 1.3. Выход системы вывода представляет собой функцию входных переменных, т.е
где f(k)(X) – это функция, содержащаяся в k-м правиле, а Y – численное значение управляющего воздействия. При объединении обоих элементов образуется база правил следующей формы (обозначение R(k) относится к соответствующим правилам):
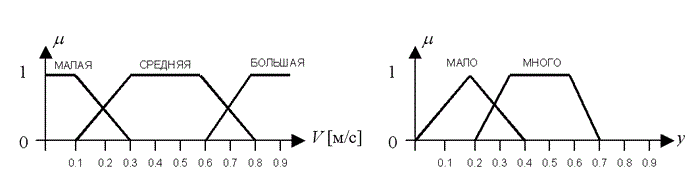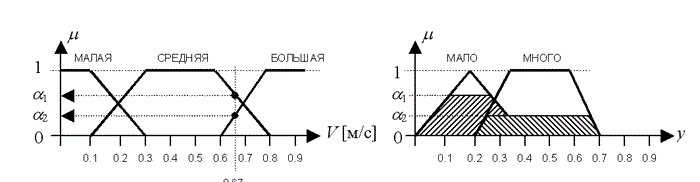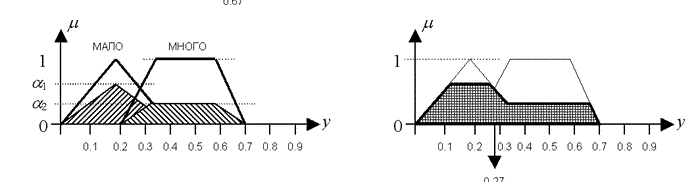
Рисунок 3.5 – Процесс всех этапов
4 Исследование информационных технологий реализации нечеткого управления
Нечеткое моделирование в среде MATLAB
Для разработки и дальнейшего
применения
систем
нечеткого вывода в интерактивном режиме могут быть
использованы
следующие
графические средства, входящие в состав пакета Fuzzy Logic Toolbox.
1. Редактор
систем нечеткого вывода FIS (FIS Еdition) или
сокращенно peдaктор FIS показано на рисунке 4.1.
Редактор
систем нечеткого
вывода FIS является основным средством, которое используется для
создания или
редактирования систем нечеткого вывода в графическом режиме. Если
функция fuzzy
вызывается без аргументов, то редактор FIS вызывается для вновь
создаваемой
системы нечеткого вывода с именем Untitled по умолчанию. При этом по
умолчанию
также задается целый ряд параметров, таких как тип системы нечеткого
вывода
(Мамдани), нечеткие логические операции, методы импликации,
агрегирования и дефаззификации
и некоторые другие.
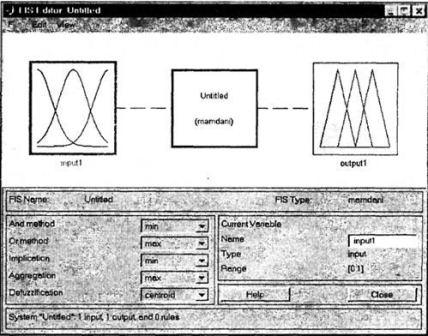
Рисунок
4.1 –
Графический интерфейс
редактора FIS
2. Редактор функций
принадлежности системы
нечеткого
вывода (Membership Function Editor) или сокращенно редактор
функций
принадлежности изображено на рисунке 4.2. Редактор функции
принадлежности
предназначен для задания и редактирования функций принадлежностей
отдельных
термов системы нечеткого вывода в графическом режиме [8].
Для отображения графиков
функций
принадлежности
следует выбрать необходимую переменную в левой части графического
интерфейса
редактора под заголовком FIS Variables.

Рисунок
4.2 –
Редактор функции
принадлежности,
вызываемый функцией mfedit
3. Редактор правил системы
нечеткого вывода
(Rule
Еditor) или сокращенно редактор правил изображенный на рисунке
4.3.
Редактор правил системы
нечеткого вывода, как
следует
из его названия, предназначен для задания и редактирования
отдельных правил
системы нечеткого вывода в графическом режиме.

Рисунок
4.3 –
Редактор правил,
вызываемый функцией
ruleedit
Редактор правил имеет
главное меню, которое
позволяет
пользователю вызывать другие графические средства работы с
системой нечеткого
вывода FIS, загружать и сохранять структуру FIS во внешних файлах и т.
д.
4. Программа просмотра
правил системы
нечеткого вывода
(Rule Viewer) или сокращенно просмотрщик правил вывода на
рисунке
4.4;
Главное назначение программы
просмотра правил
заключается в возможности визуализировать результаты нечеткого вывода и
получать значения выходных переменных в зависимости от исходных
значений
входных переменных [9].
Программа просмотра правил
не позволяет
редактировать
правила и функции принадлежности термов переменных и используется после
разработки системы нечеткого вывода на этапе ее анализа и оценки.
Функцию также
целесообразно использовать в том случае, когда необходимо визуально
представить
весь процесс нечеткого вывода от начала до конца. При этом
пользователь имеет
воз мощность оценить значения выходных переменных нечеткой
модели
и влияние
каждого из правил на результат нечеткого вывода посредством изменения
значений
входных переменных;

Рисунок
4.4 –
Программа просмотра
правил, вызванная
функцией ruleview
5. Программа
просмотра поверхности
системы нечеткого
вывода (Surfасе Viewer) или сокращенно просмотрщик
поверхности
вывода на
рисунке 4.5.
Программа просмотра
поверхности системы
нечеткого
вывода позволяет просматривать поверхность системы нечеткого вывода и
визуализировать графики зависимости выходных переменных от отдельных
входных
переменных.
Программа просмотра
поверхности вывода не
позволяет
вносить изменения в систему нечеткого вывода и соответствующую ей
структуру
FIS. Используя главное меню программы, пользователь может выбрать
входные
переменные и соответствующие им горизонтальные оси системы координат
(Х и У), а также выходную
переменную, которой
соответствует вертикальная ось системы координат (Z).
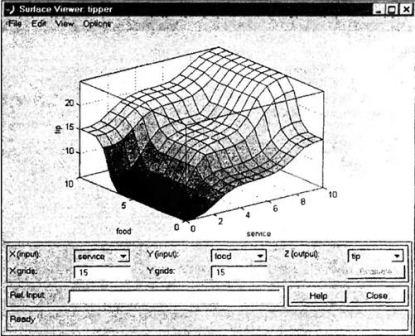
Рисунок 4.5 – Программа просмотра
поверхности вывода,
вызываемая функцией surfview
Кроме этих графических
средств в состав
пакета Fuzzy
Logic Toolbox также входят следующие специальные программы [10]:
1. Редактор адаптивных
систем нейро-нечеткого
вывода
(Adaptive Neuro-Fuzzy Inference System Editor) или сокращенно
редактор
гибридных сетей или редактор ANFIS на рисунке 4.6.
Дальнейшая настройка
параметров построенной и
обученной гибридной сети может быть выполнена с помощью рассмотренных
ранее
стандартных графических средств пакета Fuzzy Logic Toolbox.
Для
этого
рекомендуется сохранить созданную систему нечеткого вывода во внешнем
файле с
расширением fis, после чего следует загрузить этот файл в
редактор
систем
нечеткого вывода FIS.

Рисунок
4.6 –
Графический интерфейс
редактора FIS для
сгенерированной системы нечеткого вывода
2. Программа нечеткой
кластеризации методом
нечетких
средних (fuzzy с-means clustering) на рисунке 4.7.
Таким образом, система
MATLAB позволяет
решать задачи нечеткой
кластеризации двумя способами: с помощью функций командной
строки
и с помощью
графического интерфейса кластеризации. Первый из них является более
трудоемким,
но обладает большей гибкостью и возможностью отображения в окне команд
значений
матриц центров нечетких кластеров, функций принадлежности и целевой
функции.
Второй способ представляется наиболее удобным для выполнения
некоторой серии
расчетов для различных значений входных параметров с целью
визуального анализа
полученных результатов.

Нечеткое моделирование в среде fuzzyTECH
Программа fuzzyTECH,
разработанная и
постоянно
обновляемая компанией INFORM GmbH (Inform Software Corporation,
Германия),
предназначена для решения различных задач нечеткого моделирования. В
отличие от
системы МАTLAB, программа fuzzyTECH является специализированным
средством,
которое позволяет разрабатывать и исследовать разнообразные нечеткие
модели в
графическом режиме, а также преобразовывать их в программный код на
одном из
языков программирования с возможностью последующей реализации в
программируемых
микроконтроллерах.
Программа fuzzyTECH обладает
возможностью
использования ее в качестве сервера или клиента при нечетком управлении
удаленными объектами. Интересной особенностью программы
fuzzyTECH,
которую
также следует обязательно отметить, является возможность автоматической
генерации документации по нечетким моделям в виде текста с
иллюстрациями в
формате RTF.
Хотя программа fuzzyTECH и
система МАTLAB
используют
единые принципы нечеткого моделирования, существует несколько
принципиальных
отличий в реализации систем нечеткого вывода FLS в программе fuzzyTECH
от ранее
рассмотренных систем FIS в пакете Fuzzy Logic Toolbox. Главные из них
изложены
ниже [11].
1. Проект системы нечеткого
вывода в
fuzzyTECH может
иметь несколько блоков правил (Rule Blocks) нечетких продукций, каждый
из
которых может содержать собственные входные и выходные лингвистические
переменные. При этом отдельные блоки правил могут соединяться между
собой
последовательным или паралельным образом как изображено нарисунке 4.8.
2. Кроме входных (Inputs) и выходных (Outputs) лингвистических переменных проекты fuzzyTECH могут иметь так называемые промежуточные (Intеrmеdiаtеs) лингвистические переменные. Эти переменные появляются в тех случаях, когда блоки правил соединяются последовательно, т. е. выход одного блока правил соединяется с входом другого блока правил как изображено на рисунке 4.8.

3. Все операции по
разработке,
редактированию, отладке
и анализу проектов в программе fuzzyTECH выполняются в графическом
интерактивном режиме, при этом для создания прототипов проектов и
спецификации
их отдельных компонентов могут быть использованы различные мастера
(Wizards).
4. На основе разработанного
и отлаженного
проекта
программой fuzzyTECH может быть сгенерирован программный код реализации
системы
нечеткого вывода на одном из языков программирования (С, Java, MS
Visual С++,
MS Visual Basic, MS VBA, COBOL, Assembler, язык m-файлов
системы
MATLAB). В
дальнейшем полученные подобным образом листинги программного кода могут
быть
откомпилированы для той или иной вычислительной платформы и
использованы
независимо от программы fuzzyTECH для реализации в нечетких
микроконтроллерах.
5. Использование в программе
fuzzyTECH
технологии
динамического обмена данными (DDE) позволяет совместно использовать
разработанные нечеткие модели с другими программами и инструментами,
такими как
MS Access, MS Excel, MATLAB. При этом программа fuzzyTECH может
выступать как в
роли сервера, так и в роли клиента, что существенно расширяет диапазон
возможных приложений разрабатываемых нечетких моделей. В последнем
случаи для
нечеткого управления удаленными объектами необходимо использовать тот
или иной
протокол передачи данных (TCP/IP, IPX/SPX) и дополнительные интерфейсы
(последовательный интерфейс RS232, SDI 5, SFS, FTOCC).
6. Все проекты в среде
fuzzyTECH сохраняются
в
отдельных файлах проектов формата FTL (Fuzzy Technology Language),
которые
имеют расширение ftl. Они представляют собой обычные текстовые файлы,
которые
можно просматривать и редактировать любым АSСII-редактором
(например, MS
Notebook). Формат FTL был специально разработан компаниями Intel Corp.
и Inform
Sоftware Corp. в 1991 r. для представления систем нечеткоrо вывода в
форме
структурируемого текста. Этот формат поддерживают все ведущие
разработчики
программных и аппаратных решений, основанных на использовании
систем нечеткой
логики, позволяя осуществить их перенос на различные платформы.
7. Кроме формата FТL, файлы
проектов могут
быть
представлены в формате FTR (fuzzyTECH Runtime), соответственно, с
расширением
ftr. Файлы формата FTR, в отличие от формата FTL, представляют проекты
в
бинарном виде. При этом форма представления зависит от
используемой версии
программы fuzzyTECH. Файл формата FTR содержит всю информацию о проекте
и может
быть использован для преобразования в соответствующий файл
проекта
формата
FTL.
8. В нечетких проектах
fuzzyTECH могут быть
использованы различные типы и формы функций принадлежности термов
лингвистических переменных. Что касается типов функций принадлежности,
то
пользователь может выбрать один из вариантов, приведенных ниже:
– стандартный
вариант функции
принадлежности (Standard
MBFs), который иногда называют "4-точечным" вариантом,
поскольку
основан на использовании 4 характеристических точек или параметров для
задания
соответствующей функции принадлежности;
– произвольный
вариант функции
принадлежности
(Arbitrary MBFs), в рамках которого можно использовать до 16
характеристических
точек или параметров для задания или аппроксимации соответствующей
функции
принадлежности;
– инверсный
вариант функции
принадлежности (Inverse
MBFs), который может оказаться полезным при определении правил нечетких
продукций с отрицанием существующих в проекте термов (inverse terms)
для
отдельных лингвистических переменных;
9. Каждый из типов функции
принадлежности
может иметь
одну из форм, при веденных ниже:
– линейную
(L-shape), которая
предполагает
представление функции принадлежности в форме треугольной,
трапециевидной
функции или их некоторой комбинации;
–
S-образную (S-shape),
которая предполагает
представление функции принадлежности в форме некоторой
S-образной, Z-образной
или П-образной кривой.
10. В программе fuzzyTECH
могут быть
различные методы
фаззификации входных переменных. При этом пользователь может выбрать
один из
следующих вариантов фаззификации:
– стандартный
метод фаззификации
(Compute MBF)
предполагает использование функций принадлежности стандартного
типа
треугольных, трапециевидных и кусочно-линейных кривых;
– нечеткий
вход (Fuzzy Input)
указывает, что все
термы соответствующей лингвистической переменной представляются в форме
вектора
значений функции принадлежности. Этот вариант более эффективен при
реализации
систем нечеткого вывода на конкретной аппаратной платформе;
– нечеткий вход в
форме таблицы
(Look-up-MBF)
указывает, что нечеткие значения соответствующей лингвистической
переменной
вычисляются с помощью некоторого алгоритма и представляются в форме
таблицы.
Этот вариант может быть использован для увеличения скорости вычислений
на
некоторых типах микроконтроллеров и нечетких микропроцессоров;
– быстрый метод
фаззификации (Fast
Computation of MBF)
является разновидностью стандартного метода применительно к
некоторым
конкретным типам микроконтроллеров. Этот вариант обладает наибольшей
эффективностью
при использовании конкретной аппаратной платформы.
– обычный
вход (Categorical)
указывает, что все
термы соответствующей лингвистической переменной представляются в форме
обычного вектора значений.
11. В нечетких проектах
fuzzyTECH могут быть
также
использованы различные методы агрегирования, композиции, аккумуляции и
дефаззификации полученных результатов нечеткого вывода;
12. Для композиции
заключений правил
нечетких
продукций пользователь может воспользоваться одним из следующих
вариантов
задания весовых коэффициентов правил:
– стандартный
(Standard), при
котором значение
весового коэффициента для каждого правила предполагается неизменным и
равным 1;
– определяемый
пользователем
(Fuzzy Associative
Maps или сокращенно FАМ), при котором значение весового
коэффициента DoS для
каждоrо правила можно изменять в пределах интервала [О, 1].
13. Для аккумуляции
заключений правил
нечетких
продукций пользователь может воспользоваться одним из следующих
методов:
– обычным (mах),
при котором результат
нечеткого
вывода в блоке правил нечетких продукций определяется как объединение
нечетких
множеств;
– граничной суммы
(bsum), при котором
результат
нечеткого вывода в блоке правил нечетких продукций определяется как
объединение
нечетких множеств.
14. В проектах fuzzyTECH
могут быть
использованы
различные методы дефаззификации выходных переменных. При этом
пользователю
предоставляется возможность выбора одного из следующих методов
дефаззификации:
– стандартный
метод
(Center-of-Maximum или сокращенно
СоМ), который, по мнению разработчиков, представляется
методом
наилучшего
компромисса для получения окончательного значения выходных переменных.
В
программе fuzzyTECH метод дефаззификации СоМ работает аналогично методу
центра
тяжести СоО;
– метод центра
площади (Сеnter-оf-Аrеа или
сокращенно СоА);
– метод
среднего максимума
(Mean-of-Maximum или
сокращенно МоМ), который, по мнению разработчиков, представляется
наиболее
гибким методом и определяется как арифметическое среднее между левым и
правым
модальными значениями, при этом в качестве моды нечеткого множества
рассматривается максимальное значение ее функции принадлежности;
– метод
гиперцентра максимума (Нуреr
Center-of-Maximum
или сокращенно HyperCoM), который может быть
использован
только в
дополнительных модулях программы fuzzyTECH. Этот метод позволяет
учитывать
положительные и отрицательные результаты нечетких выводов и в
соответствии с
этим формирует некоторое оптимальное значение для выходных
переменных.

Рисунок 4.9 –
Графическое окно
просмотра трехмерной
поверхности нечеткого вывода
Выводы
Основной результат
представленной работы
состоит в
том, что были рассмотрены алгоритмы нечеткого управления, а также
варианты
программных сред для реализации алгоритма в системе.
Одной из основных причин
использования
нечеткой логики для механизма
оценки является возможность задания требуемой зависимости на языке,
близком к естественному.
Наиболее подходящие базы для этого базы знаний применяются в методах
Мамдани,
Ларсен и в новом алгоритме, что описан в пункте 2.1. Алгоритм нечеткого
вывода
обеспечивает гибкость системы принятия решения за счет корректировки
критериев
оценки и правил вывода.
В данной работе были
исследованы различные
среды разработок. MatLAB имеет
больше возможностей нежели MathCAD, Maple и Mathematica, так
как этот пакет настолько универсален, что может
решать почти весь спектр задач.
MathCAD, Maple
и Mathematica больше
направлен на решение различных уравнений с четкими входными данными, а
также более
проще в написании кода.
Исходя, из описанных сред
реализации
алгоритма нечеткого управления был
сделан вывод, что MathLab – это среда с
лучшими
возможностями реализации данного алгоритма с отображением результатов в
виде многомерных графиков, а также с более
понятным графическим интерфейсом.
Таким образом, реализация
ПП, который
обеспечивает решения задач с
нечеткими входными данными, является актуальной задачей.
Список источников
1.
Заде
Л. Понятие
лингвистической
переменной и его применение к принятию приближенных решений.
– М.: Мир,
1976. –[djvu]
2. Заде
Л.А. Тени
нечетких множеств –
[pdf]
3. Губко
М.В. Лекции
по
принятию решений
в
условиях нечеткой информации –
[pdf]
4. Круглов
В.В., Дли М.И. Интеллектуальные
информационные
системы: компьютерная поддержка систем нечеткой логики и нечеткого
вывода. –
М.: Физматлит, 2002.
5. Леоненков
А.В. Нечеткое
моделирование в среде MATLAB и
fuzzyTECH. – СПб., 2003.
6. Рутковская
Д., Пилиньский М., Рутковский Л. Нейронные
сети, генетические алгоритмы и нечеткие системы.
– М., 2004.
7.Масалович
А. Нечеткая логика в бизнесе и финансах. www.tora-centre.ru/library/fuzzy/fuzzy–.htm
8. Kosko
B. Fuzzy systems as universal approximators //
IEEE Transactions on
Computers, vol. 43, No.
11,
November 1994. – P. 1329–1333.
9. Cordon
O., Herrera F., A General study on genetic
fuzzy systems // Genetic
Algorithms in
engineering and
computer science, 1995. – P. 33–57.
10. Тарасевич, Ю.Ю. Математическое и компьютерное моделирование / Тарасевич, Ю.Ю. – М.: Едиториал УРСС, 2004. – 152 с.
11. Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы: Пер. с польск. И. Д. Рудинского. –М.: Горячая линия –Телеком, 2006. –452 c.


