Портал магістрів ДонНТУ

Супонін Олег Олегович

Я

Факультет комп'ютерних наук та технологій

Кафедра комп'ютерної iнженерії

Системне програмування

Група СП-12м

Розробка моделей паралельної системи
прогнозування поведінки рухомого об'єкту

Науковий керівник: д.т.н., проф. Святний В.А

Консультант: Крiвошеев С.В.

Deutch
Deutch
 Deutch
Резюме Біографія
Реферат

Зміст

Вступ

На сьогоднішній день актуальною є тема прогнозування поведінки рухомих об'єктів. Технічний прогрес зробив великий крок вперед і сьогодні створюється величезна безліч проектів, таких як космічні кораблі, морські судна, авіалайнери, поїзди, ракети, автомобілі та інші рухомі об'єкти, які необхідно відслідковувати в просторі і виконувати різноманітні операції контролю і управління. У зв'язку з цим для всіх подібних об'єктів необхідно розраховувати і прогнозувати траєкторію і характеристику руху.

1 Актуальність теми

Прогнозування поведінки рухомого об'єкту у даний час є актуальним питанням, яке полягає в тому, що необхідно заздалегідь знати можливі шляхи поведінки об'єкта в залежності від зовнішніх факторів і заданих критеріїв. Необхідно вирішувати проблеми тимчасового обмеження, пов'язані з розрахунком і визначенням місця розташування об'єкта.

2 Алгоритм генерації траєкторії

Розрахунок траеторіі здійснюється за допомогою алгоритмів Флойда-Уоршелла, Дейкстри, які будуть представлені далі.

2.1 Алгоритм Флойда-Уоршелла

Даний алгоритм призначений для знаходження найкоротших відстаней між усіма вершинами зваженого орієнтованого графа. Розроблено в 1962 році Робертом Флойдом і Стівеном Уоршелла. Більш сувора формулювання цього завдання наступна: [4]
є орієнтований граф G = (V, Е) кожній дузі v -> w цього графа зіставлено вартість C [v, w]. Загальна задача знаходження найкоротших шляхів полягає в знаходженні для кожної впорядкованої пари вершин v, w) будь-якого шляху від вершини v в вершини w, довжина якого мінімальна серед усіх можливих шляхів від v до w.

Формальний опис
   Є послідовно пронумеровані від 1 до n вершини графа. Алгоритм Флойда використовує матрицю А розміру п * n, в якій обчислюються довжини найкоротших шляхів. Спочатку A [i, j] = C [i, j] для всіх i! = J. Якщо дуга i - »j відсутній, то C [i, j] = infinity. Кожен діагональний елемент матриці А дорівнює 0.

Над матрицею А виконується п ітерацій. Після k-й ітерації A [i, j] містить значення найменшої довжини шляхів з вершини i у вершину у, які не проходять через вершини з номером, більшим k. Іншими словами, між кінцевими вершинами шляху i і у можуть знаходитися тільки вершини, номери яких менше або дорівнюють k. На k-й ітерації для обчислення матриці А застосовується наступна формула:
A k [i, j] = min (A k-1 [i, j], A k-1 [i, k] + A k-1 [k, j])
Нижній індекс k позначає значення матриці А після k-й ітерації, але це не означає, що існує п різних матриць, цей індекс використовується для скорочення запису. Для обчислення A k [i, j] проводиться порівняння величини A ki [i, j] (тобто вартість шляху від вершини i до вершини j без участі вершини k або іншої вершини з більш високим номером) з величиною A k-1 [i, k] + A k-1 [k, j] (вартість шляху від вершини i до вершини k плюс вартість шляху від вершини k до вершини j). Якщо шлях через вершину k дешевше, ніж A k-1 [i, j], то величина A k [i, j] змінюється.

Оцінка складності
Час виконання цієї програми має порядок 0 (V 3 ), оскільки в ній тільки три вкладених один в одного циклу. Доказ "правильності" роботи цього алгоритму також очевидно і виконується за допомогою математичної індукції по k, показуючи, що на k-й ітерації вершина k включається в дорогу тільки тоді, коли новий шлях коротший старого.

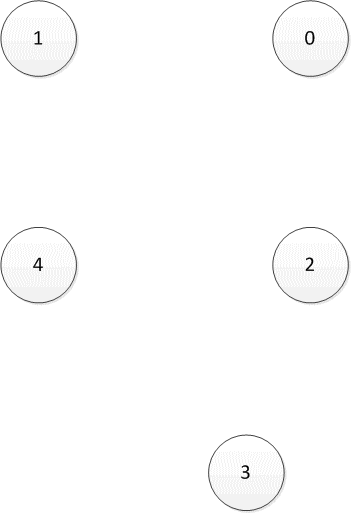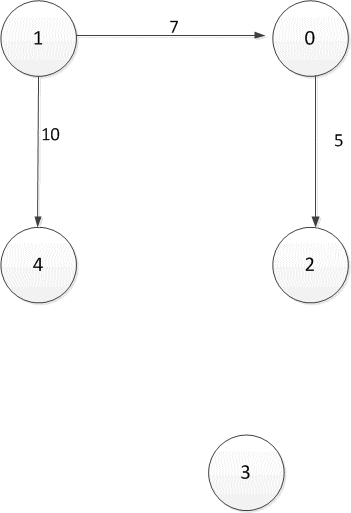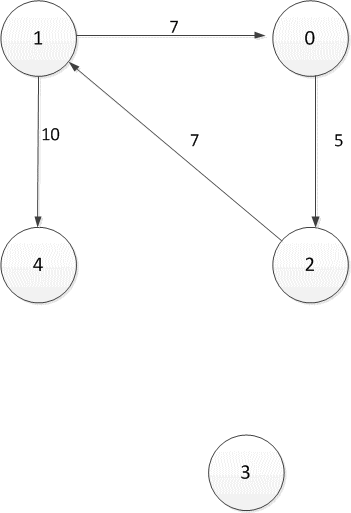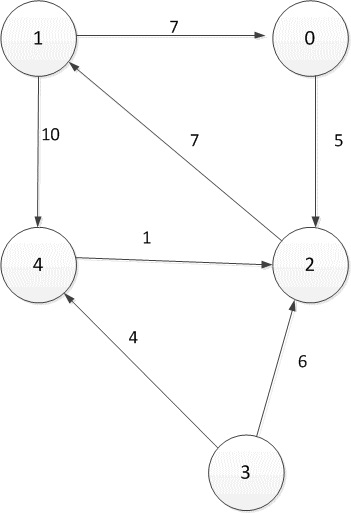
Орієнтований спрямований граф
Рисунок 2.1 — Орієнтований спрямований граф
(6 фреймів, 10 сек тривалість, 11 kb)

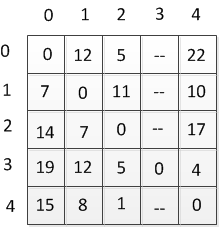
Таблиця 2.1 — Таблиця відстаней

2.2 Алгоритм Дейкcтри
Адгорітм знаходить найкоротша відстань від однієї з вершин графа до всіх інших. Алгоритм працює тільки для графів без ребер негативного ваги і широко застосовується в програмуванні і технологіях.
Суть алгоритму буде розглянута далі. [3]
Мається орієнтований граф G, який зображений на рисунку 2.2


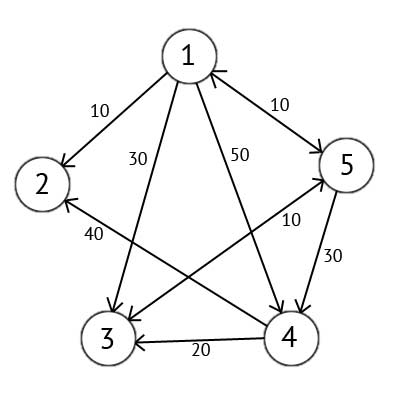
Рисунок 2.2 — Орієнтований граф G

Цей граф ми можемо представити у вигляді матриці С:

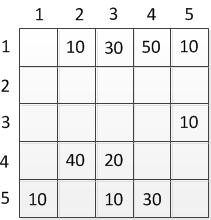
Таблиця 2.2 — Матриця орієнтованого графа

Виберемо вершину 1. Це означає, що будемо шукати найкоротші маршрути з вершини 1 у вершини 2, 3, 4 і 5. Даний алгоритм покроково перебирає всі вершини графа і призначає їм мітки, які є відомим мінімальним відстанню від вершини джерела до конкретної вершини. Розглянемо цей алгоритм на прикладі. Привласнимо 1-й вершині мітку що дорівнює 0, тому як ця вершина - джерело. Решті вершин присвоїмо мітки рівні нескінченності.


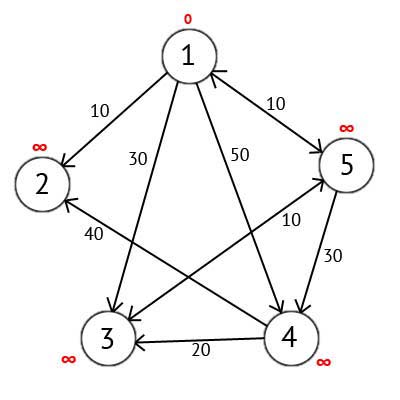
Рисунок 2.3 — Орієнтований граф після першого кроку

Далі виберемо таку вершину W, яка має мінімальну позначку і розглянемо всі вершини в які з вершини W є шлях, який не містить вершин посередників. Кожній з розглянутих вершин призначимо мітку рівну сумі мітки W і довжини шляху з W у розглянуту вершину, але тільки в тому випадку, якщо отримана сума буде менше попереднього значення мітки. Якщо ж сума не буде менше, то залишаємо попередню мітку без змін.


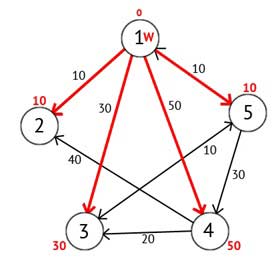
Рисунок 2.4 — Орієнтований граф після другого кроку

Далі вершину W відзначаємо як відвідану, і вибираємо із ще не відвіданих таку, яка має мінімальне значення мітки, вона і буде наступною вершиною W. У даному випадку це вершина 2 або 5. Якщо є кілька вершин з однаковими мітками, то не має значення яку з них можна вибрати як W.

Виберемо вершину 2. З неї немає ні одного вихідного шляху, значить можна відразу відзначити вершину як відвідану і перейти до наступної вершини з мінімальною міткою. На цей раз тільки вершина 5 має мінімальну позначку. Розглянемо всі вершини в які є прямі шляхи з 5, але які ще не помічені як відвідані. Знову знаходимо суму мітки вершини W і ваги ребра з W в поточну вершину, і якщо ця сума буде менше попередньої мітки, то замінюємо значення мітки на отриману суму.


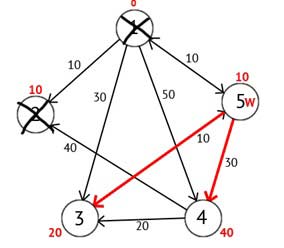
Рисунок 2.5 — Орієнтований граф після третього кроку

Виходячи з картинки можна побачити, що мітки 3-ей і 4-ої вершин стали менше, тобто був знайдений більш короткий маршрут в ці вершини з вершини джерела. Далі відзначаємо 5-у вершину як відвідану і вибираємо наступну вершину, яка має мінімальну позначку. Повторюємо всі перераховані вище дії до тих пір, поки їсти не відвідані вершини.
Виконавши всі дії, отримаємо такий результат:


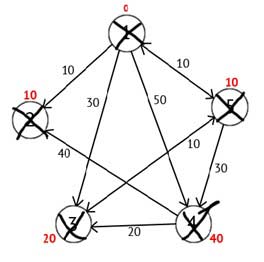
Рисунок 2.6 — Орієнтований граф на кінцевому кроці

3 Фільтр Калмана

Фільтрація — це алгоритм обробки даних, який прибирає шуми і зайву інформацію. Для поліпшення якості сигналу необхідно проводити фільтрацію. Одним з поширених фільтрів є фільтр Калмана.

Фільтр Калмана — це алгоритм фільтрації, використовуваний в багатьох областях науки і техніки. Його можна зустріти в GPS-приймачах, обробниках інтелектуальних датчиків, в різних системах управління.

Вимірювальні прилади володіють деякою погрішністю. Це може призвести до того, що інформація з нього виявляється зашумленной. Чим сильніше зашумлені дані тим складніше обробляти таку інформацію.

Фільтр Калмана використовує динамічну модель системи. Алгоритм складається з двох повторюваних фаз: передбачення і коригування. На першому розраховується пророкування стану в наступний момент часу (з урахуванням неточності їх виміру). На другому, нова інформація з датчика коригує передбачене значення (також з урахуванням неточності і зашумленности цієї інформації):


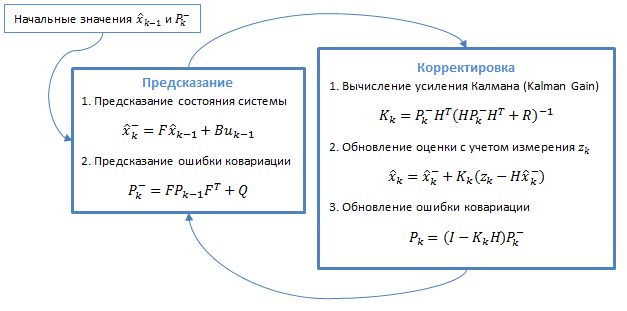
Рисунок 3.1 - Загальний алгоритм фільтра

3.1 Модель динамічної системи

Фільтри Калмана базуються на дискретизованої за часом лінійних динамічних системах. Стан системи описується вектором кінцевої розмірності — вектором стану. У кожен такт часу лінійний оператор діє на вектор стану і переводить його в інший вектор стану (детерміноване зміна стану), додається деякий вектор нормального шуму (випадкові фактори) і в загальному випадку вектор управління, що моделює вплив системи управління.

При використанні фільтра Калмана для отримання оцінок вектора стану процесу по серії зашумлених вимірювань необхідно представити модель даного процесу у відповідності зі структурою фільтра - у вигляді матричного рівняння певного типу. Для кожного такту k роботи фільтру необхідно відповідно з наведеним нижче описом визначити матриці: переходу між процесами F k ; матрицю вимірів H k ; ковариационную матрицю шуму процесу Q k ; ковариационную матрицю шуму вимірювань R k ; за наявності керуючих впливів - матрицю їх коефіцієнтів B k .



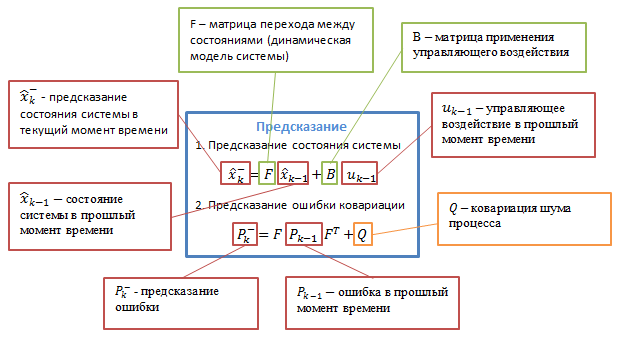
Рисунок 3.2 — Детальний опис алгоритму [9]
x k = F k x k-1 + B k u k + w k , де F k — матриця еволюції процесу /системи, яка впливає на вектор x k-1 (вектор стану в момент k-1 );
B k — матриця управління, яка прикладається до вектора керуючих впливів u k ;
w k — нормальний випадковий процес з нульовим математичним очікуванням і ковариационной матрицею Q k , який описує випадковий характер еволюції системи /процесу: w k ~ N (0, Q ).
У момент k здійснюється спостереження (вимірювання) z k істинного вектора стану x k , які пов'язані між собою рівнянням: z k = H k x k + v k , де
H k — матриця вимірювань, що зв'язує істинний вектор стану і вектор проведених вимірювань, v k — білий гауссовский шум вимірювань з нульовим математичним очікуванням і ковариационной матрицею R k : v k ~ N (0, R k )

Фільтр Калмана є різновидом рекурсивних фільтрів. Для обчислення оцінки стану системи на поточний такт роботи йому необхідна оцінка стану (у вигляді оцінки стану системи та оцінки похибки визначення цього стану) на попередньому такті роботи та вимірювання на поточному такті. Дана властивість відрізняє його від пакетних фільтрів, що вимагають в поточний такт роботи знання історії вимірювань та /або оцінок. Далі під записом X n | m будемо розуміти оцінку істинного вектора x в момент n з урахуванням вимірювань з моменту початку роботи і за момент m включно.

P k | k — апостериорная коваріаційна матриця помилок, що задає оцінку точності отриманої оцінки вектора стану і включає в себе оцінку дисперсій похибки обчисленого стану і коваріації, що показують виявлені взаємозв'язку між параметрами стану системи (у російськомовній літературі часто позначається D k );
X k | k — апостериорная оцінка стану об'єкта в момент k отримана за результатами спостережень аж до моменту k включно (в російськомовній літературі часто позначається X k , де X ́ означає "оцінка", а k — номер такту, на якому вона отримана).

В якості рухомого об'єкту виберемо судно, рух якого описується системою диференціальних рівнянь. [8]


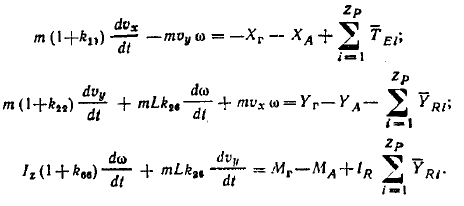
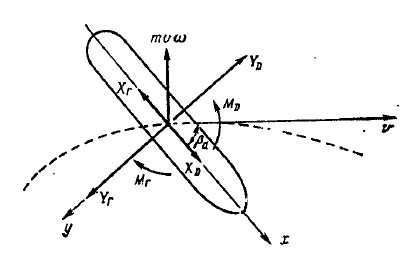
Рисунок 3.3 — модель судна в циркуляційному басейні.

4 Паралельні архітектури

В даний час для підвищення швидкодії обчислювальних систем широко застосовуються різні підходи. Одним з них є використання багатоядерних і багатопроцесорних обчислювальних архітектур. [1]

4.1 Паралелізм як основа високопродуктивних обчислень

Багатопроцесорні системи можна класифікувати таким чином:
SISD (Single Instruction Single Data) — одиночний потік команд, одиночний потік даних (послідовні комп'ютери фон Неймана). До цього класу належать послідовні комп'ютернi системи, які мають одне центральний процесор, здатний обробляти тільки один потік послідовно виконуваних інструкцій. Це звичайні скалярні, однопроцесорні системи. [10]

SIMD ((Single Instruction Multiple Data) — характеризуються наявністю одиночного потоку команд, але множинного потоку даних. До цього класу належать однопроцесорні, векторно-конвеєрні суперкомп'ютери.

Іншим підкласом SIMD-систем є векторні комп'ютери. Векторні комп'ютери маніпулюють масивами схожих даних подібно до того, як скалярні машини обробляють окремі елементи таких масивів. Це робиться за рахунок використання спеціально сконструйованих векторних центральних процесорів. [10]

MIMD — архітектура комп'ютера, яка використовується для досягнення високопродуктивних паралельних обчислень. Особливість даної системи полягає в тому, що обчислювач має декілька процесорів, які функціонують асинхронно і незалежно. Різні процесори в будь-який момент можуть виконувати різні команди над різними частинами даних. MIMD архітектури далі класифікуються в залежності від фізичної організації пам'яті, тобто чи має процесор свою власну локальну пам'ять і звертається до інших блоків пам'яті, використовуючи комутуючу мережа, або комутуюча мережа під'єднує всі процесори до загальнодоступної пам'яті. Виходячи з організації пам'яті, розрізняють такі типи паралельнихархітектур: Комп'ютери з розподіленою пам'яттю (Distributed memory) Процесор може звертатися до локальної пам'яті, може посилати і отримувати повідомлення, що передаються по мережі, що з'єднує процесори. Повідомлення використовуються для здійснення зв'язку між процесорами або, що еквівалентно, для читання і запису віддалених блоків пам'яті. У ідеалізованої мережі вартість посилки повідомлення між двома вузлами мережі не залежить як від розташування обох вузлів, так і від трафіку мережі, але залежить від довжини повідомлення. [2]


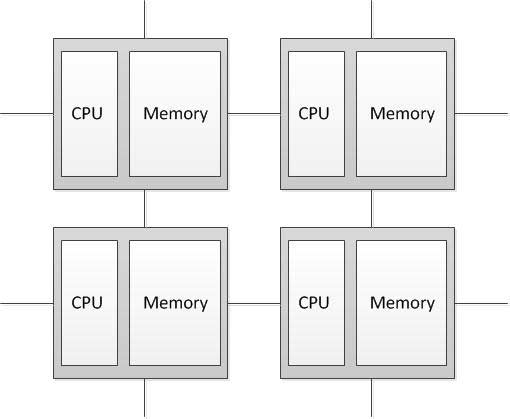
Рисунок 4.1 — Структура комп'ютера з розподіленою пам'яттю

4.2 Паралельні архітектури GPU

Іншим різновидом паралельної архітектури є графічний процесор (англ. graphics processing unit, GPU), яке являє собою окремий пристрій персонального комп'ютера, що виконує графічний рендеринг. Завдяки спеціалізованої конвеєрної архітектурі вони набагато ефективніше в обробці графічної інформації, ніж типовий центральний процесор.

Для прискорення універсальних додатків використовують спільну роботу GPU і CPU для виконання обчислень. Обчислення на GPU були винайдені компанією NVIDIA і швидко стали стандартом в індустрії, яку використовують мільйони користувачів по всьому світу і яку прийняли практично всі виробники комп'ютерних систем.

CPU + GPU — система, яка збільшує обчислювальну потужність за рахунок того, що CPU складаються з декількох ядер, оптимізованих для послідовної обробки даних, в той час як GPU складаються з тисячі ядер, створених для паралельної обробки даних. Послідовні частини коду обробляються на CPU, а паралельні частини — на GPU.


Рисунок 4.2 — CPU + GPU [6]

5 Підходи та реалізації

Паралельні архітектури мають свої особливості у реалізації обчислень. Паралельне програмування застосовується для створення програм, ефективно використовують обчислювальні ресурси за рахунок одночасного виконання коду на декількох обчислювальних вузлах. Для створення паралельних програм використовуються паралельні мови програмування і спеціалізовані системи підтримки паралельного програмування, такі як MPI і CUDA. Паралельне програмування є більш складним у порівнянні з послідовним як у написанні коду, так і в його налагодження.

5.1 MPI

MPI — програмний інтерфейс для передачі інформації, який дозволяє обмінюватися повідомленнями між процесами, які виконують одну задачу. MPI є найбільш поширеним стандартом інтерфейсу обміну даними в паралельному програмуванні, існують його реалізації для великого числа комп'ютерних платформ. Використовується при розробці програм для кластерів і супер комп'ютерів. Основним засобом комунікації між процесами в MPI є передача повідомлень один одному. У першу чергу MPI орієнтований на системи з розподіленою пам'яттю, тобто коли витрати на передачу даних великі. Базовим механізмом зв'язку між MPI процесами є передача і прийом повідомлень. Повідомлення несе в собі передані дані і інформацію, що дозволяє приймаючій стороні здійснювати їх вибірковий прийом: [7]
1. відправник - ранг (номер у групі) відправника повідомлення;
2. одержувач - ранг одержувача;
3. ознака - може використовуватися для розділення різних видів повідомлень;
4. комунікатор - код групи процесів.

Операції прийому і передачі можуть бути блокується і не Блокує. Для не блокують операцій визначено функції перевірки готовності і очікування виконання операції.

5.2 CUDA

CUDA — програмно-апаратна архітектура паралельних обчислень, яка дозволяє істотно збільшити обчислювальну продуктивність завдяки використанню графічних процесорів фірми NVIDIA. [5]
В архітектурі CUDA використовується модель пам'яті типу Grid, кластерне моделювання потоків і SIMD-інструкції. Учені і дослідники широко використовують CUDA в різних областях, включаючи астрофізику, обчислювальну біологію та хімію, моделювання динаміки рідин, електромагнітних взаємодій, комп'ютерну томографію, сейсмічний аналіз і багато іншого. У CUDA є можливість підключення до додатків, що використовують OpenGL і Direct3D. CUDA - крос платформенне програмне забезпечення для таких операційних систем як Linux, Mac OS X і Windows. [6]

6 Висновки

Актуальність використання супер комп'ютерів, а відповідно і паралельної архітектури, при прогнозуванні поведінки рухомого об'єкту полягає в необхідності проводити розрахунки параметрів руху об'єкта, його траєкторії шляху і поведінки в залежності від зовнішніх факторів за мінімально можливий час.

При прогнозуванні моделі поведінки рухомого об'єкту вкрай важлива швидкість обчислення, у зв'язку з цим необхідно підвищувати ефективність цих обчислень. Це є основною і актуальним завданням.




Список джерел

1. Parallel Computer Architecture: A Hardware/Software Approach (The Morgan Kaufmann Series in Computer Architecture and Design), Callifornia, 1999, 1025c
2. MIMD – архитектура.Електроний ресурс. Режим доступу:
http://www.ccas.ru/paral/mimd/mimd.html
3. Алгоритм Дейкстри. Електроний ресурс. Режим доступу:
http://habrahabr.ru/post/111361/
4. Алгоритм Флойда-Уоршелла. Електроний ресурс. Режим доступу:
http://urban-sanjoo.narod.ru/floyd.html
5. CUDA. Електроний ресурс. Режим доступу:
http://www.nvidia.ru/object/what_is_cuda_new_ru.html
6. CUDA Parallel Computing Platform. Електроний ресурс. Режим доступу: http://www.nvidia.com/object/cuda_home_new.html
7. Message Passing Interface Forum. Електроний ресурс. Режим доступу:
http://www.mpi-forum.org/
8. Ходкость и управляемость судов. Под ред. В.Г. Павленко. М.: Транспорт, 1991., с. 318.
9. Фiльтр Калмана. Електроний ресурс. Режим доступу:
http://habrahabr.ru/post/140274/
10. SIMD та SISD. Електроний ресурс. Режим доступу:
http://rudocs.exdat.com/docs/index-43961.html?page=13
Резюме Біографія
Реферат
© 2013 Oleg Suponin, All rights reserved.