Реферат по теме выпускной работы
Содержание
- Введение
- 1. Актуальность темы
- 2. Цель и задачи исследования
- 3. Обзор исследований и разработок
- 3.1 Обзор международных источников
- 3.2 Обзор национальных источников
- 4. Нечетко–множественный метод оценки риска банкротства
- Выводы
- Список источников
Введение
Любая сфера экономической деятельности сопровождается явлением риска. Страхование относится к тем видам деятельности, которые сильно подвержены этому явлению. Фактор риска и необходимость покрытия возможного ущерба в результате его проявления вызывают потребность в страховании.
Точное измерение риска осуществляется различными количественными методами: математическими, статистическими, методами теории вероятности, теорией игр и многими другими. Риск в страховании сопровожден большой мерой неопределенности, отсутствием выраженной закономерности и его невозможно задать четкими числовыми данными. Эти факторы ограничивают использование классических методов статистического анализа и возникает необходимость разработки новых методов оценки, к которым можно отнести системы с нечеткой логикой.
1. Актуальность темы
Актуальность темы исследования определяется необходимостью своевременного выявления неблагоприятных тенденций в деятельности страховой компании посредством методов нечеткой логики.
Простота нечеткой логики как методологии разрешения проблем гарантирует ее успешное использование во встроенных системах контроля и анализа информации. В отличие от традиционной математики, требующей на каждом шаге моделирования точных и однозначных формулировок закономерностей, нечеткая логика предлагает совершенно иной уровень мышления, благодаря которому творческий процесс моделирования происходит на наивысшем уровне абстракции, при котором постулируется лишь минимальный набор закономерностей.
2. Цель и задачи исследования
Цель работы – сформировать комплексный подход к оценке риска банкротства страховой компании.
Объект исследования – риск банкротства страховой компании.
Предмет исследования – изучение взаимосвязи между качественными переменными и величиной риска банкротства.
Основные задачи исследования:
- Рассмотреть теоретические аспекты анализа риска;
- Выявить взаимосвязь между показателями функционирования страховой компании и риском банкротства;
- Измерить риск банкротства в количественном выражении
3. Обзор исследований и разработок
Аппарат теории нечетких множеств, продемонстрировав ряд многообещающих возможностей применения – от систем управления летательными аппаратами до прогнозирования итогов выборов, оказался вместе с тем сложным для воплощения. Учитывая имеющийся уровень технологии, нечеткая логика заняла свое место среди других специальных научных дисциплин – где-то посредине между экспертными системами и нейронными сетями.
3.1 Обзор международных источников
Нечёткая логика (англ. fuzzy logic) и теория нечётких множеств – раздел математики, являющийся обобщением классической логики и теории множеств. Понятие нечёткой логики было впервые введено профессором Лотфи Заде в 1965 году. В его статье понятие множества было расширено допущением, что функция принадлежности элемента к множеству может принимать любые значения в интервале [0...1], а не только 0 или 1. Такие множества были названы нечёткими. Также автором были предложены различные логические операции над нечёткими множествами и предложено понятие лингвистической переменной, в качестве значений которой выступают нечёткие множества [7].
Большой вклад в развитие методов нечеткой логики в сфере прикладных систем внесли японские ученые, такие как Т. Тэрано, К. Асаи. Именами ученых М. Сугэно и М. Мамдани названы методы логического вывода [6].
Среди российских специалистов можно выделить А.О.Недосекина, который в своей диссертации «Методологические основы моделирования финансовой деятельности с использованием нечетко-множественных описаний» применил аппарат нечеткой логике в области финансового менеджмента [1].
3.2 Обзор национальных источников
Среди отечественных ученых большой популярностью пользуются труды С.Д. Штовбы. В его работе «Проектирование нечетких систем средствами MATLAB» рассмотрены такие вопросы, как проектирование нечетких систем в основополагающем пакете Fuzzy Logic Toolbox в среде MATLAB. Также даны нужные сведения в области теории нечеткой логики и нечетких множеств [3].
Не менее известны труды А.П. Ротштейна. В книге «Интеллектуальные технологии идентификации» предложен метод двухэтапной идентификации нелинейных зависимостей с помощью нечетких баз знаний [10].
4. Нечетко-множественный метод оценки риска банкротства
Исследование состояния теории нечетких множеств применительно к экономике и финансам показывает, что уже созданы все необходимые формализмы для моделирования финансовых систем, однако нынешний уровень модельных представлений отстает от запросов практики финансового менеджмента. Нечеткие множества практически не применялись до настоящего времени для финансового анализа и планирования корпораций, оценки инвестиционной привлекательности ценных бумаг, для оптимизации фондового портфеля и прогнозирования [5].
Рассматривая роль нечетко-множественных описаний для финансового моделирования, в работе отмечается, что такие модели и методы на их основе являются законными правоприемниками вероятностных моделей и методов, с одной стороны, и экспертных методов, с другой стороны.

Рисунок
1 – Взаимосвязь классических
вероятностных, экспертных и нечетко-множественных описаний
(анимация 4 кадра, 6 циклов повторений, 101
килобайт)
Модель Альтмана построена с использованием экспертного аппарата мультипликативного дискриминантного анализа (МДА), который позволяет подобрать такие показатели, дисперсия которых между группами была бы максимальной, а внутри группы минимальной. В результате МДА построена модель Альтмана (Z-счет), имеющая следующий вид [5]:

где K1 = собственный оборотный капитал/сумма активов;
K2= перераспределенная прибыль/сумма активов;
K3= прибыль до уплаты процентов/сумма активов;
K4= рыночная стоимость собственного капитала/стоимость заемного капитала;
K5= объем продаж/сумма активов;
В результате подсчета Z – показателя для конкретного предприятия делается заключение:
если Z < 1,81 – очень высокая вероятность банкротства;
если 1,81 < Z <2,7 – высокая вероятность банкротства;
если 2,7 < Z < 2,99 – возможно банкротство;
если Z > 30 – вероятность банкротства крайне мала.
В экономике Украины модель Альтмана пока не получила широкого применения по следующим причинам [2]:
- Требуется вычисление соответствующих коэффициентов при показателях Ki, i=1..5, которые, отличаются от их значений для зарубежных стран;
- Информация о финансовом состоянии анализируемых предприятий, как правило, недостоверна, руководство ряда предприятий «сознательно» подправляет свои показатели в финансовых отчетах, что делает невозможным найти достоверные оценки коэффициентов в Z- модели.
Поэтому задача оценки вероятности риска банкротства должна решаться в условиях неопределенности, неполноты исходной информации, и для ее решения предлагается использовать адекватный аппарат принятия решений – нечеткие множества и нечеткие нейронные сети (ННС). Рассмотрим матричный метод прогнозирования банкротства корпораций предложенный доктором экономических наук О.А. Недосекиным [1].
- Эксперт строит лингвистическую переменную со своим терм-множеством значений. Например, «Уровень менеджмента» может иметь следующее терм-множество значений: «Очень низкий, Низкий, Средний, Высокий, Очень высокий» [1].
- Для того, чтобы конструктивно описать лингвистическую переменную, эксперт выбирает соответствующий количественный признак – например, сконструированный специальным образом показатель уровня менеджмента, который принимает значения от нуля до единицы [1].
- Далее эксперт каждому значению лингвистической переменной которая по построению является нечетким подмножеством значений интервала [0,1], ставит в соответствие функцию принадлежности того или иного нечткого множества. Как правило, это трапецеидальная функция принадлежности. Верхнее основание трапеции соответствует полной уверенности эксперта в правильности классификации, а нижнее – уверенности в том, что никакие иные значения интервала [0,1] не попадают в выбранное нечеткое множество [1]. (см. рис.2.)
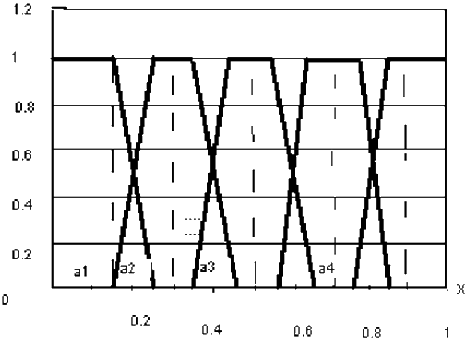
Рисунок 2 – Трапецевидная функция принадлежности
На этом описание лингвистических переменных заканчивается. Нечетко-множественный метод, известный также, как матричный метод, состоит из следующих этапов:
Этап 1 (Лингвистические переменные и нечеткие множества) Лингвистическая переменная Е «Состояние предприятия» имеет пять значений:
E1 – нечеткое подмножество состояний «предельного неблагополучия»;
E2 – нечеткое подмножество состояний «неблагополучия»;
E3 – нечеткое подмножество состояний «среднего уровня»;
E4 – нечеткое подмножество состояний «относительного благополучия»;
E5 – нечеткое подмножество состояний «предельное благополучие».
Соответствующая переменной E лингвистическая переменная G «Риск банкротства» также имеет 5 значений:
G1 – нечеткое подмножество состояний «предельный риск банкротства»;
G2 – нечеткое подмножество состояний «степень риска банкротства высокая»;
G3 – нечеткое подмножество состояний «степень риска банкротства средняя»;
G4 – нечеткое подмножество состояний « низкая степень риска банкротства»;
G5 – нечеткое подмножество состояний «риск банкротства незначительный».
Носитель множества G – показатель степени риска банкротства g – принимает значения от нуля до единицы по определению.
Для отдельного финансового показателя или показателя управления Хi задаем лингвистическую переменную Вi «уровень показателя Хi» на следующем терм-множестве значений:
Bi1 – подмножество «очень низкий уровень показателя Хi»;
Bi2 – подмножество «низкий уровень показателя Хi»;
Bi3 – подмножество «средний уровень показателя Хi»;
Bi4 – подмножество «высокий уровень показателя Хi»;
Bi5 –подмножество «очень высокий уровень показателя Хi».
Этап 2 (Показатели). Построим набор отдельных показателей X={Хi} общим числом N, которые по мнению эксперта, с одной стороны влияют на оценку риска банкротства предприятия, а с другой стороны, оценивают разные по природе стороны деловой и финансовой жизни предприятия. Например, в матричном методе используются такие показатели [8]:
Х1 – коэффициент автономии (отношение собственного капитала к валюте баланса);
Х2 – коэффициент обеспечения оборотных активов собственными средствами (отношение чистого оборотного капитала к оборотным активам);
Х3 – коэффициент промежуточной ликвидности (отношение суммы денежных средств и дебиторской задолженности к краткосрочным пассивам);
Х4 – коэффициент абсолютной ликвидности (отношение суммы денежных средств к краткосрочным пассивам);
Х5 – оборотность всех активов за год(отношение выручки от реализации услуг к средней выручке за период стоимости активов);
Х6 – рентабельность всего капитала (отношение чистой прибыли к средней за период стоимости активов).
Этап 3 (Значимость показателей). Поставим в соответствие каждому показателю Хi уровень его значимости ri. Для того, чтобы оценить этот уровень, необходимо поставить все показатели по порядку уменьшения их значимости так, чтобы выполнялось соотношение [2]:
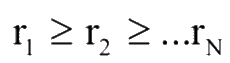
Если система показателей проранжированна в порядке уменьшения их значимости, то вес i-го показателя ri необходимо определять по правилу Фишберна:

Этап 4 (Классификация степени риска). Построим классификацию текущего значения g показателя степени риска как критерий разбиения этого множества на нечеткие подмножества (таблица 1) [1]:
Таблица 1. Классификация степени риска
| Интервал значений g | Классификация уровня параметра | Сложность оценочной уверенности (функция принадлежности) |
| 0<g<0.15 | G5 | 1 |
| 0.15<g<0.25 | G5 | m5 = 10*(0.25 – g) |
| G4 | 1 – m5 = m4 | |
| 0.25<g<0.35 | G4 | 1 |
| 0.35<g<0.45 | G4 | m4 = 10*(0.45 – g) |
| G3 | 1 – m4 = m3 | |
| 0.45<g<0.55 | G3 | 1 |
| 0.55<g<0.65 | G3 | m3 = 10*(0.65 – g) |
| G2 | 1 – m3 = m2 | |
| 0.65<g<0.75 | G2 | 1 |
| 0.75<g<0.85 | G2 | m2 = 10*(0.85 – g) |
| G1 | 1 – m2 = m1 | |
| 0.85<g<1 | G1 | 1 |
Этап 5 (Классификация значений показателей). Построим классификацию текущих значений показателей Х как критерий разбиения полного множества их значений на нечеткие подмножества вида В. Один из примеров такой классификации приведен ниже. В клетках таблицы стоят трапецеидальные нечеткие числа, которые характеризуют соответствующие функции принадлежности.
Этап 6 (Оценка уровня показателей). Проведем оценку текущего уровня показателей и сведем полученные результаты в таблицу 2:
Таблица 2. Текущие значения показателей
| Показатель | Текущее значение |
| X1 | x1 |
| .... | .... |
| Xi | xi |
| .... | .... |
| XN | xN |
Этап 7 (Классификация уровня показателей). Проведем классификацию текущих значений х по критерию таблицы, построенной на этапе 5. Результатом проведенной классификации есть таблица значений уровней принадлежности носителя хi нечетким подмножествам Вj.
Этап 8 (Оценка степени риска). Выполним вычислительные операции для оценки степени риска банкротства [2].

Далее уровень полученного комплексного показателя проходит распознавание по простому правилу или на основе системы трапециевидных функций принадлежности. В частности, простое правило:
g:[0, 0.2] – очень низкий уровень финансового состояния;
g:[0.21, 0.4] – низкий уровень финансового состояния;
g:[0.41, 0.6] – средний уровень финансового состояния;
g:[0.61, 0.8] – высокий уровень финансового состояния;
g:[0.81, 1] – очень высокий уровень финансового состояния.
Построенный метод комплексного анализа финансового состояния корпорации может быть с успехом применен в бизнес-процессе ежеквартального мониторинга состояния корпорации по данным ее финансовой отчетности.
Выводы
Организованные в виде отдельных, целостных структур информационного обеспечения знания о предметной области становятся явными и отделяются от других типов знаний, например общих знаний. Базы знаний позволяют делать выводы опираюсь не только на методы формальной (математической) логики, но и на основе опыта, фактов, эвристик, т.е. они наиболее приближены к человеческой логике. Разработки в области искусственного интеллекта имеют целью использование больших объемов высококачественных специальных знаний о некоторой узкой предметной области для решения сложных, неординарных задач.
База знаний является основой экспертной системы, она накапливается в процессе ее построения. Знание выражаются в явном виде, что позволяет сделать явным способ мышления и решения задач, и организованы так, чтобы упростить принятие решений. База знаний, обусловливает компетентность экспертной системы, воплощает в себе знания специалистов учреждения, отдела, опыт группы специалистов и является институциональным знанием.
При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: январь 2014 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Список источников
- Недосекин А.О. Методологические основы моделирования финансовой деятельности с использованием нечетко-множественных описаний. /Диссертация на соискание ученой степени доктора экономических наук. – Спб.: Санкт-Петербургский государственный университет экономики и финансов, 2003. – 280 с.
- Лузин В.П. Информационно-технические основы создания системы управления крупными рисками в страховой компании. – М.: БУКВИЦА, 2009 – 146 с.
- Штовба С.Д. Проектирование нечетких систем средствами Matlab.– М.: Горячая линия, 2007.
- Гутко Л.М. Страховий ринок Украхни: Стан, проблеми розвитку та шляхи їх вирішення//Менеджент: Оцінка страхового ризику №4,-2009 рік.
- Экономико-математические методы и прикладные модели: Учебное пособие для вузов/В.В. Федосеев, А.Н. Гармаш, И.В. Орлова и др. – М.: ЮНИТИ-ДАНА, 2005.
- Тэрано, Т., Асаи, К., Сугэно, М. Прикладные нёчеткие системы. М.: Мир, 1993. 368c.
- Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений. М.: Мир, 1976. 166c.
- Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы. – М., 2004.
- Круглов В.В., Дли М.И. Интеллектуальные информационные системы: компьютерная поддержка систем нечеткой логики и нечеткого вывода. – М.: Физматлит, 2002.
- Ротштейн А. П. Интеллектуальные технологии идентификации: нечёткая логика, генетические алгоритмы, нейронные сети /А. П. Ротштейн. – Винница: УНИВЕРСУМ-Винница, 1999. – 320 с.
