Реферат за темою випускної роботи
Зміст
- Вступ
- 1. Актуальність теми
- 2. Мета і задачі дослідження та заплановані результати
- 3. Огляд досліджень та розробок
- 3.1 Огляд міжнародних джерел
- 3.2 Огляд національних джерел
- 4. Нечітко–множинний метод аналізу ризику банкрутства
- Висновки
- Перелік посилань
Вступ
Будь яка сфера економічної діяльності супроводжується явищем ризику. Страхування відноситься до тих видів діяльності, які схильні до цього явища. Фактор ризику та необхідність покриття можливого збитку в результаті його прояви викликають потребу в страхуванні.
Точне вимірювання ризику здійснюється різними кількісними методами: математичними, статистичними, методами теорії ймовірності, теорією ігор та іншими. Ризик у страхуванні супроводжений великою мірою невизначеності, відсутністю вираженої закономірності і його неможливо задати чіткими числовими даними. Ці фактори обмежують використання класичних методів статистичного аналізу і виникає необхідність розробки нових методів оцінки, до яких можна віднести системи з нечіткою логікою.
1. Актуальність теми
Aктуальність теми дослідження визначається необхідністю своєчасного виявлення несприятливих тенденцій у діяльності страхової компанії за допомогою методів нечіткої логіки.
Простота нечіткої логіки як методології вирішення проблем гарантує її успішне використання у вбудованих системах контролю та аналізу інформації. На відміну від традиційної математики, що вимагає на кожному кроці моделювання точних і однозначних формулювань закономірностей, нечітка логіка пропонує зовсім інший рівень мислення, завдяки якому творчий процес моделювання відбувається на найвищому рівні абстракції, при якому постулюється лише мінімальний набір закономірностей.
2. Мета і задачі дослідження
Мета роботи – сформувати комплексний підхід до оцінки ризику банкрутства страхової компанії.
Об'єкт дослідження – ризик банкрутства страхової компанії.
Предмет дослідження – вивчення взаємозв'язку між якісними змінними і величиною ризику банкрутства.
Завдання дослідження:
- Розглянути теоретичні аспекти аналізу ризику банкрутства;
- Дослідити залежність між показниками функціонування страхової компанїї та можливим ризиком банкрутства;
- Вимірити ризик банкрутства у вигляді певної величини;
3. Огляд досліджень та розробок
3.1 Огляд міжнародних джерел
Нечітка логіка (англ. fuzzy logic) і теорія нечітких множин – розділ математики, що є узагальненням класичної логіки і теорії множин. Поняття нечіткої логіки було вперше введено професором Лотфі Заде в 1965. У його статті поняття безлічі було розширено допущенням, що функція приналежності елемента до безлічі може приймати будь-які значення в інтервалі [0...1], а не тільки 0 або 1. Такі безлічі були названі нечіткими. Також автором були запропоновані різні логічні операції над нечіткими множинами і запропоновано поняття лінгвістичної змінної, в якості значень якої виступають нечіткі множини [7].
Великий внесок у розвиток методів нечіткої логіки в сфері прикладних систем внесли японські вчені, такі як Т.Терано, К.Асаі. Іменами вчених М.Сугено і М.Мамдані названі методи логічного висновку [6].
Серед російських фахівців можна виділити А.О.Недосекіна, який у своїй дисертації "Методологічні основи моделювання фінансової діяльності з використанням нечітко-множинних описів" застосував апарат нечіткої логіки в галузі фінансового менеджменту [1].
3.2 Огляд національних джерел
Серед вітчизняних вчених великою популярністю користуються праці С.Д. Штовба. У його роботі "Проектування нечітких систем засобами MATLAB" розглянуті такі питання, як проектування нечітких систем в основоположному пакеті Fuzzy Logic Toolbox в середовищі MATLAB. Також дані потрібні відомості в області теорії нечіткої логіки та нечітких множин [3].
Не менш відомі праці А.П. Ротштейна. У книзі "Інтелектуальні технології ідентифікації" запропонований метод двохетапної ідентифікації нелінійних залежностей за допомогою нечітких баз знань [10].
4. Нечітко-множинний метод аналізу ризику банкрутства
Дослідження стану теорії нечітких множин стосовно до економіки та фінансів показує, що вже створено всі необхідні формалізми для моделювання фінансових систем, проте нинішній рівень модельних уявлень відстає від запитів практики фінансового менеджменту. Нечіткі множини практично не застосовувалися до теперішнього часу для фінансового аналізу і планування корпорацій, оцінки інвестиційної привабливості цінних паперів, для оптимізації фондового портфеля і прогнозування [5].
Розглядаючи роль нечітко-множинних описів для фінансового моделювання, в роботі зазначається, що такі моделі і методи на їх основі є законними правоприемниками імовірнісних моделей і методів, з одного боку, та експертних методів, з іншого боку. Взаємозв'язок класичних імовірнісних, експертних та нечітко-множинних описів представлений на рисунку 1:
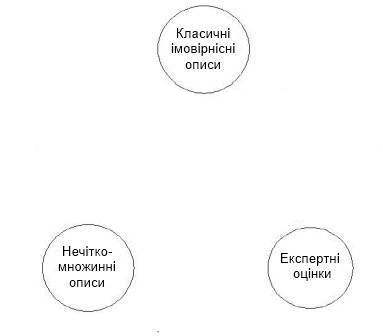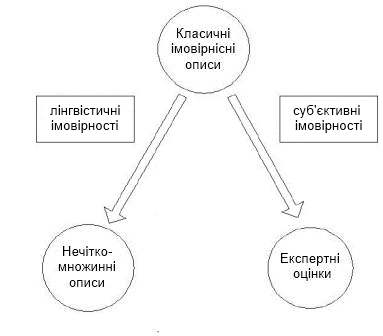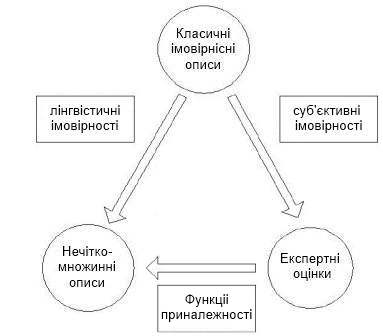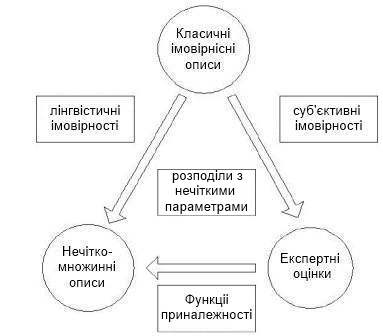
Рисунок
1 – Взаємозалежність класичних
імовірностних, експертних та нечітко-множинних методів оцінювання
(анимація: 4 кадрів, 6 циклів повторень, 111 килобайт)
Модель Альтмана побудована з використанням експертного апарату мультиплікативного дискримінантного аналізу (МДА), який дозволяє підібрати такі показники, дисперсія яких між групами була б максимальною, а всередині групи мінімальною. В результаті МДА побудована модель Альтмана (Z-рахунок), що має наступний вигляд:

де K1 = власний оборотний капітал /сума активів;
K2 = перерозподілу прибутків /сума активів;
K3 = прибуток до сплати відсотків /сума активів;
K4 = ринкова вартість власного капіталу /вартість позикового капіталу;
K5 = обсяг продажів /сума активів;
У результаті підрахунку Z – показника для конкретного підприємства робиться висновок:
якщо Z <1,81 – дуже висока ймовірність банкрутства;
якщо 1,81 < Z < 2,7 – висока ймовірність банкрутства;
якщо 2,7 < Z < 2,99 – можливе банкрутство;
якщо Z > 30 – ймовірність банкрутства вкрай мала.
В економіці України модель Альтмана поки не отримала широкого застосування з наступних причин [2]:
- Потрібно обчислення відповідних коефіцієнтів при показниках Ki, i = 1..5, які відрізняються від їх значень для зарубіжних країн;
- Інформація про фінансовий стан аналізованих підприємств, як правило, недостовірна, керівництво ряду підприємств "свідомо" підправляє свої показники у фінансових звітах, що робить неможливим знайти достовірні оцінки коефіцієнтів в Z-моделі.
Тому завдання оцінки ймовірності ризику банкрутства повинна вирішуватися в умовах невизначеності, неповноти вихідної інформації, і для її вирішення пропонується використовувати адекватний апарат прийняття рішень – нечіткі множини і нечіткі нейронні мережі (ННС). Розглянемо матричний метод прогнозування банкрутства корпорацій запропонований доктором економічних наук О.А. Недосекіним [1].
- Експерт будує лінгвістичну змінну зі своїм терм-множиною значень. Наприклад, "Рівень менеджменту" може мати наступне терм-безліч значень: "Дуже низький, Низький, Середній, Високий, Дуже високий" [1].
- Для того, щоб конструктивно описати лінгвістичну змінну, експерт вибирає відповідний кількісний ознака наприклад, сконструйований спеціальним чином показник рівня менеджменту, який приймає значення від нуля до одиниці [1].
- Далі експерт кожному значенню лінгвістичної змінної яка з побудови є нечітким підмножиною значень інтервалу [0,1], ставить у відповідність функцію приналежності того чи іншого нечткого множини. Як правило, це трапецеїдальний функція приналежності [1]. Верхній підставі трапеції відповідає повній впевненості експерта в правильності класифікації, а нижнє – впевненості в тому, що ніякі інші значення інтервалу [0,1] не потрапляють в вибрану нечітку безліч. (Див. рис.2.)
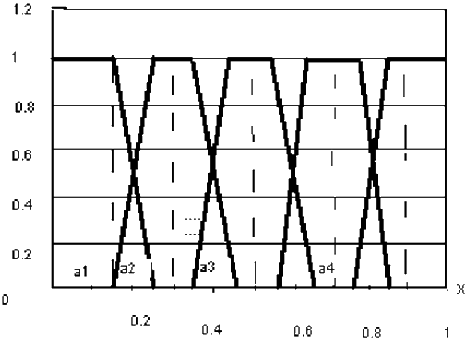
Рисунок 2 – Трапецевидна функція приналежності
На цьому опис лінгвістичних змінних закінчується. Нечітко-множинний метод, відомий також, як матричний метод, складається з наступних етапів:
Етап 1 (Лінгвістичні змінні і нечіткі множини). Лінгвістична змінна Е "Стан підприємства" має п'ять значень:
E1 – нечітке підмножина станів "граничного неблагополуччя";
E2 – нечітке підмножина станів "неблагополуччя";
E3 – нечітке підмножина станів "середнього рівня";
E4 – нечітке підмножина станів "відносного благополуччя";
E5 – нечітке підмножина станів "граничне благополуччя".
Відповідна змінної E лінгвістична змінна G "Ризик банкрутства" також має 5 значень:
G1 – нечітке підмножина станів "граничний ризик банкрутства";
G2 – нечітке підмножина станів "ступінь ризику банкрутства висока";
G3 – нечітке підмножина станів "ступінь ризику банкрутства середня";
G4 – нечітке підмножина станів "низька ступінь ризику банкрутства";
G5 – нечітке підмножина станів "ризик банкрутства незначний".
Носій безлічі G – показник ступеня ризику банкрутства g – приймає значення від нуля до одиниці за визначенням.
Для окремого фінансового показника або показника управління Хi задаємо лінгвістичну змінну Вi "рівень показника Хi" на наступному терм-множині значень:
Bi1 – підмножина "дуже низький рівень показника Хi";
Bi2 – підмножина "низький рівень показника Хi";
Bi3 – підмножина "середній рівень показника Хi";
Bi4 – підмножина "високий рівень показника Хi";
Bi5 – підмножина "дуже високий рівень показника Хi".
Етап 2 (Показники). Побудуємо набір окремих показників X = {Хi} загальним числом N, які на думку експерта, з одного боку впливають на оцінку ризику банкрутства підприємства, а з іншого боку, оцінюють різні за природою боку ділової та фінансової життя підприємства. Наприклад, в матричному методі використовуються такі показники [8]:
Х1 – коефіцієнт автономії (відношення власного капіталу до валюти балансу);
Х2 – коефіцієнт забезпечення оборотних активів власними коштами (відношення чистого оборотного капіталу до оборотних активів);
Х3 – коефіцієнт проміжної ліквідності (відношення суми грошових коштів і дебіторської заборгованості до короткострокових пасивів);
Х4 – коефіцієнт абсолютної ліквідності (відношення суми грошових коштів до короткострокових пасивів);
Х5 – оборотність всіх активів за рік (відношення виручки від реалізації послуг до середньої виручці за період вартості активів);
Х6 – рентабельність всього капіталу (відношення чистого прибутку до середньої за період вартості активів).
Етап 3 (Значимість показників). Поставимо у відповідність кожному показнику Хi рівень його значущості ri. Для того, щоб оцінити цей рівень, необхідно поставити всі показники по порядку зменшення їх значимості так, щоб виконувалася співвідношення [2]:
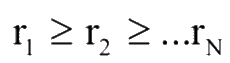
Якщо система показників проранжірованна у порядку зменшення їх значимості, то вага i-го показника ri необхідно визначати за правилом Фішберна:

Етап 4 (Класифікація ступеня ризику). Побудуємо класифікацію поточного значення g показника ступеня ризику як критерій розбиття цієї множини на нечіткі підмножини (таблиця 1) [1]:
Таблиця 1. Класифікація ступеню ризику
| Інтервал значень g | Класификація рівня параметра | Складність оцінки впевненності (функція приналежності) |
| 0<g<0.15 | G5 | 1 |
| 0.15<g<0.25 | G5 | m5 = 10*(0.25 – g) |
| G4 | 1 – m5 = m4 | |
| 0.25<g<0.35 | G4 | 1 |
| 0.35<g<0.45 | G4 | m4 = 10*(0.45 – g) |
| G3 | 1 – m4 = m3 | |
| 0.45<g<0.55 | G3 | 1 |
| 0.55<g<0.65 | G3 | m3 = 10*(0.65 – g) |
| G2 | 1 – m3 = m2 | |
| 0.65<g<0.75 | G2 | 1 |
| 0.75<g<0.85 | G2 | m2 = 10*(0.85 – g) |
| G1 | 1 – m2 = m1 | |
| 0.85<g<1 | G1 | 1 |
Етап 5 (Класифікація значень показників). Побудуємо класифікацію поточних значень показників Х як критерій розбиття повного безлічі їх значень на нечіткі підмножини виду В. Один із прикладів такої класифікації наведено нижче. У клітинах таблиці стоять трапецеїдальні нечіткі числа, які характеризують відповідні функції приналежності.
Етап 6 (Оцінка рівня показників). Проведемо оцінку поточного рівня показників і зведемо отримані результати в таблицю 2.
Таблиця 2. Поточні значення показників
| Показатель | Текущее значение |
| X1 | x1 |
| .... | .... |
| Xi | xi |
| .... | .... |
| XN | xN |
Етап 7 (Класифікація рівня показників). Проведемо класифікацію поточних значень х за умовою таблиці, побудованої на етапі 5. Результатом проведеної класифікації є таблиця значень рівнів належності носія хi нечітким підмножини В j.
Етап 8 (Оцінка ступеня ризику). Виконаємо обчислювальні операції для оцінки ступеня ризику банкрутства g [2].

Далі рівень отриманого комплексного показника проходить розпізнавання по простому правилу або на основі системи трапецієподібних функцій належності. Зокрема, просте правило:
g: [0, 0.2] – дуже низький рівень фінансового стану;
g: [0.21, 0.4] – низький рівень фінансового стану;
g: [0.41, 0.6] – середній рівень фінансового стану;
g: [0.61, 0.8] – високий рівень фінансового стану;
g: [0.81, 1] – дуже високий рівень фінансового стану.
Побудований метод комплексного аналізу фінансового стану корпорації може бути з успіхом застосований в бізнес-процесі щоквартального моніторингу стану корпорації за даними її фінансової звітності.
Висновки
Побудований метод комплексного аналізу фінансового стану корпорації може бути з успіхом застосований в бізнес-процесі щоквартального моніторингу стану корпорації за даними її фінансової звітності. Організовані у вигляді окремих, цілісних структур інформаційного забезпечення знання про предметної області стають явними і відокремлюються від інших типів знань, наприклад загальних знань. Бази знань дозволяють робити висновки спираюся не тільки на методи формальної (математичної) логіки, а й на основі досвіду, фактів, евристик, тобто вони найбільш наближені до людської логіки. Розробки в галузі штучного інтелекту мають на меті використання великих обсягів високоякісних спеціальних знань про деяку вузької предметної області для вирішення складних, неординарних завдань.
База знань є основою експертної системи, вона накопичується в процесі її побудови. Володіння виражаються в явному вигляді, що дозволяє зробити явним спосіб мислення та вирішення завдань, і організовані так, щоб спростити ухвалення рішень. База знань, обумовлює компетентність експертної системи, втілює в собі знання фахівців установи, отд їла, досвід групи фахівців і є інституційним знань.
При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: січень 2014 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після вказаної дати.
Перелік посилань
- Недосекин А.О. Методологические основы моделирования финансовой деятельности с использованием нечетко-множественных описаний. /Диссертация на соискание ученой степени доктора экономических наук. – Спб.: Санкт-Петербургский государственный университет экономики и финансов, 2003. – 280 с.
- Лузин В.П. Информационно-технические основы создания системы управления крупными рисками в страховой компании. – М.: БУКВИЦА, 2009 – 146 с.
- Штовба С.Д. Проектирование нечетких систем средствами Matlab.– М.: Горячая линия, 2007.
- Гутко Л.М. Страховий ринок Украхни: Стан, проблеми розвитку та шляхи їх вирішення//Менеджент: Оцінка страхового ризику №4, – 2009 рік.
- Экономико-математические методы и прикладные модели: Учебное пособие для вузов/ В.В. Федосеев, А.Н. Гармаш, И.В. Орлова и др. – М.: ЮНИТИ-ДАНА, 2005.
- Тэрано, Т., Асаи, К., Сугэно, М. Прикладные нёчеткие системы. М.: Мир, 1993. 368c.
- Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений. М.: Мир, 1976. 166c.
- Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы. – М., 2004.
- Круглов В.В., Дли М.И. Интеллектуальные информационные системы: компьютерная поддержка систем нечеткой логики и нечеткого вывода. – М.: Физматлит, 2002.
- Ротштейн А. П. Интеллектуальные технологии идентификации: нечёткая логика, генетические алгоритмы, нейронные сети / А. П. Ротштейн. – Винница: УНИВЕРСУМ-Винница, 1999. – 320 с.
