Abstract
Content
- Introduction
- 1. Theme urgency
- 2. Goal and tasks of the research
- 3. Fuzzy multiple analysis of risk bankruptcy
- Conclusion
- References
Introduction
Accurate measurement of risk is different quantitative methods: mathematical, statistical, methods of probability theory, game theory, and more. etc. Risk Insurance escorted large measure of uncertainty, the lack of severe laws and can not set the precise numerical data. These factors limit the use of classical methods of statistical analysis, and there is a need to develop new methods of evaluation, which may include systems with fuzzy logic.
1. Theme urgency
Background research determined the need for timely detection of adverse trends in the insurance company in according to the methods of fuzzy logic. Easy of fuzzy logic as a problem-solving methodology ensures its successful use in embedded system control and analysis.
2. Goal and tasks of the research
Purpose of the magister's work – to form an integrated approach to the assessment of risk of bankruptcy of the insurance company.
The object of study – the risk of bankruptcy of the insurance company.
The subject of the study – the study of the relationship between qualitative variables and the magnitude of the risk of bankruptcy.
Research objectives:
Consider the theoretical aspects of risk analysis;
Identify the relationship between indicators of the functioning of the insurance company and the risk of bankruptcy;
Measure the risk of bankruptcy in quantitative terms.
The method of research – the application of the method of fuzzy logic, through the creation of a knowledge base, which is an expert system.
3. Fuzzy multiple analysis of risk bankruptcy
Consider the matrix method for predicting corporate bankruptcy proposed by doctor of economic sciences Nedosekin. Judge builds a linguistic variable with its term-set values.In order to constructively describe linguistic variable, the expert selects the appropriate quantitative trait – for example, a specially designed indicator of the level of management, which takes values from zero to one. Next to each value of expert linguistic variable is by construction a fuzzy subset of the values on interval [0,1] assigns a membership function of a fuzzy set. Typically, this is a trapezoidal membership function [1].
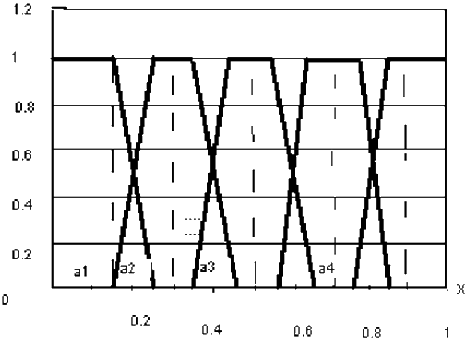
Figure 1 – Trapezoidal membership function
This completes the description of linguistic variables ends. Fuzzy-multiple method, also known as the matrix method consists of the following steps:
Phase 1 (linguistic variables and fuzzy sets) Linguistic variable E "State enterprise" has five values The corresponding variable E linguistic variable G "The risk of bankruptcy". For a financial index or index management Xi Bi ask the linguistic variable "level indicator Xi" [3].
Step 2 (Performance). Construct a set of individual indicators X = {Xi} the total number N, which in his opinion, on the one hand affect the assessment of the risk of bankruptcy, and on the other hand, evaluate different in nature by business and financial enterprise.
Stage 3 (The significance of indicators). We assign to each indicator Xi level of significance ri. In order to evaluate this level, you need to put all the parameters in order to reduce their significance so as to satisfy the relation [4]:
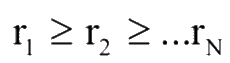
Stage 4 (Classification of risk). Need to construct a classification of the current value of g as a measure of risk criteria to split this set into fuzzy subsets.
Step 5 (Evaluation of the performance). Carried out to assess the current level of performance.
Step 6 (classification level indicators). A classification of the current values of X byassesing the level of performance. The result of the classification is carried out by a table of values membership levels carier Xi fuzzy subset Vj.
Step 7 (Risk Assessment). Computational operations are performed to assess the degree of risk of bankruptcy g image Next, the resulting level of the complex index of recognition passed by a simple rule-based system or trapezoidal membership functions. In particular, a simple rule [1]:
g: [0, 0.2] – a very low level of financial condition;
g: [0.21, 0.4]– low level of financial condition;
g: [0.41, 0.6] – the average level of financial condition;
g: [0.61, 0.8] – a high level of financial condition;
g: [0.81, 1] – a very high level of financial performance.
Conclusion
QMethod constructed a comprehensive analysis of the financial condition of the corporation may be successfully applied in the business process of the quarterly monitoring of the corporation according to its financial statements. Arranged in the form of individual, holistic information management structures domain knowledge becomes explicit and separated from other types of knowledge, such as general knowledge. Knowledge base allows to draw conclusions not only rely on formal methods (mathematical) logic, but on the basis of experience, facts, heuristics, ie they are closest to human logic. Developments in the field of artificial intelligence have to use large amounts of high-quality special knowledge about a narrow subject area for the solution of complex, unusual problems.
This master's work is not completed yet. Final completion: January 2014. The full text of the work and materials on the topic can be obtained from the author or his head after this date.
References
- Недосекин А.О. Методологические основы моделирования финансовой деятельности с использованием нечетко-множественных описаний. /Диссертация на соискание ученой степени доктора экономических наук. – Спб.:Санкт-Петербургский государственный университет экономики и финансов, 2003. – 280 с.
- Лузин В.П. Информационно-технические основы создания системы управления крупными рисками в страховой компании. – М.: БУКВИЦА, 2009 – 146 с.
- Штовба С.Д. Проектирование нечетких систем средствами Matlab.– М.: Горячая линия, 2007.
- Гутко Л.М. Страховий ринок Украхни: Стан, проблеми розвитку та шляхи їх вирішення//Менеджент: Оцінка страхового ризику №4,-2009 рік.
- Экономико-математические методы и прикладные модели: Учебное пособие для вузов/ В.В. Федосеев, А.Н. Гармаш, И.В. Орлова и др. – М.: ЮНИТИ-ДАНА, 2005.
- Тэрано, Т.; Асаи, К.; Сугэно, М. Прикладные нёчеткие системы. М.: Мир, 1993. 368c.
- Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений. М.: Мир, 1976. 166c.
- Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы. – М., 2004.
- Круглов В.В., Дли М.И. Интеллектуальные информационные системы: компьютерная поддержка систем нечеткой логики и нечеткого вывода. – М.: Физматлит, 2002.
- Ротштейн А. П. Интеллектуальные технологии идентификации: нечёткая логика, генетические алгоритмы, нейронные сети / А. П. Ротштейн. – Винница: УНИВЕРСУМ-Винница, 1999. – 320 с.
