Реферат по теме выпускной работы
Содержание
- Введение
- 1. Анализ объекта регулирования
- 2. Анализ типовой двухканальной системы подчиненного регулирования скорости
- 3. Синтез и анализ двухканальной системы подчиненного регулирования скорости с дополнительными обратными связями по разности скоростей сосредоточенных масс
- Выводы
- Список литературы
Введение
Для перемещения грузов в промышленных условиях широко применяются мостовые краны, представляющие собой совокупность трех основных механизмов:
- моста, передвигающегося по рельсам, уложенным на подкрановые балки вдоль пролета открытой или закрытой грузовой площадки;
- тележки с подвешенным к ней грузом, перемещающейся вдоль моста, т.е. поперек пролета площадки;
- подъемного устройства в виде лебедки для намотки каната, к которому прикреплен транспортируемый груз.
Пролет моста для большинства кранов составляет от 10,5 м до 34,5 м (с шагом 3 м). Поэтому при перемещении моста и тележки главные балки моста, имеющие большую длину при сравнительно небольшом поперечном сечении, совершают упругие колебания в разных направлениях, вызывающие повышенный износ металлоконструкций и механизмов.
Проблеме исследования вертикальных колебаний конструкции мостового крана посвящено большое количество работ [2, 3, 5]. Действительно, колебания в этом направлении имеют самую большую амплитуду и негативно виляют не только на мост, но также и на канат, который с учетом его собственной упругости, постепенно утрачивает свою прочность. Тем не менее, упругость конструкции в горизонтальном направлении, проявляющаяся преимущественно при перемещении моста, даже при сравнительно небольших деформациях приводит к возникновению больших упругих усилий, воздействующих на конструкцию моста. Это вызывает накопление усталости металла и может привести к механическим поломкам. Таким образом, гашение поперечных колебаний конструкции мостового крана является актуальной задачей, решению которой уделено не достаточно внимания.
Решить эту задачу можно, управляя соответствующим образом электроприводами колес моста. Однако при этом необходимо следить, чтобы гашение колебаний не сопровождалось перекосом моста в поперечном направлении, так как при этом к колесам и приводным валам прикладываются значительные по величине изгибающие моменты.
Рассматривая упругие колебания мостового крана, необходимо представлять его конструкцию как систему с распределенными параметрами. Однако создание математического описания такой системы является довольно сложной задачей. К тому же по математической модели такой системы затруднительно проводить синтез регуляторов. Поэтому при рассмотрении систем с распределенными параметрами применяют различные методы упрощения модели объекта. В случае механических объектов наиболее часто распределенные массы и упругости заменяют сосредоточенными, представляя математическую модель объекта в виде многомассовой системы.
Точность полученных таким образом линейных математических моделей зависит от того, насколько адекватно выполнен переход от модели с распределенными параметрами к модели с сосредоточенными параметрами. Некоторые авторы [6, 8] рассматривают мост как невесомую упругую связь, равномерно распределяя его массу между колесами и фиксируя тележку в одном из крайних положений или пренебрегая ее массой, что является очень грубым допущением.
В [2] разработана линейная математическая модель мостового крана с тележкой, расположенной в средней части моста. При одинаковых массах колес моста и упругостях его частей справа и слева от тележки мост с тележкой представлен в виде двухмассовой системы, в которой колеса моста объединены в одну массу. Адекватность двухмассовой модели оценивалась путем сравнения ее с виртуальной механической моделью в среде пакета Comsol, в которой расчет переходных процессов выполняется методом конечных элементов. В основу выбора параметров этой модели было положено равенство амплитуд колебаний балки с двумя закрепленными концами и грузом, расположенным в ее центре совпадает с амплитудой колебаний груза, расположенного на невесомой балке, если к массе балки добавить 17/35≈0.5 массы балки. Оказалось, что наибольшее совпадение амплитуд колебаний сосредоточенных масс при заданной их частоте в модели с сосредоточенными параметрами и соответствующих их расположению точек металлической конструкции в модели с распределенными параметрами достигается при выполнении условия:

где mc1,3 — сосредоточенные массы первой и второй опор соответственно, которые включают в себя массу колес, электроприводов и концевых балок, mp — распределенная масса главных балок моста, mcT — сосредоточенная масса тележки. Коэффициент жесткости единственной в этом случае упругой связи можно легко рассчитать, зная частоту упругих колебаний и сосредоточенные массы.
Значительно более сложным является случай, когда тележка смещена относительно центральной точки моста. При этом упругости частей балок моста, слева и справа от тележки, будут отличаться друг от друга. Кроме того, закон распределения массы моста между его колесами и тележкой в функции положения тележки не известен. Тем не менее, в [4] на основании анализа колебаний моста в точке расположения тележки, выполненного в пакете Comsol, обоснована возможность представления моста с тележкой, установленной в точке моста, отличной от его центра, в виде трехмассовой системы, представленной на рис.1, и определены параметры такой линейной модели для некоторых фиксированных положений тележки, из условия максимального сходства переходных процессов (частот и амплитуд упругих колебаний).
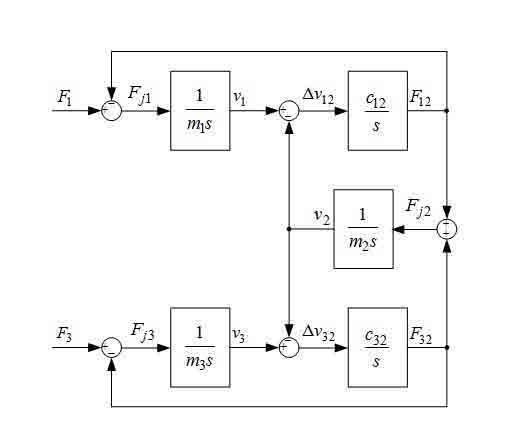
Рисунок 1 — Структурная схема трехмассовой системы
Целью работы является синтез взаимосвязанной двухканальной системы регулирования скоростью колес, способной подавить поперечные колебания моста без его существенного перекоса, на основе предложенной модели.
1. Анализ объекта регулирования
Прежде всего, исследуем объект регулирования. Модель рис.1 имеет характеристический полином:
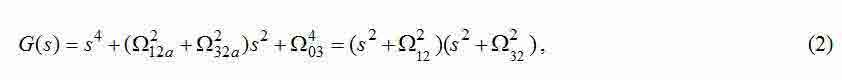
где
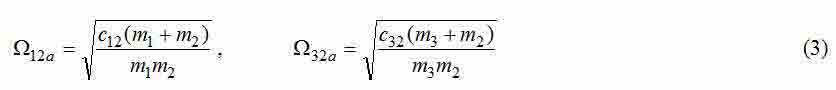
— частоты собственных упругих колебаний автономных двухмассовых систем 12 и 23;
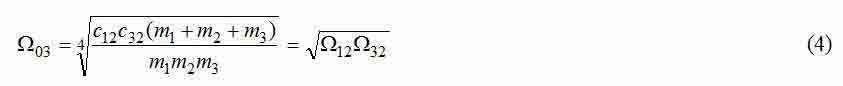
— среднегеометрический корень характеристического полинома рассматриваемой трехмассовой системы;
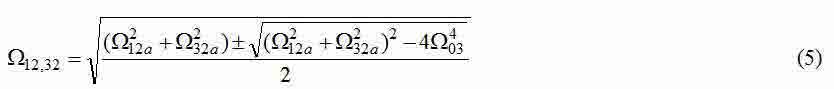
— частоты собственных упругих колебаний трехмассовой системы.
Передаточные функции (ПФ) от входных сил до динамического усилия, воздействующего на вторую массу, имеют вид:
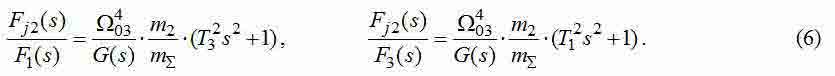
где

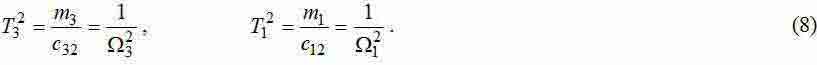
Разложением полученных ПФ на сумму дробей при равенстве приложенных к колесам сил (F1+F2=F) получим выражения для амплитуд каждой из гармоник:
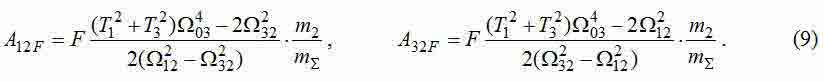
Полученные формулы для частот и амплитуд колебаний трехмассовой системы могут быть использованы для определения параметров модели. Желаемые численные значения частот и амплитуд можно получить путем анализа Фурье результатов моделирования моста в пакете Comsol. Учитывая, что в этой программной среде удобно измерять скорости перемещения разных точек моста, а не их ускорения, то из амплитуд колебаний упругого усилия (8) необходимо определить амплитуды колебаний скорости:
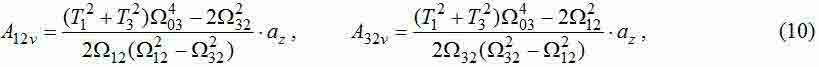
где  — задание на ускорение моста.
— задание на ускорение моста.
Приравнивая выражения (5) и (10) к соответствующим значениям, найденным в результате спектрального анализа, и добавляя к полученным таким способом 4-м уравнениям уравнение (7), получаем систему 5 нелинейных уравнений с 5-ю неизвестными: [m1, m2, m3, c12, c32], которую можно решить численными методами.
Как уже отмечалось ранее, рассматриваемый объект регулирования (ОР) имеет переменные параметры. Рассмотрим некоторые частные случаи, при которых изменение параметров приводит к редуцированию ОР.
При расположении тележки в центре моста:
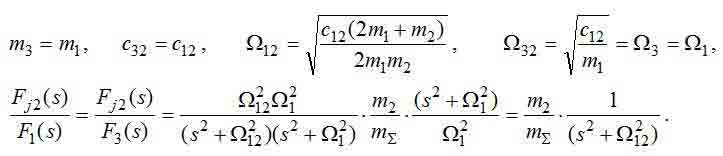
2. Анализ типовой двухканальной системы подчиненного регулирования скорости
Имея приближенную линейную модель объекта регулирования, можно приступить к синтезу системы автоматического управления (САУ).
В простейшем случае для управления приводами колес моста применяют систему подчиненного регулирования скорости (СПРС), представленную на рис.2, без корректирующих связей, обозначенных пунктирами. На этом рисунке контуры токов (усилий) двигателей представлены упрощенно в виде апериодических звеньев с малыми постоянными времени TT. Переходные процессы, полученные при моделировании такой системы для случая расположения тележки на расстоянии l=8 m от левого края моста, где условно расположена сосредоточенная масса m1 при длине моста L=20 м показаны на рис.2. Они получены при TT=4 mc и Tc1=Tc2=2TT На этих графиках видны медленно затухающие упругие колебания в сигналах сил и скоростей, уменьшить которые можно путем снижения коэффициентов усиления регуляторов скорости и дополнения системы управления корректирующими обратными связями по разностям скоростей Δv12 и Δv32 заведенными на входы регуляторов скорости, ка к это показано на рис.3.
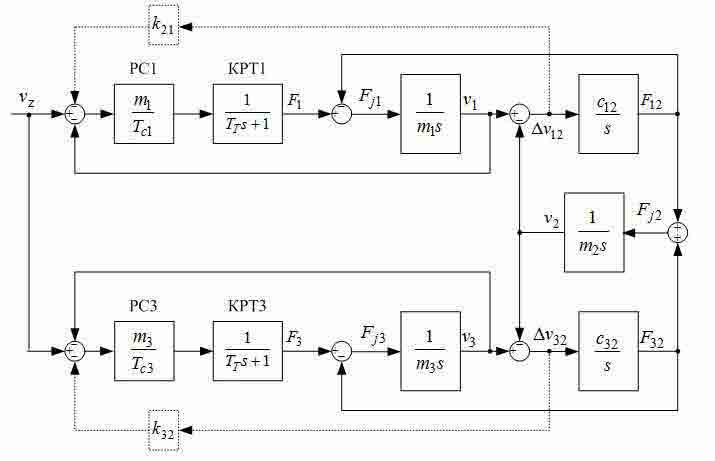
Рисунок 2 — Структурная схема системы подчиненного регулирования скорости трехмассового объекта.
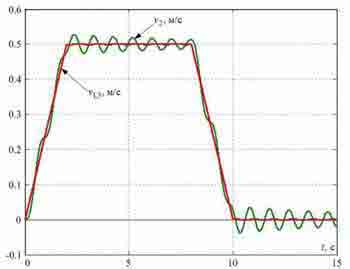
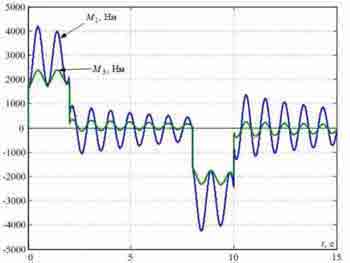
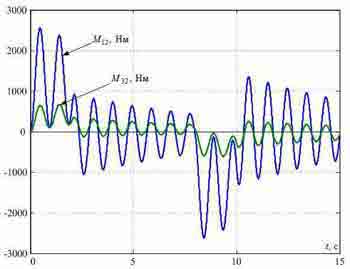
Рисунок 3 — Переходные процессы в типовой СПРС, синтезированной без учета упругости металлических конструкций.
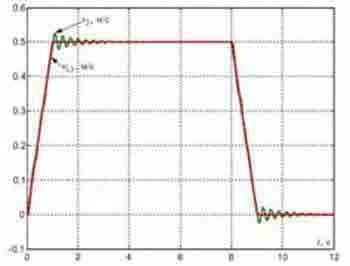
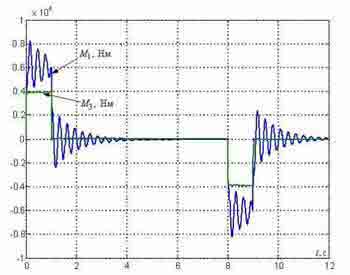
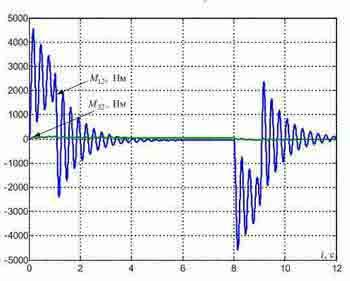
Рисунок 4 — Переходные процессы в типовой СПРС, синтезированной c учетом упругости металлических конструкций.
3. Синтез и анализ двухканальной системы подчиненного регулирования скорости с дополнительными обратными связями по разности скоростей сосредоточенных масс
Формулы для расчета постоянной времени интегрирования контура скорости и корректирующего коэффициента по разности скоростей первой и второй сосредоточенных масс выведены для системы управления двухмассовым объектом на основании анализа диаграмм Вышнеградского [1] и из условий модульного оптимума (МО) [2].
Используем методику [2] для параметрического синтеза системы рис.2. Для этого необходимо найти ее передаточную функцию от задания на скорость до скорости второй массы. Как показано в работах [1, 2], при ее выводе можно пренебречь инерционностью быстродействующего контура тока. Такая ПФ имеет вид:
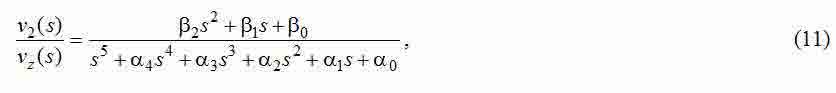
где

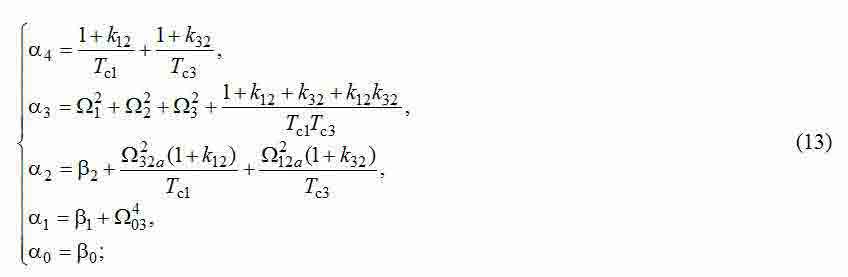
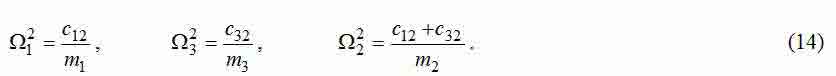
Для выведенной передаточной функции составляем уравнения, обеспечивающее достижение МО [3, 4]. Чтобы определить как неизвестные постоянные времени Tc1, Tc3, так и коэффициенты корректирующих обратных связей κ12, κ32, необходимо решить систему 4-х уравнений с 4-мя неизвестными:

Для синтеза СПРС без дополнительных корректирующих связей необходимо в формулах (12), (13) положить κ12=0, κ32=0 и для полученных таким образом полиномиальных коэффициентов решить совместно два первых уравнения системы (15) относительно Tc1, Tc3, Результаты моделирования показали, что, как и для двухмассовых систем, при отсутствии корректирующих обратных связей по разностям скоростей амплитуда и время затухания упругих колебаний уменьшаются не достаточно эффективно. Поэтому остановимся на исследовании СПРС с дополнительными связями.
К сожалению, аналитическое решение уравнений оптимизации для рассматриваемой системы получить не удалось, но численные решения определяются без особых проблем. Начинать процесс параметрического синтеза следует с размещения тележки в центре моста, когда трехмассовая система вырождается в двухмассовую за счет того, что m1=m3 и c12=m32 Параметры САУ в этом случае можно вычислить по формулам, взятым из [8] и несколько преобразованным с учетом особенностей двухмассовой модели и необходимости последующего перехода к представленной трехмассовой модели:
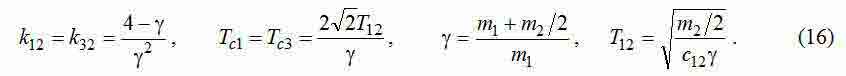
Параметры САУ при расположении тележки не в центре моста следует определять решением системы уравнений (15) с коэффициентами (12), (13). Для обеспечения хорошей сходимости итерационного вычислительного процесса целесообразно дискретно, с некоторым шагом, перемещать тележку от центра моста к одному из его колес. В качестве начальных приближений параметров САУ всякий раз следует в качестве начальных приближений параметров использовать их значения, полученные на предыдущем шаге.
Переходные процессы в синтезированной СПРС при Δl=2 м показаны на рис. 5. Они демонстрируют эффективность гашения упругих колебаний рассматриваемых точек моста предложенным методом.
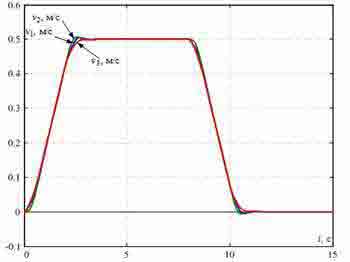
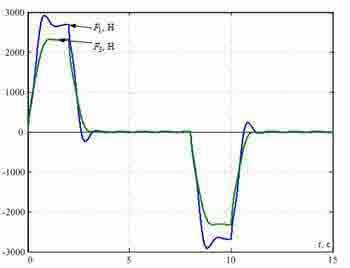
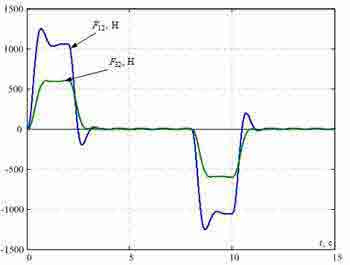
Рисунок 5 — Переходные процессы в системе подчиненного регулирования, синтезированной из условий модульного оптимума.
Для сравнения динамических свойств разработанной САУ при разных положениях тележки на рис.6 приведены графики изменения ускорения второй массы. Из них видно, что при изменении Δl от 1м до 6 м быстродействие синтезированной системы повышается, а характер изменения рассматриваемого сигнала остается практически неизменным. Перерегулирование переходной функции составляет 10%. Поведение ускорения второй массы при расположении тележки в центре моста выпадает из общего ряда, т.к. характеризуется меньшим перерегулированием (8%) и более высоким быстродействием. Это объясняется тем, что параметры САУ в этом случае рассчитывались из других уравнений оптимизации, выведенных для двухмассовой системы, передаточная функция которой имеет характеристический полином второго порядка и полином воздействия нулевого порядка.
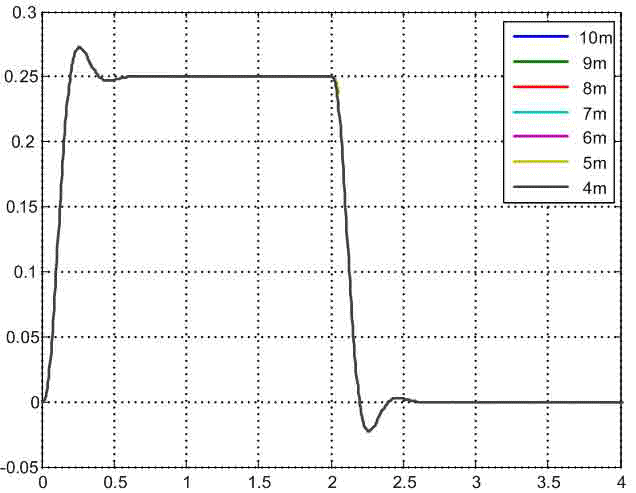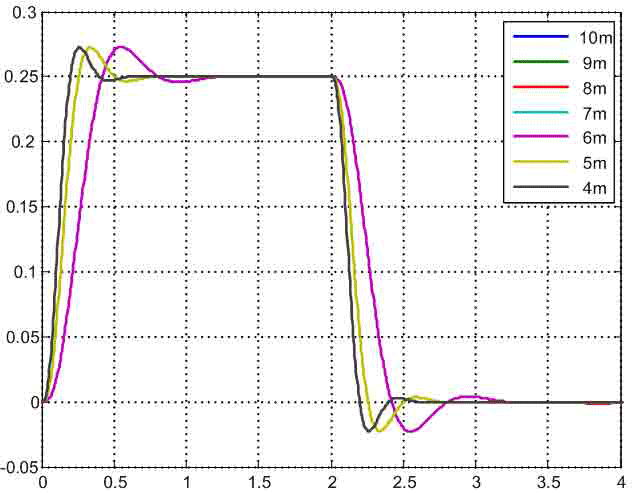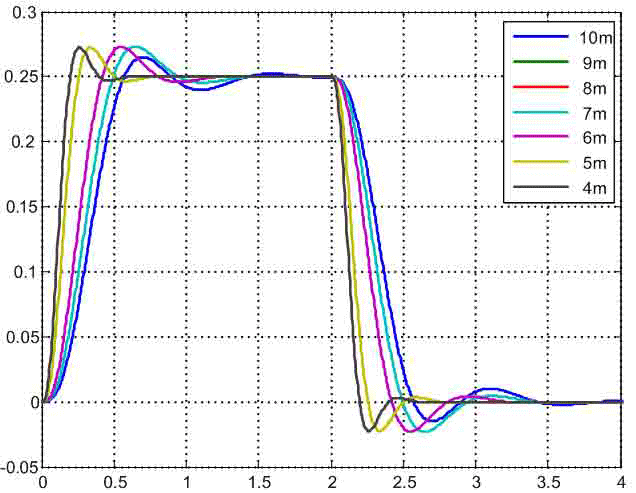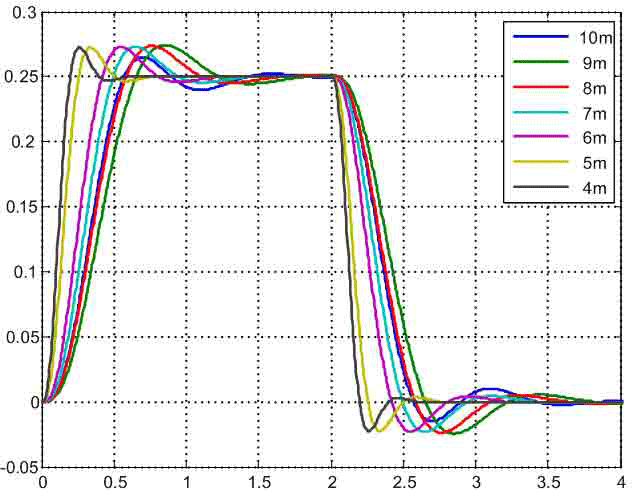
Рисунок 6 — Графики изменения ускорения второй массы,
(анимация: 7 кадров, 7 циклов повторения, 183 килобайт)
Выводы
- СПРС, синтезированная без учета упругих связей демпфирует колебания очень слабо;
- СПРС с дополнительными корректирующими связями по разности скоростей эффективно гасит упругие колебания, хотя и отличается несколько повышенным перерегулированием по суммарному упругому моменту и наличием небольшого перерегулирования по скоростям. Основным преимуществом этой системы является простота ее реализации, т.к. все сигналы обратных связей легко измеряются;
- Предложенные системы управления с постоянными параметрами демпфируют упругие колебания только при фиксированном положении тележки. В дальнейшем необходимо разработать адаптивную САУ, осуществляющую подавление колебаний при движении тележки по мосту.
Примечание. При написании данного реферата дипломная работа находится на стадии выполнения, поэтому приведенный реферат содержит имеющиеся на момент сдачи экзамена по дисциплине «Интернет-технологии» информацию. Конечный срок выполнения магистерской работы и дата защиты диплома – январь 2015 года.
Список источников
- Борцов Ю.А., Соколовский Г.Г. Автоматизированный электропривод с упругими связями. – СПб.: Энергоатомиздат, 1992. – 288 с.
- Коцегуб П.Х., Баринберг В.А., Толочко О.И., Федоряк Р.В. Оптимизация двухмассовых систем регулирования скорости // Известия вузов. Электромеханика. – 1998. – №4. – С. 54-57.
- Kessler C. Uber die Vorausberechnung optimal abgestimmer Regelkreise // Regelungstechnik. 1955. – №1. – S. 16-22, №2. – S. 40-49.
- Коцегуб П.Х., Толочко О.И. Оптимизация систем управления по модулю амплитудно-частотной характеристики // Изв. вузов. Электромеханика. – 1977. – №6. – С. 679-684.
- Толочко О.І., Коцегуб П.Х., Федоряк Р.В. Дослідження впливу середньогеометрічного кореня характеристичного полінома на властивості системи модального керування двомасовим електромеханічним об‘єктом // Наукові праці ДонДТУ. Серія „Електротехніка і енергетика”. – Донецьк: ДонДТУ. – 2002. – №41. – С. 146-155.
- Бургин Б.Ш. Анализ и синтез двухмассовых электромеханических систем. – Новосибирск: Новосиб. электротехн. ин-т, 1992. – 199 с.
- Александров Е.Е., Кузнецов Б.И., Радиевский А.Е., Тернюк Н.Э. Оптимизация электромеханических систем с упругими связями. – Харьков: IMIC, 1995. – 304 с.
- Тарарыкин С.В., Тютиков В.В. Проектирование регуляторов состояния упругих электромеханических систем // Электричество. – 1998. – №3. – С. 52-57.
- Герасимяк Р.П., Ант А.М., Рамарувахуака А.М. Синтез электромеханической системы подъемных механизмов с подавлением упругих колебаний // Електромашинобудування та електрообладнання. – 1996. – № 48.
- Герасимяк Р.П., Рамарувахуака А.М. Система управления электропривода двухмассовой электромеханической системой // Электротехника. – 1998. – №6. – С. 28-31.
- Коцегуб П.Х., Толочко О.И., Федоряк Р.В. Практическая реализация цифровых САУ в среде пакета Матлаб с использованием платформы реального времени „QNX TARGET” // Вісник Національного технічного університету „ХПІ”. – Харків: НТУ ХПІ. – 2002. – Т.1, №12.– С. 98-101.
- Real-TimeWorkshop. For Use with Simulink. User’s Guide. The MathWorks Inc., 2000. – 622 p.
