Реферат з теми випускної роботи
Зміст
- Вступ
- 1. Аналіз об'єкта регулювання
- 2. Аналіз типової двоканальної системи підпорядкованого регулювання швидкості
- 3. Синтез і аналіз двоканальної системи підпорядкованого регулювання швидкості з додатковими зворотними зв'язками по різниці швидкостей зосереджених мас
- Висновки
- Список літератури
Вступ
Для переміщення вантажів у промислових умовах широко застосовуються мостові крани, які становлять сукупність трьох основних механізмів:
- моста, що пересувається по рейках, укладених на підкранові балки уздовж прольоту відкритої або закритої вантажної площадки;
- візка з підвішеним до неї вантажем, що переміщається уздовж моста, тобто поперек прольоту площадки;
- підйомного пристрою у вигляді лебідки для намотування каната, до якого прикріплений вантаж, який транспортується.
Проліт моста для більшості кранів складає від 10,5 м до 34,5 м (з кроком 3 м). Тому при переміщенні моста і візка головні балки моста, що мають велику довжину при порівняно невеликому поперечному перерізі, здійснюють пружні коливання в різних напрямках, що викликають підвищений знос металоконструкцій і механізмів.
Проблемі дослідження вертикальних коливань конструкції мостового крана присвячена велика кількість робіт [2, 3, 5]. Дійсно, коливання в цьому напрямку мають найбільшу амплітуду і негативно впливають не тільки на міст, але також і на канат, який з урахуванням його власної пружності, поступово втрачає свою міцність. Проте, пружність конструкції в горизонтальному напрямку, що виявляється переважно при переміщенні моста, навіть при порівняно невеликих деформаціях призводить до виникнення великих пружних зусиль, впливають на конструкцію моста. Це викликає накопичення втоми металу і може привести до механічних поломок. Таким чином, гасіння поперечних коливань конструкції мостового крана є актуальним завданням, вирішення якої приділено мало уваги.
Вирішити це завдання можна, керуючи відповідним чином електроприводами коліс моста. Однак при цьому необхідно стежити, щоб гасіння коливань не супроводжувалося перекосом моста в поперечному напрямку, так як при цьому до коліс і приводних валів прикладаються значні за величиною згинальні моменти.
Розглядаючи пружні коливання мостового крана, необхідно представляти його конструкцію як систему з розподіленими параметрами. Однак створення математичного опису такої системи є досить складним завданням. До того ж з математичної моделі такої системи важко проводити синтез регуляторів. Тому при розгляді систем з розподіленими параметрами застосовують різні методи спрощення моделі об'єкта. У разі механічних об'єктів найбільш часто розподілені маси і пружності замінюють зосередженими, представляючи математичну модель об'єкта у вигляді багатомасової системи.
Точність отриманих таким чином лінійних математичних моделей залежить від того, наскільки адекватно виконаний перехід від моделі з розподіленими параметрами до моделі із зосередженими параметрами. Деякі автори [6, 8] розглядають міст як невагомий пружний зв'язок, рівномірно розподіляючи його масу між колесами і фіксуючи візок в одному з крайніх положень або нехтуючи її масою, що є дуже грубим допущенням.
В [2] розроблена лінійна математична модель мостового крана з візком, розташованим в середній частині мосту. При однакових масах коліс моста і пружність його частин праворуч і ліворуч від візка міст з візком представлений у вигляді двухмассовой системи, в якій колеса моста об'єднані в одну масу. Адекватність двухмассовой моделі оцінювалася шляхом порівняння її з віртуальною механічної моделлю в середовищі пакета Comsol, в якій розрахунок перехідних процесів виконується методом кінцевих елементів. В основу вибору параметрів цієї моделі було покладено рівність амплітуд коливань балки з двома закріпленими кінцями і вантажем, розташованим в її центрі збігається з амплітудою коливань вантажу, розташованого на невагомою балці, якщо до маси балки додати 17/35≈0.5 маси балки. Виявилось, що найбільше збіг амплітуд коливань зосереджених мас при заданій їх частоті в моделі з зосередженими параметрами та відповідних їх розташуванню точок металевої конструкції в моделі з розподіленими параметрами досягається при виконанні умови:

де mc1,3 — зосереджені маси першої та другої опор відповідно, які включають в себе масу коліс, електроприводів і кінцевих балок, mp — розподілена маса головних балок моста, mcT — зосереджена маса візка. Коефіцієнт жорсткості єдиною в цьому випадку пружного зв'язку можна легко розрахувати, знаючи частоту пружних коливань і зосереджені маси.
Значно складнішим є випадок, коли візок зміщений щодо центральної точки моста. При цьому пружності частин балок моста, ліворуч і праворуч від візка, будуть відрізнятися один від одного. Крім того, закон розподілу маси моста між його колесами і візком у функції положення візка не відомий. Проте, в [4] на підставі аналізу коливань мосту в точці розташування візки, виконаного в пакеті Comsol, обгрунтована можливість представлення моста з візком, встановленої в точці моста, відмінною від його центру, у вигляді трехмассовой системи, представленої на рис.1, та визначені параметри такої лінійної моделі для деяких фіксованих положень візки, з умови максимальної схожості перехідних процесів (частот і амплітуд пружних коливань).
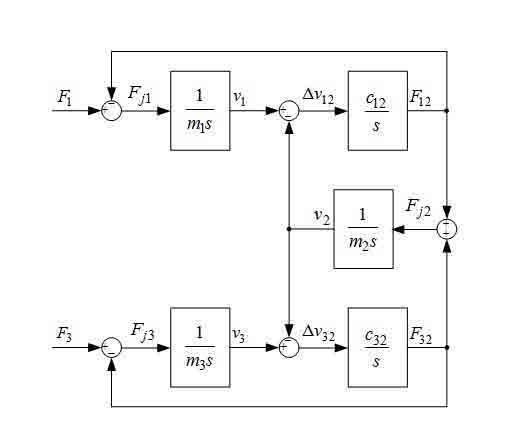
Рисунок 1 — Структурна схема трехмассовой системи
Метою роботи є синтез взаємозалежної двоканальної системи регулювання швидкістю коліс, здатної придушити поперечні коливання моста без його суттєвого перекосу, на основі запропонованої моделі.
1. Аналіз об'єкта регулювання
Насамперед, досліджуємо об'єкт регулювання. Модель рис.1 має характеристичний поліном:
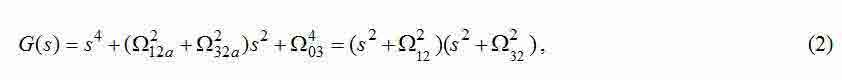
де
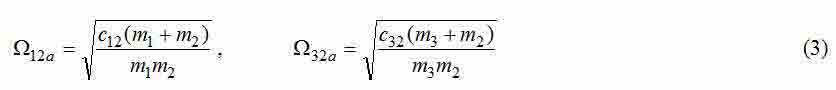
— частоти власних пружних коливань автономних двомасових систем 12 і 23;
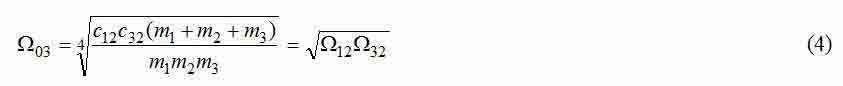
— середньогеометричнийі корінь характеристичного полінома розглянутої трехмассовой системи;
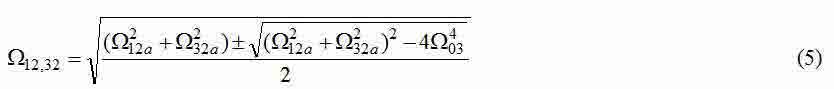
— частоти власних пружних коливань трехмассовой системи.
Передавальні функції (ПФ) від вхідних сил до динамічного зусилля, що впливає на другу масу, мають вигляд:
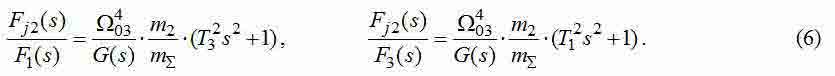
де

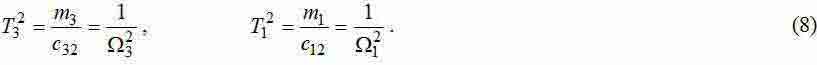
Розкладанням отриманих ПФ на суму дробів при рівності прикладених до коліс сил (F1+F2=F) отримаємо вирази для амплітуд кожної з гармонік:
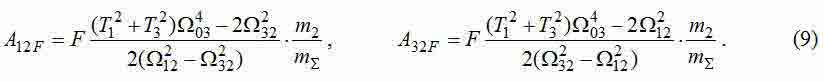
Отримані формули для частот і амплітуд коливань трехмассовой системи можуть бути використані для визначення параметрів моделі. Бажані чисельні значення частот і амплітуд можна отримати шляхом аналізу Фур'є результатів моделювання моста в пакеті Comsol. Враховуючи, що в цієї програмної середовищі зручно вимірювати швидкості переміщення різних точок моста, а не їх прискорення, то з амплітуд коливань пружного зусилля (8) необхідно визначити амплітуди коливань швидкості:
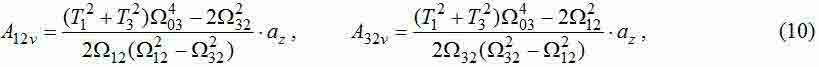
где  — завдання на прискорення моста.
— завдання на прискорення моста.
Прирівнюючи вирази (5) і (10) до відповідних значень, знайденим в результаті спектрального аналізу, і додаючи до отриманих таким способом 4 - м рівнянням рівняння (7), отримуємо систему 5 нелінійних рівнянь з 5-ма невідомими: [m1, m2, m3, c12, c32], яку можна вирішити чисельними методами.
Як вже зазначалося раніше, даний об'єкт регулювання (ОР) має змінні параметри. Розглянемо деякі окремі випадки, при яких зміна параметрів призводить до редукування ОР.
При розташуванні візка в центрі моста:
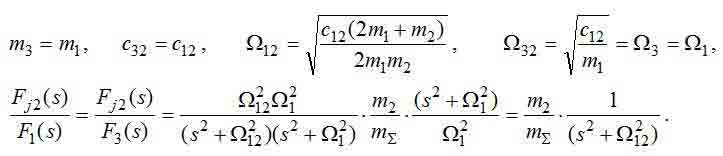
2. Аналіз типової двоканальної системи підпорядкованого регулювання швидкості
Маючи наближену лінійну модель об'єкта регулювання, можна приступити до синтезу системи автоматичного керування (САК).
У простому випадку для управління приводами коліс моста застосовують систему підлеглого регулювання швидкості (СПРШ), представлену на рис.2, без коригувальних зв'язків, позначених пунктирами. На цьому рисунку контури струмів (зусиль) двигунів представлені спрощено у вигляді аперіодичних ланок з малими постійними часу TT. Перехідні процеси, отримані при моделюванні такої системи для випадку розташування візки на відстані l=8 m від лівого краю моста, де умовно розташована зосереджена маса m1 при довжині мосту L=20 м показані на рис.3. Вони отримані при TT=4 mc і Tc1=Tc2=2TT. На цих графіках видно повільно затухаючі пружні коливання в сигналах сил і швидкостей, зменшити які можна шляхом зниження коефіцієнтів підсилення регуляторів швидкості та доповнення системи управління коригуючими зворотними зв'язками по різницям швидкостей Δv12 і Δv32 та, заведеними на входи регуляторів швидкості, як це показано на рис.4.
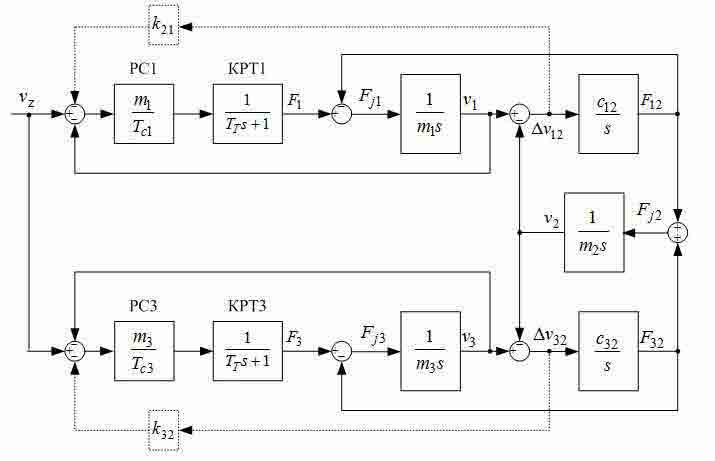
Рисунок 2 — Структурна схема системи підпорядкованого регулювання швидкості трехмассового об'єкта.
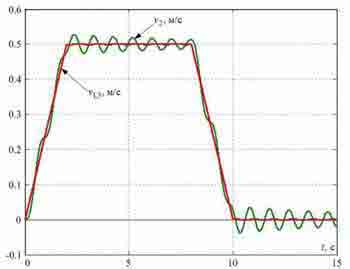
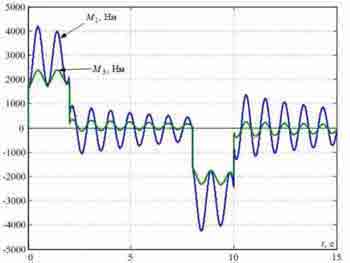
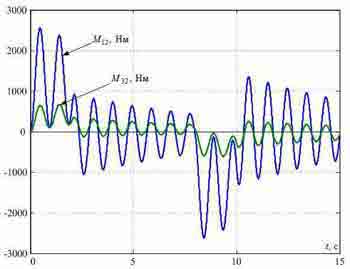
Рисунок 3 — Перехідні процеси в типовій СПРШ, синтезованої без урахування пружності металевих конструкцій.
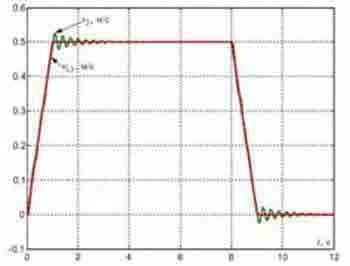
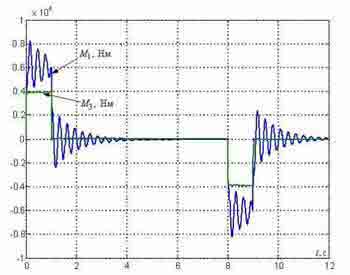
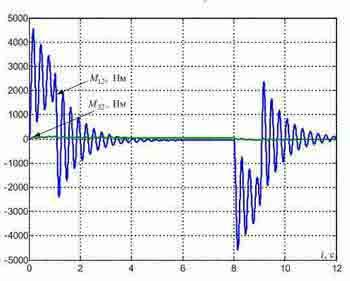
Рисунок 4 — Перехідні процеси в типовій СПРШ, синтезованої з урахуванням пружності металевих конструкцій.
3. Синтез і аналіз двоканальної системи підпорядкованого регулювання швидкості з додатковими зворотними зв'язками по різниці швидкостей зосереджених мас
Формули для розрахунку постійної часу інтегрування контуру швидкості та коригуючого коефіцієнта за різниці швидкостей першої та другої зосереджених мас виведені для системи управління двохмасовим об'єктом на підставі аналізу діаграм Вишнеградського [1] і з умов модульного оптимуму (МО) [2].
Використовуємо методику [2] для параметричного синтезу системи рис.2. Для цього необхідно знайти її передавальну функцію від завдання на швидкість до швидкості другого маси. Як показано в роботах [1, 2], при її виведенні можна знехтувати інерційністю швидкодіючого контуру струму. Така ПФ має вид:
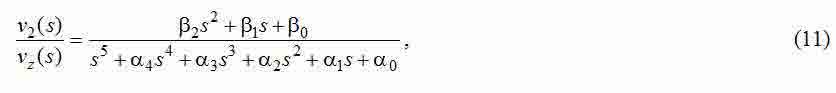
де

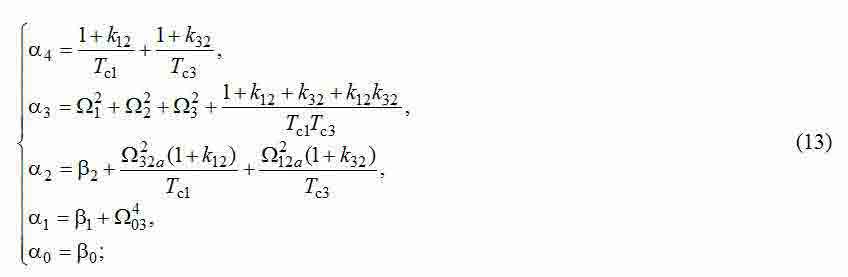
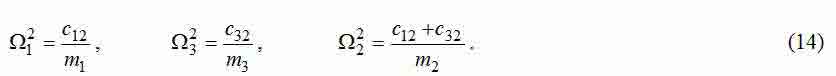
Для виведеної передавальної функції складаємо рівняння, що забезпечує досягнення МО [3, 4]. Щоб визначити як невідомі постійні часу Tc1, Tc3, так і коефіцієнти коригувальних зворотних зв'язків κ12, κ32, необхідно вирішити систему 4 -х рівнянь з 4 - ма невідомими:

Для синтезу СПРШ без додаткових коригувальних зв'язків необхідно у формулах (12), (13) покласти κ12=0, κ32=0 і для отриманих таким чином поліноміальних коефіцієнтів вирішити спільно два перших рівняння системи (15) відносно Tc1, Tc3. Результати моделювання показали, що, як і для двомасових систем, за відсутності коригуючих зворотних зв'язків по різницям швидкостей амплітуда і час загасання пружних коливань зменшуються недостатньо ефективно. Тому зупинимося на дослідженні СПРШ з додатковими зв'язками.
На жаль, аналітичне рішення рівнянь оптимізації для розглянутої системи отримати не вдалося, але чисельні рішення визначаються без особливих проблем. Починати процес параметричного синтезу слід з розміщення візки в центрі моста, коли трехмассова система вироджується в двомасову за рахунок того, що m1=m3 і c12=m32. Параметри САК в цьому випадку можна обчислити за формулами, узятим з [8] і кілька перетвореним з урахуванням особливостей двухмассовой моделі і необхідності подальшого переходу до представленої трехмассовой моделі:
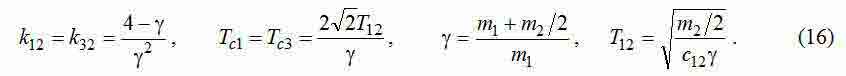
Параметри САК при розташуванні візка не в центрі моста слід визначати рішенням системи рівнянь (15) з коефіцієнтами (12), (13). Для забезпечення гарної збіжності ітераційного обчислювального процесу доцільно дискретно, з деяким кроком, переміщати візок від центру моста до одного з його коліс. В якості початкових наближень параметрів САК щоразу слід в якості початкових наближень параметрів використовувати їх значення, отримані на попередньому кроці.
Перехідні процеси в синтезованої СПРШ при Δl=2 м показані на рис. 5. Вони демонструють ефективність гасіння пружних коливань розглянутих точок моста запропонованим методом.
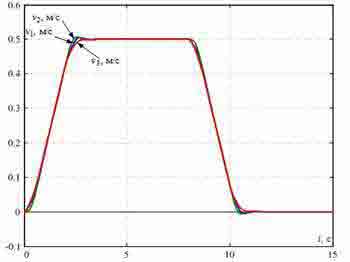
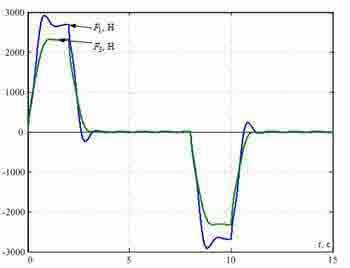
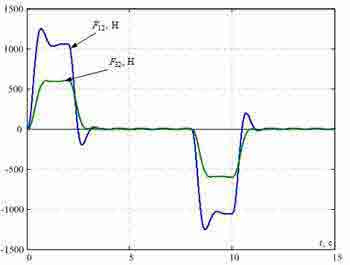
Рисунок 5 — Перехідні процеси в системі підпорядкованого регулювання, синтезованої з умов модульного оптимуму.
Для порівняння динамічних властивостей розробленої САК при різних положеннях візки на рис.6 наведені графіки зміни прискорення другої маси. З них видно, що при зміні Δl от 1м до 6 м швидкодія синтезованої системи підвищується, а характер зміни розглянутого сигналу залишається практично незмінним. Перерегулювання перехідної функції становить 10%. Поведінка прискорення другого маси при розташуванні візка в центрі моста випадає із загального ряду, тому що характеризується меншим перерегулюванням (8%) і більш високою швидкодією. Це пояснюється тим, що параметри САК в цьому випадку розраховувалися з інших рівнянь оптимізації, виведених для двухмассовой системи, передавальна функція якої має характеристичний поліном другого порядку і поліном впливу нульового порядку.
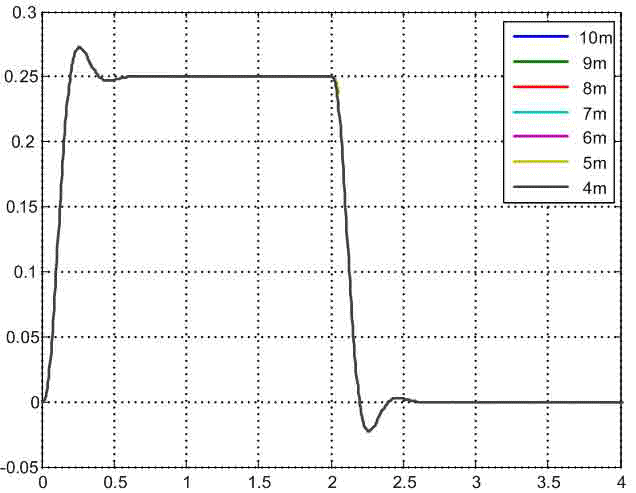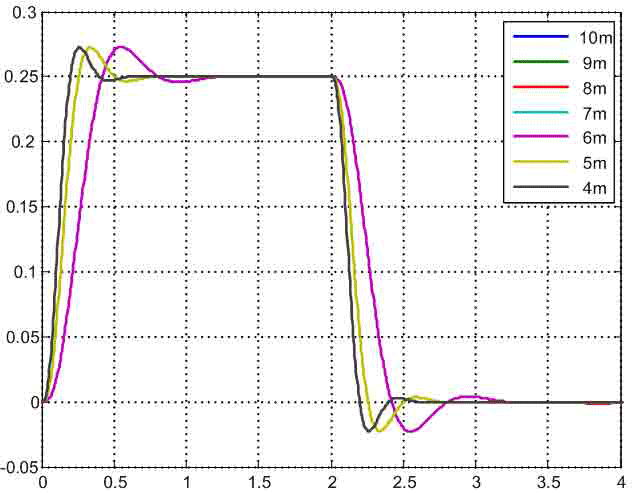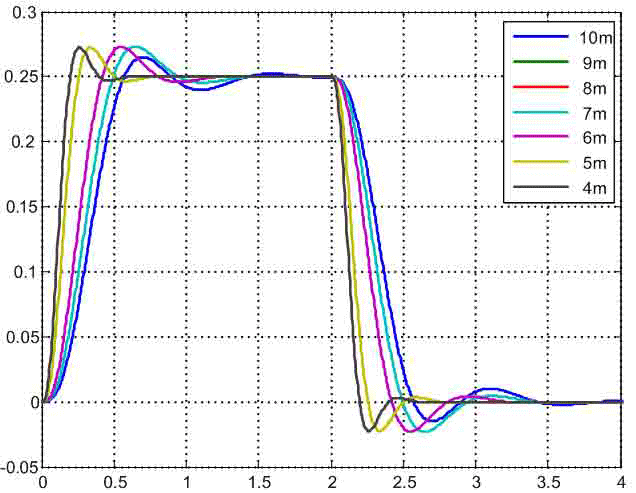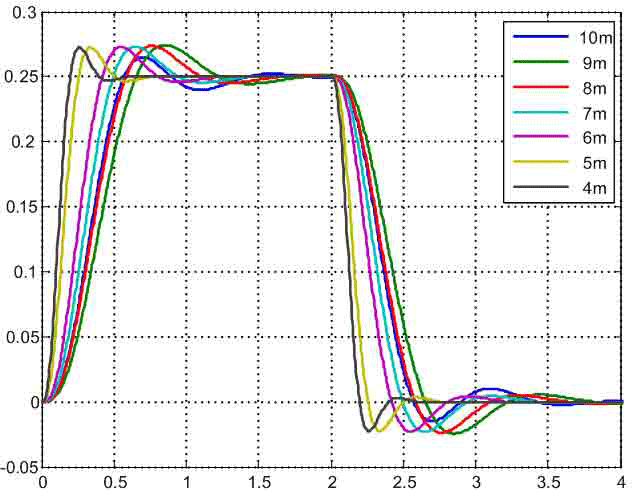
Рисунок 6 — Графіки зміни прискорення другої маси.
(анімація: 7 кадрів, 7 циклов повторення, 183 кілобайт)
Висновки
- СПРШ, синтезована без урахування пружних зв'язків демпфує коливання дуже слабо;
- СПРШ з додатковими коригувальними зв'язками по різниці швидкостей ефективно гасить пружні коливання, хоча і відрізняється дещо підвищеним перерегулюванням за сумарним пружному моменту і наявністю невеликого перерегулирования за швидкостями. Основною перевагою цієї системи є простота її реалізації, тому що всі сигнали зворотних зв'язків легко вимірюються;
- Запропоновані системи управління з постійними параметрами демпфують пружні коливання тільки при фіксованому положенні візка. Надалі необхідно розробити адаптивну САК, що здійснює подавлення коливань при русі візка по мосту.
Примітка. Під час написання цього реферату дипломна робота знаходиться ще на стадії виконання, тому наведений реферат містить наявні на момент складання іспиту з дисципліни «Інтернет-технології» інформацію. Кінцевий строк виконання магістерської роботи й дата захисту диплома – січень 2015 року.
Список літератури
- Борцов Ю.А., Соколовский Г.Г. Автоматизированный электропривод с упругими связями. – СПб.: Энергоатомиздат, 1992. – 288 с.
- Коцегуб П.Х., Баринберг В.А., Толочко О.И., Федоряк Р.В. Оптимизация двухмассовых систем регулирования скорости // Известия вузов. Электромеханика. – 1998. – №4. – С. 54-57.
- Kessler C. Uber die Vorausberechnung optimal abgestimmer Regelkreise // Regelungstechnik. 1955. – №1. – S. 16-22, №2. – S. 40-49.
- Коцегуб П.Х., Толочко О.И. Оптимизация систем управления по модулю амплитудно-частотной характеристики // Изв. вузов. Электромеханика. – 1977. – №6. – С. 679-684.
- Толочко О.І., Коцегуб П.Х., Федоряк Р.В. Дослідження впливу середньогеометрічного кореня характеристичного полінома на властивості системи модального керування двомасовим електромеханічним об‘єктом // Наукові праці ДонДТУ. Серія „Електротехніка і енергетика”. – Донецьк: ДонДТУ. – 2002. – №41. – С. 146-155.
- Бургин Б.Ш. Анализ и синтез двухмассовых электромеханических систем. – Новосибирск: Новосиб. электротехн. ин-т, 1992. – 199 с.
- Александров Е.Е., Кузнецов Б.И., Радиевский А.Е., Тернюк Н.Э. Оптимизация электромеханических систем с упругими связями. – Харьков: IMIC, 1995. – 304 с.
- Тарарыкин С.В., Тютиков В.В. Проектирование регуляторов состояния упругих электромеханических систем // Электричество. – 1998. – №3. – С. 52-57.
- Герасимяк Р.П., Ант А.М., Рамарувахуака А.М. Синтез электромеханической системы подъемных механизмов с подавлением упругих колебаний // Електромашинобудування та електрообладнання. – 1996. – № 48.
- Герасимяк Р.П., Рамарувахуака А.М. Система управления электропривода двухмассовой электромеханической системой // Электротехника. – 1998. – №6. – С. 28-31.
- Коцегуб П.Х., Толочко О.И., Федоряк Р.В. Практическая реализация цифровых САУ в среде пакета Матлаб с использованием платформы реального времени „QNX TARGET” // Вісник Національного технічного університету „ХПІ”. – Харків: НТУ ХПІ. – 2002. – Т.1, №12.– С. 98-101.
- Real-TimeWorkshop. For Use with Simulink. User’s Guide. The MathWorks Inc., 2000. – 622 p.
