Abstract
Contents
- Introduction
- 1. Analysis of object regulation
- 2. The analysis of standard two-channel system of the subordinated speed regulation
- 3. Synthesis and the analysis of two-channel system of the subordinated speed regulation with additional feedback on a speeds difference of the concentrated masses
- Conclusion
- References
Introduction
The bridge cranes representing set of three main mechanisms are widely applied to movement of freights in industrial conditions:
- the bridge moving on rails, laid on subcrane beams along flight of the opened or closed cargo platform;
- carts with the freight suspended to it, moving along the bridge, i.e. across platform flight;
- the lifting device in the form of the winch for winding a rope to which transported freight is attached.
The bridge span for the majority of cranes makes from 10,5 m to 34,5 m (with a step of 3 m). Therefore at bridge and cart movement the main beams of the bridge having big length at rather small cross section, make elastic fluctuations diversely, causing the increased wear of a metalwork and mechanisms.
A large number of works [2, 3, 5]. is devoted to a problem of research vertical fluctuations of a design the bridge crane. Really, fluctuations in this direction have the biggest amplitude and negatively wag not only on the bridge, but also and on a rope which taking into account its own elasticity, gradually loses the durability. Nevertheless, elasticity of a design in the horizontal direction, being shown mainly when moving bridge, even at rather small deformations leads to emergence of the big elastic efforts influencing a design of the bridge. It causes accumulation of fatigue metal and can lead to mechanical breakages. Thus, clearing of cross fluctuations a design of the bridge crane is the actual task to which decision not enough attention is paid.
It is possible to solve this problem, operating as appropriate electric drives of bridge wheels. However thus it is necessary to watch that clearing of fluctuations wasn't accompanied by a bridge distortion in the cross direction as thus the bending moments are put to wheels and power shafts considerable in size.
Considering elastic fluctuations of the bridge crane, it is necessary to represent its design as system with the distributed parameters. However creation of the mathematical description of such system is quite complex challenge. Besides on mathematical model of such system it is difficult to carry out synthesis of regulators. Therefore by consideration of systems with the distributed parameters apply various methods of simplification model object. In case of mechanical objects most often distributed masses and elasticity replaces concentrated, representing mathematical model object in the form of multimass system.
Accuracy of the linear mathematical models received thus depends on that, transition from model with the distributed parameters to model with the concentrated parameters is how adequately executed. Some authors [6, 8] consider the bridge as weightless elastic communication, evenly distributing its weight between wheels and fixing the cart in one of extreme provisions or neglecting it the weight that is very rough assumption.
In [2] the linear mathematical model of the bridge crane with the cart located in a middle part of the bridge is developed. With an identical mass of bridge wheels and the elastics of his parts on the right and to the left of the cart the bridge with the cart is presented in the form of two-mass system in which wheels of the bridge are united in one weight. Adequacy of two-mass model was estimated by its comparison with virtual mechanical model in the environment of a Comsol package in which calculation of transients is carried out by a method of final elements. Equality of amplitudes fluctuations, a beam was the basis for a choice parameters of this model with two fixed ends and the freight located in its center coincides with amplitude fluctuations of the freight located on a weightless beam if to mass of a beam to add 17/35≈0.5 mass of a beam. It appeared that the greatest coincidence of amplitudes fluctuations of the concentrated masses with a set their frequency in model with the concentrated parameters and the points of a metal design corresponding to their arrangement in model with the distributed parameters is reached when performing condition:

where mc1,3 — the concentrated mass of the first and second support respectively which include the wheels mass, electric drives and trailer beams, mp — the distributed mass of the main beams bridge, mcT — the concentrated mass of the cart. The coefficient of rigidity the only in this case elastic communication can be calculated easily, knowing the frequency of elastic fluctuations and the concentrated masses.
The case when the cart is displaced rather central point of the bridge is much more difficult. Thus elasticity parts of beams of the bridge, at the left and to the right of the cart, will differ from each other. Besides, the law distribution mass of the bridge between its wheels and the cart as position of the cart isn't known. Nevertheless, in [4] on the basis analysis of bridge fluctuations in a point an arrangement of the cart, made in a Comsol package, possibility of representation bridge with the cart installed in a point of the bridge, other than its center, in the form of the three-mass system presented in fig. 1 is proved, and parameters such linear model for some fixed provisions of the cart, from a condition of the maximum similarity transients (frequencies and amplitudes of elastic fluctuations) are determined.
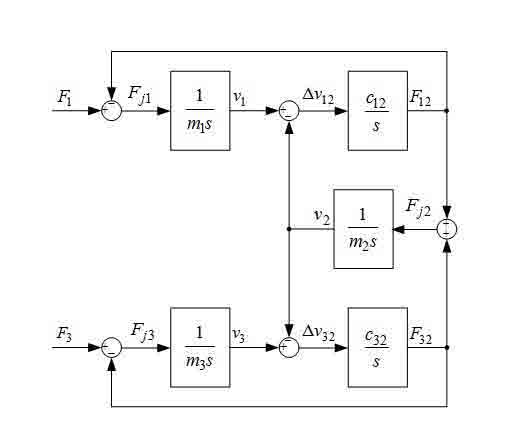
Fig. 1 — Block diagram of three-mass system
The purpose of work is synthesis of the interconnected two-channel system regulation by the speed of the wheels, capable to suppress cross fluctuations bridge without its essential distortion, on the basis of the offered model.
1. Analysis of object regulation
First of all, we investigate object of regulation. The model of fig. 1 has a characteristic polynom:
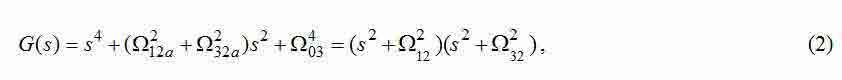
where
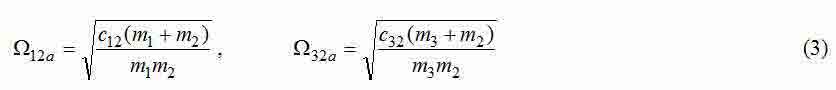
— frequencies of own elastic fluctuations autonomous two-mass systems 12 and 23;
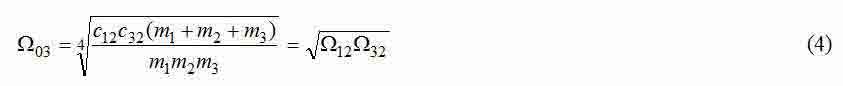
— compound root of a characteristic polynom considered three-mass system;
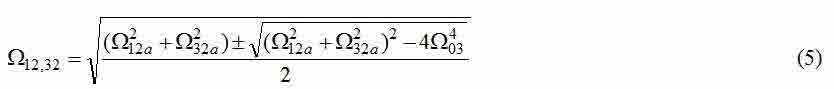
— frequencies of own elastic fluctuations of three-mass system.
The Transfer Functions (TF) from entrance forces to the dynamic effort influencing the second weight, have an appearance:
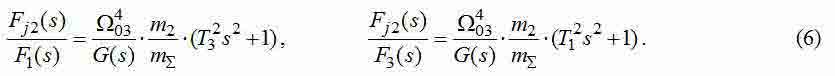
where

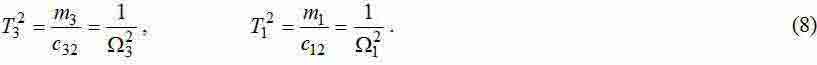
Decomposition received TF for the sum of fractions at equality of forces applied to wheels (F1+F2=F) we will receive expressions for amplitudes of each of harmonicas:
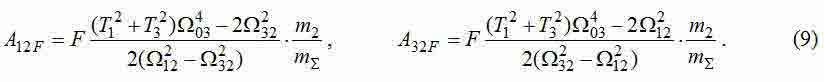
The received formulas for frequencies and amplitudes fluctuations of three-mass system can be used for determination of parameters model. Desirable numerical values of frequencies and amplitudes can be received by bridge Fourier's analysis of results modeling in a Comsol package. Considering that it is convenient to measure speeds of movement in different points of the bridge, instead of their acceleration in this program environment, from amplitudes fluctuations of elastic effort (8) it is necessary to determine amplitudes fluctuations of speed:
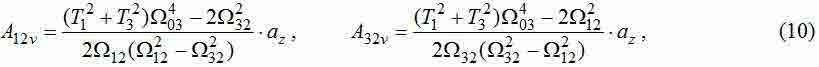
where  — task for bridge acceleration.
— task for bridge acceleration.
Equating expressions (5) and (10) to the corresponding values found in result of the spectral analysis, and adding to the 4th equations received in such a way the equation (7), we receive system of 5 nonlinear equations with 5 unknown: [m1, m2, m3, c12, c32], which can be solved numerical methods.
As it was already noted earlier, the considered object of regulation (OR) has variable parameters. We will consider some special cases at which change parameters leads the SHOUTING to reduction.
At a cart arrangement in the bridge center:
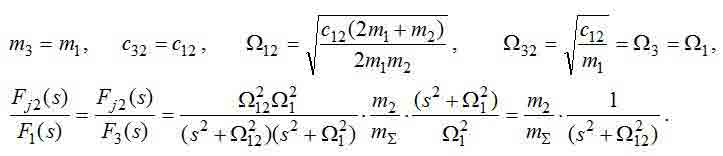
2. The analysis of standard two-channel system of the subordinated speed regulation
Having approximate linear model of object regulation, it is possible to start synthesis system of automatic control (SAC).
In the elementary case to control of wheels drives of the bridge apply the system subordinated regulation of speed (SSRS) presented in fig. 2, without the correcting communications designated by dotted lines. In this drawing contours of currents (efforts) engines are presented simply in the form of aperiodic links with small constants time of TT. The transients received at modeling of such system for a case of an arrangement cart at distance of l=8 m from the left edge of the bridge where the concentrated weight m1 m1 is conditionally located, with a length of the bridge L=20 m are shown in fig. 2. They are received at TT=4 mc and Tc1=Tc2=2TT. On these schedules slowly fading elastic fluctuations in signals of forces and speeds are visible, to reduce which it is possible by decrease in coefficients strengthening of speed regulators and addition of a control system with correcting feedback on differences of speeds Δv12 and Δv32, got on entrances of speed regulators as it is shown in fig. 3.
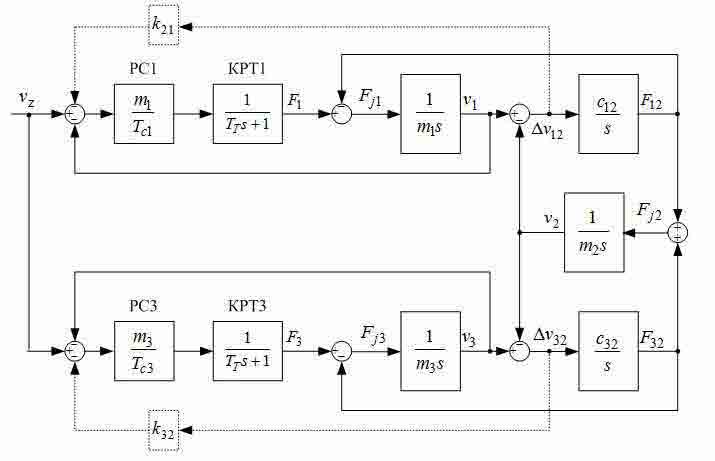
Fig. 2 — Block diagram of system of the subordinated speed regulation three-mass object
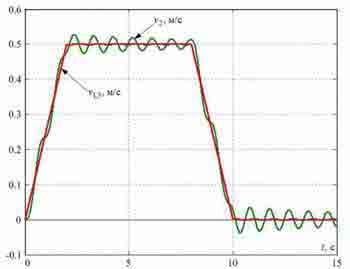
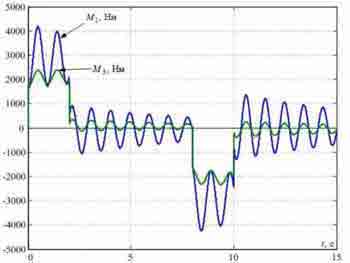
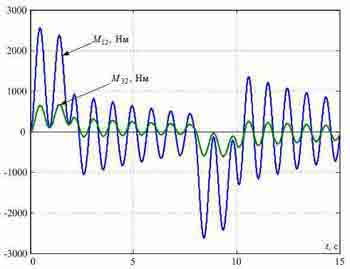
Fig. 3 — Transients in the standard SPRS synthesized without elasticity of metal designs
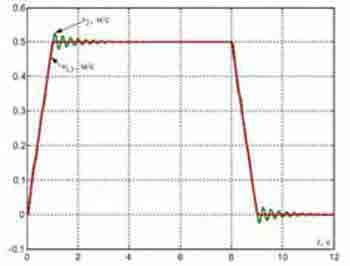
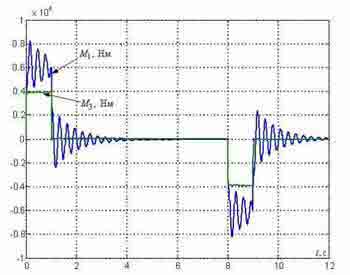
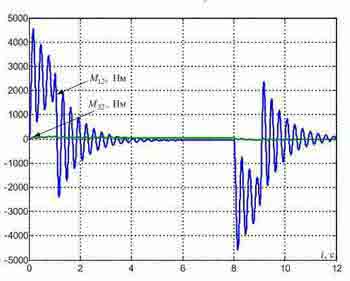
Fig. 4 — Transients in the standard SPRS synthesized with the accounting of elasticity of metal designs
3. Synthesis and the analysis of two-channel system of the subordinated speed regulation with additional feedback on a speeds difference of the concentrated masses
Formulas for calculation of a constant time of integration a contour speed and the correcting coefficient on a difference of speeds the first and second concentrated masses are brought for a control system of two-mass object on the basis analysis of charts Vyshnegradsky [1] and out of conditions of the modular optimum (MO) [2].
We use a technique [2] for parametrical synthesis of system fig. 2. For this purpose it is necessary to find its transfer function from a task speed to the speed of the second weight. As shown in works [1, 2], at its conclusion it is possible to neglect a lag effect of a high-speed current contour. Such TF has an appearance:
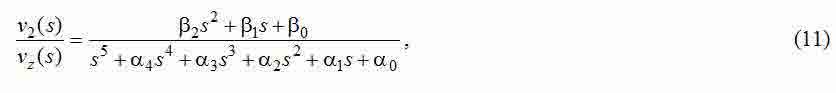
where

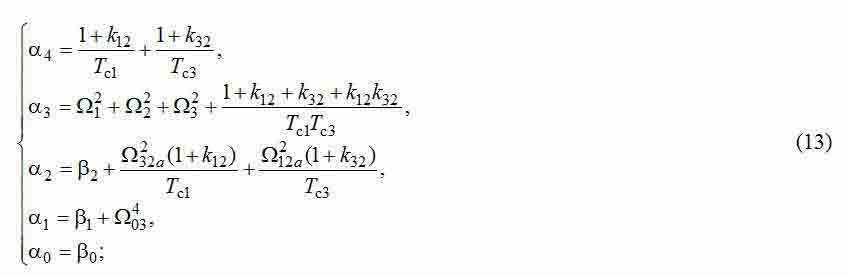
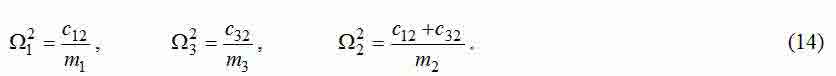
For the removed transfer function we work out the equations, providing achievement of MO [3, 4]. To define as unknown constants time Tc1, Tc3, and coefficients of correcting feedback κ12, κ32, it is necessary to solve system of 4 equations with 4 unknown:

For SPRS synthesis without additional correcting communications it is necessary to put in formulas (12), (13), κ12=0, κ32=0 and for the polynomial coefficients received thus to solve in common the two first the equations of system (15) relatively Tc1, Tc3. Results of modeling showed that, as well as for two-mass systems, in the absence of correcting feedback on differences speeds amplitude and time attenuation of elastic fluctuations decrease not rather effectively. Therefore we will stop on research SPRS with additional communications.
Unfortunately, the analytical solution of the equations optimization for considered system didn't manage to be received, but numerical decisions are defined without special problems. It is necessary to begin process of parametrical synthesis with cart placement in the bridge center when the three-mass system degenerates in two-mass because and. The SAC parameters in this case can be calculated on the formulas taken from m1=m3 и c12=m32 two-mass model a little transformed taking into account features and need of the subsequent transition to presented three-mass model:
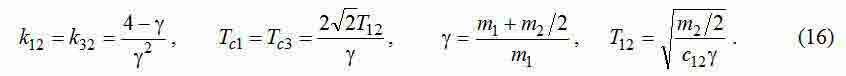
The SAC parameters at a cart arrangement not in the center of the bridge should be determined by the decision of system equations (15) with coefficients (12), (13). For ensuring good convergence of iterative computing process expediently discretely, with some step to move the cart from the bridge center to one of its wheels.
Transients in synthesized SPRS at Δl=2 are shown in fig. 5. They show efficiency clearing of elastic fluctuations in considered points of the bridge the offered method.
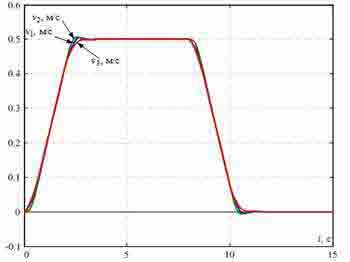
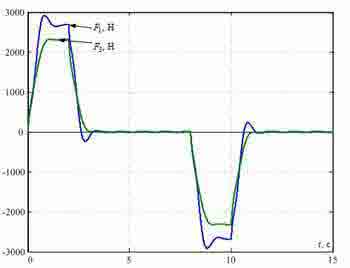
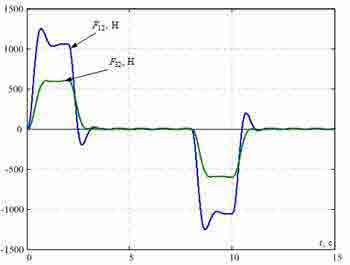
Fig. 5 — Transients in the system of the subordinated regulation synthesized from conditions of a modular optimum
For comparison dynamic properties of developed SAC at different provisions of the cart schedules change acceleration of the second weight are given in fig. 6. From them it is visible that at change Δfrom 1 m to 6 m speed of the synthesized system increases, and nature of change a considered signal remains almost invariable. Reregulation of transitional function makes 10%. The behavior of acceleration of the second weight at a cart arrangement in the center of the bridge drops out of a general series since it is characterized by smaller reregulation (8%) and higher speed. This results from the fact that the SAC parameters in this case paid off from other equations of optimization removed for two-mass system which transfer function has a characteristic polynom of the second order and a polynom influence of a zero order.
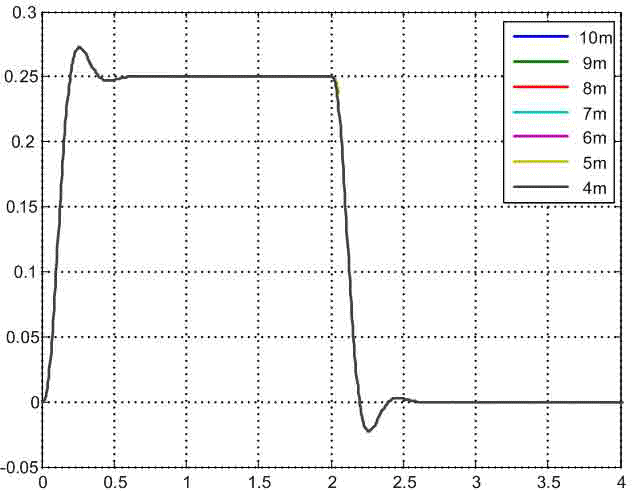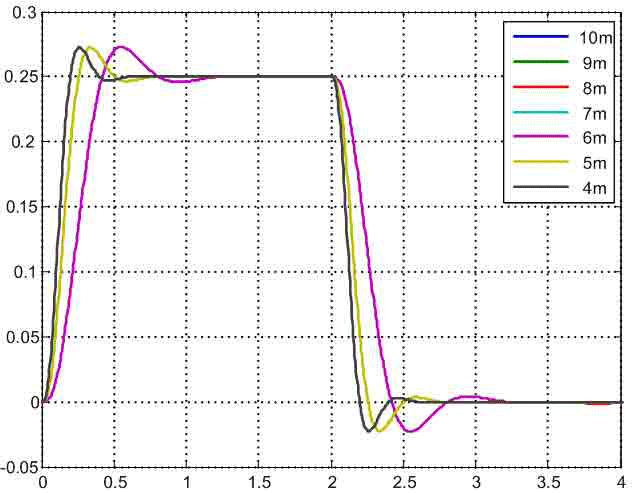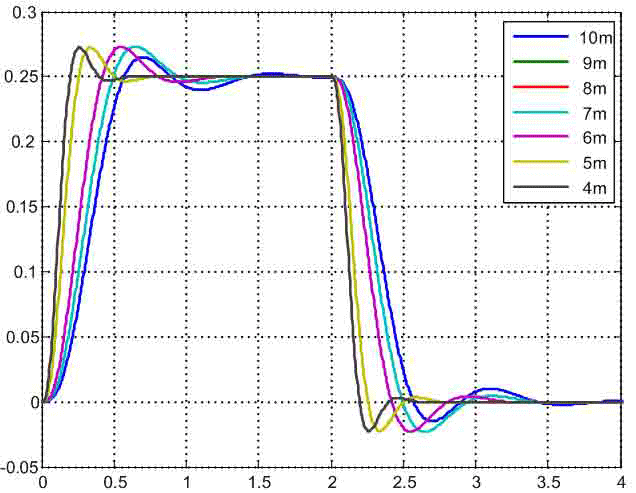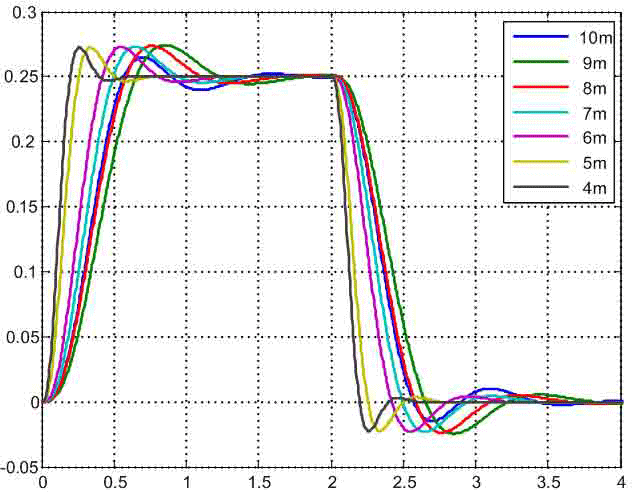
Fig. 6 — Schedules of acceleration change in the second weight
(animation: 7 frames, 7 cycles, 183 kilobytes)
Conclusion
- SPRS synthesized without elastic communications damps fluctuations very poorly;
- SPRS with additional correcting communications on a difference of speeds effectively extinguishes elastic fluctuations, though differs a little increased reregulation on the total elastic moment and existence of small reregulation on speeds. The main advantage of this system is simplicity of its realization since all signals of feedback are easily measured;
- The offered control systems with constant parameters damp elastic fluctuations only at the fixed position of the cart. Further it is necessary to develop the adaptive SAC which is carrying out suppression of fluctuations at movement of the cart on the bridge.
Note. When writing this text the work was still in progress, so the essay contains results available at the time of the exam on the subject Internet-technology
. The deadline for master’s thesis and date of defense – January 2015.
References
- Борцов Ю.А., Соколовский Г.Г. Автоматизированный электропривод с упругими связями. – СПб.: Энергоатомиздат, 1992. – 288 с.
- Коцегуб П.Х., Баринберг В.А., Толочко О.И., Федоряк Р.В. Оптимизация двухмассовых систем регулирования скорости // Известия вузов. Электромеханика. – 1998. – №4. – С. 54-57.
- Kessler C. Uber die Vorausberechnung optimal abgestimmer Regelkreise // Regelungstechnik. 1955. – №1. – S. 16-22, №2. – S. 40-49.
- Коцегуб П.Х., Толочко О.И. Оптимизация систем управления по модулю амплитудно-частотной характеристики // Изв. вузов. Электромеханика. – 1977. – №6. – С. 679-684.
- Толочко О.І., Коцегуб П.Х., Федоряк Р.В. Дослідження впливу середньогеометрічного кореня характеристичного полінома на властивості системи модального керування двомасовим електромеханічним об‘єктом // Наукові праці ДонДТУ. Серія „Електротехніка і енергетика”. – Донецьк: ДонДТУ. – 2002. – №41. – С. 146-155.
- Бургин Б.Ш. Анализ и синтез двухмассовых электромеханических систем. – Новосибирск: Новосиб. электротехн. ин-т, 1992. – 199 с.
- Александров Е.Е., Кузнецов Б.И., Радиевский А.Е., Тернюк Н.Э. Оптимизация электромеханических систем с упругими связями. – Харьков: IMIC, 1995. – 304 с.
- Тарарыкин С.В., Тютиков В.В. Проектирование регуляторов состояния упругих электромеханических систем // Электричество. – 1998. – №3. – С. 52-57.
- Герасимяк Р.П., Ант А.М., Рамарувахуака А.М. Синтез электромеханической системы подъемных механизмов с подавлением упругих колебаний // Електромашинобудування та електрообладнання. – 1996. – № 48.
- Герасимяк Р.П., Рамарувахуака А.М. Система управления электропривода двухмассовой электромеханической системой // Электротехника. – 1998. – №6. – С. 28-31.
- Коцегуб П.Х., Толочко О.И., Федоряк Р.В. Практическая реализация цифровых САУ в среде пакета Матлаб с использованием платформы реального времени „QNX TARGET” // Вісник Національного технічного університету „ХПІ”. – Харків: НТУ ХПІ. – 2002. – Т.1, №12.– С. 98-101.
- Real-TimeWorkshop. For Use with Simulink. User’s Guide. The MathWorks Inc., 2000. – 622 p.
