Українська  English
ДонНТУ   Портал магистров

Реферат по теме выпускной работы

Содержание

Введение

В экосистеме обитает огромное количество организмов. Значительная часть из этих организмов – микроорганизмы, которые при попадании в организм человека вызывают негативное влияние. Проникновение одной формы живых существ, преимущественно микроорганизмов, в более высокоорганизованные организмы обозначают термином «инфекция»[1].

Инфекционные болезни являются одной из важных проблем современной медицины и остаются наиболее опасными и распространенными. Единственную инфекционную болезнь, которую удалось практически ликвидировать – ветряная оспа. В то время, как в мире насчитывается сотни инфекций, с которыми не известен способ борьбы. Самими распространенными инфекциями являются: холера, бубонная чума, грипп, брюшной тиф, оспа.

За свою жизнь человек неоднократно подвергается заболеваниям. Чаще всего за год человек болеет на вирусные инфекционные заболевания и это является причиной его временной нетрудоспособности. Наибольшую группу риска составляют дети и личности репродуктивного возраста. От инфекционных болезней ежегодно умирает более 16 млн. человек, то есть столько же, сколько суммарно от заболеваний сердечно-сосудистых и злокачественных образований [1].

1. Актуальность темы

Современная медицина для своей практики и теории применяет математические, физические и технические методы, что дает возможность не только поставить диагноз, но и установить причину болезни.

Развитие и внедрение в медицинскую практику разнообразных методов исследований в настоящее время все чаще приводят к необходимости применения математических методов [4]. Поэтому на сегодняшний день актуальными является следующие проблемы:

Таким образом, актуальность темы моделирования протекания вирусного заболевания заключается в необходимости делать прогноз во времени для каждого пациента с учетом его возрастной категории, времени распространения вируса в организме и объема поврежденных тканей для эффективного лечения.

2. Цель и задачи исследования

Целью исследования является разработка модели процесса протекания вирусного заболевания, которая позволила бы учесть индивидуальные характеристики пациента и тяжесть заболевания, и на основании чего выбрать эффективное лечение.

Для достижения цели работы необходимо выполнить следующие задачи:

  1. Рассмотреть особенности процесса протекания вирусного заболевания.
  2. Выполнить обзор существующих моделей прогноза динамики протекания и распространения вирусного инфекционного заболевания.
  3. Разработать динамическую модель протекания вирусного заболевания, с целью выбора эффективного лечение.

Объект исследования: вирусное заболевание, его динамика и лечение.

Предмет исследования: существующие модели прогноза динамики течения вирусного заболевания и методы лечения.

3. Обзор существующих моделей прогноза вирусных заболеваний

Существует два основных направления распространения вирусного заболевания. К первому направлению следует отнести распространения эпидемии, а второе направление – поражение инфекцией конкретного человека. Первое направление имеет большое социально-экономическое значение для общества и государства. Данный тип моделирования используется для прогноза и моделирования эпидемии в динамики. Второе же направление делает акцент на моделирование динамики протекания инфекционного заболевания для конкретного индивида с учетом особенностей его организма. Данное моделирование предназначено для прогноза и эффективного лечение пациента.

3.1 Обзор международных источников

Для получения оперативной информации о состоянии зараженного организма и с целью прогнозирования дальнейшего распространения инфекции применяют методы математического моделирования. Большая часть моделей распространения заболеваний основана на использовании алгебро-дифференциальных уравнения. Наиболее известной среди таких является модель SIR, предложенная В.А. Керманом и А.Г. Мак-Кендриком. В этой модели, как и в других моделях такого типа, вся популяция моделируемой территории делится на группы: «Susceptible» – здоровые люди, восприимчивые к заболеванию (обозначают их количество S), «Infectious» – инфекционные больные (обозначают их количество I), «Recovered» – переболели моделируемым заболеванием люди, более к нему не восприимчивы (обозначают их количество R) [17].

Грегори Л. Армстронг и Бет П. Белл в работе "Вирусный гепатит A в США: оценки и последствия для иммунизации детей на основе модели" преставали результаты, которые позволяют  существенно снизить заболеваемость гепатитом в целом [18].

3.2 Обзор национальных источников

В Харьковском национальном университете радиоэлектроники (ХНУРЭ) на кафедре биомедицинской инженерии (БМИ) занимаются научной деятельностью по следующим направлениям: исследования в областях микропроцессорных и микроконтроллерных систем, обработка медицинских изображений и сигналов, разработка программно-аппаратного обеспечения нейрохирургических систем, исследование информационных технологий в медицине, математическое моделирование и приборостроение в медицине, создание биомедицинских систем, оптимизация создания цифроаналоговых устройств, исследование электрохемилюминесценции и нанофотоники, формирование и анализ акустических полей природного и техногенного происхождения [11].

В Донецком национальном университете функционирует кафедра инфекционных болезней. Сотрудники кафедры занимаются лечением больных в клинике, консультативной работой в отделениях больницы, Гепатологическом Центре, осуществляют выезды по линии экстренной медицинской помощи в города и районы области. На базе кафедры создано и функционирует Донецкое областное научно-медицинское общество инфекционистов. Основной целью деятельности Общества является повышение уровня научно-медицинской подготовки практических врачей Донецкой области. Основными направлениями научной деятельности кафедры являются вирусные гепатиты, инфекции центральной нервной системы и TORCH-инфекции. При кафедре был организован первый в Украине Центр Консультативной и Лечебно-диагностической Помощи Больным Вирусными Гепатитами [16].

С целью краткосрочного прогнозирования заболеваемости эпидемическим паротитом и ветряной оспой В.Д. Денисенко (1982) использовал математический аппарат автокорреляции, описывающий характер многолетних и внутригодовых колебаний эпидемического процесса. Прогнозирование проводилось на основе данных ежемесячной заболеваемости в 9 крупных городах Украины за 10-11 лет. Эта модель по сравнению с рассмотренными выше, реализует формальный подход к прогнозированию эпидемического процесса и поэтому в меньшей степени отвечает предъявляемым в таких случаях требованиям [3].

Модель С.Г. Кривенкова и Ю.П. Рыкушина для паротита основана на системе дифференциальных уравнений с отклоняющимся аргументом (ДУОА) [3]. Для моделирования эпидемиологического процесса используют несколько классов моделирования: формальную аппроксимацию (приближение), формальную экстраполяцию (в основном кривых заболеваемости) и содержательное моделирование эпидемического процесса с дискретным или непрерывным течением [3]. Моделирование протекания вирусного заболевания в организме человека с помощью системы нелинейных обыкновенных дифференциальных уравнений представлено в источнике [4].

3.3 Обзор локальных источников

В Донецком национальном техническом университете научные работы, которые бы касались вопросов моделирование динамики протекания протекания вирусного заболевания отсутствуют. Но есть научные труды на схожие тематики:

1. "Варианты классификации по байесу для прогноза развития пневмонии при острых отравлениях психотропными средства" авторы: Ельков А.Н., Ильяшенко К.К. [12].

2. "Построение запросов к базе медицинских рентгеновских снимков на основе анализа векторного представления изображений" авторы: Бовырин А.В., Губанов А.В., Колесов А.И., Курякин В.Ф., Родюшкин К.В., Чудинович Б.М.[13].

3. "Pазработка специализированной компьютерной системы обработки томограмм для диагностики заболевания поджелудочной железы" автор Дейнега М.Ф.[14].

4. "Лікувльне та профілактичне плавання при захворюваннях сколіозом" авторы: Семенова Н.Л., Cухарева Л.В., Стойка Р.В.[15].

4. Решение задач и результаты исследований.

Система нелинейных обыкновенных дифференциальных уравнений, которая описывает динамику вирусного заболевания [4], представлена в выражении (1):

где βVdt – прирост числа вирусов dV за интервал времени dt;

γFVdt – описывает число вирусов, которые нейтрализуются антителами F;

τ – время, в течении которого осуществляется формирование каскада плазменных клеток;

α – коэффициент, учитывающий вероятность, с которой один антиген способен возбудить реакцию организма;

p – константа;

C – иммунологический уровень плазменных клеток в организме;

ρCdt – генерация антител плазменными клетками;

ηγVF – учитывает уменьшение числа антител в интервале времени за счет связи с антигенами и выходом из дальнейшей активной борьбы;

μf – коэффициент, обратно пропорциональный времени распада антитела;

dm – описывает изменение пораженной ткани;

σVdt – ткань организма, которая была разрушена вирусами;

μmmdt – ткань восстановленная за счет деятельности организма.

Основными действующими фактурами вирусного заболевания является: количество вирусов в организме V, число плазменных клеток C, производящих антитела F, и масса поврежденных вирусами ткани M. Первое уравнение системы (1) описывает изменение числа вирусов в организме. Второе уравнение системы (1) определяет рост плазменных клеток C. Третье уравнение системы (1) позволяет подсчитать баланс числа антител данной структуры, реагирующих с антителами вируса. Последнее уравнение из модели характеризует баланс поврежденной ткани организма при данном заболевании [4].

Пусть имеются математическая модель прогноза изменения состояния пациента в результате применения медикаментозной терапии:

                                                zi=fi(u1,...,un;αi), i=1,...,m,                                                                                                                                                              (2)

где αi  – нечёткие параметры, характеризующие степень тяжести заболевания.

Ограничения, наложенные на составляющие векторов u  и z, которые определяют их допустимые области измерения, представим в следующем виде:

    gj(u,z)≥0, j=1,...,J.                                                                                                                                                                         (3)

Частные целевые функции fi(u1,...,un;αi), i=1,...,m составляют векторную функцию f и различаются своими коэффициентами относительной важности (весами) (γ1,...,γm), значения которых могут изменяться.

Требуется найти вектор управления u*=(u1,...,u*n), обеспечивающий наилучшее приближение к желаемым значениям локальных критериев f*i:

                                     

где fi(u,αi) – нечёткие локальные критерии, значения которых вычисляются по моделям; 

f*i – желательные (идеальные) значения локальных критериев, задаваемых ЛПР;

gj(u) – ограничения на составляющие вектора u;

bj – заданные числа;

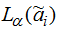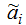 эль альфа от альфа итого с волной – множество уровня α нечётких параметров альфа итое с волной, введённое для учёта нечёткости параметров αi.

В качестве вектора управляющих параметров u= (u1,...,un) выступает набор дозировок n препаратов назначаемой базисной и ингаляционной терапии.

Нечёткие параметры αi  зададим в виде лингвистической переменной, которая будет характеризовать тяжесть заболевания. Допустим, лингвистическая  переменная αi  будет состоять из трёх термов, что будут характеризовать лёгкую, среднюю и тяжёлую форму протекания заболевания.

Эффективность лечения, как правило, оценивается по следующим критериям [7]: выраженность основных симптомов (f1), улучшение состояния пациента при анализе катамнеза (f2, иммуномодулирующий эффект проводимой терапии (f3), которые составляют векторную функцию f и различаются весами. Значения функции f1 определяется в результате осмотра врача, f3 – с помощью анализа иммунограммы. А функцию  f2 предлагается спрогнозировать с учетом формы тяжести заболеваний.

Для решения подобных задач целесообразно использовать подход, основанный на принципе гарантированного результата [8]. В этом случае производится минимизация наибольшего отклонения нечётких значений локальных критериев от их эталонных значений при выполнении наложенных ограничений:

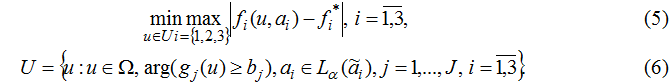
                                          система (5-6)

При нечётких ограничениях в задаче (5)-(6) необходимо построить функцию принадлежности μj(u), j=1,J выполнения каждого из ограничений g j≥bj, j=1,J.

Целесообразность минимаксной постановки задачи принятия решений можно объяснить тем, что назначенная терапия должна обеспечивать гарантированный результат выздоровления пациента.

Данную задачу многокритериальной оптимизации в условиях неопределённости можно свести к задаче многокритериальной оптимизации на основе множеств уровня α , что позволит осуществить поиск рациональных вариантов решения по выбираемым критериям [8].

Предлагается использовать следующий алгоритм решения задачи:

1. Выделить диапазоны значений  α для различных степеней тяжести протекания заболевания. Например, могут быть выделены следующие степени тяжести (СТ) заболевания:

СТ=1, при  0,7≤α≤1,0 - тяжёлая форма;

СТ=2, при 0,3≤α≤0,7 - средняя форма;

СТ=3, при 0,0≤α≤0,3 - лёгкая форма.

2. ЛПР должен назначить желательные (эталонные) значения локальных критериев f*i.

3. Рассчитать минимаксные (гарантированные) варианты решения задачи (5)-(6) при различных формах тяжести заболевания.

4. ЛПР должен выбрать из полученного множества решений задачи наиболее приемлемый вариант с учётом имеющейся степени тяжести протекания заболевания. Если вариант не выбран, то ЛПР должен скорректировать f*i  (вернуться к пункту 2) и заново рассчитать минимаксные варианты решения задачи.

5. Поиск прекратить. Вывести значения  f*i(u,αi), СТ и рекомендуемый вектор управления – u*=(u*1,...,u*n).

Итерационная процедура последовательной минимизации максимального отклонения значений локальных критериев от эталонов повторяется до тех пор, пока ЛПР не удовлетворят текущие результаты.

Предложенный алгоритм решения задачи, основанный на сочетании методов идеальной точки и гарантированного результата, позволяет эффективно решать такие задачи принятия решений, в которых значения локальных критериев характеризуются размытостью.

Выводы

Проведен обзор существующих моделей вирусных инфекций. Рассмотрены модели, которые характеризуют распространения эпидемии и модели, которые описывают распространение инфекции внутри организма человека. Приведена постановка многокритериальной нечёткой задачи принятия решений при выборе медикаментозной терапии. Рассмотрен алгоритм её решения, основанный на методах сведения нечётких задач к чётким через введение множеств уровня α.

В рамках проведенных исследований выполнено:

  1. Проанализированы особенности процесса протекания вирусного заболевания.
  2. Выполнен обзор существующих моделей прогноза динамики протекания и распространения вирусного инфекционного заболевания.
  3. Разработан алгоритм моделирования протекания вирусного заболевания, который поможет выбрать эффективное лечение. 

При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2014 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.

 

Рисунок 1 – Процесс заражения вирусными инфекциями 

Список источников

  1. Ющук Н.Д. Инфекционные болезни : учеб. для студ. мед. вузов / Н.Д. Ющук, Ю.Я. Венгеров. – М. : Медицина, 2003. – 544 с.: ил. – (Учеб.лит. для студ.мед.вузов).

  2. Кондратьев М. А Совершенствование методологии моделирования распространения инфекционных заболеваний // Вычислительные, измерительные и управляющие системы: сборник научных трудов.— СПб. : Изд-во Политехн. ун-та, 2011. – С. 37–44.

  3. Моделирование паротита. Модели кишечных [Электронный ресурс]. –  Режим доступа: www/ URL: http://meduniver.com/Medical/Microbiology/1152.html - Загл. с экрана.

  4. Марчук Г.И. Математические методы в клинической практике / Г.И. Марчук, Н.И. Нисевич. – Новособирс : Наука, 1978. – 120 с.

  5. Гамиева Е.В. Новые технологии в лечении бронхообструктивного синдрома у детей с острыми респираторными заболеваниями / Е.В. Гамиева, В.В. Лазарев // Вестник новых медицинских технологий. – 2009. – Т. XVI, № 3. – С. 190–191.

  6. Рыков. А.С. Модели и методы системного анализа: принятие решений и оптимизация : учебное пособие для вузов / А.С. Рыков. – М. : «МИСИС», Издательский дом «Руда и металлы», 2005. – 352 с.

  7. Андрейчин М.А. Медсистринство при інфекційних хворобах / М.А. Андрейчин, О.Л. Івахів. – Тернопіль : Укрмедкнига, 2002. – 385 с.
  8. Тимченко В.Н. Диагностика, дифференциальная диагностика и лечение детских инфекций : справочник / В.Н. Тимченко, В.В. Леванович. – 2-е изд. – СПб. : ЭЛБИ-СПб, 2007. – 384 c.
  9. Ющук Н.Д. Инфекционные болезни / Н.Д. Ющук, Ю.Я. Венгеров. – М. : Медицина, 2003. – 544 с.
  10. Селякова С.М. Нечеткая модель и алгоритм решения задачи выбора медикаментозной терапии / С.М. Селякова // Штучний інтелект. – 2013. – № 2. – С. 245–250.
  11. Сайт кафедры биомедицинской инженерии (БМИ) ХНУРЭ [Электронный ресурс]. – Режим доступа: http://nure.ua/university/structure/departments/et/bme/  
  12. Электронная библиотека ДонНТУ [Электронный ресурс]. – Режим доступа: http://ea.donntu.ru/handle/123456789/22962.
  13. Электронная библиотека ДонНТУ [Электронный ресурс]. – Режим доступа: http://ea.donntu.ru:8080/jspui/handle/123456789/22954.
  14. Электронная библиотека ДонНТУ [Электронный ресурс]. – Режим доступа: http://ea.donntu.ru:8080/jspui/handle/123456789/14195.

  15. Электронная библиотека ДонНТУ [Электронный ресурс]. – Режим доступа: http://ea.donntu.ru:8080/jspui/handle/123456789/12382.

  16. Сайт кафедры инфекционных болезней ДонНМУ [Электронный ресурс]. – Режим доступа: http://www.dsmu.edu.ua/departments/departmentss/clinicaldepartment-/102-2010-01-25-14-29-20 

  17. Кондратьев М.А. Разработка модели распространения инфекционных заболеваний на основе агентного подхода : автореферат дис. ... кандидата технических наук: 05.13.18 / М.А. Кондратьев ;  Федеральное государственное автономное образовательное учреждении высшего профессионального образования «Санкт-Петербургский государственный университет аэрокосмического приборостроения». – Санкт-Петербург, 2012. – 19 с.
  18. Гепатит A вирусных инфекций в США: оценки и последствия для иммунизации детей на основе модели [Электронный ресурс]. – Режим доступа: http://pediatrics.aappublications.org/content/109/5/839.short
  19. Шувалова Е.П. Инфекционные болезни / Шувалова Е.П. – Ростов н/Д : Феникс, 2001. – 959 с.

  20. Шлоссберг Д. Дифференциальная диагностика инфекционных болезней: Пер.с англ. / Д. Шлоссберг, И. А. Шульман. – М. : Бином; СПб. Невский диалект, 1999. – 318 с.
  21. Селякова С.М. Нечеткая модель и алгоритм решения задачи выбора медикаментозной терапии / С.М. Селякова // Штучний інтелект. – 2014. – № 2. – С. 75–80.