Русский   English
ДонНТУ   Портал магістрів

Реферат за темою випускної роботи

Зміст

Вступ

В екосистемі мешкає велика кількість організмів. Значна частина з цих організмів – мікроорганізми, які при попаданні в організм людини викликають негативний вплив. Проникнення однієї форми живих істот, переважно мікроорганізмів, у більш високоорганізовані організми позначають терміном «інфекція» [1].

Інфекційні хвороби є однією з важливих проблем сучасної медицини і залишаються найбільш небезпечними та поширеними. Єдину інфекційну хворобу, яку вдалося практично ліквідувати – вітряна віспа. У той час, як у світі налічується сотні інфекцій, з якими не відомий спосіб боротьби. Самими поширеними інфекціями є: холера, бубонна чума, грип, черевний тиф, вісп

Найчастіше за рік людина хворіє на вірусні інфекційні захворювання і це є причиною її тимчасової непрацездатності. Найбільшу групу ризику складають діти та особи репродуктивного віку. Від інфекційних хвороб щорічно помирає понад 16 млн. чоловік, тобто стільки ж, скільки сумарно від захворювань серцево-судинних і злоякісних утворень [1].

1. Актуальність теми

Сучасна медицина для своєї практики і теорії застосовує математичні, фізичні та технічні методи Це надає можливість не тільки поставити діагноз, а й встановити причину хвороби.

Розвиток та впровадження в медичну практику різноманітних методів досліджень частіше призводять до необхідності застосування математичних методів [4]. Тому на сьогоднішній день актуальними є наступні проблеми:

  1. Ефективної діагностики вірусного захворювання;
  2. Оцінки тяжкості та дослідження динаміки патологічного процесу протікання захворювання;
  3. Вибору та оцінки ефективності застосовуваної терапії ;
  4. Прогнозування протікання захворювання і ймовірних його результатів.

Таким чином, актуальність теми моделювання протікання вірусного захворювання полягає в необхідності робити прогноз для кожного пацієнта з урахуванням його вікових категорії, часу поширення вірусу в організмі і обсягу пошкоджених тканин для ефективного його лікування.

2. Мета і задачі дослідження

    Метою дослідження є розробка моделі процесу протікання вірусного захворювання, яка дозволила б врахувати індивідуальні характеристики пацієнта і тяжкість захворювання, і на підставі цього вибрати ефективне лікування.

    Для досягнення мети роботи необхідно виконати наступні завдання:

    1. Розглянути особливості процесу протікання вірусного захворювання.
    2. Виконати огляд існуючих моделей прогнозу динаміки протікання і розповсюдження вірусного інфекційного захворювання.
    3. Розробити динамічну модель протікання вірусного захворювання , яка допоможе вибрати ефективне лікування.

    Об'єкт дослідження: вірусне захворювання, його днаміка та лікування.

    Предмет дослідження: існуючі моделі динаміки перебігу вірусного захворювання і методи лікування та діагностики.

3. Огляд існуючих математичних моделей вірусних захворювань

Існує два основних напрямки розповсюдження вірусного захворювання. До першого напрямку слід віднести поширення епідемії, а другий напрямок – ураження інфекцією конкретної людини. Перший напрямок має велике соціально-економічне значення для суспільства і держави. Воно використовується для прогнозу та моделювання епідемії в динаміціі. Другий же напрям робить акцент на моделюванніаний підхід до моделювання призначене для прогнозу та ефективного лікування пацієнта.

3.1 Огляд міжнародних джерел

Для отримання оперативної інформації про стан зараженого організму та з метою прогнозування подальшого розповсюдження інфекції застосовують методи математичного моделювання. Значна частина моделей розповсюдження захворювань заснована на використанні алгебро-диференціальних рівняння. Найбільш відомою серед таких є SIR-модель, запропонована В.А. Керманом і А.Г. Мак-Кендриком. У цій моделі, як і в інших моделях такого типу, всі популяції модельованої території ділиться на групи: «Susceptible» – здорові люди, сприйнятливі до захворювання (позначають їх кількість S), «Infectious» – інфекційні хворі (позначають їх кількість I), «Recovered» – ті, які перехворіли модельованим захворюванням, і більш до нього не сприйнятливі (позначають їх кількість R). Враховуючи, що загальне число індивідів в популяції не змінюється, приріст кількост людей в кожній із виділинних груп можно описати наступними рівняннями: dS/dt=-βSI;  dI/dt=βSI-γI; dR/dt=-γI, де γ і β – інтенсивність контактів і одуження [177].

Грегорі Л. Армстронг, Бет П. Белл в роботі "Вірусний гепатит A в США: оцінки і наслідки для імунізації дітей на основі моделі" переставали результати, які дозволяють істотно знизити захворюваність на гепатит в цілому [18].

У Харківському національному університеті радіоелектроніки (ХНУРЕ) на кафедрі біомедичної інженерії (БМІ) займаються науковою діяльністю за наступними напрямками: дослідження в областях мікропроцесорних та мікроконтролерних систем, обробка медичних зображень і сигналів, розробка програмно-апаратного забезпечення нейрохірургічних систем, дослідження інформаційних технологій в медицині, математичне моделювання та приладобудування в медицині, створення біомедичних систем, оптимізація створення цифроаналогових пристроїв, дослідження електрохемілюмінесценціі і нанофотоніки, формування та аналіз акустичних полів природного і техногенного походження [111].

У Донецькому національному університеті функціонує кафедра інфекційних хвороб. Співробітники кафедри займаються лікуванням хворих у клініці, консультативної роботою в відділеннях лікарні, гепатологічних Центрі, здійснюють виїзди по лінії екстреної медичної допомоги в міста і райони області. На базі кафедри створено і функціонує Донецьке обласне науково-медичне товариство інфекціоністів. Основною метою діяльності Товариства є підвищення рівня науково-медичної підготовки практичних лікарів Донецької області. Основними напрямками наукової діяльності кафедри є вірусні гепатити, інфекції центральної нервової системи та TORCH-інфекції. При кафедрі був організований перший в Україні Центр Консультативної і Лікувально-діагностичної допомоги хворим вірусними гепатитами [16].

З метою короткострокового прогнозування захворюваності на епідемічний паротит і вітряною віспою В.Д. Денисенко (1982) використовував математичний апарат автокореляції, що описує характер багаторічних і внутрішньорічних коливань епідемічного процесу. Прогнозування проводилося на основі даних щомісячної захворюваності в 9 великих містах України за 10-11 років. Ця модель в порівнянні з розглянутими вище, реалізує формальний підхід до прогнозування епідемічного процесу і тому в меншій мірі відповідає пропонованим в таких випадках вимогам [3] .

Модель С.Г. Кривенкова і Ю.П. Рикушіна для паротиту заснована на системі диференціальних рівнянь з відхиляющімся аргументом (ДУОА) [3]. Для моделювання епідеміологічного процесу використовують декілька класів моделювання: формальну апроксимацію (наближення), формальну екстраполяцію (в основному кривих захворюваності) і змістовне моделювання епідемічного процесу з дискретним або безперервним перебігом [3]. Моделювання протікання вірусного захворювання в організмі людини за допомогою системи нелінійних звичайних диференціальних рівнянь представлено в джерелі [4].

3.3 Огляд локальних джерел

  1. "Варіанти класифікації за байесу для прогнозу розвитку пневмонії при гострих отруєннях психотропними засобами" автори: Єлькою А.Н., Ільяшенко К.К. [122].
  2. "Побудова запитів до бази медичних рентгенівських знімків на основі аналізу векторного представлення зображень" автори: Бовирін А.В., Губанов А.В., Колесов А.І., Курякін В.Ф., Родюшкін К.В., Чудинович Б.М. [13].
  3. "Pазрабка спеціалізованої комп'ютерної системи обробки томограм для діагностики захворювання підшлункової залози" автор Дейнега М.Ф. [14] .
  4. " Лікувльне та профілактичне плавання при захворюваннях сколіозом" автори: Семенова Н.Л., Cухарева Л.В. , Стойка Р.В. [15].

    4. Рішення задач і результати досліджень

    Система нелінійних звичайних диференціальних рівнянь, яка описує динаміку вірусного захворювання [4], представлена ​​у виразі (1):

    где βVdt – приріст числа вірусів dV за інтервал часу dt;

    γFVdt – описує число вірусів,, які нейтралізуються антитілами F;

    τ – час, протягом якого здійснюється формування каскаду плазмових клітин;

    α – коефіцієнт, що враховує ймовірність, з якою один антиген здатний викликати реакцію організму;

    p – константа;

    C – імунологічний рівень плазмових клітин в організмі;

    ρCdt – генерація антитіл плазмовими клітинами;

    ηγVF –враховує зменшення числа антитіл в інтервалі часу за рахунок зв'язку з антигенами і виходом з подальшої активної боротьби;

    μf – коефіцієнт, обернено пропорційний часу розпаду антитіла;

    dm – описує зміну ураженої тканини;

    σVdt – тканина організму, яка була зруйнована вірусами;

    μmmdt – тканина, яка може бути відновлена за рахунок діяльності організму.

    Основними діючими фактурами вірусного захворювання є: кількість вірусів в організмі V, число плазмових клітин C, які виробляють антитіла F, і маса пошкоджених вірусами тканини M. Перше рівняння системи (1) описує зміну числа вірусів в організмі. Друге рівняння системи (1) визначає зростання плазмових клітин C. Третє рівняння системи (1) дозволяє підрахувати баланс числа антитіл даної структури, що реагують з антитілами вірусу. Останнє рівняння з моделі характеризує баланс пошкодженої тканини організму при даному захворюванні [4].

    Нехай є математична модель прогноза зміни стану пацієнта в результаті застосування медикаментозної терапії:

    zi=fi(u1,...,un;αi), i=1,...,m,                                                  (2)

    де αi

    Обмеження, накладені на складові векторів u і z, які визначають їх допустимі галузі вимірювання, представимо у наступному вигляді:

    gj(u,z)≥0, j=1,...,J.                                                          (3)

    Приватні цільові функції fi(u1,...,un;αi), i=1,...,m складають векторну функцію fі розрізняються своїми коефіцієнтами відносної важливості (вагами) (γ1,...,γm), значення яких можуть змінюватися.

    Треба знайти вектор управління u*=(u*1,...,u*n), що забезпечує найкраще наближення до бажаних значень локальних критеріїв f*i :

    де fi(u,αi) – нечіткі локальні критерії, значення яких обчислюються по моделям;

    f*i – бажані (ідеальні) значення локальних критеріїв, що задаються ОПР;

    gj(u) – обмеження на складові вектора u;

    bj – задані числа;

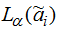    – множина рівня α нечітких параметрів 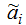, запроваджене для обліку нечіткості параметрів αi.

    В якості вектора керуючих параметрів u= (u1,...,un) виступає набір дозувань n препаратів, які призначається базовою та інгаляційної терапією.

    Нечіткі параметри αi задамо у вигляді лінгвістичних змінних, які буде характеризувати тяжкість захворювання. Припустимо, αi

    Ефективність лікування, як правило, оцінюється за наступними критеріями [7]: вираженість основних симптомів (f1), поліпшення стану пацієнта при аналізі катамнеза (f2), імуномодулюючий ефект проведеної терапії (f3), які складають векторну функцію f і різняться вагами. Значення функції f1 визначається в результаті огляду лікаря, f3 – за допомогою аналізу імунограми. А функцію f2 пропонується спрогнозувати з урахуванням форми тяжкості захворювань.

    Для вирішення подібних завдань доцільно використовувати підхід, заснований на принципі гарантованого результату [8]. У цьому випадку проводиться мінімізація найбільшого відхилення нечітких значень локальних критеріїв від їх еталонних значень при виконанні накладених обмежень:

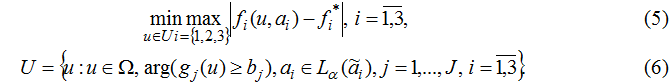
    При нечітких обмеженнях в задачі (5)-(6) необхідно побудувати функцію належності μj(u), j=1,J виконання кожного з обмежень g j≥bj, j=1,J..

    Доцільність мінімаксної постановки задачі прийняття рішень можна пояснити тим, що призначена терапія повинна забезпечувати гарантований результат одужання пацієнта.

    Дану задачу багатокритеріальної оптимізації в умовах невизначеності можна звести до задачі багатокритеріальної оптимізації на основі множин рівня α, що дозволить здійснити пошук раціональних варіантів вирішення по вибираним критеріям [8].

    Пропонується використовувати наступний алгоритм вирішення задачі:

    1. Виділити діапазони значень α для різних ступенів тяжкості протікання захворювання. Наприклад, можуть бути виділені наступні ступені тяжкості (СТ) захворювання:

      СТ=1, при 0,7≤α≤1,0 – важкій формі;

      СТ=2, при 0,3≤α≤0,7 – середня форма;

      СТ=3, при 0,0≤α≤0,3 – легка форма.

    2. ОПР повинен призначити бажані (еталонні) значення локальних критеріїв f*i.
    3. Розрахувати мінімаксні (гарантовані) варіанти рішення задачі (5)-(6) при різних формах важкості захворювання.
    4. ОПР повинен вибрати з отриманого безлічі рішень задачі найбільш прийнятний варіант з урахуванням наявної ступеня тяжкості протікання захворювання. Якщо варіант не обраний, то ОПР має скоригувати f*i (повернутися до пункту 2) і заново розрахувати мінімаксні варіанти вирішення завдання.
    5. Пошук припинити. Вивести значення f*i(u,αi), СТ і рекомендований вектор управління – u*=(u*1,...,u*n). 

    Ітераційна процедура послідовної мінімізації максимального відхилення значень локальних критеріїв від еталонів повторюється доти, поки ОПР не задовольнить поточні результати.

    Запропонований алгоритм вирішення задачі, заснований на поєднанні методів ідеальної точки і гарантованого результату, дозволяє ефективно вирішувати такі задачі прийняття рішень, в яких значення локальних критеріїв характеризуються розмитістю.

    Висновки

    Проведено огляд існуючих моделей вірусних інфекцій. Розглянуто моделі, які характеризують поширення епідемії та моделі, які описують поширення інфекції всередині організму людини. Наведено постановку багатокритеріальної нечіткої задачі прийняття рішень при виборі медикаментозної терапії. Розглянуто алгоритм її вирішення, заснований на методах відомості нечітких задач до чітких через введення множин рівня α .

    У рамках проведених досліджень виконано:

    1. Проаналізовано особливості процесу протікання вірусного захворювання.
    2. Виконано огляд існуючих моделей прогнозу динаміки протікання і розповсюдження вірусного інфекційного захворювання.
    3. Розроблено алгоритм моделювання протікання вірусного захворювання, який допоможе вибрати ефективне лікування.

    При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: грудень 2014 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.

     

    Рисунок 1 – Процес заражения вирусом

    Перелік посилань

      1. Ющук Н.Д. Инфекционные болезни : учеб. для студ. мед. вузов / Н.Д. Ющук, Ю.Я. Венгеров. – М. : Медицина, 2003. – 544 с.: ил. – (Учеб.лит. для студ.мед.вузов).

      2. Кондратьев М. А Совершенствование методологии моделирования распространения инфекционных заболеваний // Вычислительные, измерительные и управляющие системы: сборник научных трудов.— СПб. : Изд-во Политехн. ун-та, 2011. – С. 37–44.

      3. Моделирование паротита. Модели кишечных [Электронный ресурс]. –  Режим доступа: www/ URL: http://meduniver.com/Medical/Microbiology/1152.html - Загл. с экрана.

      4. Марчук Г.И. Математические методы в клинической практике / Г.И. Марчук, Н.И. Нисевич. – Новособирс : Наука, 1978. – 120 с.

      5. Гамиева Е.В. Новые технологии в лечении бронхообструктивного синдрома у детей с острыми респираторными заболеваниями / Е.В. Гамиева, В.В. Лазарев // Вестник новых медицинских технологий. – 2009. – Т. XVI, № 3. – С. 190–191.

      6. Рыков. А.С. Модели и методы системного анализа: принятие решений и оптимизация : учебное пособие для вузов / А.С. Рыков. – М. : «МИСИС», Издательский дом «Руда и металлы», 2005. – 352 с.

      7. Андрейчин М.А. Медсистринство при інфекційних хворобах / М.А. Андрейчин, О.Л. Івахів. – Тернопіль : Укрмедкнига, 2002. – 385 с.
      8. Тимченко В.Н. Диагностика, дифференциальная диагностика и лечение детских инфекций : справочник / В.Н. Тимченко, В.В. Леванович. – 2-е изд. – СПб. : ЭЛБИ-СПб, 2007. – 384 c.
      9. Ющук Н.Д. Инфекционные болезни / Н.Д. Ющук, Ю.Я. Венгеров. – М. : Медицина, 2003. – 544 с.
      10. Селякова С.М. Нечеткая модель и алгоритм решения задачи выбора медикаментозной терапии / С.М. Селякова // Штучний інтелект. – 2013. – № 2. – С. 245–250.
      11. Сайт кафедры биомедицинской инженерии (БМИ) ХНУРЭ [Электронный ресурс]. – Режим доступа: http://nure.ua/university/structure/departments/et/bme/  
      12. Варианты классификации по байесу для прогноза развития пневмонии при острых отравлениях психотропными средства [Электронный ресурс]. – Режим доступа: http://ea.donntu.ru/handle/123456789/22962.
      13. Построение запросов к базе медицинских рентгеновских снимков на основе анализа векторного представления изображений [Электронный ресурс]. – Режим доступа: http://ea.donntu.ru:8080/jspui/handle/123456789/22954.
      14. Pазработка специализированной компьютерной системы обработки томограмм для диагностики заболевания поджелудочной железы [Электронный ресурс]. – Режим доступа: http://ea.donntu.ru:8080/jspui/handle/123456789/14195.

      15. ЛІКУВАЛЬНЕ ТА ПРОФІЛАКТИЧНЕ ПЛАВАННЯ ПРИ ЗАХВОРЮВАННЯХ СКОЛІОЗОМ [Электронный ресурс]. – Режим доступа: http://ea.donntu.ru:8080/jspui/handle/123456789/12382.

      16. Сайт кафедры инфекционных болезней ДонНМУ [Электронный ресурс]. – Режим доступа: http://www.dsmu.edu.ua/departments/departmentss/clinicaldepartment-/102-2010-01-25-14-29-20 

      17. Кондратьев М.А. Разработка модели распространения инфекционных заболеваний на основе агентного подхода : автореферат дис. ... кандидата технических наук: 05.13.18 / М.А. Кондратьев ;  Федеральное государственное автономное образовательное учреждении высшего профессионального образования «Санкт-Петербургский государственный университет аэрокосмического приборостроения». – Санкт-Петербург, 2012. – 19 с.
      18. Гепатит A вирусных инфекций в США: оценки и последствия для иммунизации детей на основе модели [Электронный ресурс]. – Режим доступа: http://pediatrics.aappublications.org/content/109/5/839.short
      19. Шувалова Е.П. Инфекционные болезни / Шувалова Е.П. – Ростов н/Д : Феникс, 2001. – 959 с.

      20. Шлоссберг Д. Дифференциальная диагностика инфекционных болезней: Пер.с англ. / Д. Шлоссберг, И. А. Шульман. – М. : Бином; СПб. Невский диалект, 1999. – 318 с.
      21. Селякова С.М. Нечеткая модель и алгоритм решения задачи выбора медикаментозной терапии / С.М. Селякова // Штучний інтелект. – 2014. – № 2. – С. 75–80.