DonNTU   Masters' portal

Iryna Chystikova

Faculty of computer science and technology (CST)

Department of System analysis and modeling

Speciality System analysis and control

Modeling of current viral disease

Scientific adviser: Ph.D., Docent Svetlana Selyakova

Resume Abstract

Abstract

Content

• Introduction
• 1. Theme urgency
• 2. Goal and tasks of the research
• 3. Researches overview
• Conclusion
• References

Introduction

The huge number of organisms lives in an ecosystem. A considerable part of these organisms – microorganisms which, when ingested, are causing a negative impact. Penetration of one form of living beings, mainly microorganisms, more highly organisms termed "infection" [1].

Infectious diseases is one of the most important problems of modern medicine and remain the most dangerous and widespread. The only infectious disease that have been practically eliminated – varicella. In the world there are hundreds of infections that do not know the way to fight. By the common infections are: cholera, bubonic plague, influenza, typhoid, smallpox.

The person is ill on viral infectious diseases in a year and it is the reason of its temporary disability. Children and personality of reproductive age constitute the greatest risk. From infectious diseases kills more than 16 million people, that is the same as total from cardiovascular diseases and malignant tumors [1].

1. Theme urgency

The modern medicine applies mathematical, physical and technical methods that gives the chance not only to make the diagnosis, but also to establish an etiology to the practice and the theory.

Development and introduction in medical practice of various methods of researches even more often result now in need of application of mathematical methods [4]. Therefore today actual is the following problems:

• effective diagnostics of a viral disease;
• estimates of weight and research of dynamics of pathological process of course of a disease;
• choice and assessment of efficiency of applied therapy;
• forecasting of course of a disease and its probable outcomes.

2. Goal and tasks of the research

Research objective development of model of process of course of a viral disease. It is model has to consider individual characteristics of the patient and weight of a disease. On the basis of what to choose effective treatment.

Main tasks of the research:

1. Consider the features of the process flow of viral disease.
2. Analyses the existing automated systems of modeling of a viral disease.
3. Develop algorithm of modeling of course of a viral disease which will help to choose effective treatment.

Research object: viral disease, its diagnostics and treatment.

Research subject: prediction model of the dynamics of the disease.

3. Researches overview

The system of nonlinear ordinary differential equations which describes the dynamics of viral diseases [4], is presented in equation (1):



where βVdt – gain of number of the viruses dV for an interval of time of dt;

γFVdt – describes the number of viruses neutralized by antibodies F;

τ – time during which the formation stage of plasma cells;

α – coefficient taking into account the probability with which one is able to initiate an antigen response of the organism;

p – constant;

C – immunological level of plasma cells in the body;

ρCdt – generation of antibodies by plasma cages;

ηγVF – considers reduction of number of antibodies in an interval due to communication with anti-genes and an exit from further active fight;

μ_f – coefficient is inversely proportional to the decay time of the antibody;

dm – describes the change of the affected tissue;

σVdt – tissue of the body, which was destroyed by viruses;

μ_mmdt – tissue recovered due to the activity of the organism.

The main active invoices viral disease are: the amount of virus in the body V, the number of plasma cells C, producing antibodies F, viruses and damaged tissue mass M. The first equation (1) describes the change in the number of viruses in the body. The second equation of system (1) determines the growth of plasma cells C. The third equation of (1) allows you to calculate the balance of the number of antibodies of this structure , antibodies reactive with the virus. The last equation of the model describes the balance of the damaged tissues of the body in this disease [4].

Suppose that there are mathematical models predict change the patient's condition as a result of drug therapy:

z_i=f_i(u₁,...,u_n;α_i), i=1,...,m,                                                      (2)

where α_i – fuzzy parameters, characterizing the severity of the disease.

Restrictions:  

g_j(u,z)≥0, j=1,...,J.                                                       (3)

Private target functions f_i(u₁,...,u_n;α_i), i=1,...,mcomponent of the vector function f.

Control vector u*=(u^*₁,...,u^*_n) is required to find that will provide the best approximation to the desired values of local criteria f^*_i:



where f_i(u,α_i) – fuzzy local criteria, values are calculated by the model;

f^*_i– desirable (perfect) the values of the local criteria set by the person who makes the decision;

g_j(u) – restrictions on the vector u;

b_j – the set numbers;

– the level set α.

u= (u₁,...,u_n) – vector of operating parameters. This vector is a set of dosages for n preparation.

Fuzzy parameters α_i specified in the form of a linguistic variable. This variable corresponds to the severity of the disease. Suppose that linguistic variable consists of three variables. this corresponds to mild, moderate and severe forms of disease. Efficiency of treatment is estimated by the following criteria: expressiveness of the main symptoms (f₁), condition of the patient in the analysis cattiness (f₂), immunomodulating effect (f₃). They constitute the function f. The f₂ function is offered to be predicted taking into account a form of weight of diseases.

Use the approach guaranteed result [8].



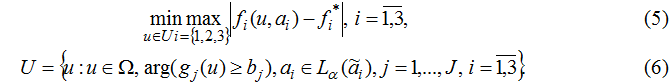
When fuzzy constraints in the problem (5)-(6) is necessary to construct the membership function μ_j(u), j=1,J.

It is offered to use the following algorithm of the solution of a task:

1. Select ranges of values α for different degrees of severity of the disease. For example, you may have the following severity (S) of the disease:

   S=1, при  0,7≤α≤1,0 - severe form;

   S=2, при 0,3≤α≤0,7 - average form;

   S=3, при 0,0≤α≤0,3 - easy form.

2. Set value of local criteria of f^*_i.
3. Calculate guaranteed solutions to the problem (5)-(6) in various forms of severity of bronchial obstruction.
4. Choose the most acceptable option from the received set of solutions of a task. If the option isn't chosen, the decision-maker has to correct f^*_i (to return to point 2).
5. Remove values f^*_i(u, α_i), S and a recommended vector of management – u * = (u*₁... u*_n).

The proposed algorithm for solving the problem based on a combination of an ideal point and guaranteed result.

Conclusion

Master's work is devoted to actual medical problem. In a study carried out:

1. Relevance of a perspective is considered
2. Features of process of course of a viral disease are analyzed;
3. The algorithm of modeling of course of a viral disease is developed.

During writing this essay master's work is not yet complete. Final completion: December 2014. Full text of the work and materials on the topic can be obtained from the author or his head after that date.

According to the problem, the direction of future research - selection, development and adaptation of mathematical models of its software implementation and testing.



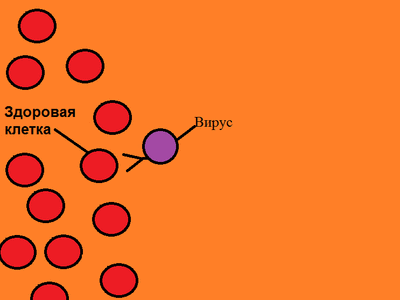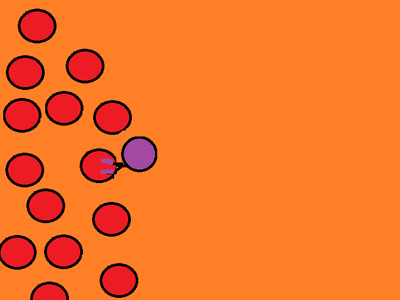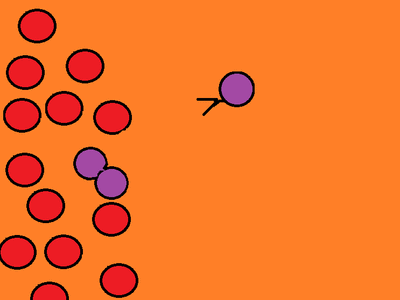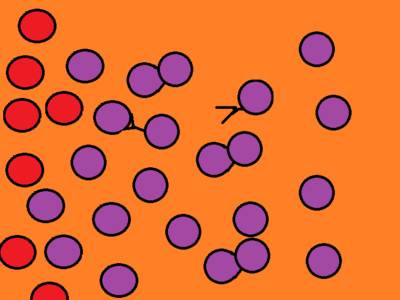
Figure 1 – The process of spread of the virus

References

1. Ющук Н.Д. Инфекционные болезни : учеб. для студ. мед. вузов / Н.Д. Ющук, Ю.Я. Венгеров. – М. : Медицина, 2003. – 544 с.: ил. – (Учеб.лит. для студ.мед.вузов).

2. Кондратьев М. А Совершенствование методологии моделирования распространения инфекционных заболеваний // Вычислительные, измерительные и управляющие системы: сборник научных трудов.— СПб. : Изд-во Политехн. ун-та, 2011. – С. 37–44.

3. Моделирование паротита. Модели кишечных [Электронный ресурс]. –  Режим доступа: www/ URL: http://meduniver.com/Medical/Microbiology/1152.html - Загл. с экрана.

4. Марчук Г.И. Математические методы в клинической практике / Г.И. Марчук, Н.И. Нисевич. – Новособирс : Наука, 1978. – 120 с.

5. Гамиева Е.В. Новые технологии в лечении бронхообструктивного синдрома у детей с острыми респираторными заболеваниями / Е.В. Гамиева, В.В. Лазарев // Вестник новых медицинских технологий. – 2009. – Т. XVI, № 3. – С. 190–191.

6. Рыков. А.С. Модели и методы системного анализа: принятие решений и оптимизация : учебное пособие для вузов / А.С. Рыков. – М. : «МИСИС», Издательский дом «Руда и металлы», 2005. – 352 с.

7. Андрейчин М.А. Медсистринство при інфекційних хворобах / М.А. Андрейчин, О.Л. Івахів. – Тернопіль : Укрмедкнига, 2002. – 385 с.
8. Тимченко В.Н. Диагностика, дифференциальная диагностика и лечение детских инфекций : справочник / В.Н. Тимченко, В.В. Леванович. – 2-е изд. – СПб. : ЭЛБИ-СПб, 2007. – 384 c.
9. Ющук Н.Д. Инфекционные болезни / Н.Д. Ющук, Ю.Я. Венгеров. – М. : Медицина, 2003. – 544 с.
10. Селякова С.М. Нечеткая модель и алгоритм решения задачи выбора медикаментозной терапии / С.М. Селякова // Штучний інтелект. – 2013. – № 2. – С. 245–250.
11. Сайт кафедры биомедицинской инженерии (БМИ) ХНУРЭ [Электронный ресурс]. – Режим доступа: http://nure.ua/university/structure/departments/et/bme/  
12. Варианты классификации по байесу для прогноза развития пневмонии при острых отравлениях психотропными средства [Электронный ресурс]. – Режим доступа: http://ea.donntu.ru/handle/123456789/22962.
13. Построение запросов к базе медицинских рентгеновских снимков на основе анализа векторного представления изображений [Электронный ресурс]. – Режим доступа: http://ea.donntu.ru:8080/jspui/handle/123456789/22954.
14. Pазработка специализированной компьютерной системы обработки томограмм для диагностики заболевания поджелудочной железы [Электронный ресурс]. – Режим доступа: http://ea.donntu.ru:8080/jspui/handle/123456789/14195.

15. ЛІКУВАЛЬНЕ ТА ПРОФІЛАКТИЧНЕ ПЛАВАННЯ ПРИ ЗАХВОРЮВАННЯХ СКОЛІОЗОМ [Электронный ресурс]. – Режим доступа: http://ea.donntu.ru:8080/jspui/handle/123456789/12382.

16. Сайт кафедры инфекционных болезней ДонНМУ [Электронный ресурс]. – Режим доступа: http://www.dsmu.edu.ua/departments/departmentss/clinicaldepartment-/102-2010-01-25-14-29-20 

17. Кондратьев М.А. Разработка модели распространения инфекционных заболеваний на основе агентного подхода : автореферат дис. ... кандидата технических наук: 05.13.18 / М.А. Кондратьев ;  Федеральное государственное автономное образовательное учреждении высшего профессионального образования «Санкт-Петербургский государственный университет аэрокосмического приборостроения». – Санкт-Петербург, 2012. – 19 с.
18. Гепатит A вирусных инфекций в США: оценки и последствия для иммунизации детей на основе модели [Электронный ресурс]. – Режим доступа: http://pediatrics.aappublications.org/content/109/5/839.short
19. Шувалова Е.П. Инфекционные болезни / Шувалова Е.П. – Ростов н/Д : Феникс, 2001. – 959 с.

20. Шлоссберг Д. Дифференциальная диагностика инфекционных болезней: Пер.с англ. / Д. Шлоссберг, И. А. Шульман. – М. : Бином; СПб. Невский диалект, 1999. – 318 с.
21. Селякова С.М. Нечеткая модель и алгоритм решения задачи выбора медикаментозной терапии / С.М. Селякова // Штучний інтелект. – 2014. – № 2. – С. 75–80.