На момент публікації даного реферату робота над магістерською дисертацією ще не завершена. Остаточний варіант роботи буде доступний у грудні 2014 року. Текст дисертації та матеріали за темою можна отримати, зв'язавшись з автором або його науковим керівником.

Зміст

Введение
Актуальность темы
Цель и задачи исследования
Обзор исследований и разработок
Выводы
Список источников

1. Вступ

Головна роль у вирішенні завдання синтезу реалістичних (переконливих) зображень віртуальних сцен відведена алгоритмам візуалізації. Сьогодні найбільш поширеними є алгоритми візуалізації, що базуються на принципі растеризації 3D-сцени (з проміжними етапами тонування), однак синтезовані за їх допомогою зображення не можна назвати ні фотореалістичними, ні, тим паче, фізично чітким. Проте, порівняно з алгоритмами трасування променів, ці алгоритми є менш вимогливими до ресурсів і добре вписуються в рамки SIMD-архітектури, що лежить в основі сучасних GPU, тому широко використовуються в системах інтерактивної віртуальної реальності.

Алгоритми трасування променів використовуються для фізичного моделювання процесу поширення світла в середовищі і його взаємодії з об'єктами віртуальних сцен. Таким чином, ступінь реалістичності синтезованого зображення обмежена (здебільшого) лише знаннями про поведінку світла. Процес моделювання надзвичайно ресурсоємний, тому трасування променів переважно застосовується для статичної візуалізації. Проте зростання продуктивності сучасного апаратного забезпечення все частіше вдається досягти інтерактивних частот візуалізації за допомогою трасування променів. Перспектива витіснення алгоритмів растеризації алгоритмами трасування променів стає дедалі очевиднішою.

2. Актуальність теми

Попри наявність загального завдання синтезу реалістичного зображення, існує багато алгоритмів трасування променів, орієнтованих на вирішення вужчих завдань. Деякі алгоритми дозволяють виконати фізично чітке моделювання поведінки світла, завдяки чому можливе їх використання спільно з радіометричними системами, інші можуть навмисно порушувати фізичні закони (зокрема, закон збереження енергії), щоб надати більшої гнучкості дизайнерам і візуалізаторам, а також прискорити процес моделювання у системах реального часу. Таким чином, комп'ютерна візуалізація за допомогою трасування променів може застосовуватися і у галузі розваг (кінематограф, ігри), і у галузі навчання (симулятори), і у галузі моделювання (архітектурна візуалізація, моделювання поширення світлової енергії), і для візуалізації даних та реконструкції (медицина).

Сьогодні існує багато систем, що дозволяють трасувати віртуальні сцени інтерактивно або навіть в режимі реального часу, проте вони часто накладають деякі обмеження на трассируемого сцени. Наприклад, обмеженнями можуть бути відсутність підтримки анімації, домінування певних видів матеріалів (оскільки інші опрацьовуються повільніше або не підтримуються алгоритмом), формат представлення геометрії сцени, кількість об'єктів у сцені й їх складність, інтер'єрна чи екстер'єрна сцена.

3. Мета і завдання дослідження

Мета роботи — вивчення і аналіз існуючих алгоритмів трасування променів і шляхів підвищення їх ефективності для реалізації на GPU.

У роботі вирішуються наступні завдання:

Аналіз існуючих алгоритмів трасування променів і їх характеристик;
Аналіз існуючих технік прискорення трасування променів;
Аналіз способів реалізації алгоритмів трасування променів і технік їх прискорення на SIMD-архітектурах обчислювальних систем;
Модифікація алгоритму трасування променів і його відображення на архітектуру GPU з підтримкою теїнології CUDA

Об'єкт дослідження: алгоритми трасування променів.

Предмет дослідження: підвищення ефективності алгоритмів трасування променів і їх паралельна реалізація на архітектурі GPU-CUDA.

4. Огляд досліджень і розробок

Вивченню алгоритмів трасування променів, їх теоретичних основ, способів їх прискорення і варіантів відображення на паралельні архітектури присвячено багато досліджень. Під час аналізу предметної галузі, автор виокремив три основні напрямки досліджень:

Вдосконалення алгоритмів трасування променів;
Розробка спеціалізованого апаратного забезпечення;
Підвищення продуктивності апаратного забезпечення загального призначення

До першої групи віднесені дослідження, спрямовані на розробку концептуально нових алгоритмів трасування променів і відповідного математичного апарату, більш дрібні модифікації існуючих алгоритмів, розробка нових прискорюючих технік і модифікація існуючих. Група також містить модифікації алгоритмів трасування променів і технік їх прискорення для відображення на паралельні архітектури.

Решта груп об'єднує дослідження, які меншою мірою стосуються алгоритмічних основ методів трасування променів і націлені на розробку нового апаратного забезпечення.

Актуальною також залишається класифікація [1], запропонована Джеймсом Арво (James Arvo) і Девідом Кірком (David Kirk) (рис. 1). Дана класифікація може розглядатися як деталізація першого пункту варіанту класифікації, наведеного вище.

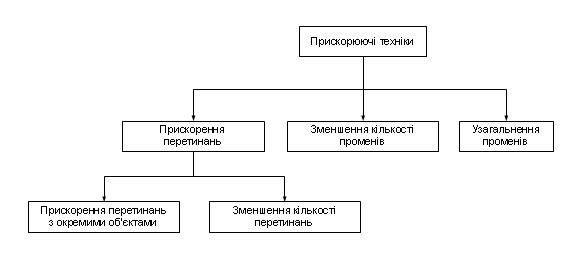
Класифікація технік прискорення візуалізації просторових сцен за принципом трасування променів

4.1 Огляд міжнародних джерел

Насамперед необхідно відзначити, що під час опрацювання різних тематичних матеріалів була помічена неоднозначність у використанні понять прямого і зворотного трасування променів. У даній роботі під зворотним трасуванням променів мається на увазі трасування від сенсора (камери, ока) до джерела освітлення.

4.1.1 Теоретичні основи алгоритмів трасування променів

Нехай картинна площина є частиною сцени, що візуалізується, і позначена Μ_s. Інтенсивність каналу λ_c j-го пікселя синтезованого зображення, якому у відповідність поставлена деяка ділянка Μ_j картинної площини визначається наступним рівнянням [2]:

$I_{j}\left(\lambda_{c} \right ) = \int_{\left ( x, \omega_{i}, \lambda \right ) \in M_{j} \times S^{2} \times \Lambda_{c} } W_{e}^{\left( j \right )}\left( x \leftarrow \omega_{i}, \lambda \right)L_{i}\left( x \leftarrow \omega_{i}, \lambda \right)\left | cos\left(\theta_{i}\right ) \right | dA\left( x\right) d\sigma\left(\omega_{i}\right )d\lambda$

Область інтегрування у правій частині рівняння задається декартовим добутком наступних множин:

Μ_j — множина точок картинної площини, що відповідають j-му пікселю зображення;
S² — множина точок, що лежать на поверхні сфери одиничного радіуса (кожна точка задає напрям падаючого світла);
Λ_c — множина довжин хвиль, що відповідають каналу λ_c зображення, є підмножиною множини довжин хвиль видимого спектра електромагнітного випромінювання, Λ_c∈Λ

Під знаком інтеграла використані наступні позначення:

L_i(x ω_i, λ) — енергетична яскравість освітлення з довжиною хвилі λ, що падає на точку x∈Μ_j j-го пікселя у напрямку -ω_i;
$W^{\left ( j\right)}_{e}$ (x ω_i, λ) — функція відгуку j-го пікселя на падаюче освітлення, що масштабує значення функції L_i(xω_i, λ);
θ_i — кут між нормаллю картинної площини у точці x і вектором ω_i;
Α(x) — міра площі, задана на множині Μ_j;
σ(ω_i) — міра площі, що задана на множині S² (оскільки сфера S² має одиничний радіус, дана міра визначає величину тілесного кута);
dλ — диференціальна міра довжини, задана на множині Λ_c

У рівнянні (1) невідома функція L_i(x ω_i, λ). Щоб знайти значення даної функції, необхідно розв'язати рівняння, що було вперше запропоноване в роботі [3], рівняння рендеринга, яке у більш загальному випадку має наступний вигляд:

$L_{o}\left( x \rightarrow \omega_{o}, \lambda \right ) = L_{e}\left(x \rightarrow \omega_{o}, \lambda\right) \right ) + \int_{\left ( \omega_{i}, \lambda \right ) \in \times S^{2} \times \Lambda_{c} } f_{s}\left( x, \omega_{i} \rightarrow \omega_{o}, \lambda \right)L_{o}\left( r_{M} \left( x, \omega_{i} \right ) \rightarrow -\omega_{i}, \lambda \right)\left | cos\left(\theta_{i}\right ) \right | d\sigma\left(\omega_{i}\right )d\lambda$

У рівнянні (2) використані наступні позначення:

L_o(x ω_o, λ) — енергетична яскравість освітлення з довжиною хвилі λ, що виходить з точки x∈Μ у напрямку ω_o, де Μ позначає множину точок всіх поверхонь сцени;
L_e(x ω_o, λ) — енергетична яскравість освітлення з довжиною хвилі λ, що випромінюється точкою x у напрямку ω_o;
f_s(x, ω_i ω_o, λ) — BSDF (Bidirectional Scattering Distribution Function), визначає частину світлової енергії з довжиною хвилі λ, перенесеної у точку x з напрямку ω_i, що буде відображена у напрямку ω_o;
r_Μ(x, ω_i) — функція, яка повертає першу точку перетину променя, що виходить з точки x у напрямку ω_i, з поверхнями Μ візуалізуємої сцени;

Рівняння (2) є інтегральним рівнянням другого порядку, оскільки невідома функція L_o(x ω_o, λ) зустрічається і під знаком інтеграла, і поза інтегрального оператора. Рівняння (2) базується на наступному твержденні: у разі відсутності перешкод, з якими фотони могли б взаємодіяти, енергетична яскравість на шляху від однієї поверхні до іншої не змінюється, тобто L_i(x ω_i, λ)=L_o(r_Μ(x, ω_i). Таким чином, рівняння (2) припускає, що фотони можуть взаємодіяти тільки з поверхнями сцени, але не з простором усередині або навколо них. Іншими словами, поверхні сцени з усіх боків оточені вакуумом.

Алгоритми трасування променів є окремими засобами розв'язання рівняння (2). В роботі [4] зазначено, що за допомогою рівняння (2) можливо змоделювати різні ефекти глобального освітлення, проте деякі менш складні ефекти, наприклад, пряме освітлення без урахування тіней, не можуть бути синтезовані. Якщо шлях від точки на поверхні сцени до джерела освітлення перекритий непрозорими поверхнями, тоді дана точка лежатиме у тіні. З іншого боку, якщо поверхні, що блокують світло, цілком прозорі, тоді точка поверхні не буде затінена, проте самі прозорі поверхні не відображатимуть (не заломлюватимуть) світло, отже, не будуть сприйняті сенсором (помітні спостерігачеві). Щоб підвищити гнучкість моделі (2) автори пропонують використовувати не скалярні, а векторні радіометричні функції, які містять дві скалярні функції, що описують помітне і непомітне освітлення.

4.1.2 Алгоритми трасування променів

В окремому випадку, наприклад, коли візуалізуєма сцена містить лише джерела освітлення (у даному випадку інтегральний оператор у правій частині рівняння (2) пропадає повністю) або під час розрахунку прямого освітлення (поверхні, що випромінюють світло, відомі заздалегідь, отже L_o(r_Μ(x, ω_i) -ω_i, λ)=L_e(r_Μ(x, ω_i) -ω_i, λ) для всіх точок x, що належать поверхні джерел освітлення, для інших поверхонь можна прийняти L_o(r_Μ(x, ω_i) -ω_i, λ)=0 або замінити в області інтегрування S² множиною точок на поверхні джерел освітлення) рівняння (2) можна розв'язати аналітично. У загальному випадку для розв'язання рівняння використовують чисельні методи, які дозволяють знайти частковий розв'язок. Різні алгоритми трасування променів призначені для пошуку часткового розв'язку рівняння (2).

Класичним вважається алгоритм зворотного трасування променів, запропонований Уіттедом Тернером (Whitted Turner) в роботі [5]. Алгоритм полягає у проеціюванні пікселів кінцевого зображення на картинну площину з подальшим трасуванням променя скрізь центр кожного пікселя для визначення відповідного відгуку (інтенсивності) j-го пікселя. Кожен крок трасування променя припускає знаходження найближчого перетину променя з усіма поверхнями сцени з подальшим розрахунком прямого освітлення за локальною моделлю освітлення Фонга і додаванням відображеного й заломленого компонентів. Таким чином, у кожній точці x перетину променя з поверхнею розрахунок моделі глобального освітлення по Уіттеду виглядає наступним чином:

$I\left(x\right) = k_{a}I_{a} + k_{d}\sum_{i=1}^{N}I_{d}I_{l_{i}}\theta_{i}v\left(x, \omega_{i}\right) + k_{r}I_{r} + k_{t}I_{t}$

Позначення, використані у рівнянні (3) мають наступне значення:

I — інтенсивність освітлення;
k — коефіцієнт масштабування інтенсивності освітлення;
N — кількість джерел освітлення;
v(x, ω_i) — функція, що повертає значення 1, якщо промінь (x, ω_i) не перетинає поверхні сцени, й 0 в іншому випадку

У якості індексів використані наступні позначення:

a — імітація непрямого (ambient) освітлення у точці;
d — пряме розсіяне (diffuse) освітлення у точці;
l — джерело освітлення (light source);
r — дзеркальне відображення (reflection);
t — дзеркальне заломлення (transmittance)

Відображений і заломлений компоненти світла розраховуються шляхом пускання променів у відображеному й заломленому напрямках та розв'язання рівняння (3) у кожній наступній точці перетину. Загалом кажучи, для синтезу реалістичного зображення, коефіцієнти відображення і заломлення слід обирати на основі закону Френеля, який встановлює залежність між кутом нахилу променя щодо нормалі поверхні і кількістю відображеної і заломленої світлової енергії.

Наступна анімація демонструє процес вирішення проблеми освітлення за допомогою алгоритму Уіттеда (рис. 1). На рисунку, залежно від використовуваної моделі освітлення, об'єкти позначені символами D (diffuse, розсіяне) і S (specular, дзеркальне), а індексами r і t позначені, відповідно, відображення й заломлення. Джерела освітлення позначені символом L (light). Первинні промені мають зелений колір, тіньові (shadow feelers) — чорний, відображені — синій, заломлені — фіолетовий. На рисунку 2 також відзначені проекції точок перетину тіньових променів з поверхнями сцени (у тривимірному просторі).

Модель поширення світла, реалізована класичним алгоритмом трасування променів
(анімація: кількість кадрів: 10; частота кадрів: 1 кадр / с; кількість циклів повторення: 7; розмір: 25.6 Кб).

Можна помітити, що вторинні розсіяні відображення (і заломлення) за допомогою класичного алгоритму трасування променів не моделюються.

В роботі [3] запропоновано алгоритм трасування шляхів (Path tracing), основу якого складає ідея про те, що найбільший внесок в оцінку енергетичної яскравості вносять первинні і тіньові промені, тобто, промені, що лежать на початку і в кінці шляху між джерелом освітлення і сенсором. Оскільки і класичний алгоритм трасування променів, і його розширений стохастичний варіант, розподілене трасування променів (Distributed / Distribution ray tracing) [6], будують дерево променів, що містить переважно проміжні промені, обчислювальні ресурси витрачаються марно (на розрахунок освітлення, яке, порівняно із первинним, зазвичай незначною мірою впливає на підсумковий результат).

4.1.3 Відображення алгоритмів трасування променів на паралельну архітектуру GPU

В основі архітектури GPU лежить принцип SIMD-обчислень, який передбачає паралельне виконання однієї інструкції багатьма потоковими процесорами, кожний з яких опрацьовує власний елемент вхідного потоку даних. Завдяки високому ступеню паралелізму, а також традиційній орієнтації на використання в графічних застосуваннях, які вимагають швидких обчислень з плаваючою крапкою, сумарна продуктивність GPU (зокрема, за умовою лінійності виконуваного коду) значно перевищує CPU.

Далі наведено графік [7], що відображає порівняльну динаміку зміни продуктивності різних поколінь GPU від Nvidia і архітектур CPU від Intel за останні тринадцять років (рис. 2). На графіку помітне лінійне, а потім майже експоненціальне зростання продуктивності GPU. Навіть без урахування інших важливих факторів, це можна пояснити, порівнявши кількість обчислювальних ядер у GeForce 8800 GTX (575 [8]) і у GeForce GTX 780 Ti (2880 [9]), позначених на графіку.

Порівняння динаміки зростання продуктивності GPU і CPU

Незважаючи на те, що GPU традиційно орієнтовані на використання в графічних застосуваннях (виконання растеризації потоку трикутників), існує багато технік і технологій застосування GPU для вирішення неграфічних завдань, які об'єднані загальною назвою GPGPU (General-purpose computing on GPU). Найпростіші техніки GPGPU можуть полягати, наприклад, у нестандартній інтерпретації значень елементів текстур (матриць), що опрацьовуються за допомогою GPU [10]. Проте такий підхід не дозволяє вийти за межі станартного графічного конвеєру, який накладає багато обмежень на програми, що виконуються на GPU. Наприклад, шейдерні програми (вершинні, піксельні), виконувані для кожного елемента потоку даних, не можуть обмінюватися інформацією.

Дана магістерська робота припускає використання програмно-апаратної GPGPU технології CUDA для прискорення процесу візуалізації методами трасування променів. Варто зазначити, що в контексті CUDA використовується поняття SIMT-обчислень (взагалі кажучи, модель SIMT-обчислень використовується й іншими програмними платформами для паралельного програмування, наприклад, OpenCL), відмінність яких від SIMD на рівні коду полягає в можливості написання коду для окремих ниток як самостійних програм, а не однієї програми для паралельної обробки усього вектора даних. Таким чином, зникає необхідність явно вказувати ширину вектора даних в програмі і вручну контролювати, яка частина вектора у разі розгалуження коду буде оброблятися, а яка ні [7].

З точки зору геометричної оптики, що лежить в основі розглянутих вище алгоритмів трасування променів, фотони — це частинки, які не взаємодіють між собою, тому трасування кожного променя може виконуватися незалежно від інших променів, дозволяючи таким чином розпаралелити процес синтезу зображення. Однак розпаралелювання реалізації алгоритму на рівні одного семплу пікселя є лише одним з багатьох варіантів відображення алгоритму на архітектуру GPU.

Реалізація алгоритмів трасування променів ускладнена великою кількістю чинників, як-то можливе завершення потоків виконання ниток у різний час (наприклад, у випадку, якщо частина променів поглинена або не перетнула жодної поверхні сцени), розгалуження потоків виконання ниток (наприклад, якщо різні промені зіткнулися з поверхнями, що мають різні матеріали). Якщо подібні ситуації трапляються всередині варпа (warp, група ниток, що виконуються паралельно), ефективність виконання паралельної програми різко падає.

У роботі [11] розглянуті способи підвищення ступеня утилізації варпа для першого з перерахованих варіанту розбіжності потоку виконання ниток. Автор порівнює ефективність трьох варіантів реалізації алгоритму стохастичною трасування шляхів.

Перший варіант реалізації. Проста (наївна) реалізація, що припускає опрацювання кожного пікселя окремою ниткою. Сортування активних ниток не виконується, тому додаткові витрати пам'яті на зберігання й опрацювання буферів відсутні.

У другому варіанті реалізації кожна нитка зіставлена одному пікселю зображення, але виконує лише один крок трасування (у тому числі генерацію первинних променів), таким чином ядро запускається багаторазово доти, доки не завершиться трасування всіх шляхів. Утилізація варпа досягається за допомогою трьох буферів, що містять, множину трасованих шляхів, ознаки активності кожного шляху і індекси у буфері трасованих шляхів, відповідні кожній нитці. Кожна нитка після чергового кроку трасування оновлює ознаку активності відповідного шляху, а після завершення виконання всіх ниток, на стороні хоста виконується послідовне заповнення третього зазначений буфер індексами буфера ознак активних шляхів, що відповідають ще активним шляхах. Таким чином, під час наступного запуску ядра, нитки з послідовними індексами будуть обробляти тільки активні шляхи, отже варпи будуть заповнені рівномірно (відповідно до [7], заповнення варпа відбувається послідовно, починаючи з найменшого індексу нитки).

Третій варіант реалізації утилізації варпів передбачає повне трасування кожною ниткою у межах блоку ниток визначеної постійної для всіх ниток кількості шляхів. Така організація обчислень дозволяє уникнути численного запуску ядра. Сортування активних шляхів виконується всередині кожного блоку з використанням наведеного вище алгоритму. Окрім того, враховуючи, що обмін даними виконується всередині блоку, можливо використання швидкої спільно використовуваної пам'яті.

Третій варіант реалізації теоретично повинен працювати швидше за інші, проте саме він продемонстрував найгірші результати (табл. 1). Автор пояснює це тим, що велика кількість задіяних регістрів (64) на одну нитку і спільно використовуваної пам'яті на блок ниток призводять до низької завантаженності варпів нитками через обмеження на загальну кількість доступних одному мультипроцесору регістрів і спільно використовуваної пам'яті.

Загальна продуктивність ядер (у кадрах в секунду), що утилізують варпи у порівнянні зі стандартним ядром (максимальна довжина шляху обмежена вісьмома відображеннями)

Сцена	Варіант реалізації ядра
Сцена	1	2		3
Fairy	3.13	3.54	+13%	1.08	-66%
Moto	2.03	2.29	+13%	0.74	-64%
Troll	3.19	3.63	+14%	1.10	-66%
Dragon	3.61	4.06	+12%	1.21	-66%
Dreamhome	3.42	3.88	+13%	1.23	-64%
Refinery	4.17	4.84	+16%	1.42	-66%

Таким чином, складність виконуваного ядра суттєво впливає на продуктивність реалізації. Зокрема, вище продумонстровано, що причина полягає у недостатній кількості реєстрової і спільно використовуваної пам'яті, доступної кожному потоковому мультипроцесору.

В роботі [12] запропоновано алгоритм обходу прискорюючої структури MBVH з використанням бітового стека, який для поточного вузла на поточному рівні обходу дерева зберігає ознаку обходу його сусідніх вузлів. Незважаючи на більш оптимальне використання пам'яті, що є необхідною умовою досягнення високої продуктивності реалізації, через високий ступінь нелінійності логіки роботи алгоритму, його ефективність у порівнянні зі стековим алгоритмом доволі низька (табл. 2).

Порівняння продуктивності (у мільйонах променів в секунду) стекового і безстекового (із бітовим стеком) алгоритмів обходу бінарного дерева MBVH (з двома AABB у кожному вузлі) на NVIDIA Tesla K20

Сцена	Алгоритм
Сцена	Стековый	Безстековий
Conference	142.7	101.0
Crytek Sponza	93.5	64.2
Fairy	73.1	58.2
Hairball	24.1	18.6
Power Plant	51.7	40.8
San Miguel	33.3	26.3

4.1.4 Методи прискорення трасування променів

Методи прискорення оцінки непрямого освітлення за рахунок фільтрації шумів запропоновані в роботах [13-15]. Завдяки фільтрації вторинного освітлення з дотриманням контурів об'єктів (що в зазначених роботах виконується різними способами), можливе використання меншої кількості семплів вторинного освітлення, завдяки чому скорочується загальний час, що витрачається на синтез візуально прийнятного (розрізнюваного) зображення.

В работе [16] запропонована організація гібридного графічного конвеєра, що комбінує техніки візуалізації, засновані на принципах растеризації і трасування променів (точніше, алгоритму нерекурсивного трасування, ray casting). Цікаво відзначити, що домінуючим елементом у конвеєрі є саме техніки растеризації, за допомогою яких наближено розраховується локальне освітлення (без тіней, використовуючи модель Фонга), тіні (за допомогою карт тіней) і частина непрямого освітлення (розсіяне, за допомогою Light Propagation Volumes), тоді як трасування променів використовується виключно для розрахунку дзеркальних відображень і заломлень. Перевага конвеєра порівняно з повним трасуванням зображення полягає у тому, що трасування променів виконується тільки для помітних частин поверхонь, чий матеріал має відображаючі і/або заломлюючі властивості, що дозволяє уникнути трасування всіх пікселів зображення. З іншого боку, можливі ракурси огляду сцени, за яких такі поверхні будуть займати всю картинну площину, у результаті чого доведеться виконувати трасування всього зображення цілком. Крім того, виникає завдання узгодження результатів роботи кожної техніки візуалізації (наприклад, алгоритм ray casting не здатний розрахувати розсіяне освітлення, тоді як на стадії растеризації воно додається).

4.2 Огляд національних джерел

У роботі Шатовської Т. Б. і Кудлай С. Ю. з харківського національного університету радіоелектроніки [17] розглянуті сучасні GPGPU-технології, а також представлені порівняльні результати оцінки ефективності реалізацій класичного алгоритму трасування променів на CPU і GPU (з використанням технології CUDA). Загальний час, витрачений на візуалізацію сцени однією ниткою на CPU, у 89 разів перевищив час трасування на GPU, підтверджуючи таким чином ефективність останнього варіанта реалізації алгоритму.

Дашкевич А. А. і Анісімов К. В. з національного технічного університету Харківський політехнічний інститут [18] пропонують модифікацію алгоритму radiosity для прискорення обчислення форм-фактора, що масштабує кількість світлової енергії, яка передається від джерела освітлення освітлюваної поверхні в залежності від взаємного розташування і орієнтації поверхонь. Як форм-фактор запропоновано використовувати відношення кількості пікселів у проекції поверхні джерела освітлення на одиничний напівкуб до загальної кількості пікселів в зображенні.

4.3 Огляд локальних джерел

У роботі Серженко А. А. запропоновано спосіб прискорення візуалізації трасуванням променів шляхом зменшення кількості трасованих пікселів [19]. Замість трасування кожного пікселя зображення, трасуються лише чотири крайових пікселя блоку певного розміру, а значення інших пікселів усередині даного блоку отримують за рахунок виконання блокової інтерполяції. У якості базового алгоритму автор використовував класичне трасування променів Уіттеда. Відомою проблемою методів точкової вибірки, до яких відноситься класичне трасування променів, є різноманітні артифакти (аліасінг), які проявляються у місцях різкої зміни освітленості сцени (на межах тіней, відображень, у контрастних текстурах) і виникають через недостатню частоти вибірки. У запропонованому алгоритмі частота вибірки істотно зменшена, отже, ймовірність виникнення аліасинга у будь-якій сцені вище. Використання різних схем вибірки (у тому числі, суперсемплінг) частково вирішить проблему аліасинга тільки для чотирьох крайових пікселів, проте не тільки окремі пікселі, а й весь блок може лежати у місці аномалії функції освітленості, тому лінійна інтерполяція може виявитися занадто грубим наближенням подібної ділянки функції.

Іванова Є. В. розглядає можливість застосування GPU з підтримкою технології CUDA для прискорення алгоритмів трасування променів, а також наводить оцінку перспектив розвитку GPU і CPU [20].

Гуров А. В. виконав аналіз методу прискорення пошуку перетинань променів з поверхнями сцени за допомогою kd-дерева [21].

У дослідженні Каламитри М. В. проаналізовано основні алгоритми трасування променів і їх модифікації [22]. Для синтезу фізично чітких зображень запропоновано використовувати алгоритми Distribution ray tracing, Photon mapping, Bidirectional path tracing і Metropolis light transport. У роботі також розглянуті способи відображення алгоритмів трасування променів на паралельну архітектуру GPU.

Запорожченко І. А. досліджує алгоритм 3DDA обходу регулярної сітки і вплив даної техніки прискорення на швидкість пошуку перетину променя з поверхнями сцени [23]. Множина поверхонь сцени, що візуалізується, містить сфери та куби. У роботі продемонстровано, що за фіксованої кількості сфер, розподіл ефективності техніки прискорення близький до нормального.

5. Висновки

Виконано огляд базових алгоритмів візуалізації віртуальних просторових сцен, що використовують принцип трасування променів. Класичним вважається алгоритм зворотного трасування променів, запропонований у роботі [5]. Для розширення діапазону ефектів, що моделюються класичним алгоритмом, у роботі [6] запропоновано алгоритм Distributed (distribution) ray tracing, а у роботі [3], щоб підвищити швидкість синтезу зображення сцени, запропоновано алгоритм Path tracing.

Проаналізовано модифікації базових алгоритмів, орієнтовані на прискорення синтезу зображень. Фільтрація непрямого освітлення дозволяє швидше синтезувати менш зашумлені зображення. Використання гібридної візуалізації, що комбінує принципи растеризації і трасування променів, дозволяє в більшості випадків скоротити час візуалізації у порівнянні з безпосереднім трасуванням променів.

Розглянуто особливості відображення алгоритмів трасування променів на паралельну архітектуру GPU з прив'язкою до технології CUDA. Основна проблема полягає у нестачі пам'яті, оскільки ступінь паралелізму залежить від обсягу реєстрової і спільно використовуваної пам'яті, зайнятої кожною ниткою.

Подальші дослідження будуть присвячені вирішенню наступних завдань:

Розробка оптимізованого алгоритму трасування променів c поліпшеними часовими характеристиками;
Програмна реалізація оптимізованого алгоритму трасування променів на GPU з використанням технології CUDA, що дозволяє виконувати візуалізацію інтерактивних сцен у режимі реального часу;
Оцінка ефективності реалізації

6. Перелік посилань

A survey of ray tracing acceleration techniques / James Arvo, David Kirk // An introduction to ray tracing. — London, UK: Academic Press Ltd., 1989. — С. 201-262.
Robust Monte Carlo Methods for Light Transport Simulation : / Veach Eric. — Stanford University, 1998.
The Rendering Equation / James T. Kajiya // Proceedings of the 13th Annual Conference on Computer Graphics and Interactive Techniques: SIGGRAPH ’86. — New York, NY, USA: ACM, 1986. — С. 143-150
Retro-rendering with vector-valued light: Producing local illumination from the transport equation / Banks D. C., Beason K. M. // Proceedings of SPIE, the International Society for Optical EngineeringSociety of Photo-Optical Instrumentation Engineers, 2006. — С. 60600C.1-60600C.7
An improved illumination model for shaded display / T. Whitted // ACM SIGGRAPH Computer Graphics. — 1979. — Т. 13, № 2. — С. 343-349
Distributed ray tracing / Cook R. L., T. Porter, L. Carpenter // ACM SIGGRAPH Computer Graphics: Т. 18ACM, 1984. — С. 137-145
CUDA C Programming Guide
GeForce 8800 GTX Specifications [Електронний ресурс] — Режим доступу: http://www.geforce.com/hardware/desktop-gpus/geforce-8800-gtx/specifications
GeForce GTX 780 Ti Specifications [Електронний ресурс] — Режим доступу: http://www.geforce.com/hardware/desktop-gpus/geforce-gtx-780-ti/specifications
Основы работы с технологией CUDA / Боресков А. В., Харламов А. А. — ДМК Пресс, 2010. — 232 с.
Active Thread Compaction for GPU Path Tracing / I. Wald // Proceedings of the ACM SIGGRAPH Symposium on High Performance Graphics: HPG ’11. — New York, NY, USA: ACM, 2011. — С. 51-58
Stackless Multi-BVH Traversal for CPU, MIC and GPU Ray Tracing / Áfra A. T., L. Szirmay-Kalos // Computer Graphics Forum. — 2014. — Vol. 33, № 1. — С. 129-140
Guided Image Filtering for Interactive High-quality Global Illumination / P. Bauszat, M. Eisemann, M. Magnor // Computer Graphics Forum: Т. 30Wiley Online Library, 2011. — С. 1361-1368
Practical Noise Reduction for Progressive Stochastic Ray Tracing with Perceptual Control / K. Schwenk, A. Kuijper, J. Behr, Fellner D. W. // IEEE Computer Graphics and Applications. — 2012. — Т. 32, № 6. — С. 46-55
Ускорение расчёта вторичного освещения с помощью фильтрации в пространстве экрана и уточнения на основе информации о близлежащей геометрии / Груздев А. М., Фролов В. А., Игнатенко А. В., 2012. — С. 269-272
Combining Rasterization and Ray Tracing Techniques to Approximate Global Illumination in Real-Time / J. Cabeleira
Використання технологій загальних обчислень на графічних процесорах для прискорення синтезу тривимірних зображень методом зворотного трасування променів / Кудлай С. Ю., Шатовська Т. Б. // октябрь. — 2012
Геометрическое моделирование процесса освещения / Дашкевич А. А., Анисимов К. В. // Вестник Национального Технического Университета Харьковский Политехнический Институт. Серия: Информатика И Моделирование. — 2013. — № 19 (992).
Разработка ускоренного алгоритма трассировки лучей [Електронний ресурс] / Серженко А. А. — Режим доступу: http://masters.donntu.ru/2010/fknt/serezhenko/diss/index.htm
Анализ, исследование и усовершенствование методов реалистической визуализации трёхмерных моделей объектов и сцен с применением функционального описания [Електронний ресурс] / Иванова Е. В. — Режим доступу: http://masters.donntu.ru/2010/fknt/ivanova/diss/index.htm
Реалистичная стерео-визуализация трёхмерных сцен методом трассировки лучей на специализированных параллельных вычислительных системах [Електронний ресурс] / Гуров А. В. — Режим доступу: http://masters.donntu.ru/2011/fknt/gurov/diss/index.htm
Средства фотореалистичной визуализации и их реализация на параллельных компьютерных системах [Електронний ресурс] / Каламитра М. В. — Режим доступу: http://masters.donntu.ru/2013/fknt/kalamitra/diss/index.htm
Анализ алгоритмов трассировки лучей для реалистичной визуализации трёхмерных сцен и способов уменьшения их вычислительной сложности / Запорожченко И. А., Григорьев М. А., Зори С. А. // ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ И ИЗОБРАЖЕНИЙ. — 2013. — С. 352-357

Порфіров Павло Олександрович

Факультет комп'ютерних наук та технологій

Кафедра комп'ютерної інженерії

Спеціальність: Інженерія програмного забезпечення

Тема магістерської роботи: Підвищення продуктивності синтезу стерео-зображень тривимірних сцен методом трасування променів на паралельних графічних процесорах

Науковий керівник: к.т.н., доц. Зорі Сергій Анатолійович

Реферат за темою випускної роботи