Abstract
Contents
- Introduction
- 1. Investigation of existing formats for floating point numbers
- 2. Postbinary modified formats
- 3. Program model
- 4. Expected results
- Conclusion
- References
Introduction
Question of the validity and accuracy of the calculations becomes increasingly important because, for most calculations, which are currently used in automated processes appearance and accumulation of errors can lead to various kinds of consequences and accidents. Computer systems use two formats for storage numbers – integers and floating point numbers. With integer representation problems usually arise because of the right approach in programming, this format does not cause the accumulation of errors. Fractional numbers are represented in floating point format, and since the numbers converted to the format may contain some error, then the arithmetic operations can accumulate this error and it becomes unacceptably high. In the current literature there are many examples where the accumulation of errors caused disasters.
For example, [11] referred to the disaster involving the use of military equipment (errors in calculating the trajectory of missiles) and in the oil industry (miscalculation of safety design of an oil platform). In [12], the error in the economic sphere, when the accumulation of errors may cause a malfunction of the banking system. In [5] the crashes caused by errors and inaccuracies which were produced by computer calculations are disassembled and analyzed.
In [4, 5] errors of computing with numbers in floating point standard IEEE 754–2008 in problems of a theoretical nature are considered and reasoned.
The aim of this work is to study the disadvantages of the existing format is used, the study developed a modified format and identify their strengths as well as the implementation of the software to work with the new format, which will perform four basic arithmetic operations.
1. Investigation of existing formats for floating point numbers
In computing systems we use IEEE– 754 format for presenting numerical data [10].
This format is a floating point number has two forms:
– Single precision (32 bits). These numbers provide only accurate to 7–8 decimal numbers. They range from 10–308... 10308. In Figure 1 it can be seen that the format consists of the sign (1 bit), the order of (8 bits) and the mantissa (22 bits).
– Double–precision (64–bit). Provide the number to 15 decimal numbers after the decimal point in the range of 10–308 to 10308. Here an order given to 11 bits, and 52 bits of mantissa, as can be seen from Figure 2.
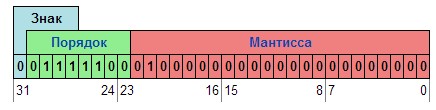
Figure 1.1 – The format of single–precision number [10]

Figure 1.2 – The format of double precision number [10]
Since 2008 there is a quadruple –precision format with 15 bit exponent and 112 bit mantissa.
In [2] the features of this format are analyzed, as well as errors that may result from its use. Also in [4] it is represented one of the most famous "polynomial Rump", the calculation of which due to the nature of formats floating–point single–and double–precision leads to incorrect results.
All this points to the disadvantages associated with using the IEEE 754 format. Therefore, there is need for a new format, which would reduce the error computation and improve its accuracy. So the solution is, the using of postbinary formats, and also their modifications.
2. Postbinary modified formats
.Question the reliability of computing is discussed in several scientific papers and publications [5,8]. Some of them encourage to use interval analysis and arithmetic as a means of excluding rounding errors, but this approach has drawbacks. For storage of interval numbers we have to use IEEE–754 format.
Therefore it makes sense to consider using of a modified format that uses tetralogics and tetracoding which is presented in [3,6,7,9].
Tetralogics is based on the using of 4 states – 1, 0, M, A.
A – set absolute uncertainty (unknown or "true" or "false"), which is expressed by combining sets of "true" and "false"
M – multiplicity, ambiguity (and "true" and "false" at the same time, that can not clearly fix statements), you want to express the intersection of sets of "true" and "false".
Since tetrit acts as a digit of tetracode, then we are able to store multiple and uncertain numeric data, thus realizing the principle of multi–code representation of numerical data.
One of the modifications of postbinary formats is pbinary 128 (256)/32 (64) fp. The overall structure of the data formats for different capacity is shown in Figure 2.1 and Figure 2.2.

Figure 2.1 – Modified format for 128– bit [1]

Figure 2.2 – Modified format for 256– bit [1]
This format allows make one of the functions – performance of "deferred division" when the numerator and denominator are calculated, each of them separately and directly the division is made on the last step of the calculation. This allows you not to lose precision in operations requiring repeated division that lead to the accumulation of unacceptable error.
However, since this is postbinary format, as a result, we obtain an interval.
3. Program model
Analysis of the structure proposed in [3] of modified formats showed that for software implementation of tetracalculations with multi–code representation of data using of a single fractional format (pbinary128/32fp) and double precision (pbinary256/64fp) keeps all the factors of necessity and sufficiency. This format encoding number to field in the numerator and denominator on the principle of common mathematical fractions, however, the numerator and denominator are represented as floating point numbers.
For a software implementation of tetraarithmetics with numbers in formats pbinary128/32fp and pbinary256/64fp was chosen PHP language, which is a scripting language for developing web applications. The advantages are obvious: the computation can be implemented as a Web application that is cross–platform and accessible to users who are connected to the Internet. Language PHP is also chosen due to its close interaction with lots of different database management systems (eg, MySQL).
Tetracomputing organization is such that its software implementation requires a numerous string–numeric conversions, with a subsequent calculations on integers with arbitrary precision.
Therefore, we considered library implementing a "long arithmetic" standard library in C# and JavaScript, as well as an external library GMP (GNU Multi–Precision Library) for C# and PHP. Researches, the results of which are shown in Fig. 3.1 showed that a bunch of PHP + GMP is most optimal, because it is the fastest.

Figure 3.1 – Results of research performance
(1 – cyclical exponentiation 2 – single exponentiation 3 – addition is "long" number 4 – a translation of a string in "long" number 5 – translate "long" numbers in a row ; 6 – subtraction "long" numbers)
Software implementation of the calculator assumes development of the algorithm, which is presented in Fig. 3.2 This algorithm provides a common sequence of basic operations associated with data conversion and tetraarithmetics.
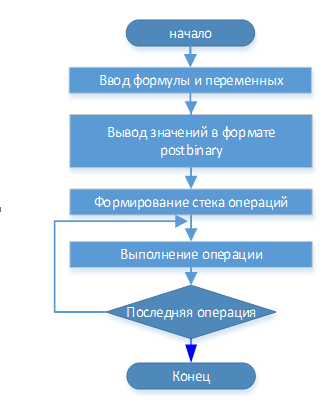
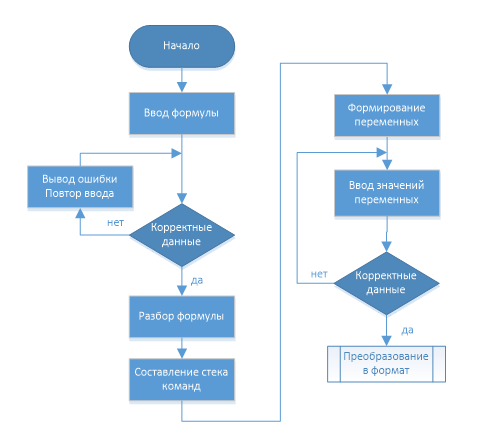
Figure 3.2 – Block diagram of the proposed calculator
(left – general view, to the right – the first part of the work)
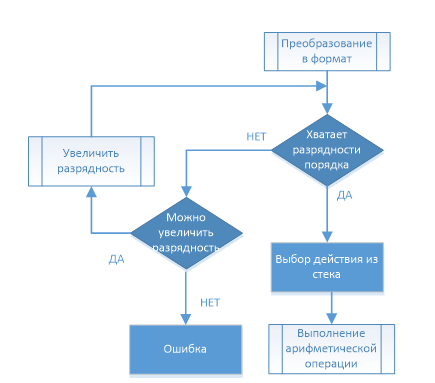

Figure 3.2 – Block diagram of the proposed calculator
(left – the continuation of the work on the right – the final part)
As already mentioned, the majority of computing devices and systems used to represent the numbers in format IEEE754 –2008. This format consists of a field mark, order and the mantissa. Postbinary formats preserves the overall structure, but some bits are reserved for modifier field. The program performs the conversion of numbers to postbinary fractional format and allows you to perform simple arithmetic. The program interface is shown in Figure 3.3. It is a text box for entering a formula. You can enter variables and numbers in a normal and exponential form. By pressing the "Enter formula" opens next part of the interface, shown in Figure 3.4
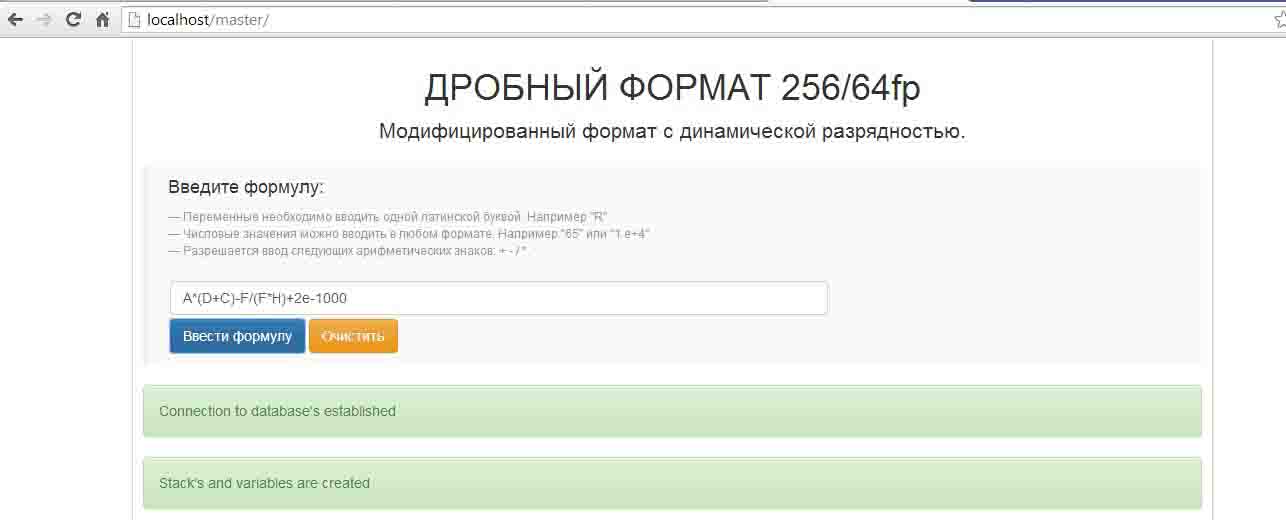
Figure 3.3 – Basic interface
This interface unit is a field for input variables. Since format is fractional, the number of input fields for each variable is two. One for the numerator, the second – for the denominator. The number of pairs is equal to the number of variables in the formula. After entering the values goes the stage of conversion. Numbers are converted to the format and are also visualized. This can be seen from Figure 3.5.

Figure 3.4 – Interface for input variables

Figure 3.5 – Visualization format
The next step is to create a stack of commands. Variables, as well as the stack of commands stored in the database. The stack is presented in the form of operands and the internal operation. All operations are performed in order from a lower to a higher level, so that the result of previous operations may be used to follow.

Figure 3.6 – Stack operations
Further we implement arithmetic operations directly. Result of their computing will also be visualized, step by step with the mapping errors, if such can occur.
Step by step operation with the software product is displayed in Figure 3.7.

Figure 3.7 – Step by step operation with the program (animation: 10 frames, 5 cycles of repeating, 138 kilobytes)
The animation shows what is needed to calculate the formula – from input to a result. Moreover, there are explanations of animation for better understanding of the program.
4. Expected results
The final stage is to develop a full–fledged software product that will perform basic arithmetic operations (addition, subtraction, multiplication, division) with numbers represented in a modified fractional format. The program will be implemented using PHP/MySQL, thus providing cross–platform. All calculations are performed on the server side, which allows the user not to think about the need for a more powerful computer.
Program will enter a formula that can be used as variables and numbers in exponential form. All numbers will be converted to the corresponding modified format, and then using the developed algorithms will make calculations. Results will be presented in the form of a fraction, and in the appropriate format. Moreover, the program will dynamically change the capacity. Thus, the numbers of an appropriate capacity bit will be stored in it, if the conversion to format or the result of operation cannot be placed in a bit net, there will be used a larger capacity. This will be one of the features of this software.
Conclusions
Within this work are described the existing formats of representation of numbers, as well as newer modified formats for storing floating–point numbers. Also implemented a software application that allows you to work with numbers in a modified format.
In writing this essay, master's work is not finished. Final completion is scheduled for December 2014. Work can be obtained from the author or the head after her delivery.
List of sources
1. Аноприенко А.Я., Иваница С.В., Кулибаба С.В. Особенности представления постбинарных вещественных чисел в контексте интервальных вычислений и развития аппаратного обеспечения средств компьютерного моделирования // Моделирование и компьютерная графика / Материалы IV международной научно—технической конференции – 5—8 октября 2011 г. Донецк, ДонНТУ. – 2011. С. 13—19.
2. Бесплатные программы SoftElectro. Программа IEEE754 — конвертор чисел формата IEEE 754 c абсолютной точностью представления результата. Electronic resource. Access mode: http://www.softelectro.ru/program.html.
3. Аноприенко А.Я., Иваница С.В. Постбинарный компьютинг и интервальные вычисления в контексте кодо—логической эволюции. — Донецк, ДонНТУ, УНИТЕХ, 2011. — 244 с.
4. Loh E., Walster G. Rump’s Example Revisited // Reliable Computing 8: 2002, p. 245–248.
5. Петров Ю.П. Обеспечение надежности и достоверности компьютерных расчетов. — СПб: БХВ—Петербург, 2008. — 160 с.
6. Аноприенко А.Я., Иваница С.В. Особенности постбинарного кодирования на примере интервального представления результатов вычислений по формуле Бэйли—Боруэйна—Плаффа // Научные труды Донецкого национального технического университета. Серия: «Информатика, кибернетика и вычислительная техника» (ИКВТ—2010). Выпуск 11 (164). – Донецк: ДонНТУ, 2010. С. 19—23.
7. Аноприенко А.Я., Иваница С.В. Интервальные вычисления и перспективы их развития в контексте кодо—логической эволюции // Научные труды Донецкого национального технического университета. Серия «Проблемы моделирования и автоматизации проектирования динамических систем» (МАП—2010). Выпуск 8 (168): Донецк: ДонНТУ, 2010. С. 150–160.
8. Moore R.E. Interval analysis. Eiiglewood Cliffs / R.E. Moore — N.J.:Prentic—e—llall, 1966.
9. Иваница С.В., Аноприенко А.Я. Особенности реализации операций тетралогики // Научные труды Донецкого национального технического университета. Серия: «Информатика, кибернетика и вычислительная техника» (ИКВТ—2011). Выпуск 13 (185). – Донецк: ДонНТУ, 2011. С. 134—140.
10. IEEE Standard for Floating—Point Arithmetic (IEEE 754). Electronic resource. Access mode: http://en.wikipedia.org/wiki/IEEE_754—2008
11. Douglas N. Arnold Some disasters attributable to bad numerical computing / Electronic resource. Access mode: http://www.ima.umn.edu/~arnold/disasters — Загл. с экрана.
12. Brisebarre N. Floating—Point Arithmetic / F. Dinechin, C. Jeannerod, V. Lefevre, G. Melquiond, J. Muller, N. Revol, D. Stehle, S. Torres — Laboratoire LIP, Projet Arenaire CNRS, INRIA, Ecole Normale Superieure de Lyon. — France, 2009 — 16 р.
