Реферат по теме выпускной работы
Содержание
- Введение
- 1. Исследование существующих форматов представления чисел с плавающей запятой
- 2. Постбинарные модифицированные форматы
- 3. Программная модель
- 4. Ожидаемые результаты
- Выводы
- Список источников
Введение
Вопрос достоверности и точности вычислений становится все более актуальным, поскольку для большинства расчетов, которые используются сегодня в автоматизированных технологических процессах появление и накопление погрешностей может привести к различного рода последствиям и стать причиной катастроф. В вычислительных системах используются два формата хранения чисел – целые и числа с плавающей запятой. С целочисленным представлением проблем обычно не возникает, поскольку при правильном подходе при программировании, данный формат не является причиной накопления погрешностей. Дробные же числа представляются в формате с плавающей запятой, и поскольку числа при переводе в формат могут содержать некоторую погрешность, то при выполнении арифметических операций, данная погрешность может накапливаться и становится недопустимо высокой. В современной научной литературе есть немало примеров, где накопление погрешности стало причиной катастроф.
Так, например, в [11] упоминаются катастрофы, связанные с использованием военной техники (ошибки в расчете траектории полета ракет) и в нефтедобывающей промышленности (неверный расчет запаса прочности конструкции нефтяной платформы). В работе [12] приведены ошибки в экономической сфере, когда накопление погрешности может вызвать сбой в работе банковской системы. В книге [5] разобраны и проанализированы авиакатастрофы, вызванные породившими неточности и ошибки компьютерными вычислениями.
В [4, 5] рассмотрены и аргументированы ошибки компьютерных вычислений с числами в формате с плавающей запятой стандарта IEEE 754-2008 в задачах теоретического характера.
Поэтому целью данной работы является исследование недостатков существующих использующихся форматов, исследование разработанных модифицированных форматов и выявление их преимуществ, а также реализация программного обеспечения для работы с новыми форматами, которое позволит выполнять 4 основные арифметические операции.
1. Исследование существующих форматов представления чисел с плавающей запятой
В вычислительных системах используется формат IEEE-754 для представления числовых данных [10].
Данный формат представляет числа с плавающей запятой в двух видах:
— Одинарной точности (32 бита). Такие числа обеспечивают точность лишь до 7-8 десятичных чисел. Их диапазон от 10-308…10308. На рисунке 1 можно увидеть, что формат состоит из знаковой части (1 бит), порядка (8 бит) и мантиссы (22 разряда).
— Двойной точности (64 бита). Числа обеспечивают до 15 десятичных чисел после запятой в диапазоне от 10-308 до 10308. Здесь на порядок отведено 11 бит, а на мантиссу 52 бита, в чем можно убедиться из рисунка 2.
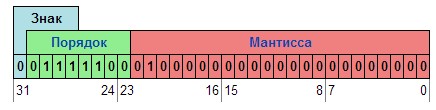
Рисунок 1.1 – Формат числа с одинарной точностью [10]

Рисунок 1.2 – Формат числа с двойной точностью [10]
С 2008 года появился формат четверной точности с 15 битной экспонентой и 112 битной мантиссой.
В [2] проанализированы особенности данного формата, а также ошибки, к которым может привести его использование. Также в работе [4] представлен один из наиболее известных «полином Румпа», вычисление которого из-за особенностей форматов чисел с плавающей запятой одинарной и двойной точности приводит к неверному результату.
Все это указывает на недостатки, связанные с использованием формата IEEE 754. В связи с этим, появляется необходимость в новом формате, который позволит уменьшить погрешность вычислений и повысить их точность. Таким решением есть использование постбинарных форматов, а в частности и их модификаций.
2. Постбинарные модифицированные форматы.
Вопрос достоверности компьютерных вычислений рассматривался в ряде научных работ и публикаций [5,8]. В некоторых из них предлагается использовать интервальный анализ и арифметику как средства учета ошибок округления, однако такой подход не лишен недостатков. Для хранения интервальных чисел снова приходится прибегать к формату IEEE 754.
Именно поэтому имеет смысл рассмотреть модифицированный формат с использованием тетралогики и тетракодирования, который представлен в работах [3,6,7,9].
Тетралогика основывается на использовании не 2х состояний 0 и 1, а на 4-х – 1, 0, М, А.
А – множество абсолютной неопределенности (неизвестно, или «истина» или «ложь»), которая выражена объединением множеств «истина» и «ложь»
М – множественность, многозначность (и «истина» и «ложь» одновременно, т.е. невозможна однозначная фиксация высказывания), которую нужно выразить пересечением множеств «истина» и «ложь».
Так как в качестве разряда тетракода выступает тетрит, то мы получаем возможность хранить множественные и неопределенные числовые данные, таким образом реализовывая принцип многокодового представления числовых данных.
Одна из модификаций постбинарных форматов pbinary 128(256)/32(64)fp. Общая структура данных форматов для различной разрядности представлена на рисунке 2.1 и рисунке 2.2.

Рисунок 2.1 – Модифицированный формат 128-битной разрядности [1]

Рисунок 2.2 — Модифицированный формат 256-битной разрядности [1]
Данный формат позволяет реализовать одну из функций — выполнение «отложенного деления», когда вычисляются числитель и знаменатель, причем каждый из них отдельно, а непосредственно деление производится на последнем шаге вычисления. Это позволяет не терять точности при операциях, требующих многократного деления и приводящие к накоплению недопустимой погрешности.
Однако, поскольку это постбинарный формат, то в результате вычисления мы получаем интервал.
3. Программная модель
Анализ структуры предложенных в [3] модифицированных форматов показал, что для программной реализации тетравычислений с обеспечением многокодового представления данных использование дробного формата одинарной (pbinary128/32fp) и двойной точности (pbinary256/64fp) отвечает всем факторам необходимости и достаточности. Это формат кодирующий число в поля числителя и знаменателя по принципу обыкновенной математической дроби, однако и числитель и знаменатель представлены как числа с плавающей запятой.
Для программной реализации тетраарифметики с числами в форматах pbinary128/32fp и pbinary256/64fp был выбран язык PHP, являющийся скриптовым языком для разработки веб—приложений. Преимущества такого выбора очевидны: вычисления могут быть реализованы в виде веб—приложения, которое будет кроссплатформенным и доступным для пользователей, подключенных к сети Интернет. Выбор языка PHP также обусловлен его тесным взаимодействием с большим количеством различных систем управления базами данных (например, MySQL).
Организация тетравычислений такова, что ее программная реализация требует обеспечение многочисленных взаимообратных строково—числовых преобразований с последующей организацией вычислений над целыми числами с произвольной точностью.
Поэтому в рассмотрение попали библиотеки, реализующие «длинную арифметику»: стандартные библиотеки языков C# и JavaScript, а также внешняя библиотека GMP (GNU Multi—Precision Library) для языков C# и PHP. Проведенные исследования, результаты которых приведены на рис. 3.1, показали, что связка PHP + GMP оптимальна, поскольку является самой быстрой.

Рисунок 3.1 – Результаты исследования быстродействия
(1 – цикличное возведение в степень; 2 – единичное возведение в степень; 3 – операция сложения «длинных» чисел; 4 – перевод из строки в «длинное» число; 5
– перевод «длинного» числа в строку;
6 – операция вычитания «длинных» чисел)
Программная реализация вычислителя предполагает разработку алгоритма, который представлен на рис. 3.2 Данный алгоритм предоставляет общую последовательность выполнения основных операций, связанных с преобразованием данных и тетраарифметикой.
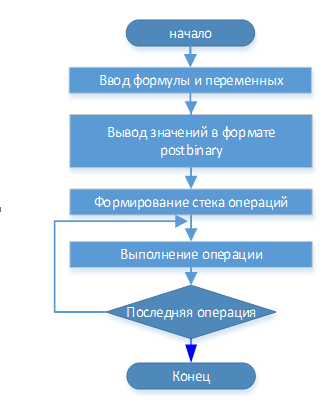
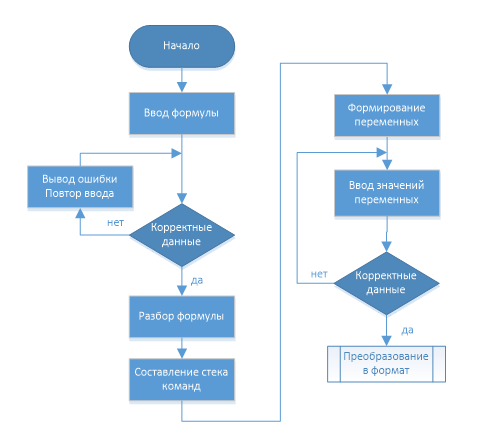
Рисунок 3.2 – Блок—схема работы предложенного вычислителя
(слева – общий вид, справа – первая часть работы)
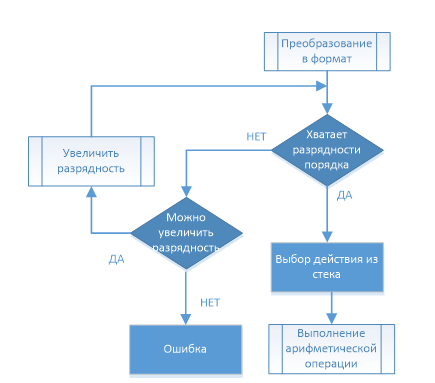

Рисунок 3.2 – Блок—схема работы предложенного вычислителя
(слева – продолжение работы, справа – завершающая часть)
Как уже было сказано, большинство вычислительных устройств и систем используют для представления чисел формат IEEE 754-2008. Данный формат состоит из поля знака, мантиссы и порядка. Постбинарный формат сохраняет общую структуру, однако несколько бит отведены под поле модификатора. Программа реализует преобразование чисел в постбинарный дробный формат и позволяет выполнять простейшие арифметические операции. Интерфейс программы представлен на рисунке 3.3. Он представляет собой текстовое поле для ввода формулы. Можно вводить как переменные, так и числа в обычной и экспоненциальной форме. По нажатию кнопки «Ввести формулу» открывается следующая часть интерфейса, представленная на рисунке 3.4
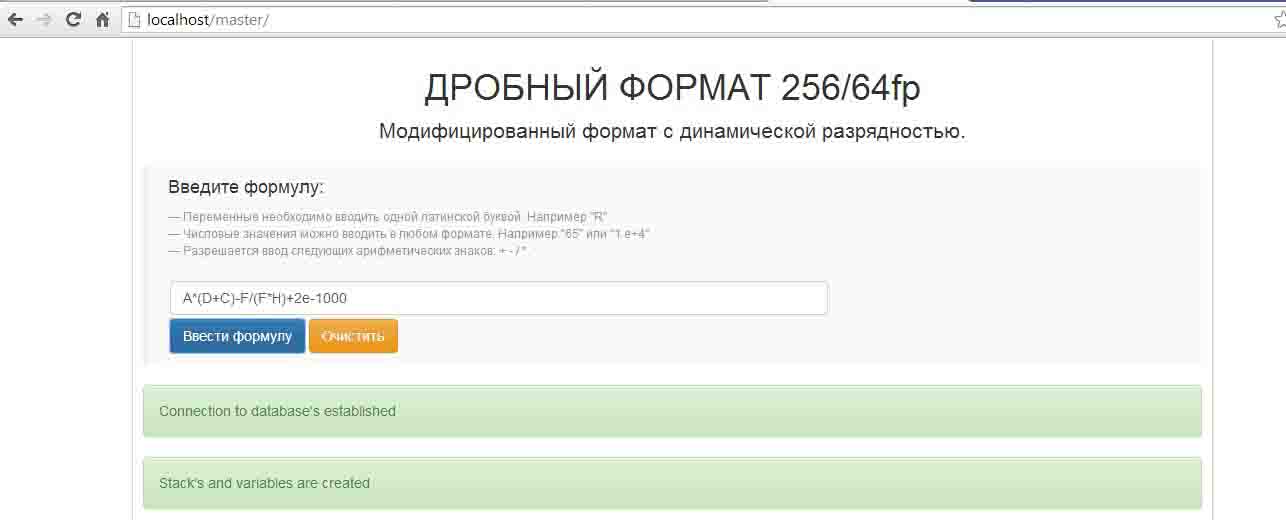
Рисунок 3.3 – Начальный интерфейс программы
Данный блок интерфейса представляет собой поля для ввода значений переменных. Поскольку формат дробный, то полей ввода для каждой переменной два. Одно для числителя, второе – для знаменателя. Количество пар равно количеству переменных в формуле. После ввода значений идет этап преобразования в формат. Числа, преобразованные в формат также визуализируются. Это можно увидеть из рисунка 3.5.

Рисунок 3.4 – Интерфейс для ввода переменных

Рисунок 3.5 – Визуализация формата
Следующим этапом является формирование стека выполняемых команд. Переменные, как и стек выполняемых команд хранятся в базе данных. Стек представлен в виде операнда и внутренней операции. Все операции выполняются по порядку с нижнего уровня до высшего, таким образом результат предыдущих операций может быть использован для последующих.

Рисунок 3.6 – Стек операций
Далее выполняется реализация непосредственно арифметических операций. Результат их выполнения также будет визуализирован, пошагово с отображением ошибок, если такое могут возникнуть.
Пошаговая работа с программным продуктом отображена на рисунке 3.7.

Рисунок 3.7 – Пошаговая работа с программой (анимация: 20 кадров, 5 циклов повторения, 138 килобайт)
На анимации видно, что необходимо сделать для расчета формулы – от ввода данных до получения результата. Более того, на анимации присутствуют пояснения для лучшего понимания работы программы.
4. Ожидаемые результаты
Конечным этапом работы является разработка полноценного программного продукта, который позволит выполнять элементарные арифметические действия (сложение, вычитание, деление, умножение) с числами, представленными в модифицированном дробном формате. Программа будет реализована с использованием PHP/MySQL, обеспечивая таким образом кроссплатформенность. Все расчеты выполняют на серверной стороне, что позволяет пользователю не задумываться о необходимости использования более мощного компьютера.
Программа позволит вводить формулу, в которой могут быть использованы как переменные, так и числа в экспоненциальной форме. Все числа будут переведены в соответствующий модифицированный формат, а затем при помощи разработанных алгоритмов будут произведены расчеты. Результаты будут представлены как в виде дроби, так и в соответствующем формате. Более того, программа будет динамически изменять разрядность. Таким образом, числа которые помещаются в формат меньшей разрядности будут сохранены в нем, если при переводе в формат или после выполнения операции число не помещается в данную разрядную сетку, то будет произведен переход к большей разрядности. Это будет одной из особенностей данного программного продукта.
Выводы
В рамках данной работы описаны существующие форматы представления чисел, а также более новые модифицированные форматы для хранения чисел с плавающей запятой. Также реализовано программное приложение, позволяющее работать с числами в модифицированном формате. При написании данного реферата, магистерская работа не закончена. Окончательное завершение планируется к декабрю 2014 года. Работу можно получить у автора или руководителя после ее сдачи.
Список источников
1. Аноприенко А.Я., Иваница С.В., Кулибаба С.В. Особенности представления постбинарных вещественных чисел в контексте интервальных вычислений и развития аппаратного обеспечения средств компьютерного моделирования // Моделирование и компьютерная графика / Материалы IV международной научно—технической конференции – 5—8 октября 2011 г. Донецк, ДонНТУ. – 2011. С. 13—19.
2. Бесплатные программы SoftElectro. Программа IEEE754 — конвертор чисел формата IEEE 754 c абсолютной точностью представления результата. Электронный ресурс. Режим доступа: http://www.softelectro.ru/program.html.
3. Аноприенко А.Я., Иваница С.В. Постбинарный компьютинг и интервальные вычисления в контексте кодо—логической эволюции. — Донецк, ДонНТУ, УНИТЕХ, 2011. — 244 с.
4. Loh E., Walster G. Rump’s Example Revisited // Reliable Computing 8: 2002, p. 245–248.
5. Петров Ю.П. Обеспечение надежности и достоверности компьютерных расчетов. — СПб: БХВ—Петербург, 2008. — 160 с.
6. Аноприенко А.Я., Иваница С.В. Особенности постбинарного кодирования на примере интервального представления результатов вычислений по формуле Бэйли—Боруэйна—Плаффа // Научные труды Донецкого национального технического университета. Серия: «Информатика, кибернетика и вычислительная техника» (ИКВТ—2010). Выпуск 11 (164). – Донецк: ДонНТУ, 2010. С. 19—23.
7. Аноприенко А.Я., Иваница С.В. Интервальные вычисления и перспективы их развития в контексте кодо—логической эволюции // Научные труды Донецкого национального технического университета. Серия «Проблемы моделирования и автоматизации проектирования динамических систем» (МАП—2010). Выпуск 8 (168): Донецк: ДонНТУ, 2010. С. 150–160.
8. Moore R.E. Interval analysis. Eiiglewood Cliffs / R.E. Moore — N.J.:Prentic—e—llall, 1966.
9. Иваница С.В., Аноприенко А.Я. Особенности реализации операций тетралогики // Научные труды Донецкого национального технического университета. Серия: «Информатика, кибернетика и вычислительная техника» (ИКВТ—2011). Выпуск 13 (185). – Донецк: ДонНТУ, 2011. С. 134—140.
10. IEEE Standard for Floating—Point Arithmetic (IEEE 754). Электронный ресурс. Режим доступа: http://en.wikipedia.org/wiki/IEEE_754—2008
11. Douglas N. Arnold Some disasters attributable to bad numerical computing / Электронный ресурс. Режим доступа: http://www.ima.umn.edu/~arnold/disasters — Загл. с экрана.
12. Brisebarre N. Floating—Point Arithmetic / F. Dinechin, C. Jeannerod, V. Lefevre, G. Melquiond, J. Muller, N. Revol, D. Stehle, S. Torres — Laboratoire LIP, Projet Arenaire CNRS, INRIA, Ecole Normale Superieure de Lyon. — France, 2009 — 16 р.
