Реферат за темою випускної роботи
Зміст
- Вступ
- 1. Дослідження існуючих форматів представлення чисел з плаваючою комою
- 2. Постбінарні модифіковані формати.
- 3. Програмна модель
- 4. Очікувані результати
- Висновки
- Перелік посилань
Вступ
Питання достовірності і точності обчислень стає все більш актуальним, оскільки для більшості розрахунків, які використовуються сьогодні в автоматизованих технологічних процесах поява і накопичення похибок може привести до різного роду наслідків і стати причиною катастроф. В обчислювальних системах використовуються два формати зберігання чисел–цілі і числа з плаваючою комою. З поданням цілих чисел проблем зазвичай не виникає, оскільки при правильному підході при програмуванні, даний формат не є причиною накопичення похибок. Дробові ж числа представляються у форматі з плаваючою комою, і оскільки числа при перекладі у формат можуть містити деяку похибку, то при виконанні арифметичних операцій, дана похибка може накопичуватися і стає неприпустимо високою. У сучасній науковій літературі є чимало прикладів, де накопичення похибки стало причиною катастроф.
Так, наприклад, в [11] згадуються катастрофи, пов'язані з використанням військової техніки (помилки в розрахунку траєкторії польоту ракет) і в нафтовидобувній промисловості (невірний розрахунок запасу міцності конструкції нафтової платформи). В роботі [12] наведені помилки в економічній сфері, коли накопичення похибки може викликати збій в роботі банківської системи. У книзі [5] розібрані і проаналізовані авіакатастрофи, викликані комп'ютерними обчисленнями, що призвели до появи неточності і помилок.
В [4, 5] розглянуті і аргументовані помилки комп'ютерних обчислень з числами у форматі з плаваючою комою стандарту IEEE 754-2008 в задачах теоретичного характеру.
Тому метою даної роботи є дослідження недоліків існуючих використовуваних форматів, дослідження розроблених модифікованих форматів і виявлення їх переваг, а також реалізація програмного забезпечення для роботи з новими форматами, яке дозволить виконувати 4 основні арифметичні операції.
1. Дослідження існуючих форматів представлення чисел з плаваючою комою
В обчислювальних системах використовується формат IEEE-754 для представлення числових даних [10].
Даний формат представляє числа з плаваючою комою в двох видах:
–Одинарної точності (32 біта). Такі числа забезпечують точність лише до 7-8 десяткових чисел. Їх діапазон від 10–308... 10308. На рисунку 1 можна побачити, що формат складається зі знакової частини (1 біт), порядку (8 біт) і мантиси (22 розряду).
–Подвійний точності (64 біта). Числа забезпечують до 15 десяткових чисел після коми в діапазоні від 10–308 до 10308. Тут на порядок відведено 11 біт, а на мантису 52 біта, у чому можна переконатися з малюнка 2.
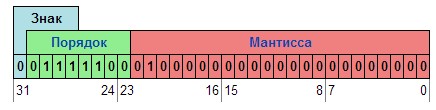
Рисунок 1.1–Формат числа з одинарною точністю [10]

Рисунок 1.2–Формат числа з подвійною точністю [10]
З 2008 року з'явився формат четверний точності з 15 бітною експонентою і 112 бітною мантисою.
В [2] проаналізовано особливості даного формату, а також помилки, до яких може привести його використання. Також в роботі [4] представлений один з найбільш відомих "поліном Румпа", обчислення якого через особливості форматів чисел з плаваючою комою одинарної і подвійної точності призводить до невірного результату.
Все це вказує на недоліки, пов'язані з використанням формату IEEE–754. У зв'язку з цим, з'являється необхідність в новому форматі, який дозволить зменшити похибку обчислень і підвищити їх точність. Таким рішенням є використання постбінарних форматів, а зокрема і їх модифікацій.
2. Постбінарні модифіковані формати.
Питання достовірності комп'ютерних обчислень розглядалося в ряді наукових робіт і публікацій [5,8]. У деяких з них пропонується використовувати інтервальний аналіз і арифметику як засіб обліку помилок округлення, однак такий підхід не позбавлений недоліків. Для зберігання інтервальних чисел знову доводиться вдаватися до формату IEEE-754.
Саме тому є сенс розглянути модифікований формат з використанням тетралогіки і тетракодування, який представлений в роботах [3,6,7,9].
Тетралогіка ґрунтується на використанні не 2х станів 0 та 1, а на 4-х–1, 0, М, А.
А–безліч абсолютної невизначеності (невідомо, чи "істина" або "брехня"), яка виражена об'єднанням множин "істина" і "брехня"
М–множинність, багатозначність (і "істина" і "брехня" одночасно, тобто неможлива однозначна фіксація висловлювання), яку потрібно висловити перетинанням множин "істина" і "брехня".
Так як в якості розряду тетракода виступає тетріт, то ми отримуємо можливість зберігати множинні і невизначені числові дані, таким чином реалізовуючи принцип багатокодового представлення числових даних.
Одна з модифікацій постбінарних форматів pbinary 128(256)/32(64) fp. Загальна структура даних форматів для різної розрядності представлена на рисунку 2.1 і рисунку 2.2.

Рисунок 2.1–Модифікований формат 128–бітної розрядності [1]

Рисунок 2.2–Модифікований формат 256–бітної розрядності [1]
Даний формат дозволяє реалізувати одну з функцій–виконання "відкладеного ділення", коли обчислюються чисельник і знаменник, причому кожен з них окремо, а безпосередньо поділ проводиться на останньому кроці обчислення. Це дозволяє не втрачати точності при операціях, що вимагають багаторазового поділу і призводять до накопичення неприпустимої похибки.
Однак, оскільки це постбінарний формат, то в результаті обчислення ми отримуємо інтервал.
3. Програмна модель
Аналіз структури запропонованих в [3] модифікованих форматів показав, що для програмної реалізації тетраобчислень із забезпеченням багатокодового представлення даних використання дрібного формату одинарної (pbinary128/32fp) і подвійної точності (pbinary256/64fp) відповідає всім факторам необхідності і достатності. Це формат кодує число в поля чисельника і знаменника за принципом звичайної математичної дробу, однак і чисельник і знаменник представлені як числа з плаваючою комою.
Для програмної реалізації тетраарифметики з числами у форматах pbinary128/32fp і pbinary256/64fp була вибрана мова PHP, яка є скриптовою мовою для розробки веб–додатків. Переваги такого вибору очевидні: обчислення можуть бути реалізовані у вигляді веб–додатку, який буде кросплатформеним і доступним для користувачів, підключених до мережі Інтернет. Вибір мови PHP також обумовлений його тісною взаємодією з великою кількістю різних систем управління базами даних (наприклад, MySQL).
Організація тетраобчислень така, що її програмна реалізація вимагає забезпечення численних взаємо–зворотних строково–числових перетворень з подальшою організацією обчислень над цілими числами з довільною точністю.
Тому в розгляд потрапили бібліотеки, реалізують "довгу арифметику" : стандартні бібліотеки мов C# і JavaScript, а також зовнішня бібліотека GMP (GNU Multi–Precision Library) для мов C# і PHP. Проведені дослідження, результати яких наведені на рис. 3.1, показали, що зв'язка PHP + GMP оптимальна, оскільки є найшвидшою.

Рисунок 3.1–Результати дослідження швидкодії
(1–циклічне зведення в ступінь, 2–одиничне зведення в ступінь, 3–операція додавання "довгих" чисел; 4–переклад з рядка в "довге" число; 5–переклад " довгого" числа в рядок; 6–операція віднімання "довгих" чисел)
Програмна реалізація обчислювача передбачає розробку алгоритму, який представлений на рис. 3.2 Даний алгоритм надає загальну послідовність виконання основних операцій, пов'язаних з перетворенням даних і тетраарифметикою.
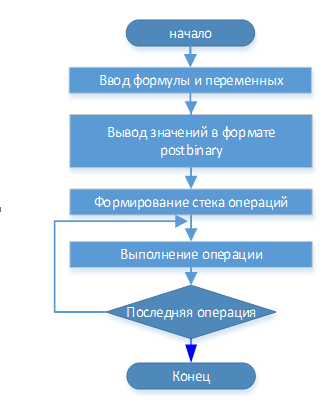
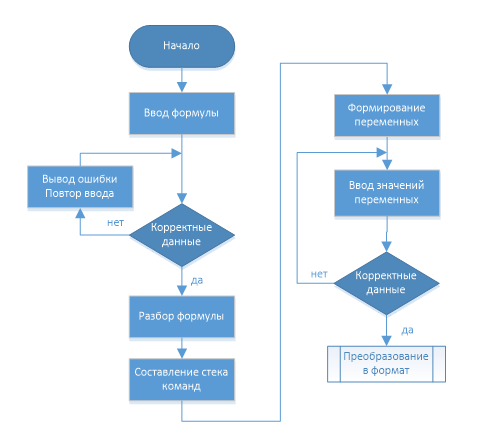
Рисунок 3.2–Блок–схема роботи запропонованого обчислювача
(зліва–загальний вигляд, справа–перша частина роботи)
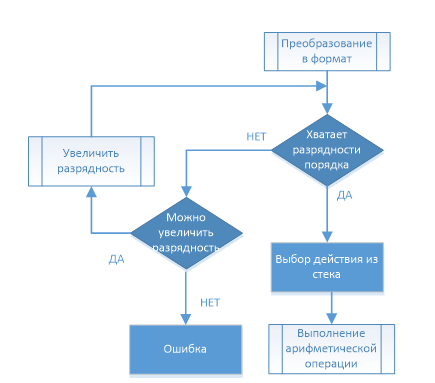

Рисунок 3.2–Блок–схема роботи запропонованого обчислювача
(ліворуч–продовження роботи, справа–завершальна частина)
Як вже було сказано, більшість обчислювальних пристроїв і систем використовують для подання чисел формат IEEE754–2008. Даний формат складається з поля знака, мантиси і порядку. Постбінарний формат зберігає загальну структуру, однак кілька біт відведені під поле модифікатора. Програма реалізує перетворення чисел в постбінарний дробовий формат і дозволяє виконувати найпростіші арифметичні операції. Інтерфейс програми представлений на рисунку 3.3. Він являє собою текстове поле для введення формули. Можна вводити як змінні, так і числа у звичайній і експоненційній формі. По натисканні кнопки "Ввести формулу" відкривається наступна частина інтерфейсу, представлена на рисунку 3.4
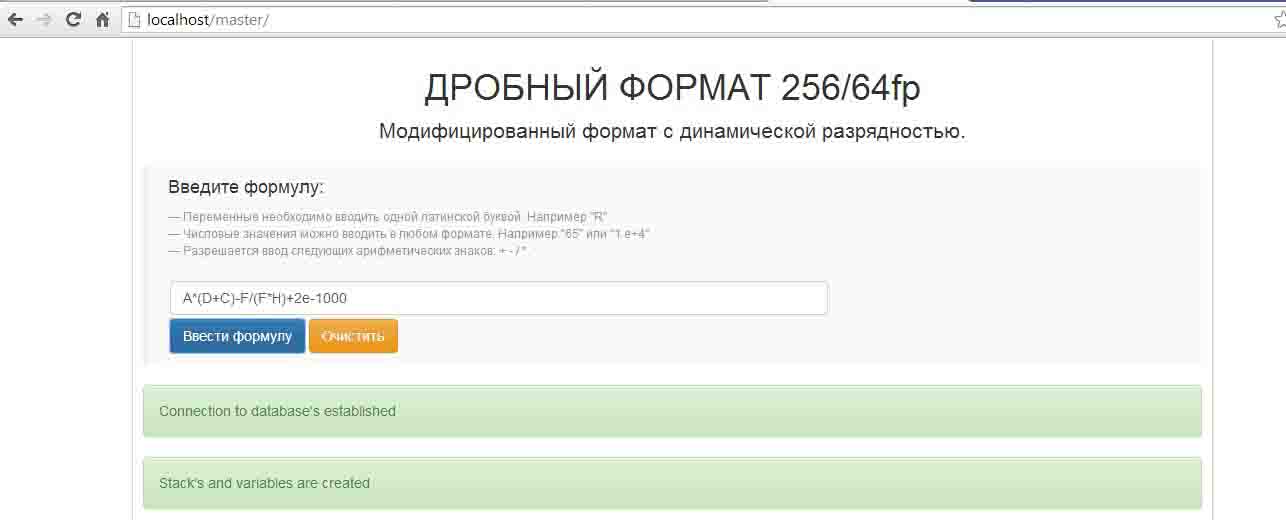
Рисунок 3.3–Початковий інтерфейс програми
Даний блок інтерфейсу являє собою поля для введення значень змінних. Оскільки формат дробовий, то полів введення для кожної змінної два. Одне для чисельника, друге–для знаменника. Кількість пар дорівнює кількості змінних у формулі. Після введення значень йде етап перетворення в формат. Числа, перетворені у формат також візуалізуються. Це можна побачити з малюнка 3.5.

Рисунок 3.4–Інтерфейс для введення змінних

Рисунок 3.5–Візуалізація формату
Наступним етапом є формування стека виконуваних команд. Змінні, як і стек виконуваних команд зберігаються в базі даних. Стек представлений у вигляді операнда і внутрішньої операції. Всі операції виконуються по порядку з нижнього рівня до вищого, таким чином результат попередніх операцій може бути використаний для наступних.

Рисунок 3.6–Стек операцій
Далі виконується реалізація безпосередньо арифметичних операцій. Результат їх виконання також буде візуалізований, покроково з відображенням помилок, якщо такі виникнуть.
Покрокова робота з програмним продуктом відображена на рисунку 3.7.

Рисунок 3.7 – Покрокова робота з програмою (анімація: 20 кадрів, 5 циклів повторення, 138 кілобайт).
На анімації видно, що необхідно зробити для розрахунку формули–від введення даних до отримання результату. Більш того, на анімації присутні пояснення для кращого розуміння роботи програми.
4. Очікувані результати
Кінцевим етапом роботи є розробка повноцінного програмного продукту, який дозволить виконувати елементарні арифметичні дії (додавання, віднімання, ділення, множення) з числами, представленими в модифікованому дробовому форматі. Програма буде реалізована з використанням PHP/MySQL, забезпечуючи таким чином кросплатформеність. Всі розрахунки виконують на серверній стороні, що дозволяє користувачеві не замислюватися про необхідність використання більш потужного комп'ютера.
Програма дозволить вводити формулу, в якій можуть бути використані як змінні, так і числа в експоненційній формі. Всі числа будуть переведені у відповідний модифікований формат, а потім за допомогою розроблених алгоритмів будуть проведені розрахунки. Результати будуть представлені як у вигляді дробу, так і у відповідному форматі. Більш того, програма буде динамічно змінювати розрядність. Таким чином, числа які вміщаються в формат меншої розрядності будуть збережені в ньому, якщо при перекладі у формат або після виконання операції число не вміщається в дану розрядну сітку, то буде зроблений перехід до більшої розрядності. Це буде однією з особливостей даного програмного продукту.
При написанні даного реферату, магістерська робота не закінчена. Остаточне завершення планується до грудня 2014 року. Роботу можна отримати у автора або керівника після її здачі.
Висновки
У рамках даної роботи описані існуючі формати представлення чисел, а також більш нові модифіковані формати для зберігання чисел з плаваючою комою. Також реалізовано програмний додаток, що дозволяє працювати з числами в модифікованому форматі. При написанні даного реферату, магістерська робота не закінчена. Остаточне завершення планується до грудня 2014 року. Роботу можна отримати у автора або керівника після її здачі.
Список джерел
1. Аноприенко А.Я., Иваница С.В., Кулибаба С.В. Особенности представления постбинарных вещественных чисел в контексте интервальных вычислений и развития аппаратного обеспечения средств компьютерного моделирования // Моделирование и компьютерная графика / Материалы IV международной научно—технической конференции – 5—8 октября 2011 г. Донецк, ДонНТУ. – 2011. С. 13—19.
2. Бесплатные программы SoftElectro. Программа IEEE754 — конвертор чисел формата IEEE 754 c абсолютной точностью представления результата. Електроний ресурс. Режим доступу: http://www.softelectro.ru/program.html.
3. Аноприенко А.Я., Иваница С.В. Постбинарный компьютинг и интервальные вычисления в контексте кодо—логической эволюции. — Донецк, ДонНТУ, УНИТЕХ, 2011. — 244 с.
4. Loh E., Walster G. Rump’s Example Revisited // Reliable Computing 8: 2002, p. 245–248.
5. Петров Ю.П. Обеспечение надежности и достоверности компьютерных расчетов. — СПб: БХВ—Петербург, 2008. — 160 с.
6. Аноприенко А.Я., Иваница С.В. Особенности постбинарного кодирования на примере интервального представления результатов вычислений по формуле Бэйли—Боруэйна—Плаффа // Научные труды Донецкого национального технического университета. Серия: «Информатика, кибернетика и вычислительная техника» (ИКВТ—2010). Выпуск 11 (164). – Донецк: ДонНТУ, 2010. С. 19—23.
7. Аноприенко А.Я., Иваница С.В. Интервальные вычисления и перспективы их развития в контексте кодо—логической эволюции // Научные труды Донецкого национального технического университета. Серия «Проблемы моделирования и автоматизации проектирования динамических систем» (МАП—2010). Выпуск 8 (168): Донецк: ДонНТУ, 2010. С. 150–160.
8. Moore R.E. Interval analysis. Eiiglewood Cliffs / R.E. Moore — N.J.:Prentic—e—llall, 1966.
9. Иваница С.В., Аноприенко А.Я. Особенности реализации операций тетралогики // Научные труды Донецкого национального технического университета. Серия: «Информатика, кибернетика и вычислительная техника» (ИКВТ—2011). Выпуск 13 (185). – Донецк: ДонНТУ, 2011. С. 134—140.
10. IEEE Standard for Floating—Point Arithmetic (IEEE 754). Електроний ресурс. Режим доступу: http://en.wikipedia.org/wiki/IEEE_754—2008
11. Douglas N. Arnold Some disasters attributable to bad numerical computing / Електроний ресурс. Режим доступу: http://www.ima.umn.edu/~arnold/disasters — Загл. с экрана.
12. Brisebarre N. Floating—Point Arithmetic / F. Dinechin, C. Jeannerod, V. Lefevre, G. Melquiond, J. Muller, N. Revol, D. Stehle, S. Torres — Laboratoire LIP, Projet Arenaire CNRS, INRIA, Ecole Normale Superieure de Lyon. — France, 2009 — 16 р.
