Реферат по теме выпускной работы
При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: январь 2015 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.
СОДЕРЖАНИЕ
- Введение
- 1. Цель работы и задачи исследования
- 2. Обоснование темы и краткий анализ состояния вопроса
- 3. Моделирование поведение пузырька и частицы при столкновении
- 3.1. Описание метода численного моделирования поведения фаз при образовании комплекса флотации
- 3.2. Проверка работоспособности численной модели и настройки ее параметров
- 4. Исследование влияния угла столкновения с частицей на траекторию движения воздушного пузырька
- Библиографический список
ВВЕДЕНИЕ
В мировой практике наблюдается общая тенденция ухудшения качества минерального сырья, добываемого что связано с выработкой запасов, богатых по содержанию ценных полезных компонентов и общим ухудшением горно - геологических условий эксплуатации месторождений[2-4]. Роль процессов обогащения поэтому с позиций обеспечения различных отраслей промышленности качественным сырьем для дальнейшей переработки постоянно увеличивается.
Практически все технологические процессы происходят в результате взаимодействия фаз, участвующих в них, друг с другом. Обогащение как способ разделения смеси минералов на основании различия в их физических свойствах не является исключением. При обогащении происходит механическая, физико - химическая, а также химическое взаимодействие фаз, участвующих: твердой, жидкой и газообразной. Одним из сложных процессов является флотация, показатели которой зависят в основном от поверхностных свойств взаимодействующих фаз. При флотации минеральные частицы взаимодействуют с реагентами и воздушными пузырьками в водной среде. Эти взаимодействия представляют значительную трудность для исследования, поскольку они динамичны, находятся под влиянием большого числа физических и химических факторов и происходят в маленьком масштабе.
Процесс флотации доведен до широкого практического использования в рудной практике в результате многолетних теоретических исследований и разработки технологии. Широкомасштабные исследования проводились многими отечественными и зарубежными учеными в 50-70-е годы двадцатого века. Флотация применяется и в угольной промышленности. Современные отечественные и зарубежные исследования направлены на поиск и разработку новых способов обогащения тонких классов угля и шламов, включая нетрадиционные способы относительно угольного сырья, а также на совершенствование уже известных. Следует отметить, что среди других полезных ископаемых угля занимает особое место как одна из основных составляющих в топливно - энергетическом комплексе Украины.
Проблемы, связанные с обработкой и обогащением мелких и тонких классов минерального сырья по-прежнему остаются актуальными, что вызвано снижением качества полезных ископаемых, добываемых. Для угля это выражается прежде всего в постоянном увеличении количества и зольности шламов в рядовом угле.
Флотация является единственным наиболее продуктивным процессом, который позволяет при обогащении угля коксующихся марок, доказывать зольность товарного концентрата до необходимой кондиции. Кроме того, флотация обеспечивает регенерацию оборотной воды от твердой фазы, имеет важное значение при использовании замкнутых водно - шламовых циклов. На рисунке 1 представлен пример работы флотационной машины.
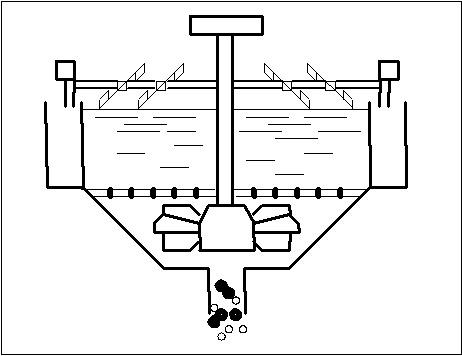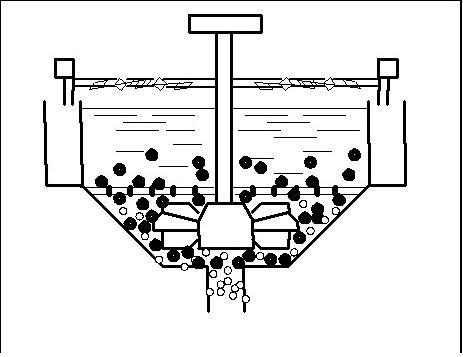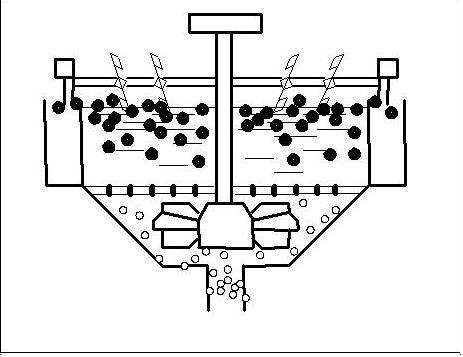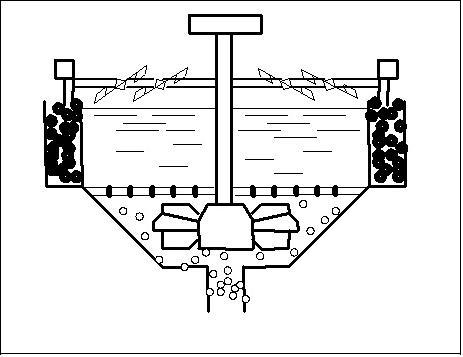
Рисунок 1 - Пример работы флотационной машины
(8
картинок, 22 кадра/с, объем - 396кб)
В производственных условиях при обогащении угля в последнее время стремятся уйти от метода флотации разделения и заменить его гравитационными процессами, например, винтовой или конусной сепарацией. Особенно широко этот процесс распространился на обогащение энергетического угля, где глубина обогащения выше 6мм. Такие меры вызваны дороговизной реагентов и их узкой номенклатурой, а также рядом трудностей технологического характера, связанных с необходимостью дальнейшей термической сушки пенного и обезвоживания камерного продукта до транспортабельного состояния. Но для концентратов, используемых для коксования, великая 0-0,2 мм. флотация прежнему не имеет альтернативы и представляет определенный интерес для исследователей.
Несмотря на исследования, проводившиеся до настоящего времени остаются вопросы, требующие уточнения и дополнения. Особенно большие трудности возникают при изучении процессов, происходящих на микроуровне. К таким процессам следует отнести в первую очередь взаимодействия фаз при их столкновении и образовании комплекса флотации в ходе элементарного акта флотации. Без понимания природы тонких явлений, происходящих практически невозможно развитие технологии флотационного обогащения и техники для его реализации. Изучение физических процессов, сопровождающих формирование комплекса «минерал – пузырь» будет способствовать повышению эффективности флотации. Таким образом тема магистерской работы является актуальной
1. ЦЕЛЬ РАБОТЫ И ЗАДАЧИ ИССЛЕДОВАНИЯ
Цель работы: изучение процессов образования флотационного комплекса при процессе флотации.
Задачи исследования:
- исследование флотации угольных частиц на микроуровне, проведение имитационного эксперимента поставлено с мытой определения параметров взаимодействия частиц и пузырьков при образовании флотационного комплекса;
- исследование влияния угла столкновения с частицей на траекторию движения воздушного пузырька.
2. ОБОСНОВАНИЕ ТЕМЫ И КРАТКИЙ АНАЛИЗ СОСТОЯНИЯ ВОПРОСА
Технология флотации широко применяется как метод обогащения не только в рудной, но и в углеобогатительной практике. Многолетние исследования и разработка технологии, проводились ведущими отраслевыми и научно - исследовательскими институтами при активном участии производственников, создали объективные предпосылки для доведения процесса флотации к широкому практическому применению в горно - обогатительной промышленности для обогащения тонких шламовых частиц позволяет получать концентраты требуемого качества.
Несмотря на исследования, проводившиеся до настоящего времени остаются вопросы, требующие уточнения и дополнения. Особенно большие трудности возникают при изучении процессов, происходящих на микроуровне. К таким процессам следует отнести в первую очередь взаимодействия фаз при их столкновении и образовании комплекса флотации в ходе элементарного акта флотации. Без понимания природы тонких явлений, происходящих практически невозможно развитие технологии флотационного обогащения и техники для его реализации. Изучение физических процессов, сопровождающих формирование комплекса «минерал - пузырь» будет способствовать повышению эффективности флотации. Так как взаимодействия фаз динамические во времени и находятся под влиянием большого числа физических и химических факторов и происходят в маленьком масштабе. Лабораторные испытания не всегда показывают удовлетворительную точность, является утомительным и требуют затрат времени. Кроме того, некоторые стадии взаимодействия достаточно сложно исследовать экспериментальным путем. Аналитические же исследования часто дают результаты, идеализированные.
3. МОДЕЛИРОВАНИЕ ПОВЕДЕНИЕ ПУЗЫРЬКА И ЧАСТИЦЫ ПРИ СТОЛКНОВЕНИИ
3.1. Описание метода численного моделирования поведения фаз при образовании комплекса флотации
Одним из современных вариантов решения этой проблемы является численное моделирование, которое сочетает в себе динамику, точность и рассмотрение широкого спектра деталей[1]. По сравнению с массивом горных пород частицы, разделяемых имеют действительно комплексную поведение: они перемещаются в процессе флотации и подвергаются множественным актам образования и разрушения комплексов флотационных. Эти процессы управляются физическими и химическими свойствами поверхности минералов и свойствами реагентов, добавляемых в процесс. На рисунке 2 представлена базовая схема взаимодействия элементов.
Метод дискретных элементов был сначала развит в геомеханике для моделирования поведения пород под действием горного давления [5, 6]. Этот метод был позднее успешно применен для описания взаимодействия частиц породы и течения потоков [8, 9, 10]. Данная модель базируется на том же приближении, что и модели, представленные в работах [7, 8, 9].

Рисунок 2 - Схема взаимодействия двух элементов элементов
Взаимодействующие элементы имеют шарообразную форму с радиусами R1 и R2. Любая частица движется под действием силы F1 или F2 и вращается в соответствии с законом Ньютона в прямоугольной системе координат X-Y, если она ускоряется моментами М1 и М2.
Движения частиц, разделяемых рассматриваются в дискретные периоды времени. В компьютерной реализации эти периоды моделируются как циклы. Координаты центров тяжести X1, Y1 и X2, Y2, скорости V1 и V2, и силы являются постоянными в пределах цикла и перечисляются на каждом цикле счета [11].
Программа выполняет моделирование перемещения в пространстве и взаимодействия отдельных и связанных в группы элементов. Работа программы базируется на основных законах механики: законе Гука и втором и третьем законах Ньютона.
Работа с программой состоит: 1) в подготовке файла исходных данных; 2) выполнении расчета; 3) изучении полученных результатов. Файл исходных данных содержит информацию о пространственном расположении элементов, их характеристики, связи между собой и действующие внешние силы. Расчет зависимости от количества соединительных элементов и возможностей компьютера может занимать время от нескольких минут до суток. Полученные результаты представляются в графическом виде, который отражает положение всех элементов в конкретные моменты времени.
Метод моделирования кинетики взаимодействия фаз в процессе флотации основан на моделировании динамики движения частиц и пузырьков в жидкой среде. Алгоритм расчета предполагает замену реальных твердых зерен и воздушных пузырьков частицами в форме шара, которые перемещаются независимо друг от друга и взаимодействуют посредством прямых столкновений. В процессе моделирования циклически осуществляется последовательный перебор всех элементов в порядке возрастания их порядкового номера. При этом перечисляются координаты X, Y, скорости V и действующие силы F. Наиболее важной частью алгоритма является определение дистанции между элементами D и вычисления их перекрытия Δl (нахлестки).
В результате рассчитывается прирост скорости на каждом цикле в соответствии с формулой:
dVy = G·dt, (1)
где ΔVy – вертикальное приращение скорости, м/с;
G – ускорение свободного падения, м/с²;
dt – приращение времени за один цикл, с.
Затем производится перемещение элементов на новую позицию соответственно сформированным скоростям V и приращению времени dt по формулам:
X = X + dVxdt, (2)
Y = Y + dVydt, (3)
где X – новое горизонтальное положение элемента (координата), м;
dVx – горизонтальный прирост скорости, м / с;
Y – новое вертикальное положение элемента (координата), г.
После перемещения всех элементов на новые позиции выполняется проверка взаимодействия и на основании полученных зашморгувань Δl (перекрытий) элементов вычисляются приращения действующих сил по формуле:
dF = k·Δl, (4)
где dF – прирост силы, H;
k – коэффициент жесткости, Н / м;
Δl – нахлестки элементов, г.
Следует отметить, что отдельно вычисляются и фиксируются силы, действующие в горизонтальных и вертикальных направлениях, а также момент сил, вызывает повороты элементов относительно своих центров.
Чтобы учесть реальные процессы, протекающие при взаимодействии частиц и пузырьков в процессе флотации, а именно, инерционность, сопротивление среды и потери энергии при переходе из одного состояния в другое, в алгоритм введены коэффициенты, учитывающие потери энергии в этих случаях. В частности, есть возможность задавать сопротивление среды элементам движущихся по формуле Стокса, а также коэффициент потерь энергии при взаимодействии элементов.
Для учета силы трения, возникающей при взаимодействии отдельных элементов, в процессе вычисления приращений сил учитываются указанные в исходных данных коэффициенты трения.
С учетом сказанного выше формулу (1) и (4) примут вид:
dVy = qdt - 6·kv·R·Vy, (5)
dF = k·Δl – k·F·V – k·T·F, (6)
где kV – сопротивление среды (коэффициент демпфирования);
R – радиус элемента;
Vy – вертикальная составляющая скорости;
kF – коэффициент внутреннего сопротивления, определяемый взаимодействием элементов (коэффициент необратимости, потери энергии на протяжении взаимодействия);
kT – коэффициент трения;
F – равнодействующая сил, приложенных к элементуc.
После определения сил, приложенных ко всем элементов, выполняется перемещение элементов на новую позицию в соответствии со значениями этих сил. Затем происходит циклическое повторение вышеперечисленных операций.
На протяжении каждого цикла смежные частицы проверяются условия когезии и адгезии. Если частицы имеют приближения друг к другу на критическое расстояние, они слипаются между собой (две или несколько). Одновременно проверяются силы адгезии (когезии). Если они достигают определенных границ, слипшиеся комплексы разрушаются. Введена три черты для сил. А именно, частицы, слившихся должны отделиться, если они были сжаты в нормальном направлении на величину большую, чем предел сжатия Lt, или были срезаны в тангенциальном направлении относительно друг друга больше, чем предел сдвиги Ls, или изогнутые относительно соединения более, чем предел искажения Lb.
Исходные данные для выполнения расчета готовятся в текстовом файле с помощью встроенного или любого другого редактора, работающего с неформатированный текст. Программа позволяет готовить и редактировать файл исходных данных полностью автоматически. Это ускоряет процесс подготовки и снижает вероятность возникновения ошибок при задании начальных параметров.
Таким образом истинная динамическое поведение взаимодействующих фаз моделируется при их обогащении флотации. Компьютерные коды развиты в среде Дельфи-3. Моделирование поведения двумерного комплекса на протяжении сотен тысяч циклов, содержащих сотни части, может быть закончено за разумный период времени благодаря средствам объектного программирования.
3.2. Проверка работоспособности численной модели и настройки ее параметров
Перед использованием описанной выше численной модели для исследования процесса взаимодействия угольных частиц и пузырьков необходимо выполнить проверку правильности подобранных факторов с учетом свойств фаз, участвующих чтобы модель адекватно отражала реально протекающие процессы. Для первоначальной настройки модели выполнено моделирование отрыва воздушного пузырька от минеральной пластинки. Этот эксперимент компьютерного моделирования был проведен в условиях, воспроизводящих физический эксперимент [2].
Уравнение перемещения воздушного пузырька вдоль наклонно расположенной пластинки в упрощенном виде:
mdv/dt = Fв·Sin α – Fc – f·(Fв - m·g)·Cos α, (7)
где m – масса пузырьки;
Fв – выталкивающая сила;
Fc – сила сопротивления перемещению пузырьки, связанная с сопротивлением жидкости и с силой, определяемой взаимодействием приповерхностных слоев гидратов пузырьки и пластинки;
f – коэффициент трения.

Рисунок 3 - Схема сил, действующих на пузырек при его перемещении вдоль наклонной пластинки
Массой пузырьки и силой его тяжести можно пренебречь ввиду их малое значение по сравнению с другими действующими силами.
Для выполнения исследований стеклянная пластинка готовилась следующим образом. На поверхность пластинки наклеивался тонкий слой угольного порошка. Затем воздушный пузырек контактировала с этой пластинкой, погруженной в воду, и прикреплялась к стороне с наклеенными угольными частицами. После этого пластинка постепенно наклонялась до тех пор, пока пузырек воздуха не отрывалась от пластинки и не всплывала. Угол наклона пластинки, при котором происходит отрыв пузырька от ее поверхности, считается критическим. По величине критического угла наклона пластинки судят об активности флотации минерала изучаемого слой которого наклеен на поверхности пластинки.
В компьютерной модели поверхность пластинки с наклеенным на нее угольным порошком моделировалась набором мелких угольных частиц, которые были прочно прикреплены друг к другу с помощью подбора коэффициентов нормальной деформации. Результаты моделирования представлены в графической форме на рисунке 4.

Рисунок 4 - Компьютерные фрагменты исследования движения воздушного пузырька от дна кюветы вдоль пластинки в течении 1300000 циклов
На рис. 4 показаны концевые фрагменты компьютерных фильмов после окончания 1.3 с (1300000 циклов). Один цикл моделирования отвечал 10-6 с реального времени эксперимента. Модель дает возможность проследить практически на каждом цикле счета изменение положения координат центра тяжести всех элементов, радиуса пузырька, его скорость. Пузырек имела диаметр 2 мм и устойчиво закреплялся на пластинке при ее наклоне до 50 (рис. 4, а).
В процессе моделирования было замечено, что пузырек при перемещении вдоль пластинки вращается вокруг своей оси. Это было определено по изменению положения радиуса пузырька. При этом пузырек несколько деформировалась и вытянулась вдоль пластинки, формируя 5 элементарных контактов с ее поверхностью. Точки контакта увеличивают прочность соединения пузырьки с поверхностью пластинки и пузырь остается прикрепленным к пластинке.
При наклоне пластинки до угла в 15° происходит продвижение пузырька воздуха вперед и вверх, к другому концу пластинки (рис. 4, б). Однако скорость перемещения пузырька оставалась незначительной - по 1.3 с пузырек переместилась на расстояние около 29мм, т.е. пузырек двигаласья со средней скоростью 22 мм / с.
При угле наклона пластинки равному 25° пузырек за это же время преодолевала расстояние около 90мм, перемещаясь вдоль пластинки (см. рис. 4, в). Таким образом, средняя скорость перемещения пузырька при заданных начальных условиях составила около 69 мм / с.
При задании угла наклона пластинки равным 55° наблюдалось быстрое перемещение пузырька вдоль поверхности всей пластинки, его отрыв и дальнейшее резкое всплытие (рис. 4, г).
Полученные значения свидетельствуют о том, что для гидрофильной поверхности скорость перемещения пузыри увеличивается. Быстрое продвижение пузырька вдоль пластинки при увеличении угла ее наклона вызвано увеличением результирующей силы, которая значительно превышает силы сопротивления движению всплывающей пузырьки.
В работе [3] приведены данные аналогичного эксперимента, выполненного для всплытия пузырьков вдоль наклонной пластинки из органического стекла и стальной.
По данным практики оптимальная скорость перемещения газообразной фазы для пузырьков крупности флотации составляет 50-150 мм / с при углах наклона пластинок в пределах 25-55 градусов.
Таким образом, проведено моделирование продемонстрировало приемлемое поведение компьютерной модели при моделировании отдельных стадий процесса взаимодействия фаз при обогащении флотации и доказало ее эффективность.
4. ИССЛЕДОВАНИЕ ВЛИЯНИЯ УГЛА СТОЛКНОВЕНИЯ С ЧАСТИЦЕЙ НА ТРАЕКТОРИЮ ДВИЖЕНИЯ ВОЗДУШНОГО ПУЗЫРЬКА
Для возможности качественного сравнения результатов имитационного моделирования и натурного эксперимента было выполнено компьютерное моделирование закрепления частицы на пузырьке для следующих условий. Угольная частица диаметром 0,29 мм падала со скоростью 0,3 мм/с на воздушную пузырь диаметром 2 мм, истекающего со скоростью 12 мм/с. Точка встречи смещалась относительно центра пузыри на 100, 200, 300, 400, 500, 600, 700, 800, 900 и 1000 микрон. Это смещение может быть рассмотрено как эксцентриситет относительно центра и направления силы тяжести. Начальная модель представлена на рисунке 5.

Рисунок 5 - Начальная модель
Здесь показаны: x0 - X0 = e - эксцентриситет при встрече частицы и пузырьки, φ0 и φi - начальный угол касания частицы и текущий, соответственно; R и r - положение радиуса пузырька и частицы, соответственно; L - дуговой путь центра тяжести частицы; а также координаты центров тяжести пузырьки и частицы.
Процесс взаимодействия частицы, падает, и всплывающей вверх пузырьки моделировался течение 80000 циклов. Один цикл счета отвечал 10-6с натурального времени.
Координаты центров тяжести элементов и состояние комплекса накапливались в файле каждые 200 циклов. Для расчетов принята взаимодействие воздушного пузырька диаметром 2,5 мм (2000 пикселей) и угольной частицы размером 0,36 мм (290 мкм) сферической формы.
Исследования, проведенные ранее с применением компьютерного моделирования, позволили установить, что при столкновении воздушного пузырька и минеральной частицы тангенциальная компонента скорости частицы возрастает с увеличением эксцентриситета между центром пузырьки и точкой встречи с частицей. Именно эта компонента скорости при увеличении до критического значения вызывает проскальзывание частицы относительно поверхности пузырька и в итоге ее отрыв.
Кроме того, определенный интерес представляют другие параметры перемещения частицы относительно пузырьки и комплекса в целом.
На рисунке 6 представлены расчетные графики траекторий перемещения центра тяжести частицы без учета всплытия пузырька.

Рисунок 6 - Траектория центра тяжести частицы без учета всплывания пузырька при различных эксцентриситетах столкновения
Вертикальные линии на рисунке 6 соответствуют траектории движения частицы до столкновения с пузырем. При образовании агрегата флотации частица закрепляется на пузырьке и движется по его поверхности или вместе с ним. Затем происходит отрыв частицы при эксцентриситете встречи 100 и 1000 пикселей, то есть 125 и 1250 мкм или при угле столкновения от 5 до 65°.
Таким образом, проведенные исследования кинетики взаимодействия фаз при флотационном обогащении путем компьютерного моделирования и сравнение результатов расчета и экспериментов показали приемлемую сходимость.
Как следует из данных, максимальное время существования комплекса флотации и совместного движения частицы и пузырьки наблюдается при минимальном значении угла столкновения.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- Гарковенко Е.Е. Взаємодія фаз при обезводненні тонких класів вугілля // Збагачення корисних копалин. Дніпропетровськ. - 2001. - №13(54). - с. 116-121.
- Ємельянов Д.С. Основи флотації вугілля. - Харків: ХГУ, 1958. - 290 c.
- Гарковенко Е.Е., Назимко Е.И., Самойлов А.И., Папушин Ю.Л. Особливості флотації і обезводнення тонкодисперсних вуглевмісних матеріалів. Донецьк: Норд-прес. - 2002. - 266 с.
- Гарковенко Е.Е., Назимко Е.И., Самойлов А.И и др. Особенности флотации и обезвоживания тонкодисперсных углесодержащих материалов. – Донецк: Норд-пресс. – 2002. – 256 с.
- S. S. Kim, B. I. Morsi, and S.–H. Chiang, Statistical Analysis of the Performance of a Selective Agglomeration Process Using n-heptane as Agglomerant, Coal Preparation, 15, 51-70 (1994).
- P. A. Cundall, O. D. L. Strack, A discrete numerical model for grannular assemblies, Geotechnique, 29:1, 47–65 (1979).
- Звягильский Е.Л. Изучение кинетики обрушения толщи над горизонтальными выработками мелкого заложения // Проблемы горного давления. – 1999. - № 2. – С. 17-29.
- Bruno M. S. et al. 1996. Some influences of saturation and fluid flow on sand production: Laboratory and Discrete Element Model Investigations. SPE 36534, Proc. 1996 SPE Ann. Tech. Conf., Denver, Colorado, 6–9 October, 447–461.
- O'Connor P.M., John R. Torczynski Dale S. Preece; Justin T. Klosek; John R. Williams Discrete Element Modeling of Sand Production Int. J. Rock Mech. & Min. Sci. 34:3–4, Paper No. 231.
- P. F. Whelan and D. J. Brown, Particle-Bubble Attachment in Froth Flotation, Bull. Inst. Min. a. Met., No 591, 593 (1956).
- Митрофанов С.И. Селективная флотация. М.: Металлургиздат. - 1958. – 726 с.
