Abstract
This master's work is not completed yet. Final completion: January 2015. Full text of the work and materials on the topic can be obtained from the author or his adviser after that date.
ABSTRACT
- Introduction
- 1. Basics of numerical model
- 2. Validation of the model
- 2.1. Air bubble take-off from a mineralized plate
- 3. Trajectory of a mineral particle during its impact with an air bubble
- References
INTRODUCTION
Problems associated with the processing and enrichment of small and thin classes of minerals remain relevant, which is caused by a decrease in the quality of minerals mined. Coal is expressed primarily in the constant increase in the amount of ash and sludge in mine coal.
Flotation is the single most productive process that allows the enrichment of coking coal, bring ash salable concentrate to the desired condition. In addition, flotation provides regeneration of recycled water from the solid phase is important when using a closed water - sludge cycles. Figure 1 - an example of a flotation machine.

Figure
1 - Example of flotation machine
(8
image's,22 frames/sec, volume - 396kb)
The interaction of phases is the basis of majority of technologies for mineral processing. Typical examples are interaction of air bubbles with reagents and minerals during their flotation, mineral-water interfaces in dewatering of fine coal, etc. These interactions are very hard to investigate because they are dynamical, impacted by long array of physical and chemical factors and occur in a small scale. The mentioned above processes have been traditionally studied by laboratory experiments. These tests are tedious and time consuming, although indicate unsatisfactory accuracy. Analytical investigations yield idealized results. One of the powerful alternatives to deal with the problem is a numerical simulation which combines dynamics, accuracy and consideration of sophisticated details. This model is based on discrete elements. In this paper a computer model for simulation of kinetics of phase’s interaction during mineral processing will be considered.
1. BASICS OF NUMERICAL MODEL
Discrete elements method has been originally developed in geomechanic to simulate rock mass behavior under action of ground pressure, according to Cundall1. This method has been later applied to describe interaction of rock particles and fluid flow, according papers [2, 3]. The authors of this paper developed a model for particle interaction during mineral processing. The model is based on the same approach as the models cited in papers [1-3]. In addition, essential peculiarities of the mineral processing have been introduced to simulate dynamics of particles interaction. They move and undergo to multiple acts of adhering and disintegrating. These processes are governed by physical and chemical properties of the surfaces of minerals and reagents.
A pair of interacting particles, namely mineral particle and air bubble indicated in Figure 2.
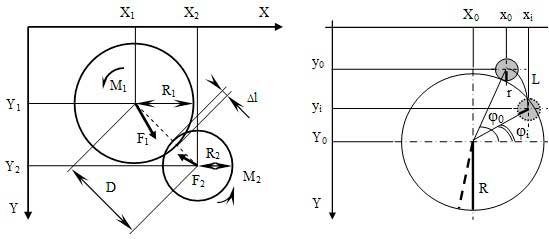
Figure 2 – Particle and bubble interaction on approaching (left) and during flotation (right)
The particles are circular with radiuses R1 and R2(see Figure 1, left). Any particle moves under action of a force F1 or F2 and rotate according the Newton law in Cartesian system of coordinates X-Y if is accelerated by moments М1 and М2.
Movements of separate particles are considered in discrete periods of time. In computer realization, these periods are simulated as cycles. Coordinates of the centers of gravity X1, Y1 and X2, Y2, velocities V1 and V2, and the forces are constantly recalculated on every cycle.
All particles move under action of resultant acceleration G which is caused by gravity, Archimedes (displacement) force, damping force of the media resistance and impacts of adjacent neighbors. As a result, velocity increment is calculated at every cycle according a formula:
ΔV = G·Δt - kv·Vy, (1)
where ΔV – is the increment of the velocity, m/s;
G – is an acceleration, m/s²;
Δt – is the time of increment at a cycle, s;
kv - is the media resistance (damping factor).
Then the particles move to the next position according components of the velocity and time increment:
X = X + ΔVx·Δt, (2)
Y = Y + ΔVy·Δt, (3)
where X and Y are new horizontal and vertical coordinates of a particle, m;
ΔVx and ΔVy - are horizontal and vertical velocity increments, m/s.
After cyclical movement of a particle to a new position, a distance D between adjacent particles has to be checked and an overlap Δl is calculated. Then force increment is calculated as:
ΔF = k·Δl - kF·V - kT·F, (4)
where ΔF – is the force increment, N;
k – is a stiffness factor, N/m;
kT and kF - are the friction factor and coefficient of irreversibility (loss of energy during interaction);
F - is a resultant force, N.
During every cycle, adjacent particles are checked for adhesion or cohesion conditions. If the particles have approached to each other at a critical distance, they stick between or among themselves. The forces of the adhesion are examined instantaneously. If they exceed certain limits, stuck particles disintegrate. Three limits of the adhesion have been introduced. Namely the collided particles may disjoin if they were tensed in normal direction more than limit of tension Lt, or have been shifted in tangential direction relatively each other more than shear limit Ls, or were bent relatively the joint more than buckling limit Lb. In such a way, truly dynamic behavior of minerals has been simulated during their processing.
2. VALIDATION OF THE MODEL
We have made a set of computer simulations to accumulate sufficiently versatile data. The next computer experiments have been accomplished: air bubble take-off from a mineralized plate has been investigated for different inclination of the plate relatively horizon; time of coal particle residence on an air bubble was investigated for different boundary and initial conditions; trajectory, velocity and acceleration of a mineral particle have been registered during its impact with an air bubble at different eccentricity.
2.1 Air bubble take-off from a mineralized plate
The first test of the computer model has been conducted in a special simulation that reproduced a physical experiment. The air bubble has been attached on the bottom side of a horizontal plate submerged into water. Dust of mineral was preliminary pasted to the plate surface. Then the plate had tilted gradually until the bubble detached at a critical angle and floated. Figure 3 - Computer fragments motion study of the air bubble from the bottom.
In computer model, the plate has been simulated with a set of small particles which were firmly attached one to another. One cycle of simulation corresponded to 10-6s. The bubble had diameter 2.5 mm and was stable during inclination of the plate at 50. It stretched along the plate and formed 5 elementary contacts with the plate surface, according research4. These contacts reinforced the joint and the bubble became stable. Inclination of the plate at 150 promoted the bubble to move forward however speed of the movement was negligible. Experimental value of the critical angle was 130 for a pure coal surface, according to Emelyanov[5]. After increasing the tilt up to 250, the bubble ran the distance approximately 6 mm for 1.3 s. Tilt of 550 caused the bubble to run along the whole plate and to take off.
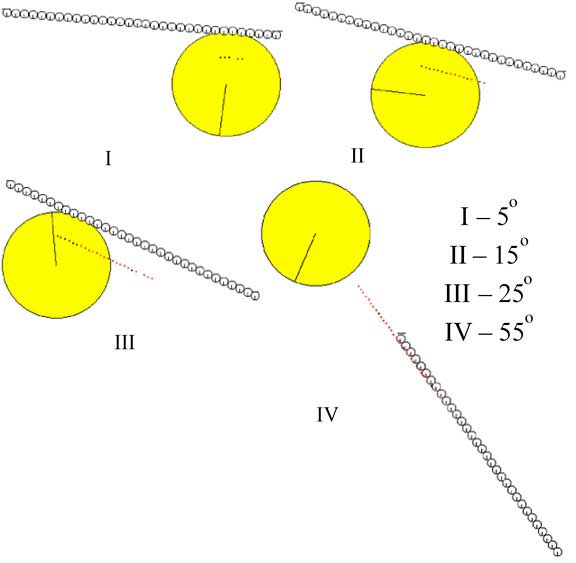
Figure 3 - Computer fragments motion study of the air bubble from the bottom of the cell along the plate during cycles 1300000
3. TRAJECTORY OF A MINERAL PARTICLE DURING ITS IMPACT WITH AN AIR BUBBLE
Elementary act of particle-bubble attachment in froth flotation was investigated by Whelan P.F. and Brown D.J.[6]
The authors concluded that after impact, normal velocity of the particle reduced dramatically. The more particle was shifted relatively the center of the bubble, the more tangential velocity of the particle and the less probability of its attachment.
Computer simulation of particle attachment (Figure 4) has been made for the next conditions.
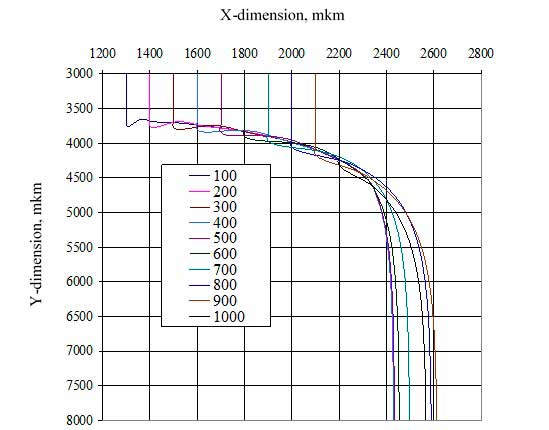
Figure 4 – Computer modeling data
Coal particle 0.29 mm in diameter were dropped to a floating air bubble 2 mm in diameter. Point of meeting was shifted relatively center of the bubble from 100 to 1000 micron (positions from 1 to 10).
As reported in Figure 4, calculated trajectories are similar to those experimental. Investigation of the computer movie corroborated the fact of sharp reduction of particle normal velocity after impact. Tangential component of particle velocity grows as eccentricity increases.
As follows from the data, the maximum lifetime of the complex flotation and joint motion particles and bubbles observed at the minimum angle of impact.
REFERENCES
- Cundall, P.A., Strack, O.D.L. A discrete numerical model for grannular assemblies. Geotechnique, vol. 29, no.1. 1979. pp. 47–65;
- Bathurst, R.J., Rothenburg, L. Observations on stress-force-fabric relationships in idealized grannular media. Mech. of Mat., vol. 9. 1990. pp. 65–80;
- Bruno, M. S. et al. Some influences of saturation and fluid flow on sand production: Laboratory and Discrete Element Model Investigations. SPE 36534. Proceedings 1996 SPE Ann. Tech. Conf., Denver, Colorado, 6–9 October, 1996. pp. 447–461;
- Garkovenko E.E. et al. Features of fine coal materials flotation and dewatering. Donetsk. 2002, 266 p. Russian text;
- Emelyanov D. S. Coal flotation basics. Kharkov University. Kharkov, 1958, 216 p. Russian text;
- Whelan, P. F., Brown, D. J. Particle-Bubble Attachment in Froth Flotation. Bull. Inst. Min. a. Met., No 591, 593 (1956).
