Реферат за темою випускної роботи
При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: січень 2015 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.
ЗМІСТ
- Вступ
- 1. Мета роботи і завдання дослідження
- 2. Обгрунтування теми і короткий аналіз стану питання
- 3. Моделювання поведінки бульбашки і частинки при зіткненні
- 3.1. Опис методу чисельного моделювання поведінки фаз при утворенні комплексу флотації
- 3.2. Перевірка працездатності чисельної моделі і налаштування її параметрів
- 4. Дослідження впливу кута зіткнення з частинкою на траєкторію руху повітряної бульбашки
- Бібліографічний список
ВСТУП
У світовій практиці спостерігається загальна тенденція погіршення якості мінеральної сировини, що добувається, що пов'язано з виробленням запасів, багатих за змістом цінних корисних компонентів і загальним погіршенням гірничо-геологічних умов експлуатації родовищ[2-4]. Роль процесів збагачення тому з позицій забезпечення різних галузей промисловості якісною сировиною для подальшої переробки постійно збільшується.
Практично усі технологічні процеси відбуваються в результаті взаємодії фаз, що беруть участь в них, один з одним. Збагачення як спосіб розділення суміші мінералів на підставі відмінності в їх фізичних властивостях не є виключенням. При збагаченні відбувається механічна, фізико-хімічна, а також хімічна взаємодія фаз, що беруть участь: твердою, рідкою і газоподібною. Одним із складних процесів є флотація, показники якої залежать в основному від поверхневих властивостей взаємодіючих фаз. При флотації мінеральні частинки взаємодіють з реагентами і повітряними бульбашками у водному середовищі. Ці взаємодії представляють значну трудність для дослідження, оскільки вони динамічні, перебувають під впливом великого числа фізичних і хімічних чинників і відбуваються в маленькому масштабі.
Процес флотації доведений до широкого практичного використання в рудній практиці в результаті багаторічних теоретичних досліджень і розробки технології. Широкомасштабні дослідження проводилися багатьма вітчизняними і зарубіжними вченими в 50-70-і роки двадцятого століття. Флотація застосовується і у вугільній промисловості. Сучасні вітчизняні і зарубіжні дослідження спрямовані на пошук і розробку нових способів збагачення тонких класів вугілля і шламів, включаючи нетрадиційні способи стосовно вугільної сировини, а також на вдосконалення вже відомих. Слід зазначити, що серед інших корисних копалини вугілля займає особливе місце як одна з основних складових в паливно-енергетичному комплексі України.
Проблеми, пов'язані з обробкою і збагаченням дрібних і тонких класів мінеральної сировини як і раніше залишаються актуальними, що викликано зниженням якості корисних копалини, що добуваються. Для вугілля це виражається передусім в постійному збільшенні кількості і зольності шламів в рядовому вугіллі.
Флотація є єдиним найбільш продуктивним процесом, який дозволяє при збагаченні вугілля марок, що коксуються, доводити зольність товарного концентрату до необхідної кондиції. Крім того, флотація забезпечує регенерацію оборотної води від твердої фази, що має важливе значення при використанні замкнутих водно-шламових циклів. На рисунку 1 представлен приклад роботи флотаційної машини.
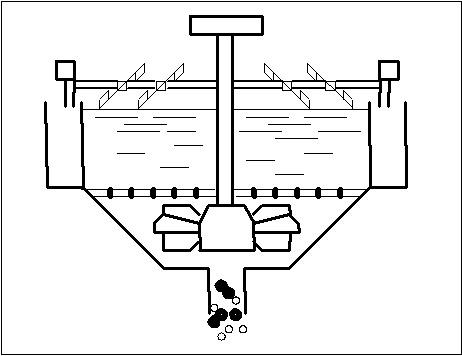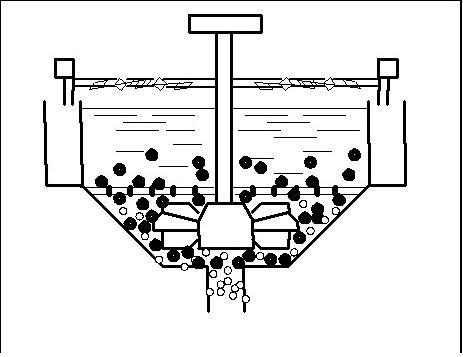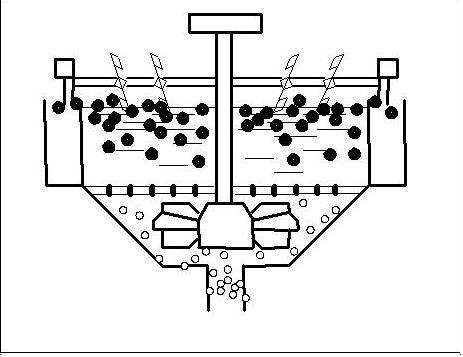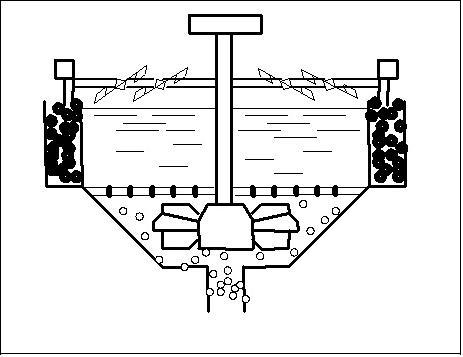
Рисунок
1 - Приклад роботи флотаційної машини
(8
картинок, 22 кадра/с, об'єм - 396кб)
У виробничих умовах при збагаченні вугілля останнім часом прагнуть піти від методу флотації розділення і замінити його гравітаційними процесами, наприклад гвинтовою або конусною сепарацією. Особливо широко цей процес поширився на збагачення енергетичного вугілля, де глибина збагачення вище 6мм. Такі заходи викликані дорожнечею реагентів і їх вузькою номенклатурою, а також рядом труднощів технологічного характеру, пов'язаних з необхідністю подальшої термічної сушки пінного і обезводнення камерного продукту до транспортабельного стану. Але для концентратів, використовуваних для коксування, великістю 0-0.2 мм. флотація як і раніше не має альтернативи і представляє певний інтерес для дослідників.
Незважаючи на дослідження, що проводилися, до теперішнього часу залишаються питання, що вимагають уточнення і доповнення. Особливо великі труднощі виникають при вивченні процесів, що відбуваються на мікрорівні. До таких процесів слід віднести в першу чергу взаємодії фаз при їх зіткненні і утворенні комплексу флотації в ході елементарного акту флотації. Без розуміння природи тонких явищ, що відбуваються, практично неможливий розвиток технології збагачення флотації і техніки для його реалізації. Вивчення фізичних процесів, які супроводжують формування комплексу «мінерал-бульбашка» сприятиме підвищенню ефективності флотації. Таким чином тема магістерської роботи є актуальною.
1. МЕТА РОБОТИ І ЗАВДАННЯ ДОСЛІДЖЕННЯ
Мета роботи: вивчення процесів утворення флотаційного комплексу при процесі флотації.
Завдання дослідження:
- дослідження флотації вугільних частинок на мікрорівні, проведення імітаційного експерименту поставлено з митою визначення параметрів взаємодії частинок і повітряних бульбашок при утворенні флотаційного комплексу;
- дослідження впливу кута зіткнення з частинкою на траєкторію руху повітряної бульбашки.
2. ОБГРУНТУВАННЯ ТЕМИ І КОРОТКИЙ АНАЛІЗ СТАНУ ПИТАННЯ
Технологія флотації широко застосовується як метод збагачення не лише в рудній, але і у вуглезбагачувальній практиці. Багаторічні дослідження і розробка технології, що проводилися провідними галузевими і науково-дослідними інститутами при активній участі виробничників, створили об'єктивні передумови для доведення процесу флотації до широкого практичного застосування в гірничо-збагачувальній промисловості для збагачення тонких шламових часток, що дозволяє отримувати концентрати необхідної якості.
Незважаючи на дослідження, що проводилися, до теперішнього часу залишаються питання, що вимагають уточнення і доповнення. Особливо великі труднощі виникають при вивченні процесів, що відбуваються на мікрорівні. До таких процесів слід віднести в першу чергу взаємодії фаз при їх зіткненні і утворенні комплексу флотації в ході елементарного акту флотації. Без розуміння природи тонких явищ, що відбуваються, практично неможливий розвиток технології збагачення флотації і техніки для його реалізації. Вивчення фізичних процесів, які супроводжують формування комплексу «мінерал-бульбашка» сприятиме підвищенню ефективності флотації. Так як взаємодії фаз динамічні в часі та перебувають під впливом великого числа фізичних і хімічних чинників і відбуваються в маленькому масштабі. Лабораторні випробування не завжди показують задовільну точність, є стомливими і вимагають витрат часу. Крім того, деякі стадії взаємодії досить складно досліджувати експериментальним шляхом. Аналітичні ж дослідження часто дають результати, що ідеалізуються.
3. МОДЕЛЮВАННЯ ПОВЕДІНКИ БУЛЬБАШКИ І ЧАСТИНКИ ПРИ ЗІТКНЕННІ
3.1. Опис методу чисельного моделювання поведінки фаз при утворенні комплексу флотації
Одним з сучасних варіантів вирішення цієї проблеми є чисельне моделювання, яке поєднує в собі динаміку, точність і розгляд широкого спектру деталей[1]. В порівнянні з масивом гірських порід частинки, що розділяються, мають дійсно комплексну поведінку: вони переміщаються в процесі флотації і піддаються множинним актам освіти і руйнування комплексів флотацій. Ці процеси управляються фізичними і хімічними властивостями поверхні мінералів і властивостями реагентів, що додаються в процес. На рис. 2 представлена базова схема взаємодії елементів.
Метод дискретних елементів був спочатку розвинений в геомеханіці для моделювання поведінки порід під дією гірського тиску[5, 6]. Цей метод був пізніше успішно застосований для опису взаємодії частинок породи і течії потоків[8, 9, 10]. Дана модель базується на тому ж наближенні, що і моделі, представлені в роботах[7, 8, 9].

Рисунок 2 - Схема взаємодії двох елементів елементів
Взаємодіючі елементи мають кулясту форму з радіусами R1 і R2. Будь-яка частинка рухається під дією сили F1 або F2 і обертається відповідно до закону Ньютона в прямокутній системі координат X-Y, якщо вона прискорюється моментами М1 і М2.
Рухи частинок, що розділяються, розглядаються в дискретні періоди часу. У комп'ютерній реалізації ці періоди моделюються як цикли. Координати центрів тяжіння X1, Y1 і X2, Y2, швидкості V1 і V2, і сили є постійними в межах циклу і перераховуються на кожному циклі рахунку [11].
Програма виконує моделювання переміщення в просторі і взаємодії окремих і пов'язаних в групи елементів. Робота програми базується на засадничих законах механіки : законі Гуку і другому і третьому законах Ньютона.
Робота з програмою полягає: 1) в підготовці файлу початкових даних; 2) виконанні розрахунку; 3) вивченні отриманих результатів. Файл початкових даних містить інформацію про просторове розташування елементів, їх характеристики, зв'язки між собою і діючі зовнішні сили. Виконання розрахунку залежно від кількості початкових елементів і можливостей комп'ютера може займати час від декількох хвилин до діб.
Метод моделювання кінетики взаємодії фаз в процесі флотації заснований на моделюванні динаміки руху часток і повітряних бульбашок в рідкому середовищі. Алгоритм розрахунку припускає заміну реальних твердих зерен і повітряних бульбашок частинками у формі кулі, які переміщаються незалежно один від одного і взаємодіють за допомогою прямих зіткнень. В процесі моделювання циклічно здійснюється послідовний перебір усіх елементів в порядку зростання їх порядкового номера. При цьому перераховуються координати X, Y, швидкості V і діючі сили F. Найбільш важливою частиною алгоритму є визначення дистанції між елементами D і обчислення їх перекриття Δl (зашморгування).
В результаті розраховується приріст швидкості на кожному циклі відповідно до формули:
dVy = G·dt, (1)
де ΔVy – вертикальне прирощення швидкості, м/с;
G – прискорення вільного падіння, м/с²;
dt – приріст часу за один цикл, с.
Потім проводиться переміщення елементів на нову позицію відповідно сформованим швидкостям V і збільшенню часу dt за формулами:
X = X + dVxdt, (2)
Y = Y + dVydt, (3)
де X – нове горизонтальне положення елементу (координата), м;
dVx – горизонтальний приріст швидкості, м/с;
Y – нове вертикальне положення елементу (координата), м.
Після переміщення усіх елементів на нові позиції виконується перевірка їх взаємодії і на підставі отриманих зашморгувань Δl (перекриттів) елементів обчислюються прирости діючих сил по формулі:
dF = k·Δl, (4)
де dF – приріст сили, H;
k – коефіцієнт жорсткості, Н / м;
Δl – зашморгування елементів, г.
Слід зазначити, що окремо обчислюються і фіксуються сили, діючі в горизонтальних і вертикальних напрямах, а також момент сил, що викликає повороти елементів відносно своїх центрів.
Щоб врахувати реальні процеси, що протікають при взаємодії часток і повітряних бульбашок в процесі флотації, а саме, інерційність, опір середовища і втрати енергії при переході з одного стану в інший, в алгоритм введені коефіцієнти, що враховують втрату енергії в цих випадках. Зокрема, є можливість задавати опір середовища елементам, що рухаються, згідно з формулою Стоксу, а також коефіцієнт втрат енергії при взаємодії елементів.
Для обліку сили тертя, що виникає при взаємодії окремих елементів, в процесі обчислення приростів сил враховуються вказані в початкових даних коефіцієнти тертя.
З урахуванням сказаного вище за формулу (1) і (4) наберуть вигляду:
dVy = qdt - 6·kv·R·Vy, (5)
dF = k·Δl – k·F·V – k·T·F, (6)
де kV – опір середовища (коефіцієнт демпфування);
R – радіус елементу;
Vy – вертикальна складова швидкості;
kF – коефіцієнт внутрішнього опору, визначуваний взаємодією елементів (коефіцієнт безповоротності, втрати енергії впродовж взаємодії);
kT – коефіцієнт тертя;
F – рівнодійна сил, прикладених до елементу.
Після визначення сил, прикладених до усіх елементів, виконується переміщення елементів на нову позицію відповідно до значень цих сил. Потім відбувається циклічне повторення перелічених вище операцій.
Впродовж кожного циклу суміжні частинки перевіряються на умови когезії і адгезії. Якщо частинки мають наближення одна до іншої на критичну відстань, вони злипаються між собою (дві або декілька). Одночасно перевіряються сили адгезії (когезії). Якщо вони досягають певних меж, злиплі комплекси руйнуються. Введена три межі для сил. А саме, частинки, що злилися, повинні відокремитися, якщо вони були стислі в нормальному напрямі на величину більшу, ніж межа стискування Lt, або були зрізані в тангенціальному напрямі один відносно одного більше, ніж межа зрушення Ls, або зігнуті відносно з'єднання більше, ніж межа викривлення Lb.
Початкові дані для виконання розрахунку готуються в текстовому файлі за допомогою вбудованого або будь-якого іншого редактора, працюючого з неформатованим текстом. Програма дозволяє готувати і редагувати файл початкових даних повністю автоматично. Це прискорює процес підготовки і знижує вірогідність виникнення помилок при завданні початкових параметрів.
Таким чином правдива динамічна поведінка взаємодіючих фаз моделюється при їх збагаченні флотації. Комп'ютерні коди розвинені в середовищі Дельфи-3. Моделювання поведінки двовимірного комплексу впродовж сотень тисяч циклів, які містять сотні часток, може бути закінчено за прийнятний період часу завдяки засобам об'єктного програмування.
3.2. Перевірка працездатності чисельної моделі і налаштування її параметрів
Перед використанням описаної вище чисельної моделі для дослідження процесу взаємодії вугільних часток і повітряних бульбашок необхідно виконати перевірку правильності підібраних чинників з урахуванням властивостей фаз, що беруть участь, щоб модель адекватно відбивала реально протікаючі процеси. Для первинного налаштування моделі виконано моделювання відриву повітряної бульбашки від мінеральної пластинки. Цей експеримент комп'ютерного моделювання був проведений в умовах, відтворюючих фізичний експеримент[2].
Рівняння переміщення повітряної бульбашки уподовж похило розташованої пластинки в спрощеному виді:
mdv/dt = Fв·Sin α – Fc – f·(Fв - m·g)·Cos α, (7)
де m – маса бульбашки;
Fв – виштовхуюча сила;
Fc – сила опору переміщенню бульбашки, пов'язана з опором рідини і з силою, обумовленою взаємодією приповерхневих шарів гідратів бульбашки і пластинки;
f – коефіцієнт тертя.

Рисунок 3 - Схема сил, діючих на бульбашку при його переміщенні вздовж похилої пластинки
Масою бульбашки і силою його тяжіння можна нехтувати зважаючи на їх мале значення в порівнянні з іншими діючими силами.
Для виконання досліджень скляна пластинка готувалася таким чином. На поверхню пластинки наклеювався тонкий шар вугільного порошку. Потім повітряна бульбашка контактувала з цією пластинкою, зануреною у воду, і прикріплялася до сторони з наклеєними вугільними частинками. Після цього пластинка поступово нахилялася до тих пір, поки бульбашка повітря не відривалася від пластинки і не спливала. Кут нахилу пластинки, при якому відбувається відрив бульбашки від її поверхні, вважається критичним. За величиною критичного кута нахилу пластинки судять про активність флотації мінералу, що вивчається, шар якого наклеєний на поверхні пластинки.
У комп'ютерній моделі поверхня пластинки з наклеєним на неї вугільним порошком моделювалася набором дрібних вугільних часток, які були міцно прикріплені одна до іншої за допомогою підбору коефіцієнтів нормальної деформації. Результати моделювання представлені в графічній формі на рис. 4.

Рисунок 4 - Комп'ютерні фрагменти дослідження руху повітряної бульбашки від дна кювети вздовж пластинки в перебігу 1 300 000 циклів
На рис. 4 показані кінцеві фрагменти комп'ютерних фільмів після закінчення 1.3 c (1 300 000 циклів). Один цикл моделювання відповідав 10-6 з реального часу експерименту. Модель дає можливість простежити практично на кожному циклі рахунку зміна положення координат центру тяжіння усіх елементів, радіусу бульбашки, його швидкість. Бульбашка мала діаметр 2 мм і стійко закріплювався на пластинці при її нахилі до 50 (рис. 4, а).
В процесі моделювання було помічено, що бульбашка при переміщенні уздовж пластинки обертається навколо своєї осі. Це було визначено по зміні положення радіусу бульбашки. При цьому бульбашка дещо деформувалася і витягувалася уздовж пластинки, формуючи 5 елементарних контактів з її поверхнею. Точки контакту збільшують міцність з'єднання бульбашки з поверхнею пластинки і бульбашку залишається прикріпленим до пластинки.
При нахилі пластинки до кута в 15° відбувається просування бульбашки повітря вперед і вгору, до іншого кінця пластинки (рис. 4, б). Проте швидкість переміщення бульбашки залишалася незначною - за 1.3 з бульбашка перемістилася на відстань близько 29мм, тобто бульбашка рухалася з середньою швидкістю 22 мм/с.
При куті нахилу пластинки рівному 25° бульбашка за цей же час долала відстань близько 90мм, переміщаючись уздовж пластинки (см. рис. 4, в). Таким чином, середня швидкість переміщення бульбашки за заданих початкових умов склала близько 69 мм/с.
При завданні кута нахилу пластинки рівним 55° спостерігалося швидке переміщення бульбашки уздовж поверхні усієї пластинки, його відрив і подальше різке спливання (рис. 4, г).
Отримані значення свідчать про те, що для гідрофільної поверхні швидкість переміщення бульбашки збільшується. Швидше просування бульбашки уздовж пластинки при збільшенні кута її нахилу викликане збільшенням результуючої сили, яка значно перевищує сили опору руху спливаючої бульбашки.
У роботі [3] приведені дані аналогічного експерименту, виконаного для спливання повітряних бульбашок уздовж похилої пластинки з органічного скла і сталевої.
За даними практики оптимальна швидкість переміщення газоподібної фази для бульбашок крупності флотації складає 50-150 мм/с при кутах нахилу пластинок в межах 25-55 градусів.
Таким чином, проведене моделювання продемонструвало прийнятну поведінку комп'ютерної моделі при моделюванні окремих стадій процесу взаємодії фаз при збагаченні флотації і довело її ефективність.
4. ДОСЛІДЖЕННЯ ВПЛИВУ КУТА ЗІТКНЕННЯ З ЧАСТИНКОЮ НА ТРАЄКТОРІЮ РУХУ ПОВІТРЯНОЇ БУЛЬБАШКИ
Для можливості якісного порівняння результатів імітаційного моделювання і натурного експерименту було виконано комп'ютерне моделювання закріплення частинки на бульбашці для наступних умов. Вугільна частинка діаметром 0.29 мм падала із швидкістю 0.3 мм/з на повітряну бульбашку діаметром 2 мм, що спливав із швидкістю 12 мм/с. Точка зустрічі зміщувалася відносно центру бульбашки на 100, 200, 300, 400, 500, 600, 700, 800, 900 і 1000 мікрон. Це зміщення може бути розглянуте як ексцентриситет відносно центру і напряму сили тяжіння. Початкова модель представлена на рис. 5.

Рисунок 5 - Початкова модель
Тут показані: x0 - X0 = e - ексцентриситет при зустрічі частинки і бульбашки, φ0 і φi - початковий кут торкання частинки і поточний, відповідно; R і r - положення радіусу бульбашки і частинки, відповідно; L - дуговий шлях центру тяжіння частинки; а також координати центрів тяжіння бульбашки і частинки.
Процес взаємодії частинки, що падає, і спливаючої вгору бульбашки моделювався впродовж 80000 циклів. Один цикл рахунку відповідав 10-6натурального часу.
Координати центрів тяжіння елементів і стан комплексу накопичувалися у вихідному файлі кожні 200 циклів. Для розрахунків прийнята взаємодія повітряної бульбашки діаметром 2.5мм (2000 пікселів) і вугільної частинки розміром 0.36мм (290 мкм) сферичної форми.
Дослідження, проведені раніше із застосуванням комп'ютерного моделювання, дозволили встановити, що при зіткненні повітряної бульбашки і мінеральної частинки тангенціальна компонента швидкості частинки зростає зі збільшенням ексцентриситету між центром бульбашки і точкою зустрічі з частинкою. Саме ця компонента швидкості при збільшенні до критичного значення викликає прослизання частинки відносно поверхні бульбашки і у результаті її відрив.
Крім того, певний інтерес представляють інші параметри переміщення частинки відносно бульбашки і комплексу в цілому.
На рис. 6 представлені розрахункові графіки траєкторій переміщення центру тяжіння частинки без урахування спливання бульбашки.

Рисунок 6 - Траєкторія центру ваги частинки без урахування спливання бульбашки при різних ексцентриситетах зіткнення
Вертикальні лінії на рис. 6 відповідають траєкторії руху частинки до зіткнення з бульбашкою. При утворенні агрегату флотації частинка закріплюється на бульбашці і рухається по його поверхні або разом з ним. Потім відбувається відрив частинки при ексцентриситеті зустрічі 100 і 1000 пікселів, тобто 125 і 1250 мкм або при вугіллі зіткнення від 5 до 65°.
Таким чином, проведені дослідження кінетики взаємодії фаз при флотаційного збагачення шляхом комп'ютерного моделювання та порівняння результатів розрахунку і експериментів показали прийнятну збіжність.
Як випливає з даних, максимальний час існування комплексу флотації та спільного руху частинки і бульбашки спостерігається при мінімальному значенні кута зіткнення.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- Гарковенко Е.Е. Взаємодія фаз при обезводненні тонких класів вугілля // Збагачення корисних копалин. Дніпропетровськ. - 2001. - №13(54). - с. 116-121.
- Ємельянов Д.С. Основи флотації вугілля. - Харків: ХГУ, 1958. - 290 c.
- Гарковенко Е.Е., Назимко Е.И., Самойлов А.И., Папушин Ю.Л. Особливості флотації і обезводнення тонкодисперсних вуглевмісних матеріалів. Донецьк: Норд-прес. - 2002. - 266 с.
- Гарковенко Е.Е., Назимко Е.И., Самойлов А.И и др. Особенности флотации и обезвоживания тонкодисперсных углесодержащих материалов. – Донецк: Норд-пресс. – 2002. – 256 с.
- S. S. Kim, B. I. Morsi, and S.–H. Chiang, Statistical Analysis of the Performance of a Selective Agglomeration Process Using n-heptane as Agglomerant, Coal Preparation, 15, 51-70 (1994).
- P. A. Cundall, O. D. L. Strack, A discrete numerical model for grannular assemblies, Geotechnique, 29:1, 47–65 (1979).
- Звягильский Е.Л. Изучение кинетики обрушения толщи над горизонтальными выработками мелкого заложения // Проблемы горного давления. – 1999. - № 2. – С. 17-29.
- Bruno M. S. et al. 1996. Some influences of saturation and fluid flow on sand production: Laboratory and Discrete Element Model Investigations. SPE 36534, Proc. 1996 SPE Ann. Tech. Conf., Denver, Colorado, 6–9 October, 447–461.
- O'Connor P.M., John R. Torczynski Dale S. Preece; Justin T. Klosek; John R. Williams Discrete Element Modeling of Sand Production Int. J. Rock Mech. & Min. Sci. 34:3–4, Paper No. 231.
- P. F. Whelan and D. J. Brown, Particle-Bubble Attachment in Froth Flotation, Bull. Inst. Min. a. Met., No 591, 593 (1956).
- Митрофанов С.И. Селективная флотация. М.: Металлургиздат. - 1958. – 726 с.
