Українська   English
ДонНТУ   Портал магистров

Реферат по теме выпускной работы

Содержание

Введение

Электропривод в современном понятии представляет собой сложную электромеханическую систему (ЭМС), для которой характерной особенностью является тесная взаимосвязь процессов в электрической и механической части. Наличие упругих звеньев механической части при взаимосвязи радикально изменяет свойства электропривода в целом и является причиной колебательных явлений в динамике. Колебательные составляющие движения электропривода приводят к отклонению переходных процессов от предписанных технологией и способствуют росту динамических нагрузок на электрическое и механическое оборудование.

Ограничение динамических нагрузок, точное воспроизведение заданных законов движения исполнительных органов машины являются фундаментальными задачами проектирования современного электропривода.

Обычно ограниченная жесткость связей между двигателем и исполнительным органом механизма, а иногда и между отдельными элементами механизма обусловлена конструктивными особенностями и требованиями уменьшения его массы и габаритов. Поэтому пожелания увеличить жесткость конструкции далеко не всегда могут быть выполнены.

Если к быстродействию автоматизированного электропривода не предъявляется высоких требований, а частота собственных упругих колебаний механизма достаточно велика, то влияние упругости связей на работу электропривода и характер движения исполнительного органа незначителен. При повышении требований к электроприводу, что почти всегда связано с необходимостью увеличения его быстродействия, упругость начинает влиять на работу установки. В системе возникают колебания, что приводит к повышенному износу, а иногда и поломке деталей, влияет на качество продукции и производительность механизма.

Одной из ЭМС, где упругие колебания оказывают негативный эффект на производительность механизма является электропривод мостового крана.

Для мостовых кранов с большой длиной пролета амплитуда упругих колебаний в направлении движения моста может достигать нескольких десятков миллиметров, что приводит к значительному увеличению механических напряжений в отдельных узлах конструкции и значительно сокращает срок ее службы за счет проявления усталости металла.

Вопрос горизонтальных колебаний балок мостового крана практически не затронут в литературе, несмотря на их широкое распространение и является актуальным направлением исследований.

1. Математическое описание объекта регулирования

В литературе достаточно много внимания уделено двухмассовым системам [1,2], на динамику которых в значительной степени влияет только одна частота собственных колебаний. Такую модель применяют к системам, в которых две большие массы связаны между собой упругой связью, массой которой пренебрегают.

Для случая, когда тележка, смещена относительно центральной точки моста, мост с тележкой можно представить в виде трехмассовой системы, структурная схема которой приведена на рис.1[3–5]. На рисунке 1 приняты такие обозначения: v1, v2, v3 — скорости точек, в которых расположены сосредоточенные массы m1, m2, m3; F1, F3 — усилия, создаваемые приводными двигателями колес; l — расстояние от крайней опоры до тележки; L — длина пролета; F12, F32 – упругие силы взаимодействия сосредоточенных масс, c12,c32 — коэффициенты упругости.

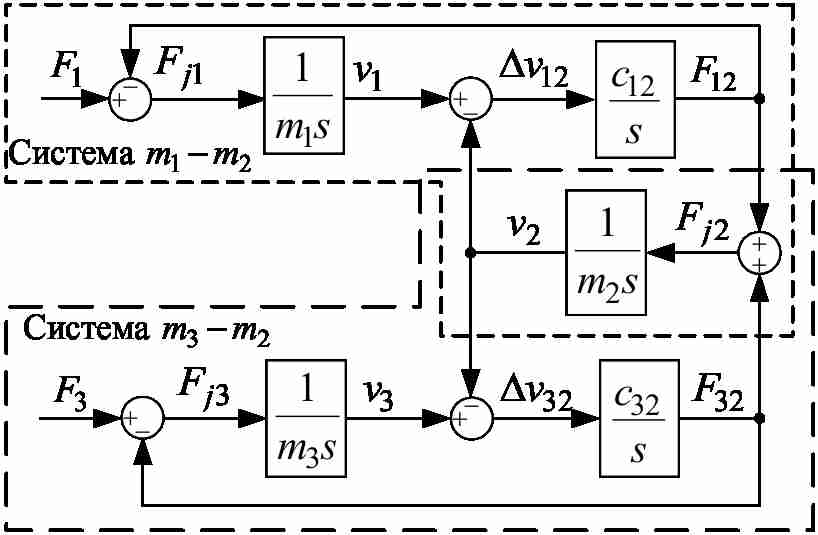
Структурная схема трёхмассовой системы

Рисунок 1 – Структурная схема трёхмассовой системы

Исследуем объект регулирования. Модель рис.1 имеет характеристический полином:

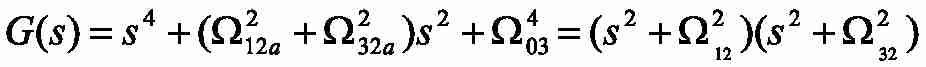
где

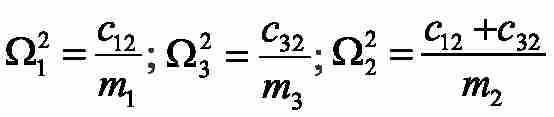
– частоты собственных колебаний движущихся масс;

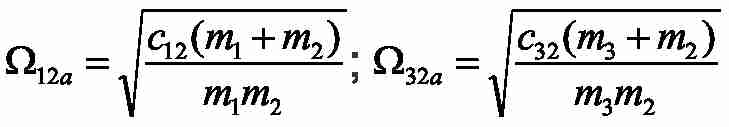
– частоты собственных упругих колебаний автономных двухмассовых систем с сосредоточенными массами m1-m2 и m3-m2;

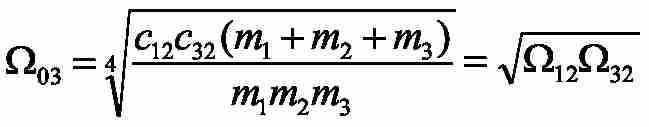
– среднегеометрический корень характеристического полинома рассматриваемой трехмассовой системы;

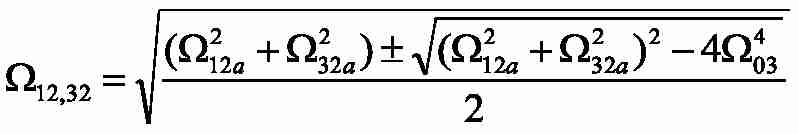
– частоты собственных упругих колебаний трехмассовой системы.

Передаточные функции (ПФ) от входных сил до динамического усилия, воздействующего на вторую массу, имеют вид:

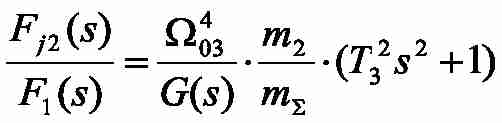
где

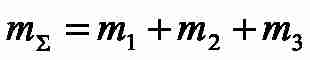
2. Синтез системы подчиненного регулирования скорости

В системе есть два электропривода, поэтому необходимо определить два коэффициента обратных связей и две постоянные времени регуляторов скорости. Структурная схема замкнутой системы регулирования приведена на рис.2.

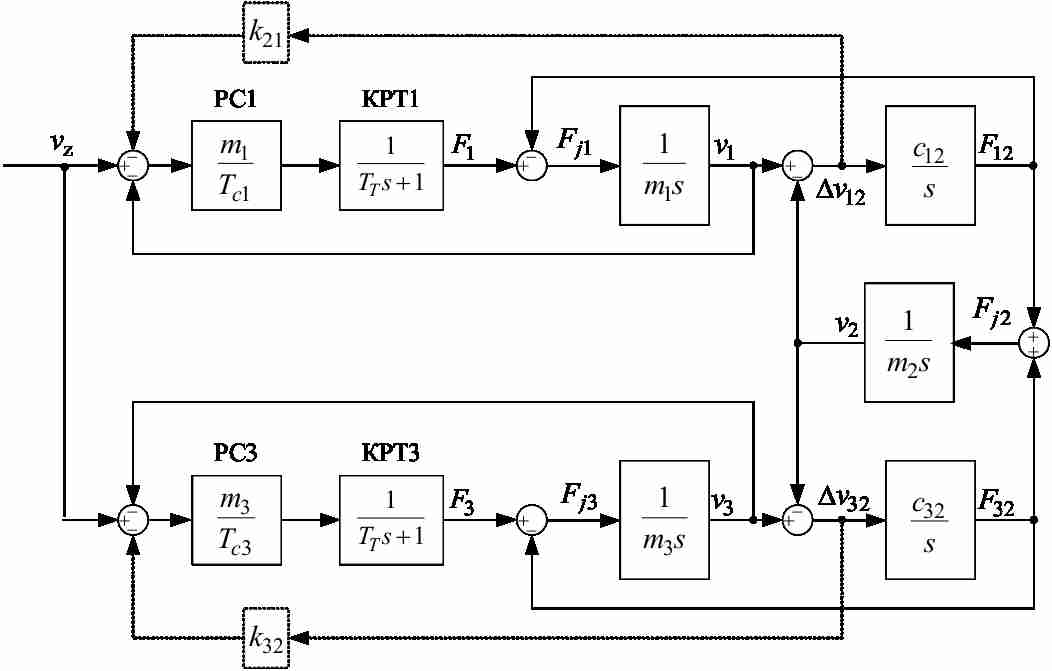
Структурная схема системы подчиненного регулирования скорости трехмассового объекта

Рисунок 2 – Структурная схема системы подчиненного регулирования скорости трехмассового объекта

Выполним оптимизацию замкнутых контуров скорости по модульному оптимуму. Для этого запишем передаточную функцию замкнутой системы от задания на скорость до скорости второй массы, которая имеет вид:

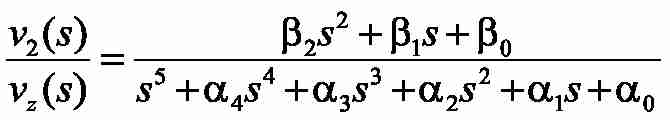
где:

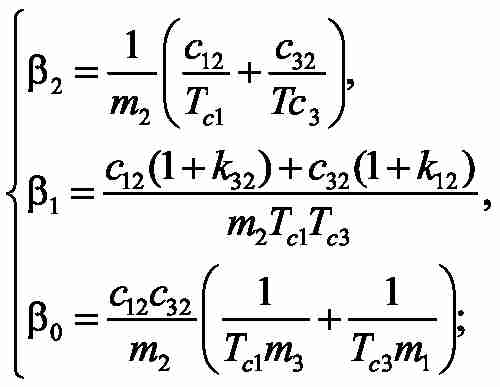
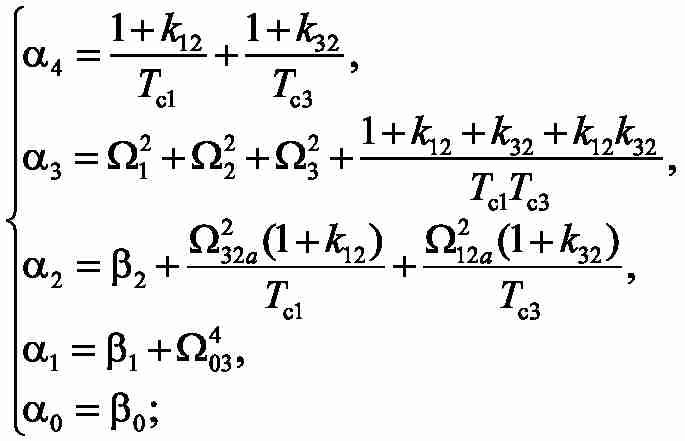
Для выведенной передаточной функции составляем уравнения, обеспечивающее достижение модульного оптимума. Чтобы определить как неизвестные постоянные времени Tc1,Tc3 , так и коэффициенты корректирующих обратных связей k12, k32, необходимо решить систему 4-х уравнений с 4-мя неизвестными:

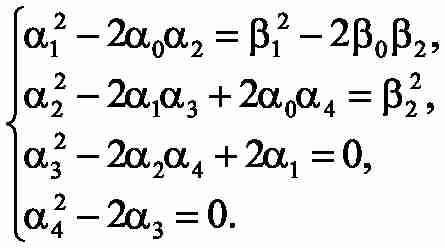
Решение данной системы уравнений выполняем численными методами. В качестве начальных приближений можно использовать значения постоянных времени и коэффициентов обратных связей, полученных при оптимизации автономных двухмассовых систем.

3. Результаты исследований

Исследуем процесс подавления упругих колебаний. Для этого примем следующие параметры объекта регулирования m1=m2=m3=20, c12=4000, и c32=2*c12. Результаты моделирования приведены на рис.3а. Параметры системы регулирования дополнительно рассчитаны для таких значений параметров: 1) m1=5кг, m2=m3=20кг, c32=2*c12; 2) m1=60кг, m2=m3=20кг, c32=2*c12. Результаты моделирования приведены на рис. 3б и 3в соответственно.

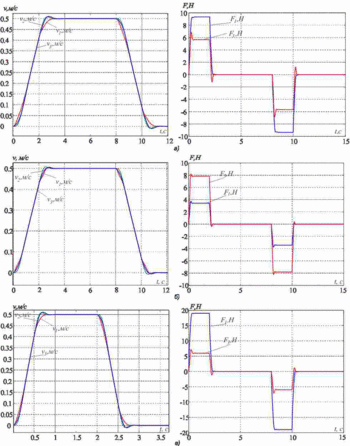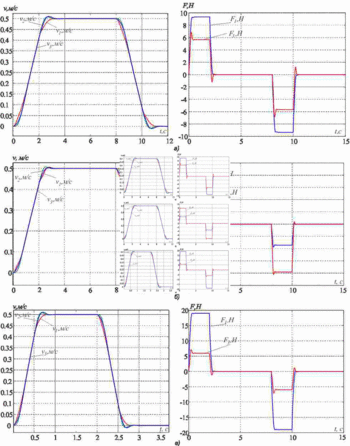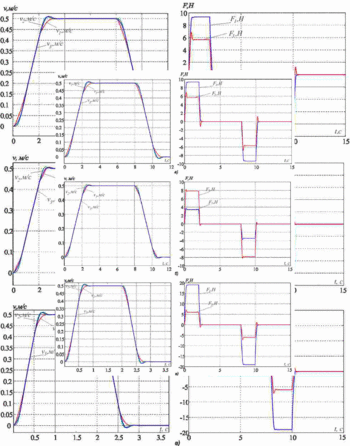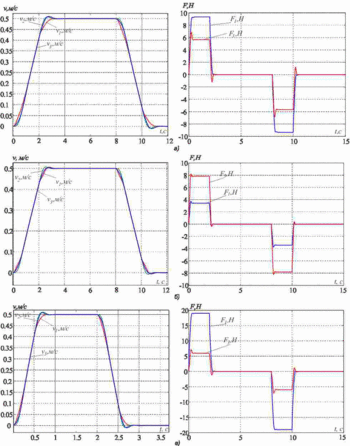
Переходные процессы в системе подчиненного регулирования

Рисунок 3 - Переходные процессы в системе подчиненного регулирования

(анимация: 6 кадров, 7 циклов повторения, 230 килобайт)

Видим, что во всех трёх случаях упругие колебания эффективно подавляются. Качество переходных процессов немного меняется, в сигналах приводных усилий и скоростей присутствует перерегулирование до 5-10%. Таким образом, можно сделать вывод, что предложенная методика позволяет эффективно подавлять упругие колебания в достаточно широком диапазоне соотношения движущихся масс и частот упругих колебаний.

Выводы

Применение корректирующих обратных связей по разностям скоростей движущихся масс позволяет эффективно подавлять упругие колебания в много-массовых системах. В зависимости от соотношения параметров исходной системы качество переходных процессов может немного ухудшаться, возможно увеличение перерегулирования или времени регулирования.

При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2015 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты. Эта часть реферата исключительно обзорная. Дальнейшая работа будет направлена на экспериментальное исследование и доработку имеющихся результатов в сфере цифровых систем управления.

Список источников

  1. Борцов Ю.А., Соколовский Г.Г. Автоматизированный электропривод с упругими связями. – СПб.: Энергоатомиздат, 1992. – 288 с.
  2. Коцегуб П.Х., Баринберг В.А., Толочко О.И., Федоряк Р.В. Оптимизация двухмассовых систем регулирования скорости // Известия вузов. Электроме-ханика. – 1998. – №4. – С. 54-57.
  3. Толочко О.И., Палис Ф., Бажутин Д.В. Гашение горизонтальных упругих колебаний конструкции мостового крана / О.И. Толочко, Ф. Палис, Д.В. Бажутин // Електромеханічні і енергозберігаючі системи. Тематичний випуск «Проблеми автоматизованого електропривода. Теорія і практика» - Кременчук: КрНУ, 2012. – Вип. 3/2012 (19). – С. 336-339.
  4. Палис Ф, Толочко О.И., Бажутин Д.В. Анализ поперечных колебаний мостового крана при изменении положения тележки / Ф. Палис, О.И. Толочко, Д.В. Бажутин // Вісник Національного технічного університету «Харківський політехнічний інститут». – Харків: НТУ «ХПІ», 2013, №36 (1009). – С. 36-39.
  5. O. Tolochko, D. Bazhutin. Suppression of horizontal structural vibration of overhead crane in transversal direction given fixed trolley position // Науково-технічний журнал «Електротехнічні та комп’ютерні системи», 2013. - вип. 12(88). – с.14-22.
  6. Борцов Ю. А. Автоматизированный электропривод с упругими связями / Ю. А. Борцов, Г. Г. Соколовский – СПб. : Энергоатомиздат, 1992. – 288 с.
  7. Коцегуб П. Х. Оптимизация двухмассовых систем регулирования скорости / П. Х. Коцегуб, В. А. Баринберг, О. И. Толочко, Р. В. Федоряк // Известия вузов. Электромеханика. – 1998. – №4. – С. 54 – 57.