Реферат за темою випускної роботи
Зміст
- Вступ
- 1. Математичний опис об'єкта регулювання
- 2. Синтез системи підпорядкованого регулювання швидкості
- 3. Результати досліджень
- Висновки
- Перелік посилань
Вступ
Електропривод в сучасному понятті являє собою складну електромеханічну систему (ЕМС), для якої характерною особливістю є тісний взаємозв'язок процесів в електричної і механічної частини. Наявність пружних ланок механічної частини при взаємозв'язку радикально змінює властивості електропривода в цілому і є причиною коливальних явищ у динаміці. Коливальні складові руху електроприводу призводять до відхилення перехідних процесів від запропонованих технологією і сприяють зростанню динамічних навантажень на електричне та механічне обладнання.
Обмеження динамічних навантажень, точне відтворення заданих законів руху виконавчих органів машини є фундаментальними завданнями проектування сучасного електроприводу.
Зазвичай обмежена жорсткість зв'язків між двигуном і виконавчим органом механізму, а іноді і між окремими елементами механізму обумовлена конструктивними особливостями і вимогами зменшення його маси і габаритів. Тому побажання збільшити жорсткість конструкції далеко не завжди можуть бути виконані.
Якщо до швидкодії автоматизованого електроприводу не пред'являється високих вимог, а частота власних пружних коливань механізму досить велика, то вплив пружності зв'язків на роботу електроприводу і характер руху виконавчого органу незначний. При підвищенні вимог до електроприводу, що майже завжди пов'язане з необхідністю збільшення його швидкодії, пружність починає впливати на роботу установки. В системі виникають коливання, що призводить до підвищеного зносу, а іноді і поломки деталей, впливає на якість продукції і продуктивність механізму.
Однією з ЕМС, де пружні коливання роблять негативний ефект на продуктивність механізму є електропривод мостового крана.
Для мостових кранів з великою довжиною прольоту амплітуда пружних коливань в напрямку руху моста може досягати декількох десятків міліметрів, що призводить до значного збільшення механічної напруги в окремих вузлах конструкції і значно скорочує термін її служби за рахунок прояву втоми металу.
Питання горизонтальних коливань балок мостового крана практично не є вивченим в літературі, незважаючи на їх широке розповсюдження і є актуальним напрямком досліджень.
1. Математичний опис об'єкта регулювання
У літературі досить багато уваги приділено двохмасовим системам [1, 2], на динаміку яких значною мірою впливає тільки одна частота власних коливань. Таку модель застосовують до систем, в яких дві великі маси пов'язані між собою пружною зв'язком, масою якої нехтують.
Для випадку, коли візок, є зміщеним відносно центральної точки моста, міст з візком можна представити у вигляді трихмасової системи, структурна схема якої наведена на рис.1 [3–5]. На малюнку 1 прийняті такі позначення: v1, v2, v3 - швидкості точок, в яких розташовані зосереджені маси m1, m2, m3; F1, F3 – зусилля, створювані приводними двигунами коліс; l – відстань від крайньої опори до візка; L – довжина прольоту; F12, F32 – пружні сили взаємодії зосереджених мас, c12,c32 – коефіцієнти пружності.
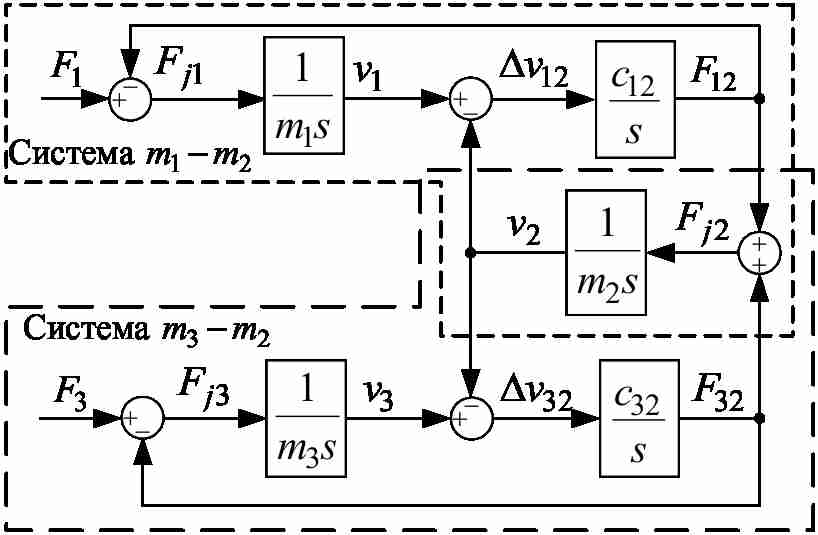
Рисунок 1 – Структурна схема трихмасової системи
Дослідимо об'єкт регулювання. Модель рис.1 має характеристичний поліном:
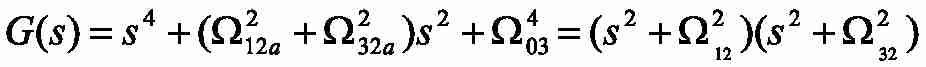
где
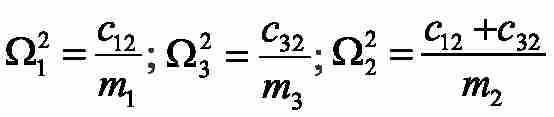
- частоти власних коливань рухомих мас;
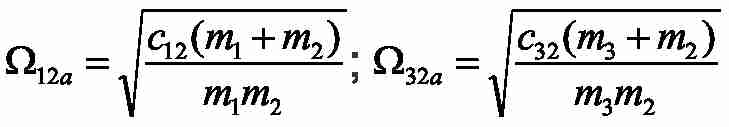
– частоти власних пружних коливань автономних двомасових систем із зосередженими масами m1-m2 и m3-m2;
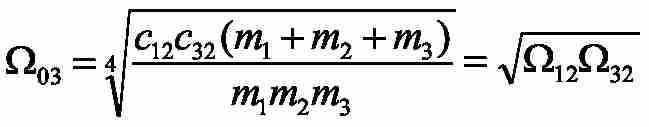
– середньогеометричний корінь характеристичного полінома розглянутої трихмасової системи;
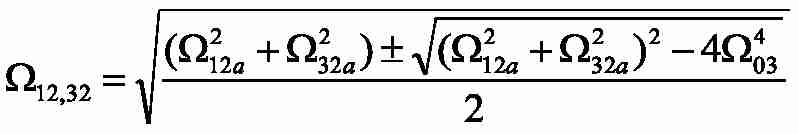
– частоти власних пружних коливань трехмассовой системи.
Передавальні функції (ПФ) від вхідних сил до динамічного зусилля, що впливає на другу масу, мають вигляд:
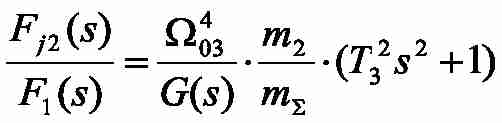
где
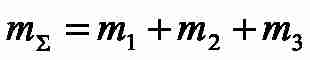
2. Синтез системи підпорядкованого регулювання швидкості
У системі є два електроприводи, тому необхідно визначити два коефіцієнти зворотних зв'язків і дві постійні часу регуляторів швидкості. Структурна схема замкнутої системи регулювання приведена на рис.2.
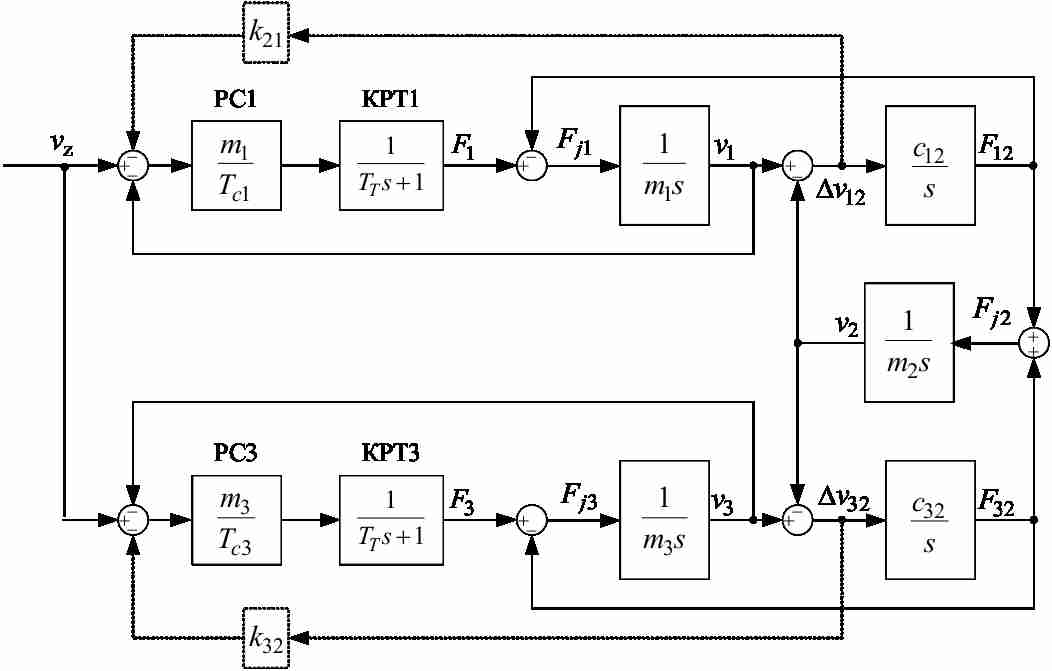
Рисунок 2 – Структурна схема системи підлеглого регулювання швидкості тримасового об'єкта
Виконаємо оптимізацію замкнутих контурів швидкості за модульним оптимумом. Для цього запишемо передавальну функцію замкненої системи від завдання на швидкість до швидкості другий маси, яка має вигляд:
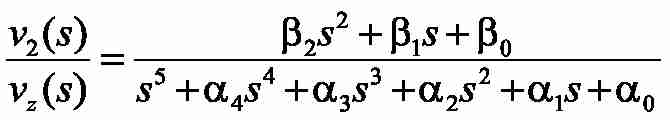
где:
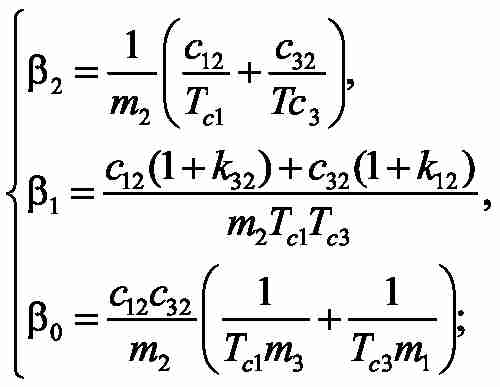
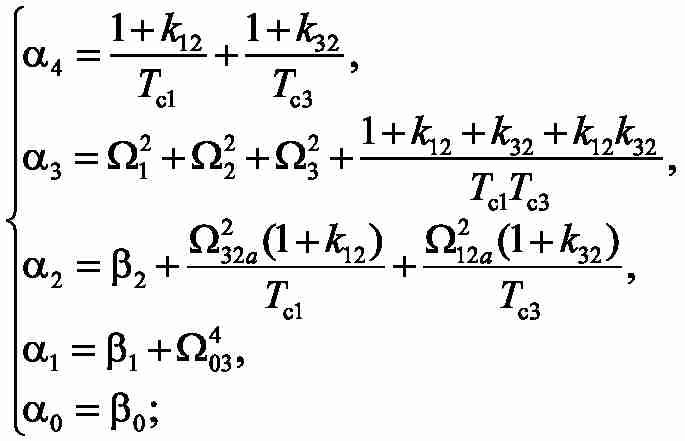
Для виведеної передавальної функції складаємо рівняння, що забезпечує досягнення модульного оптимуму. Щоб визначити як невідомі постійні часу Tc1,Tc3 , так і коефіцієнти коригувальних зворотних зв'язків k12, k32, необхідно вирішити систему 4-х рівнянь з 4-ма невідомими:
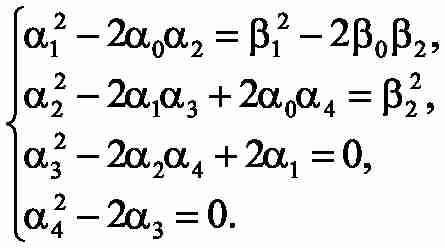
Рішення даної системи рівнянь виконуємо чисельними методами. В якості початкових наближень можна використовувати значення постійних часу і коефіцієнтів зворотних зв'язків, отриманих при оптимізації автономних двомасових систем.
3. Результати досліджень
Дослідимо процес придушення пружних коливань. Для цього приймемо наступні параметри об'єкта регулювання m1=m2=m3=20, c12=4000, и c32=2*c12. Результати моделювання наведені на рис.3а. Параметри системи регулювання додатково розраховані для таких значень параметрів: 1) m1=5кг, m2=m3=20кг, c32=2*c12; 2) m1=60кг, m2=m3=20кг, c32=2*c12. Результати моделювання наведені на рис. 3б і 3в відповідно.
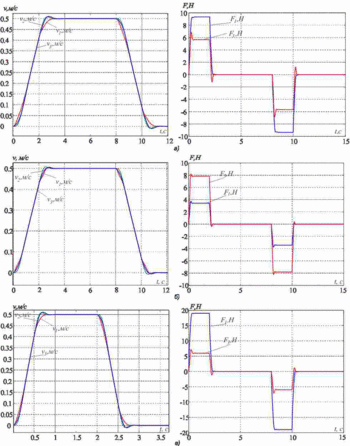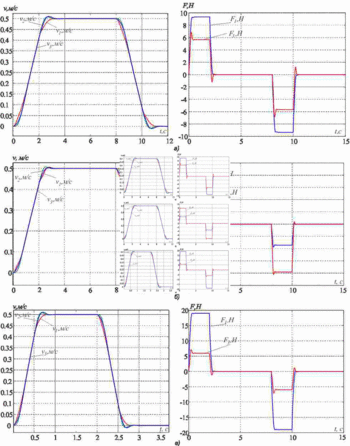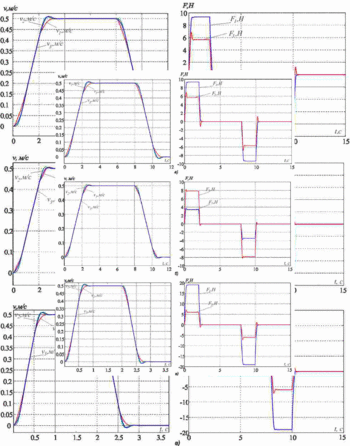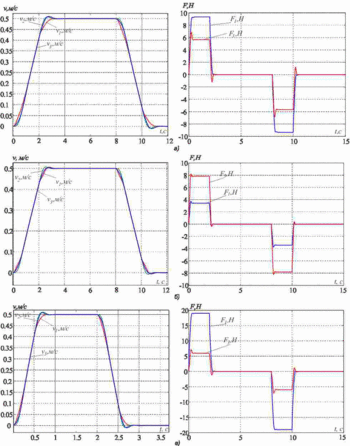
Рисунок 3 - Перехідні процеси в системі підпорядкованого регулювання
(анімація: 6 кадрів, 7 циклов повторення, 230 кілобайт)
Бачимо, що у всіх трьох випадках пружні коливання ефективно придушуються. Якість перехідних процесів трохи змінюється, в сигналах приводних зусиль і швидкостей присутній перерегулирование до 5-10%. Таким чином, можна зробити висновок, що запропонована методика дозволяє ефективно пригнічувати пружні коливання в досить широкому діапазоні співвідношення рухомих мас і частот пружних коливань.
Висновки
Застосування коригувальних зворотних зв'язків по різницям швидкостей рухомих мас дозволяє ефективно пригнічувати пружні коливання в багатомасових системах. Залежно від співвідношення параметрів вихідної системи якість перехідних процесів може трохи погіршуватися, можливе збільшення перерегулирования або часу регулювання.
При написанні цього реферату магистреская робота ще не завершена. Остаточне завершення: грудень 2015 року. Повний текст роботи і матеріали по темі можуть бути отримані у автора або його керівника після вказаної дати. Ця частина реферату виключно оглядова. Подальша робота буде спрямована на эксперементальное дослідження і доопрацювання наявних результатів у сфері цифрових систем керування.
Перелік посилань
- Борцов Ю.А., Соколовский Г.Г. Автоматизированный электропривод с упругими связями. – СПб.: Энергоатомиздат, 1992. – 288 с.
- Коцегуб П.Х., Баринберг В.А., Толочко О.И., Федоряк Р.В. Оптимизация двухмассовых систем регулирования скорости // Известия вузов. Электроме-ханика. – 1998. – №4. – С. 54-57.
- Толочко О.И., Палис Ф., Бажутин Д.В. Гашение горизонтальных упругих колебаний конструкции мостового крана / О.И. Толочко, Ф. Палис, Д.В. Бажутин // Електромеханічні і енергозберігаючі системи. Тематичний випуск «Проблеми автоматизованого електропривода. Теорія і практика» - Кременчук: КрНУ, 2012. – Вип. 3/2012 (19). – С. 336-339.
- Палис Ф, Толочко О.И., Бажутин Д.В. Анализ поперечных колебаний мостового крана при изменении положения тележки / Ф. Палис, О.И. Толочко, Д.В. Бажутин // Вісник Національного технічного університету «Харківський політехнічний інститут». – Харків: НТУ «ХПІ», 2013, №36 (1009). – С. 36-39.
- O. Tolochko, D. Bazhutin. Suppression of horizontal structural vibration of overhead crane in transversal direction given fixed trolley position // Науково-технічний журнал «Електротехнічні та комп’ютерні системи», 2013. - вип. 12(88). – с.14-22.
- Борцов Ю. А. Автоматизированный электропривод с упругими связями / Ю. А. Борцов, Г. Г. Соколовский – СПб. : Энергоатомиздат, 1992. – 288 с.
- Коцегуб П. Х. Оптимизация двухмассовых систем регулирования скорости / П. Х. Коцегуб, В. А. Баринберг, О. И. Толочко, Р. В. Федоряк // Известия вузов. Электромеханика. – 1998. – №4. – С. 54 – 57.
