Реферат по теме выпускной работы
Содержание
- Введение
- 1. Актуальность темы
- 2. Цель и задачи исследования, планируемые результаты
- 3. Научная новизна
- 4. Основные определения
- 5. Обзор исследований и разработок
- 5.1 Исследование графов
- 5.2 Базовый алгоритм распознавания графов коллективом агентов
- 5.3 Модификации базового алгоритма распознавания
- 5.4 Детерминированная разметка вершин графа
- Выводы
- Список источников
Введение
В современном мире роботы всё больше приобретают огромную роль во всех сферах человеческой деятельности: используют в медицине, сфере обслуживания, военном деле, при проведении спасательных операций. Развитие робототехники не стоит на месте и постоянно идет по пути увеличения операций, которые должны выполнять роботы без участия человека. Это говорит о сложности решения задач управления роботов. Поэтому актуальной проблемой в области разработки программного обеспечения мобильных роботов является проблема распознавания графа коллективом агентов.
В настоящее время существует большое количество различного рода сред, требующих изучения. Исследование среды – это своего рода дискретная система, представленная как модель взаимодействия управляющей и управляемой систем, взаимодействие которых зачастую представляется как процесс перемещения управляющего автомата по графу управляемой системы. В данной работе моделью исследования роботов является конечный связный неориентированный граф.
Исследованию графа при помощи одного агента посвящено много работ, при этом остается малоисследованно распознавание графа при помощи нескольких блуждающих по нему агентов. Это делает актуальной задачу исследования графа при помощи нескольких блуждающих по нему агентов.
Если агентов несколько, то один может блокировать движение другого. Проблема недопущения такого блокирования оказалась трудной, важной и далёкой от разрешения.
1. Актуальность темы
При распознавании графа несколькими блуждающими по нему агентами актуальной задачей является проблема эффективности взаимодействия роботов. Требуется разработать такой алгоритм движения, при котором агент-экспериментатор ищет кратчайший путь для одного из агентов-исследователей учитывая движения второго агента-исследователя.
Данная магистерская работа посвящена актуальной задачи создания маршрутов движения агентов по неизвестному графу, сбору и обработки информации о графе и способы построения графа по этой информации.
В качестве базовой информации используется алгоритм Грунский И.С, Стёпкин А.В. – «Алгоритм распознавания конечных неориентированных графов коллективом агентов».
2. Цель и задачи исследования, планируемые результаты
Целью исследования является предложить алгоритм распознавания графа коллективом агентов, в котором агенты-исследователи не простаивают, если еще граф распознан не полностью. Для этого агент-экспериментатор ищет кратчайший путь для одного агента-исследователя через территорию распознанную вторым агентом-исследователем.
Основные задачи исследования:
1. Изучить основные определения и обозначения теории графов.
2. Изучить режимы работы исследования графа
3. Разработка улучшенного метода и алгоритма распознавания графа коллективом агентов
4. Оценка работы алгоритма на разных типах графа
Объект исследования: процесс перемещения агентов по неориентированному графу.
Предмет исследования: метод распознавания графа коллективом агентом, который заключается в том, что агент-экспериментатор ищет кратчайший путь для одного агента-исследователя через территорию распознанную вторым агентом-исследователем.
3. Научная новизна
Научная новизна заключается в предложенной модификации базового алгоритма распознавания графа коллективом агентов при помощи трех мобильных агентов (два исследователя и один экспериментатор), использовании четырёх красок. Распознавание проводится путем обхода графа в ширину и идентификацией ребер с помощью «инциденторов».
4. Основные определения
Рассмотрим используемые понятия и определения для того, чтобы иметь точное представление об исследуемой среде. Дискретная система – кибернетическая система, все элементы которой, а также связи между ними (т.е обращающаяся в системе информация) имеют дискретный характер [9].
Исследование среды – это в некотором роде дискретная система, представленная как модель взаимодействия управляющей и управляемой систем (управляющего автомата и операционной среды), взаимодействие которых зачастую представляется как процесс перемещения управляющего автомата по графу управляемой системы.
Теория графов – раздел дискретной математики, изучающий свойства графов. В общем смысле граф представляется как множество вершин (узлов), соединённых рёбрами. В строгом определении графом называется такая пара множеств. G=(V, E), где V есть подмножество любого счётного множества, а E – подмножество V×V.
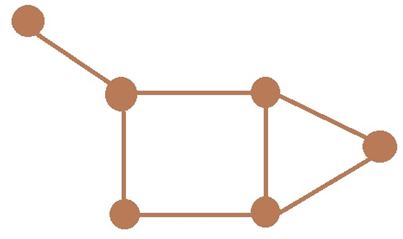
Рисунок 1.1 – Граф с шестью вершинами и семью ребрами
Инцидентор – место соединения вершины и ребра (обычно используются парой – инцидентор от начальной вершины и инцидентор у конечной вершины).
Матрица инцидентности – одна из форм представления графа, в которой указываются связи между инцидентными элементами графа (ребро(дуга) и вершина).
Столбцы матрицы соответствуют ребрам, строки – вершинам. Ненулевое значение в ячейке матрицы указывает
связь между вершиной и ребром (их инцидентность). В случае ориентированного графа каждой дуге
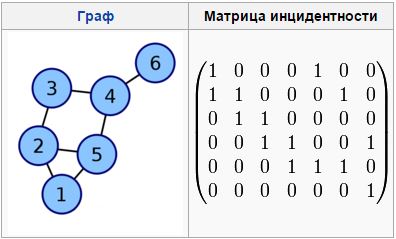
Рисунок 1.2 – Матрица инцидентности для заданного графа
Инцидентор – место соединения вершины и ребра.
Коллектив агентов – совокупность агентов, исследующих граф.
Агент исследователь – агент, который ходит по среде и размечает вершины, одновременно передавая информацию агенту-экспериментатору.
Агент экспериментатор – агент, который восстанавливает граф по данным, переданным агентами исследователями.
Поиск в глубину – один из методов обхода графа. Стратегия поиска в глубину, как и следует из названия, состоит в том, чтобы идти «вглубь» графа, насколько это возможно. Алгоритм поиска описывается рекурсивно: перебираем все исходящие из рассматриваемой вершины рёбра. Если ребро ведёт в вершину, которая не была рассмотрена ранее, то запускаем алгоритм от этой нерассмотренной вершины, а после возвращаемся и продолжаем перебирать рёбра.
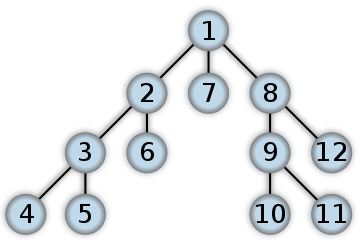
Рисунок 1.3 – Порядок обхода дерева в глубину
Изоморфизм графа. В теории графов изоморфизмом графов G=(VG,EG) и H=(VH,EH) называется биекция между множествами вершин графов f: VG→VH такая, что любые две вершины u и v графа G смежны тогда и только тогда, когда вершины f(u) и f(v) смежны в графе H. Здесь графы понимаются неориентированными и не имеющими весов вершин и ребер. В случае, если понятие изоморфизма применяется к ориентированным или взвешенным графам, накладываются дополнительные ограничения на сохранение ориентации дуг и значений весов. Если изоморфизм графов установлен, они называются изоморфными и обозначаются как G≈H.
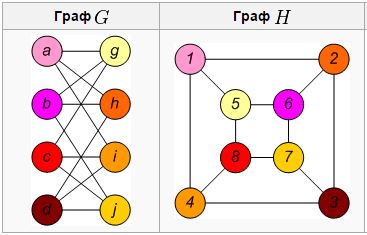
Рисунок 1.4 – Два изоморфных графа
Перешеек – вершина, в которой встречаются агенты исследователи.
Матрица смежности – это квадратная матрица A размера n, в которой значение элемента aij равно числу рёбер из i-й вершины графа в j-ю вершину.
Петля – ребро, начало и конец которого находятся в одной и той же вершине.
Висячая вершина – вершина называется висячей если имеет степень единица [9].
5. Обзор исследований и разработок
5.1 Исследование графов
Началом исследования поведения автоматов в лабиринтах принято считать работу К. Шенона 1951 года, в которой рассматривалась задача поиска автоматом-мышью заданной цели в лабиринте. Иным источником данного направления можно считать вычислительные системы с внешней памятью в виде плоскости или пространства П.Фишера. Активное изучение поведения автоматов в лабиринтах начинается в 1971 году после появления работ К. Деппа описывающих обход шахматных лабиринтов конечными автоматами.
В дальнейшем Г.Дудеком проводились исследования в области анализа свойств неизвестной среды при различных способах взаимодействия автомата с операционной средой, а также при различной априорной информации о ней. Анализ графа включает в себя ряд частных задач, основными из которых есть: проблема самолокализации (определения вершины графа, в которой первоначально находиться автомат), проблема контроля карты (проверки изоморфизма исследуемого графа и графа-эталона (карты)) и проблема полного распознавания графа.
В работе И.С.Грунского и Е.А. Татаринова предложен метод распознавания графа одним агентом, базирующийся на стратегии поиска в глубину. Начиная с 1993 года Г.Дудек публикует работы по исследованию графов роем агентов. Алгоритм работы роя заключается в следующем: все агенты (память агента должна быть такой, чтобы могла вместить карту всего графа) начинают работу с одной вершины; договорившись заранее о времени следующей встречи, они делят доступные ребра между собой и расходятся по ним; обходят о пределенную часть графа и возвращаются в исходную вершину для объединения полученных карт; договариваются о следующей встрече и снова расходятся и так продолжается до полного распознавания.
Исследованию графа при помощи одного агента посвящено много работ, получено множество результатов о возможности и сложности такого распознавания. При этом остается малоисследованно распознавание графа коллективом блуждающих по нему агентов. Это делает актуальной задачу проведения систематического исследования экспериментов по распознаванию графа несколькими блуждающими по нему агентами, то есть создания маршрутов движения агентов по неизвестному графу, разметки его элементов, сбора и обработки локальной информации о графе и способов построения графа по этой информации, с точностью до отметок на элементах графа [7].
5.2 Базовый алгоритм распознавания графов коллективом агентов
Для создания нумерации вершин, существуют множество различных способов. Но, учитывая то, что агенты могут перемещаться из одной вершины в другую только по ребру, соединяющему эти вершины, то целесообразно использовать нумерацию, для построения которой агенты совершат минимальное количество переходов по ребрам графа G.
При обходе агентами графа в глубину, каждой вершине ставится в соответствие номер по порядку (неявно). В процессе обхода посещенные вершины, у которых восстановлены не все инцидентные им ребра образуют простые, непересекающиеся пути. Каждый из этих путей может быть однозначно пройден агентом, построившим этот путь, в прямом и обратном направлении.
Рассмотрим базовый алгоритм распознавания графов коллективом агентов с использованием неявной прямой нумерации вершин.
Вход: граф G неизвестный агентам-исследователям и агенту-экспериментатору, все элементы графа G окрашены краской w, агент A помещен в произвольную вершину v.
Выход: все элементы графа G.
Данные: v – вершина графа G, в которой находится агент.
Алгоритм основан на стратегии поиска в глубину, которая заключается в следующем: агенты идут «в глубину», пока это возможно, потом возвращаются назад, в поисках другого пути с еще не посещенными вершинами и не пройденными ребрами. В случае обнаружения смежной вершины, окрашенной в чужой цвет, агент метит все перешейки из текущей вершины в чужую область и сообщает второму АИ, через агента-экспериментатора, о необходимости распознавания помеченных перешейков. Пока второй АИ распознает перешейки, первый АИ не может метить новые перешейки. В случае отсутствия других возможных вариантов перемещения, кроме как пометить новый перешеек, первый АИ останавливается до того момента, пока второй АИ не распознает все помеченные перешейки [1].
Для решения поставленной задачи предлагается следующая стратегия:
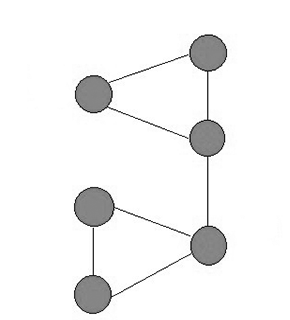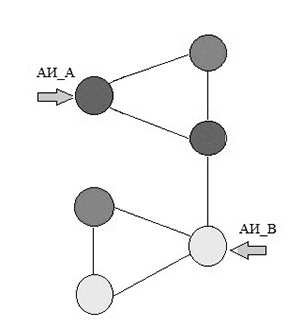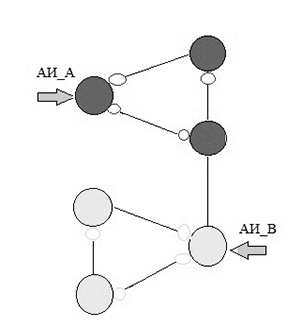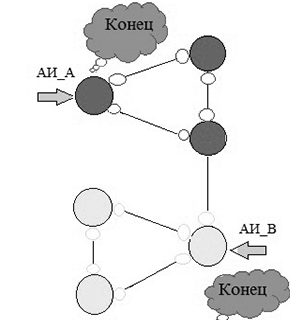
Рисунок 2 – Работа агентов исследователей
(анимация: объем – 126 КБайт, количество кадров – 11, размер – 320х325)
Предлагаемая стратегия имеет ряд отличительных свойств:
1) распознаваемый граф G не известен агентам.
2) агенты на каждом шаге могут обладать информацией только о метках элементов из окрестности Q(v) текущей вершины v
3) при посещении вершин графа G агенты создают неявную нумерацию пройденных вершин: при первом посещении вершины она окрашивается агентом А в красный цвет (агентом B в желтый цвет) и ей фактически ставится в соответствие номер, равный значению переменной Сч_А (Сч_B в случае агента B).
Отметим, что переменные Cч_А и Сч_В принимают соответственно нечетные и четные значения. На основе этой нумерации и происходит восстановление графа G, путем построения изоморфного ему графа H. В процессе обхода агенты строят неявные деревья обхода в глубину и относительно этих деревьев все ребра разделяются на три вида: древесные – ребра, принадлежащие деревьям и окрашиваемые при первом прохождении по ним в красный (желтый) цвет; обратные – ребра, соединяющие вершины одного дерева, но не принадлежащие самому дереву и окрашиваемые при первом прохождении в черный цвет; перешейки – ребра, которые соединяют деревья обхода разных агентов. Древесные ребра проходятся по крайней мере 2 раза и при последнем проходе окрашиваются агентами в черный цвет. Обратные проходятся каждым агентом по два раза: первый, прошедший по нему, агент метит перешеек, окрашивая его в красный (агент А) или в желтый (агент В) цвет, второй, прошедший по нему, агент распознает перешеек и красит его в черный цвет.
Красные (желтые) вершины графа G , на каждом шаге алгоритма, образуют красный (желтый) если это не возврат для распознания перешейков) – укорачивается, при распознавании обратного ребра и перешейков – не изменяется. Вершина, у которой все инцидентные ребра распознаны, окрашивается в черный цвет. Алгоритм заканчивает работу, когда красный и желтый пути становятся пустыми, а все вершины черными.
Предложен базовый метод восстановления ранее неизвестного графа с точностью до меток на элементах графов, при помощи передвигающегося по нему агента.
Базовый метод допускает модификации, которые позволяют получить лучшую оценку временной сложности и упрощают агента, который передвигается по графу, однако, накладывают дополнительные ограничения на восстанавливаемый граф.
5.3 Модификации базового алгоритма распознавания
Первая модификация базового алгоритма распознавания. Первая модификация базового алгоритма состоит в следующем: агенты – исследователи помещаются в различные вершины графа G, эти вершины сразу окрашиваются в красный и желтый цвета для агентов A и B соответственно. Агенты-исследователи передвигаются одновременно, пошагово передавая агенту-экспериментатору информацию, агент-экспериментатор, в свою очередь, обрабатывает полученные от них данные на основе которых и строит граф H изоморфный графу G с точностью до отметок на графе [7].
Вторая модификация базового алгоритма распознавания. Вторая модификация базового алгоритма направлена на оптимизацию процедур распознавания обратных ребер и перешейков, а также работы агентов. Что, в конечном итоге, позволило на порядок снизить верхнюю оценку временной, коммуникационной сложностей алгоритма и числа переходов по ребрам, совершаемых агентами-исследователями, а также позволило избавиться от зависимости памяти агентов-исследователей от числа вершин распознаваемого графа. Это дало возможность использовать одних и тех же агентов для распознавания любого графа из рассматриваемого множества [7].
Третья модификация базового алгоритма распознавания. В предыдущих модификациях агенты-исследователи взаимодействуют между собой исключительно за счет окраски элементов графа, что позволяет значительно снизить коммуникационную сложность алгоритма. В третьей модификации базового алгоритма распознавания агентам-исследователям добавлена возможность вписывать номера непосредственно в вершину, а также увеличена, по сравнению с предыдущими модификациями, память агентов-исследователей. Это дало возможность снизить временную сложность выполнения алгоритма с O(n³) до O(n²), числа переходов по ребрам, совершаемых агентами-исследователями с O(n³) до O(n), а коммуникационной сложности с O(n³) до O(n²×log(n²)). Емкостная сложность при этом осталась неизменной [7].
5.4 Детерминированная разметка вершин графа
Задача разметки вершин конечного простого связного неорграфа осуществляется посредством блуждающего по нему агента. Разметка производится за один проход так, что в окрестности каждой вершины все вершины размечены разными метками. Задача построения Д-разметки формулируется следующим образом. Агент устанавливается в произвольную вершину априори неизвестного ему графа, все вершины которого помечены одной и той же меткой. Агент должен осуществить Д-разметку вершин этого графа, причём если вершина уже помечена агентом, то её метка в дальнейшем не изменяется. Построение минимальной Д-разметки на основе только локальной информации о вершинах графа представляется в общем случае невозможным. Поэтому в работе рассматривается построение «жадных» алгоритмов разметки. Показано, что с помощью Д-разметки агент может восстановить исследуемый граф с точностью до изоморфизма и что минимальная Д-разметка восстановленного графа может быть получена применением к его транзитивному замыканию известных в теории графов алгоритмов правильной раскраски. Метод Д-разметки вершин агентом A3 основан на обходе графа в ширину. При этом для неявного именования вершин используются метки путей в них из начальной вершины по дереву обхода. Разработан соответствующий полиномиальный алгоритм. Увеличение размера наблюдаемой агентом окрестности (т. е. объёма его входной информации) приводит к увеличению сложности робота, который реализует функции агента, поэтому целесообразно рассмотреть модель с ограничениями на размер наблюдения [5].
Выводы
Проведен обзор и анализ существующих алгоритмов по распознаванию графа коллективом агентов. В результате были выявлены основные достоинства и недостатки анализируемых алгоритмов. Изучены основные определения и понятия.
Большая роль в анализе существующих алгоритмов была отведена базовому алгоритму. В данном алгоритме каждый агент-исследователь использует две различные краски. В этом алгоритме впервые, наряду с временной T(n), емкостной S(n) сложностями и числом переходов по ребрам, совершаемых агентами-исследователями, исследуется коммуникационная сложность K(n) – сложность, определяемая количеством сообщений, которыми нужно обменяться агентам-исследователям с агентом-экспериментатором для распознавания графа.
Рассмотрены также модификации базового алгоритма, образующие спектр алгоритмов распознавания, основанных на методе обхода графа в глубину, с распознаванием обратных ребер и ребер перешейков.
Список источников
- Стёпкин А.В. Использование коллектива агентов для распознавания графа// Компьютерные исследования и моделирования. – 2013. – №4. – С. 525-532.
- Стёпкин А.В.Распознавание конечных неориентированных графов коллективом агентов // Журнал обчислювальної та прикладної математики. – 2013. – №2(112). – С. 161-168.
- Грунский И.С., Татаринов Е.А. Распознавание конечного графа блуждающим по нему агентом // Прикладная дискретная математика. Приложение. Комбинаторный анализ. Теория графов. – 2009.– №1. – С. 492-496.
- Стёпкин А.В. Возможность и сложность распознавания графов тремя агентами // Таврический вестник информатики и математики. – 2012. – №1 (20). – C. 88–98.
- Грунский И.С., Сапунов С.В. Детерминированная разметка вершин графа блуждающим по нему агентом // Прикладная дискретная математика. Приложение. – 2012. – №5. – C. 89–91.
- Килибарда Г., Кудрявцев В. Б., Ушчумлич Щ. Независимые системы автоматов в лабиринтах // Дискретная математика. – 2003. – Т. 15, вып. 2. – С. 3–39.
- Стёпкин А.В. Распознавание графов с помощью коллектива агентов // Диссертация на соискание ученой степени кандидата физико-математических наук. – 2015. – С.1-185.
- Стёпкин А.В. Распознавание конечных графов тремя агентами // Искусственный интеллект. – 2011. – №2. – С. 84-93.
- Материал из свободной электронной библиотеки Википедия: словарь теории графов. Электронный ресурс. Режим доступа: http://ru.wikipedia.org/wiki/Глоссарий_теории_графов
- Кудрявцев В.Б., Алешин С.В., Подколзин А.С. Введение в теорию автоматов. – М.: Наука, 1985. – 320 с.
- Оре О. Теорія графів / Оре О. – М. : Наука, 1980. – 340 с.
Важное замечание
При написании данного автореферата магистерская работа еще не завершена. Предположительная дата завершения – 1 декабря 2015 г. Полный текст работы, а также материалы по теме могут быть получены у автора или его руководителя после указанной даты.
