Abstract
Сontents
- Introduction
- 1. Theme urgency
- 2. Goal and tasks of the research
- 3. Scientific novelty
- 4. Basic definitions
- 5. Review of the Research and Development
- 5.1 Study the graphs
- 5.2 The basic recognition algorithm graphs collective agents
- 5.3 Modifications to the basic recognition algorithm
- 5.4 Deterministic marking graph vertices
- Conclusion
- References
Introduction
In today's world, robots are increasingly becoming a huge role in all spheres of human activity are used in medicine, the service sector, military affairs, during the rescue operations. The development of robotics is not standing still and is constantly on the go ways to increase the operation to be performed by robots with no human intervention. This suggests the complexity of solving the robot control. Therefore, an urgent problem in the area of software development of mobile robots is the issue of recognition of the collective count agents.
Currently, there are many different kinds of environments that require study. The study environment – a kind of a discrete system is presented as a model of interaction between the management and control systems whose interaction is often presented as a process of moving the machine control the graph of the control system. In this paper we study a model of robots is a finite connected undirected graph.
Research graph with a single agent in many papers, thus remains unexplored recognition Count with a few wandering through it agents. This makes it urgent to study the graph with a few stray thereon agents.
If several agents, one can block the movement of another. The problem to avoid such blocking proved difficult, important and far from resolution.
1. Theme urgency
In recognition of the graph multiple agents wandering on it an urgent problem is the problem of the efficiency of interaction robotov. Trebuetsya develop an algorithm of motion in which the experimenter is looking for an agent shortcut for one of the agents of researchers taking into account the movement of the second agent researcher.
This master's work is devoted to the urgent task of creating routes agents unknown to Count, gathering and processing information on a graph and how to construct a graph of this data.
As basic information algorithm Grunskii IS, Stёpkin AV – End-recognition algorithm
undirected graphs collective agents".
2. Goal and tasks of the research
The aim of this study is to propose an algorithm for recognizing graph collective agents, agents-which researchers are not idle, even if the count is not fully recognized. To this end, an experimental agent seeking the shortest path for a single-agent researchers through the recognized second agent-investigator.
The main objectives of the study:
1. To study the basic definitions and notations of graph theory.
2. To study the modes of study Count
3. Development of an improved method and recognition algorithm graph collective agents
4. Evaluation of the algorithm on different types of graph
The object of study: the process of moving agents undirected graph.
Subject of research: recognition method Count collective agent, who is the agent experimenter seeks the shortest path to a single agent, the researchers through the recognized second agent-investigator.
3. Scientific novelty
Scientific novely of the proposed modification is a basic recognition algoritnm graph collective agents with three mobile agents (two researchers and one experimenter) using four colors. Detection is performed by traversing the graph in width and with the help of proxy authentication ribs.
4. Basic definitions
Consider used concepts and definitions in order to have an accurate idea of the medium under study. Discrete system – cybernetic system, all of whose elements, as well as links between them (ie, contact the system information) have a discrete nature [9].
Study environment – is a kind of discrete system represented as a model of interaction between the management and control systems (control the machine and the operating environment), whose interaction is often presented as a process of moving control machine controlled by the Count system.
Graph theory – the section of discrete mathematics that studies the properties of graphs. In general terms, the graph is represented as a set of vertices (nodes) connected by edges. In the strict definition graph is a pair of sets. G = (V, E), where V is a subset of any countable set, and E – a subset of V×V.
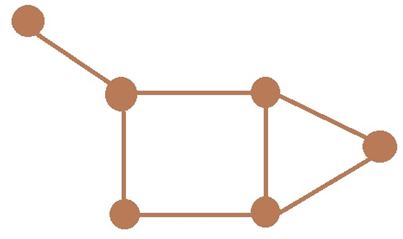
Figure 1.1 – A graph with six vertices and seven edges
Incidentors – the place of the vertices and edges (commonly used pair - incidentor from the initial vertex and incidentor at the end vertex).
The incidence matrix – one of the forms of representation of the graph, which makes the link between the incident to the elements of the graph (edge (arc) and top).
The columns correspond to the edges, the line – heights. A non-zero value in the cell of the matrix indicates
the connection between the top and the edge (of incidence). In case of a directed graph of each arc
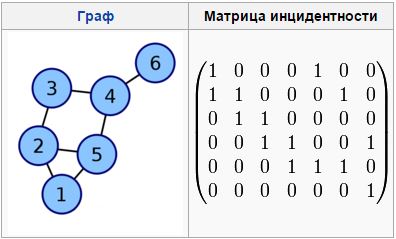
Figure 1.2 – The incidence matrix for a given graph
The team of agents – a set of agents investigating the graph.
Agent researcher – an agent that runs on Wednesdays and marks the top, at the same time passing information to the agent, the experimenter.
Agent experimenter – an agent that restores the graph of the data transmitted agents investigators.
Search in depth – one of the methods graph traversal. Search strategy in depth, as the name implies, is to go "deeper" graph as much as possible. The search algorithm is described recursively: enumerates all coming from the top of the ribs considered. If the edge leads to the summit, which was not considered previously, the ability to run on top of this unexamined, and then come back and continue fingering the edges.
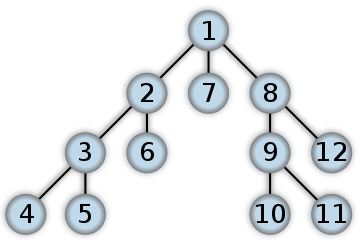
Figure 1.3 – The order of traversal depth
Graph isomorphism. In graph theory, graph isomorphism G = (VG, EG) and H = (VH, EH) is called a bijection between the set of vertices f: VG→VH such that any two vertices u and v of G are adjacent if and only if the vertex f (u) and f (v) adjacent in H. Here undirected graphs are understood and do not have weights of vertices and edges. If the concept is applied to the oriented isomorphism or a weighted graph, impose additional restrictions on the orientation of the arcs and the preservation of the values of the weights. If the graph isomorphism is set, they are said to be isomorphic, and are referred to as G≈H.
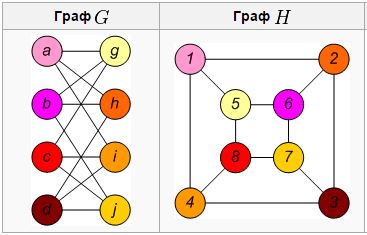
Figure 1.4 – Two isomorphic graph
Isthmus – the top, where there are agents of the researchers.
The adjacency matrix – a square matrix A of size n, wherein the value of the element aij is the number of edges of the i-th vertex in the j-th vertex.
Loop - an edge, the beginning and end of which are in the same top.
Hanging peak – peak it is called if the hanging has a unit [9].
5. Review of the Research and Development
5.1 Study the graphs
The beginning of the study of behavior of automata in labyrinths is considered to be the work of C. Shannon in 1951, which examined the problem of search automatic mouse-given purpose in a maze. Other sources of this area can be considered computing systems with external memory in the form plane or space P.Fishera. active study of the behavior of automata in labyrinths started in 1971 after the appearance of the works of K. Depp describing bypassing chess labyrinths finite automata.
Later G.Dudekom conducted research in the field of analyzing the properties of an unknown medium in different ways to interact with the machine operating environment, as well as different a priori information about it. An analysis of the graph includes a number of specific problems, most important of which is: the problem of self-localization (determining the vertex, which is initially in the machine), the problem of the control card (check the test graph isomorphism and graph-standard (map)) and the problem of the full recognition of the graph.
The paper I.S.Grunskogo and EA Tatarinov proposed a method of recognizing the graph one agent, based on the search strategy in depth. Since 1993 G.Dudek publishes work on the study of graphs swarm of agents. The algorithm of the swarm is as follows: all agents (memory agent must be such that the card could fit the entire graph) start with a single vertex; agreed in advance of the time of the next meeting, they share the available rib each other and disperse them; bypass certain part of the graph and return to the starting vertex for the association of the cards; They agree to meet again and again apart and so it goes to full recognition.
Research graph with a single agent in many papers, there were a lot of results on the opportunities and challenges of such recognition. This is uncharted recognition graph team wandering through it agents. This makes it urgent to carry out systematic research experiments on the recognition graph multiple agents wandering through it, that is the creation of routes agents unknown graph layout of its elements, the collection and processing of information on the local box and the methods of constructing the graph of this data, up to a level on the elements of the graph [7].
5.2 The basic recognition algorithm graphs collective agents
To create a numbering of the vertices, there are lots of different ways. But given the fact that the agents can move from one node to another only on the edge joining the top, it is advisable to use the numbering, for the construction of which the agents will make a minimum number of transitions on the edges of the graph G.
When crawling agents graph in depth, each vertex is associated with the number of order (implicitly). During bypass visited peaks that have not recovered all incident edges form a simple, non-intersecting path. Each of these pathways can be uniquely passed agent who built this way, in forward and reverse direction [1].
Consider a basic recognition algorithm counts with a team of agents implicit direct numbering of vertices.
Input: graph G is an unknown agent-agent researchers and experimenters, all the elements of G are colored paint w, agent A is placed in an arbitrary vertex v.
Output: all the elements of the graph G.
Details: v – vertex of G, which is the agent.
To solve this problem we propose the following strategy:
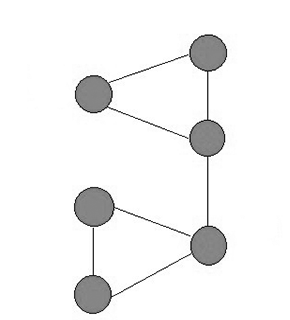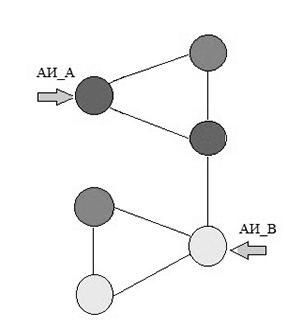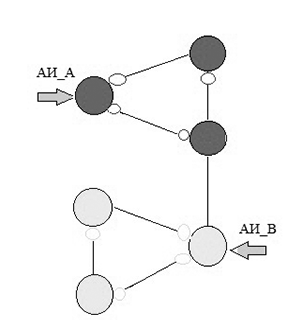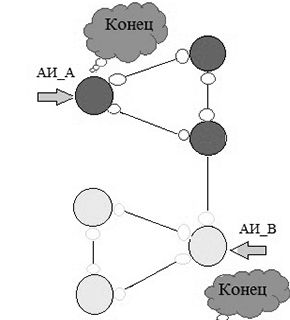
Figure 2 – The work of researchers agents
(animation: volume - 126 Kbytes, the number of frames - 11 size - 320х325)
The proposed strategy has a number of distinctive features:
1) recognize the graph G is not known agents.
2) agents at each step may have information only on the labels of elements from the neighborhood of Q (v) the current node v
3) when visiting the vertices of G agents create an implicit numbering passed peaks: the first visit to the top of it is a coloring agent A red (Agent B in yellow color) and it is actually assigned a number equal to the value of the variable Sch_A (Sch_B in the case of agent B ).
Note that the variables Cch_A and take Sch_V respectively odd and even values. On the basis of this numbering, and there is a restoration of the graph G, by constructing it isomorphic graph H. In the process of building a bypass agents implicit tree traversal in depth about these trees and all the edges are divided into three types: wood – rib belonging trees and stained at the first passage on the These red (yellow) color; back - edges connecting vertices of a tree, but do not belong to wood and stained at the first passage in the black; necks - ribs which connect the tree traversal different agents. Wood ribs extend at least 2 times, and the last passage of coloring agents in black. The reverse takes place every agent twice: the first, the last of him, the agent marks the isthmus, coloring it red (agent A) or yellow (Agent B) color, and the second, held on it, the agent detects the isthmus and color it black.
Red (yellow) vertices of G, at each step of the algorithm to form red (yellow) if it does not return for the recognition of the isthmus) – shortened when recognizing return ribs and necks - does not change. The top, in which all the edges incident to be recognized, to be painted in black. The algorithm terminates when the red and yellow path are empty, and all the black tops.
A basic method of restoring a previously unknown count up to the mark on the cell counts, using it to move around the agent.
The basic method allows modifications that allow to obtain a better estimate of the time complexity and simplify the agent that moves the graph, however, impose additional restrictions on restored graph.
5.3 Modifications to the basic recognition algorithm
The first modification of the basic recognition algorithm. The first modification of the basic algorithm is as follows: agents – researchers are placed in different vertices of G, these vertices once painted in red and yellow colors for the agents A and B, respectively. Agents researchers move simultaneously incrementally transferring agent experimenter information agent experimenter, in turn, processes the data received from them on the basis of which builds a graph H isomorphic to the graph G up to the marks on the graph [7].
The second modification of the basic recognition algorithm. The second modification of the basic algorithm is aimed at optimizing recognition procedures back edges and necks, as well as the agents. What, ultimately, helped by an order to reduce the upper estimate of the time of communication complexity of the algorithm and the number of transitions in the ribs made by agents, investigators, and it will get rid of the memory of agents depending on the number of researchers recognizable peaks of the graph. This made it possible to use the same agents for the detection of any graph of the set in question [7].
The third modification of the basic recognition algorithm. In previous versions of agent researchers interact solely through color graph elements that can significantly reduce the communication complexity of the algorithm. In the third modification of the basic recognition algorithm agents, the researchers added the possibility to enter a number directly into the top, and increased compared to previous modifications, the memory agents and researchers. This made it possible to reduce the time complexity of the algorithm with O(n³) to O(n²), the number of transitions in the ribs made by agents, researchers with the O(n³) to O(n), and communication complexity O(n³) to O ( n²×log(n²)). Space complexity remains unchanged [7].
5.4 Deterministic marking graph vertices
The task of marking the final vertex simple connected neorgrafa performed by wandering through it the agent. The marking is done in one pass, so that in the vicinity of each vertex of all vertices are marked by different labels.
The task of building the D-mark is as follows. The agent is installed in an arbitrary vertex of the graph priori unknown to him, all the vertices are labeled the same label. The agent must carry out D-marking peaks of the graph, with the tip if the agent is already marked, the mark it does not change in the future.
Building A minimum markup on the basis only of local information on the tops of the graphite is generally impossible. Therefore, in the paper the construction of the "greedy" algorithms markup. It is shown that with the help of the D-mark agent can restore the analyzed graph with up to isomorphism and the minimum D-counting of reduced graph can be obtained by applying to its transitive closure known in graph theory algorithms proper coloring.
Method D-marking peaks agent A3 is based on graph traversal wide. At the same time for implicit naming of vertices used tags in their ways from the initial vertex of the tree traversal. Develop appropriate polynomial algorithm.
Increasing the size of the observable agent surroundings (ie. E. The volume of its input data) increases the complexity of the robot, which implements the functions of an agent, so it is advisable to consider a model with restrictions on the size of the observation [5].
Conclusion
The review and analysis of existing algorithms for recognizing graph collective agents. As a result, we identified the main strengths and weaknesses of the analyzed algorithms. We studied the basic definitions and concepts.
A major role in the analysis of existing algorithms was given a basic algorithms. In this algorithm, each agent uses a researcher two different paints. In this algorithm, first, along with the time T(n), capacitive S(n) complexity and number of transitions in the ribs, committed by agents researchers studied communication complexity K(n)- the complexity of determining the amount reported post to exchange agents, researchers with an experimental agent to recognize count.
Also considered modifying the basic algorithm, which form the spectrum of pattern recognition algorithms based on graph traversal method in depth, with the recognition of edges and back edges necks.
References
- Стёпкин А.В. Использование коллектива агентов для распознавания графа// Компьютерные исследования и моделирования. – 2013. – №4. – С. 525-532.
- Стёпкин А.В.Распознавание конечных неориентированных графов коллективом агентов // Журнал обчислювальної та прикладної математики. – 2013. – №2(112). – С. 161-168.
- Грунский И.С., Татаринов Е.А. Распознавание конечного графа блуждающим по нему агентом // Прикладная дискретная математика. Приложение. Комбинаторный анализ. Теория графов. – 2009.– №1. – С. 492-496.
- Стёпкин А.В. Возможность и сложность распознавания графов тремя агентами // Таврический вестник информатики и математики. – 2012. – №1 (20). – C. 88–98.
- Грунский И.С., Сапунов С.В. Детерминированная разметка вершин графа блуждающим по нему агентом // Прикладная дискретная математика. Приложение. – 2012. – №5. – C. 89–91.
- Килибарда Г., Кудрявцев В. Б., Ушчумлич Щ. Независимые системы автоматов в лабиринтах // Дискретная математика. – 2003. – Т. 15, вып. 2. – С. 3–39.
- Стёпкин А.В. Распознавание графов с помощью коллектива агентов // Диссертация на соискание ученой степени кандидата физико-математических наук. – 2015. – С.1-185.
- Стёпкин А.В. Распознавание конечных графов тремя агентами // Искусственный интеллект. – 2011. – №2. – С. 84-93.
- Материал из свободной электронной библиотеки Википедия: словарь теории графов. Электронный ресурс. Режим доступа: http://ru.wikipedia.org/wiki/Глоссарий_теории_графов
- Кудрявцев В.Б., Алешин С.В., Подколзин А.С. Введение в теорию автоматов. – М.: Наука, 1985. – 320 с.
- Оре О. Теорія графів / Оре О. – М. : Наука, 1980. – 340 с.
Important note
When writing this master's work is not yet complete. Possible completion date – December 1, 2015. Full text of work and materials on the topic can be obtained from the author or his head after that date.
