Реферат за темою випускної роботи
Зміст
- Вступ
- 1. Актуальність теми
- 2. Мета і завдання дослідження, плановані результати
- 3. Наукова новизна
- 4. Основні визначення
- 5. Огляд досліджень і розробок
- 5.1 Дослідження графів
- 5.2 Базовий алгоритм розпізнавання графів колективом агентів
- 5.3 Модифікації базового алгоритму розпізнавання
- 5.4 Детермінована розмітка вершин графа
- Висновки
- Список джерел
Вступ
У сучасному світі роботи все більше набувають величезну роль у всіх сферах людської діяльності: використовують в медицині, сфері обслуговування, військовій справі, при проведенні рятувальних операцій. Розвиток робототехніки не стоїть на місці і постійно йде по шляху збільшення операцій, які повинні виконувати роботи без участі людини. Це говорить про складність вирішення завдань управління роботів. Тому актуальною проблемою в області розробки програмного забезпечення мобільних роботів є проблема розпізнавання графа колективом агентів.
В даний час існує велика кількість різного роду середовищ, які потребують вивчення. Дослідження середовища – це свого роду дискретна система, представлена як модель взаємодії керуючої і керованої систем, взаємодія яких часто представляється як процес переміщення керуючого автомата по графу керованої системи. У даній роботі моделлю дослідження роботів є кінцевий зв'язний неорієнтовані граф.
Дослідженню графа за допомогою одного агента присвячено багато робіт, при цьому залишається малодослідженим розпізнавання графа за допомогою декількох блукаючих по ньому агентів. Це робить актуальним завдання дослідження графа за допомогою декількох блукаючих по ньому агентів.
Якщо агентів кілька, то один може блокувати рух іншого. Проблема недопущення такого блокування виявилася важкою, важливою і далекою від дозволу.
1. Актуальність теми
При розпізнаванні графа декількома блукаючими по ньому агентами актуальним завданням є проблема ефективності взаємодії роботів. Потрібно розробити такий алгоритм руху, при якому агент-експериментатор шукає найкоротший шлях для одного з агентів-дослідників враховуючи руху другого агента-дослідника.
Дана магістерська робота присвячена актуальній задачі створення маршрутів руху агентів по невідомому графу, збору та обробки інформації про графа і способи побудови графа за цією інформацією.
В якості базової інформації використовується алгоритм Грунський І.С, Стёпкін А.В. – Алгоритм розпізнавання кінцевих неорієнтованих
графів колективом агентів
.
2. Мета і завдання дослідження, плановані результати
Метою дослідження є запропонувати алгоритм розпізнавання графа колективом агентів, в якому агенти-дослідники не простоюють, якщо ще граф розпізнаний не повністю. Для цього агент-експериментатор шукає найкоротший шлях для одного агента-дослідника через територію розпізнану другим агентом-дослідником.
Основні завдання дослідження:
1. Вивчити основні визначення та позначення теорії графів.
2. Вивчити режими роботи дослідження графа
3. Розробка поліпшеного методу і алгоритму розпізнавання графа колективом агентів
4. Оцінка роботи алгоритму на різних типах графа
Об'єкт дослідження: процес переміщення агентів з неорієнтованого графу.
Предмет дослідження: метод розпізнавання графа колективом агентом, який полягає в тому, що агент-експериментатор шукає найкоротший шлях для одного агента-дослідника через територію розпізнану другим агентом-дослідником.
3. Наукова новизна
Наукова новизна полягає в запропонованій модифікації базового алгоритму розпізнавання графа колективом агентів за допомогою трьох мобільних агентів (два дослідника і один експериментатор), використанні чотирьох фарб. Розпізнавання проводиться шляхом обходу графа в ширину і индентифікацієй ребер за допомогою інцінденторов.
4. Основні визначення
Розглянемо використовувані поняття і визначення для того, щоб мати точне уявлення про досліджуваному середовищі.
Дискретна система – кібернетична система, всі елементи якої, а також зв'язки між ними (тобто обращающаяся в системі інформація) мають дискретний характер [9].
Дослідження середовища – це в деякому роді дискретна система, представлена як модель взаємодії керуючої і керованої систем (керуючого автомата і операційного середовища), взаємодія яких часто представляється як процес переміщення керуючого автомата по графу керованої системи.
Теорія графів – розділ дискретної математики, що вивчає властивості графів. У загальному значенні граф представляється як безліч вершин (вузлів), з'єднаних ребрами. У строгому визначенні графом називається така пара множин. G = (V, E), де V є підмножина будь-якого рахункового безлічі, а E – підмножина V×V.
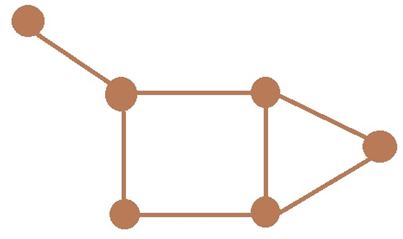
Рисунок 1.1 – Граф з шістьма вершинами і сім'ю ребрами
Інцідентор – місце з'єднання вершини і ребра (зазвичай використовуються парою - інцідентор від початкової вершини і інцідентор у кінцевої вершини).
Матриця інцидентності – одна з форм представлення графа, в якій зазначаються зв'язку
між інцидентними елементами графа (ребро (дуга) і вершина). Стовпці матриці відповідають ребрам, рядки – вершин. Нульове значення в осередку матриці вказує зв'язок між вершиною і ребром (їх инцидентность).
У разі орієнтованого графа кожній дузі
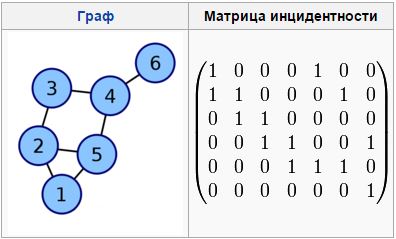
Рисунок 1.2 – Матриця інцидентності для заданого графа
Колектив агентів – сукупність агентів, які досліджують граф.
Агент дослідник – агент, який ходить по середовищу і розмічає вершини, одночасно передаючи інформацію агенту-експериментатору.
Агент експериментатор – агент, який відновлює граф за даними, переданим агентами дослідниками.
Пошук в глибину – один з методів обходу графа. Стратегія пошуку в глибину, як і випливає з назви, полягає в тому, щоб іти «вглиб» графа, наскільки це можливо. Алгоритм пошуку описується рекурсивно: перебираємо всі вихідні з розглянутої вершини ребра. Якщо ребро веде в вершину, яка не була розглянута раніше, то запускаємо алгоритм від цієї нерозглянутих вершини, а після повертаємося і продовжуємо перебирати ребра.
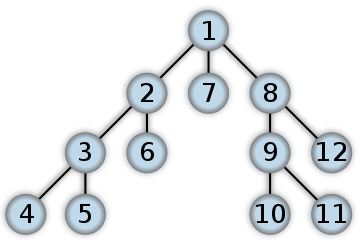
Рисунок 1.3 – Порядок обходу дерева в глибину
Ізоморфізм графа. У теорії графів изоморфизмом графів G =(VG, EG) і H = (VH, EH) називається біекція між множинами вершин графів f:VG→VH така, що будь-які дві вершини u і v графа G суміжні тоді і тільки тоді, коли вершини f(u) і f(v) суміжні в графі H. Тут графи розуміються неорієнтованими і не мають ваг вершин і ребер. У випадку, якщо поняття ізоморфізму застосовується до орієнтованим або зваженим графам, накладаються додаткові обмеження на збереження орієнтації дуг і значень ваг. Якщо ізоморфізм графів встановлений, вони називаються ізоморфними і позначаються як G≈H.
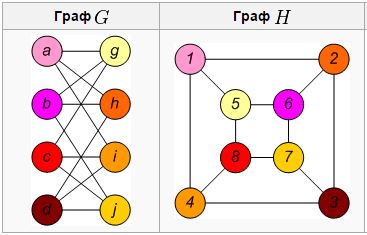
Рисунок 1.4 - Два ізоморфних графа
Перешийок – вершина, в якій зустрічаються агенти дослідники.
Матриця суміжності – це квадратна матриця A розміру n, в якій значення елемента aij дорівнює числу ребер з i-й вершини графа в j-ю вершину.
Петля – ребро, початок і кінець якого знаходяться в одній і тій же вершині.
Висяча вершина – вершина називається висячої якщо має ступінь одиниця [9].
5. Огляд досліджень і розробок
5.1 Дослідження графів
Початком дослідження поведінки автоматів в лабіринтах прийнято вважати роботу К. Шенона 1951, в якій розглядалася задача пошуку автоматом-мишею заданої мети в лабіринті. Іншим джерелом даного напрямку можна вважати обчислювальні системи із зовнішньою пам'яттю у вигляді площини або простору П. Фішера. Активне вивчення поведінки автоматів в лабіринтах починається в 1971 році після появи робіт К. Деппа описують обхід шахових лабіринтів кінцевими автоматами
Надалі Г.Дудеком проводилися дослідження в галузі аналізу властивостей невідомої середовища при різних способах взаємодії автомата з операційним середовищем, а також при різній апріорної інформації про неї. Аналіз графа включає в себе ряд приватних завдань, основними з яких є: проблема самолокалізаціі (визначення вершини графа, в якій спочатку перебувати автомат), проблема контролю карти (перевірки ізоморфізму досліджуваного графа і графа-еталона (карти)) і проблема повного розпізнавання графа.
У роботі І.С.Грунского і Е.А. Татаринова запропонований метод розпізнавання графа одним агентом, який базується на стратегії пошуку в глибину. Починаючи з 1993 року Г.Дудек публікує роботи з дослідження графів роєм агентів. Алгоритм роботи рою полягає в наступному: всі агенти (пам'ять агента повинна бути такою, щоб могла вмістити карту всього графа) починають роботу з однієї вершини; домовившись заздалегідь про час наступної зустрічі, вони ділять доступні ребра між собою і розходяться по них; обходять певну частину графа і повертаються у вихідну вершину для об'єднання отриманих карт; домовляються про наступну зустріч і знову розходяться і так продовжується до повного розпізнавання.
Дослідженню графа за допомогою одного агента присвячено багато робіт, отримано безліч результатів про можливості та складності такого розпізнавання. При цьому залишається малодослідженим розпізнавання графа колективом блукаючих по ньому агентів. Це робить актуальним завдання проведення систематичного дослідження експериментів з розпізнавання графа декількома блукаючими по ньому агентами, тобто створення маршрутів руху агентів по невідомому графу, розмітки його елементів, збору і обробки локальної інформації про графа і способів побудови графа за цією інформацією, з точністю до відміток на елементах графа [7].
5.2 Базовий алгоритм розпізнавання графів колективом агентів
Для створення нумерації вершин, існують безліч різних способів. Але, враховуючи те, що агенти можуть переміщатися з однієї вершини в іншу тільки по ребру, що з'єднує ці вершини, то доцільно використовувати нумерацію, для побудови якої агенти здійснять мінімальну кількість переходів по ребрах графа G.
При обході агентами графа в глибину, кожній вершині ставиться у відповідність номер по порядку (неявно). У процесі обходу відвідані вершини, у яких відновлені не всі інцідентние їм ребра утворюють прості, непересічні шляху. Кожен з цих шляхів може бути однозначно пройдений агентом, побудував цей шлях, в прямому і зворотному напрямку.
Розглянемо базовий алгоритм розпізнавання графів колективом агентів з використанням неявній прямої нумерації вершин.
Вхід: граф G невідомий агентам-дослідникам і агенту-експериментатору, всі елементи графа G пофарбовані фарбою w, агент A поміщений в довільну вершину v.
Вихід: всі елементи графа G.
Дані: v – вершина графа G, в якій знаходиться агент.
Алгоритм заснований на стратегії пошуку в глибину, яка полягає в наступному: агенти йдуть «в глибину», поки це можливо, потім повертаються назад, у пошуках іншого шляху з ще не відвіданими вершинами і не пройденими ребрами. У разі виявлення суміжній вершини, пофарбованої в чужій колір, агент мітить все перешийки з поточної вершини в чужу область і повідомляє другу АІ, через агента-експериментатора, про необхідність розпізнавання помічених перешейков. Поки другий АІ розпізнає перешийки, перший АІ не може мітити нові перешийки. У разі відсутності інших можливих варіантів переміщення, окрім як помітити новий перешийок, перший АІ зупиняється до того моменту, поки другий АІ не може розпізнати всі помічені перешийки [1].
Для вирішення поставленого завдання пропонується наступна стратегія:
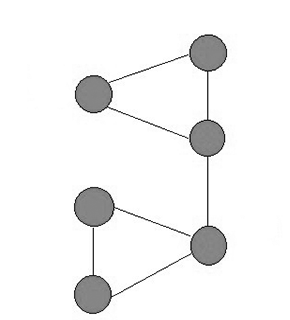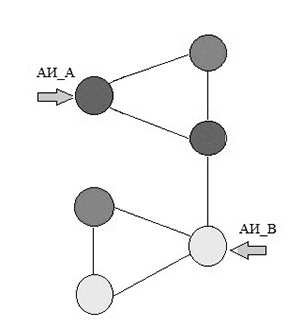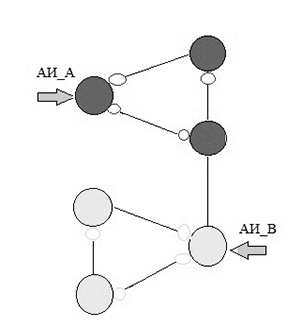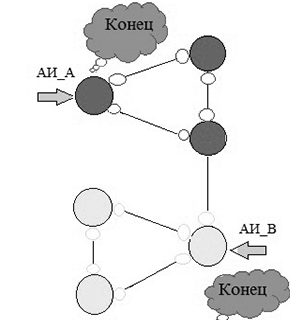
Рисунок 2 – Робота агентів дослідників
(анімація: обсяг - 126 КБ, кількість кадрів - 11, розмір - 320х325)
Пропонована стратегія має ряд відмінних властивостей:
1) розпізнаваний граф G не відомий агентам.
2) агенти на кожному кроці можуть володіти інформацією тільки про мітки елементів з околиці Q (v) поточної вершини v
3) при відвідуванні вершин графа G агенти створюють неявну нумерацію пройдених вершин: при першому відвідуванні вершини вона забарвлюється агентом А в червоний колір (агентом B в жовтий колір) і їй фактично ставиться у відповідність номер, рівний значенню змінної Сч_А (Сч_B в разі агента B ).
Відзначимо, що змінні Cч_А і Сч_В приймають відповідно непарні і парні значення. На основі цієї нумерації і відбувається відновлення графа G, шляхом побудови изоморфного йому графа H. У процесі обходу агенти будують неявні дерева обходу в глибину і щодо цих дерев всі ребра поділяються на три види: деревні – ребра, що належать деревах і забарвлювані при першому проходженні по ним в червоний (жовтий) колір; зворотні - ребра, що з'єднують вершини одного дерева, але не належать самому дереву і забарвлювані при першому проходженні в чорний колір; перешийки - ребра, які з'єднують дерева обходу різних агентів. Деревні ребра проходяться принаймні 2 рази і при останньому проході фарбуються агентами в чорний колір. Зворотні проходяться кожним агентом по два рази: перший, що пройшов по ньому, агент мітить перешийок, фарбуючи його в червоний (агент А) або в жовтий (агент В) колір, другий, минулий по ньому, агент розпізнає перешийок і фарбує його в чорний колір.
Червоні (жовті) вершини графа G, на кожному кроці алгоритму, утворюють червоний (жовтий) якщо це не повернення для розпізнання перешейков) – коротшає, при розпізнаванні зворотного ребра і перешейков - не змінюється. Вершина, у якої все інцідентние ребра розпізнані, забарвлюється в чорний колір. Алгоритм закінчує роботу, коли червоний і жовтий шляху стають порожніми, а всі вершини чорними.
Запропоновано базовий метод відновлення раніше невідомого графа з точністю до міток на елементах графів, за допомогою пересувається по ньому агента.
Базовий метод допускає модифікації, які дозволяють отримати кращу оцінку часової складності і спрощують агента, який пересувається по графу, проте, накладають додаткові обмеження на відновлюваний граф.
5.3 Модифікації базового алгоритму розпізнавання
Перша модифікація базового алгоритму розпізнавання. Перша модифікація базового алгоритму полягає в наступному: агенти - дослідники поміщаються в різні вершини графа G, ці вершини відразу забарвлюються в червоний і жовтий кольори для агентів A і B відповідно. Агенти-дослідники пересуваються одночасно, покроково передаючи агенту-експериментатору інформацію, агент-експериментатор, в свою чергу, обробляє отримані від них дані на основі яких і будує граф H ізоморфний графу G з точністю до відміток на графі [7].
Друга модифікація базового алгоритму розпізнавання. Друга модифікація базового алгоритму спрямована на оптимізацію процедур розпізнавання зворотних ребер і перешейков, а також роботи агентів. Що, зрештою, дозволило на порядок знизити верхню оцінку тимчасової, комунікаційної складнощів алгоритму і числа переходів по ребрах, що здійснюються агентами-дослідниками, а також дозволило позбутися залежності пам'яті агентів-дослідників від числа вершин розпізнаваного графа. Це дало можливість використовувати одних і тих же агентів для розпізнавання будь-якого графа з розглянутого безлічі [7].
Третя модифікація базового алгоритму розпізнавання. У попередніх модифікаціях агенти-дослідники взаємодіють між собою виключно за рахунок забарвлення елементів графа, що дозволяє значно знизити комунікаційну складність алгоритму. У третій модифікації базового алгоритму розпізнавання агентам-дослідникам додана можливість вписувати номери безпосередньо в вершину, а також збільшена, в порівнянні з попередніми модифікаціями, пам'ять агентів-дослідників. Це дало можливість знизити тимчасову складність виконання алгоритму з O(n³) до O(n²), числа переходів по ребрах, що здійснюються агентами-дослідниками з O(n³) до O(n), а комунікаційної складності з O(n³) до O(n²×log (n²)). Ємнісна складність при цьому залишилася незмінною [7].
5.4 Детермінована розмітка вершин графа
Завдання розмітки вершин кінцевого простого зв'язкового неорграфа здійснюється за допомогою блукаючого по ньому агента. Розмітка проводиться за один прохід так, що в околиці кожної вершини всі вершини розмічені різними мітками.
Завдання побудови Д-розмітки формулюється таким чином. Агент встановлюється в довільну вершину апріорі невідомого йому графа, всі вершини якого позначені однією і тією ж міткою. Агент повинен здійснити Д-розмітку вершин цього графа, причому якщо вершина вже позначена агентом, то її мітка надалі не змінюється.
Побудова мінімальної Д-розмітки на основі тільки локальної інформації про вершини графа представляється в загальному випадку неможливим. Тому в роботі розглядається побудова «жадібних» алгоритмів розмітки. Показано, що за допомогою Д-розмітки агент може відновити досліджуваний граф з точністю до ізоморфізму і що мінімальна Д-розмітка відновленого графа може бути отримана застосуванням до його транзитивне замикання відомих в теорії графів алгоритмів правильної розмальовки.
Метод Д-розмітки вершин агентом A3 заснований на обході графа завширшки. При цьому для неявного іменування вершин використовуються мітки шляхів в них з початкової вершини по дереву обходу. Розроблено відповідний поліноміальний алгоритм.
Збільшення розміру спостережуваної агентом околиці (т. Е. Обсягу його вхідної інформації) призводить до збільшення складності робота, який реалізує функції агента, тому доцільно розглянути модель з обмеженнями на розмір [5].
Висновки
Проведено огляд і аналіз існуючих алгоритмів по розпізнаванню графа колективом агентів. В результаті були виявлені основні переваги і недоліки аналізованих алгоритмів. Вивчено основні визначення і поняття.
Велика роль в аналізі існуючих алгоритмів була відведена базовому алгоритму. У даному алгоритмі кожен агент-дослідник використовує дві різні фарби. У цьому алгоритмі вперше, поряд з тимчасовою T(n), ємнісний S(n) складнощами і числом переходів по ребрах, що здійснюються агентами дослідниками, досліджуєсться комунікаційна складність К(n) – складність, обумовлена кількістю повідомлень, якими потрібно обмінятися агентам-дослідникам з агентом екпериментатором для розпізнавання графа.
Розглянуті також модифікації базового алгоритму, що утворюють спектр алгоритмів розпізнавання, заснованих на методі обходу графа в глибину, з розпізнаванням зворотних ребер і ребер перешейков.
Список джерел
- Стёпкин А.В. Использование коллектива агентов для распознавания графа// Компьютерные исследования и моделирования. – 2013. – №4. – С. 525-532.
- Стёпкин А.В.Распознавание конечных неориентированных графов коллективом агентов // Журнал обчислювальної та прикладної математики. – 2013. – №2(112). – С. 161-168.
- Грунский И.С., Татаринов Е.А. Распознавание конечного графа блуждающим по нему агентом // Прикладная дискретная математика. Приложение. Комбинаторный анализ. Теория графов. – 2009.– №1. – С. 492-496.
- Стёпкин А.В. Возможность и сложность распознавания графов тремя агентами // Таврический вестник информатики и математики. – 2012. – №1 (20). – C. 88–98.
- Грунский И.С., Сапунов С.В. Детерминированная разметка вершин графа блуждающим по нему агентом // Прикладная дискретная математика. Приложение. – 2012. – №5. – C. 89–91.
- Килибарда Г., Кудрявцев В. Б., Ушчумлич Щ. Независимые системы автоматов в лабиринтах // Дискретная математика. – 2003. – Т. 15, вып. 2. – С. 3–39.
- Стёпкин А.В. Распознавание графов с помощью коллектива агентов // Диссертация на соискание ученой степени кандидата физико-математических наук. – 2015. – С.1-185.
- Стёпкин А.В. Распознавание конечных графов тремя агентами // Искусственный интеллект. – 2011. – №2. – С. 84-93.
- Материал из свободной электронной библиотеки Википедия: словарь теории графов. Электронный ресурс. Режим доступа: http://ru.wikipedia.org/wiki/Глоссарий_теории_графов
- Кудрявцев В.Б., Алешин С.В., Подколзин А.С. Введение в теорию автоматов. – М.: Наука, 1985. – 320 с.
- Оре О. Теорія графів / Оре О. – М. : Наука, 1980. – 340 с.
Важливе зауваження
При написанні даного автореферату магістерська робота ще не завершена. Можлива дата завершення – 1 грудня 2015. Повний текст роботи, а також матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.
