Abstract
Content
- Introduction
- 1. The effect of the ionosphere on the parameters of observations
- 2. The effect of the ionosphere on the parameters of observations
- 3. Mathematical models of atmospheric delays
- 3.1 Mathematical models to account for ionospheric delay
- 3.2 Mathematical models to account for tropospheric delay
- Conclusions
- References
Introduction
The speed of propagation is of particular importance for any distance-measuring system. That rate, multiplied by the measured the time interval distribution, provides a measure of distance. Signals transmitted by satellite GPS / ГЛОНАСС, on their way to a receiver located on or near the surface of the Earth, we are forced to pass through the Earth's atmosphere. The interaction of the signals from the constituent charged particles and neutral atoms and molecules in the atmosphere, their speed and direction of the change. The most characteristic is the dissemination of the troposphere, the tropopause, stratosphere and ionosphere.
The ionosphere spans the atmosphere between 70 and 1500 km above the Earth's surface and is characterized by the presence of free (negatively charged) electrons. The carrier frequencies below 30 MHz, reflected from the ionosphere, it penetrates only the higher frequencies. The ionosphere is a dispersive medium, that is the modulation carrier frequency and carrier phase are subjected to different influences, and this effect is a function of the carrier frequency [ 2 ].
The combined impact of the neutral atmosphere consisting of the troposphere, the stratosphere is called the tropopause and tropospheric refraction. Action tropospheric refraction occurs to heights of about 40 km from the Earth's surface. For frequencies below 30 GHz troposphere behaves as a non-dispersive (nonscattering) medium, ie the refraction does not depend on the frequency of the signal transmitted through it.
Aims and objectives:
The purpose of research – development techniques into account the effect of the ionospheric and tropospheric delays on the measurement results of satellite navigation systems.
To identify the most effective type of shooting must perform the following practical tasks:
objectives:
1.Realize mathematical model to determine the ionospheric delay.
2.Realize mathematical model to determine the tropospheric delay.
3.Create software for amendment of the ionosphere and the troposphere in the measurement results.
The object of study – the impact of the various layers of the atmosphere to the results of satellite measurements.
The subject of the study – to increase the accuracy of determining the coordinates through post-processing of satellite navigation measurements.
Relevance of the topic is increasingly widespread use of satellite radio navigation satellite systems. The signal on its path from the satellite to the receiver passes through the various layers of the atmosphere where influenced. If carefully consider this effect, it is possible to achieve a high accuracy.
1. The effect of the ionosphere on the parameters of observations
The ionosphere, which extends from an altitude of about 70 km to 1000 km above the Earth, is a region of ionized gases (free electrons and ions). Ionization is caused by solar radiation, and the state of the ionosphere is mainly determined by the intensity of solar activity. The ionosphere is composed of layers (called layers D, E, F1 and F2) at different heights, each with its rate of formation and the loss of free electrons. The peak electron density (number of electrons per cubic meter) are in the range of heights of 250-400 km (layer F2) [ 3 ].
The physical characteristics of the ionosphere change from day to night in a wide range. When the sun rises, its ultraviolet radiation begins to decompose gas molecules (mainly H2 and He at high altitudes and at lower altitudes – O2 and N2) ions and free electrons. The peak electron density occurs about 2 hours after local noon, and then begins to decrease density. At night, the ionization occurs, and the ions and electrons are recombined with each other and reducing the number of free electrons. There are significant changes in the seasons and phases of the solar activity. It may also show significant variability from day to day, depending on solar activity and geomagnetic disturbances. There are also unpredictable and short-term impact of local anomalies (moving ionospheric disturbances).
The speed of propagation of radio signals in the ionosphere depends on the number of free electrons in their path, determined by the total electron density TEC (Total Electron Content) [ 4 ]. This is the number of electrons contained in the column cross-section of 1 m2, extending from the receiver to the satellite:

where ne(s) - variable electron density along the signal path, and the integration is performed along the signal path from the satellite to the receiver R. S The path length through the ionosphere, the shortest in the direction of the zenith, and therefore has the lowest TEC value in a vertical direction (TECV). The value is measured in units TEC TECU (TEC Units), defined as the 1016 of electrons / m 2. Typically TECV varies between 1 and 150 TECU. In this place and at this time TECV may vary by 20-25% from its monthly average. Current models of the ionosphere do not provide an adequate representation of changes in the TEC between the day and night.
The ionosphere is usually calm demeanor in temperate latitudes, but can fluctuate near the equator and the magnetic poles. The area with the highest ionospheric delay is within ± 20° of the magnetic equator. Solar flares and magnetic storms follow can create extensive and rapid fluctuations in the carrier phase (called scintillations) in the amplitude (called damping) SRNS. This phenomenon, albeit brief and infrequent in mid-latitudes, could create difficulties in the continuous monitoring of signals in the polar and equatorial regions.
2. The effect of the troposphere on the parameters of observations
The neutral atmosphere (troposphere, the tropopause and stratosphere) is a non-dispersive medium. Its effect is referred to as tropospheric refraction that does not depend on the frequency and, therefore, affects the code modulation, and the phase of the carrier in the same manner. Effect represents the delay (with the same sign, that codes for the ionosphere) which reaches 2.0-2.5 m in the direction of the zenith and increases approximately proportionally cosecant elevation angle, reaching a height of 20-28 m at 5 °. Ranging are longer than the geometric distance between the receiver and the satellite. The delay depends on the temperature, humidity and pressure, It varies with the height of the user and the type of terrain under the signal path. Due to the fact that the tropospheric refraction does not depend on the frequency of the carrier, it is impossible to eliminate a dual frequency observation, as opposed to ionospheric refraction.
The refractive index N is conveniently determined by the index of the refractive index n as the N = (n-1) • 10-6. In analogy with the expressions for ionospheric refraction tropospheric delay can be represented as

The refractive index of air of electromagnetic waves used in satellite positioning systems, depending on the state of the atmosphere, i.e. the air temperature T, pressure P, and the humidity (water vapor pressure) e:

The refractive index is a function of the position of points in space through which the signal path, as the meteorological field, the atmosphere is considered to be regular only conditionally. It is not uniform, particularly near the surface. Therefore, to calculate the path traveled by the signal from the satellite and found a direct or indirect definitions, you must know the actual refractive index of air along the way.
The actual average refractive index n is theoretically determined by the expression

This equation assumes that a function of N(x) from the path of x is known. It can only be determined when reliable assumptions about the structure of the atmosphere, or from direct measurements [ 1 ].
3. Mathematical models of atmospheric delays
The atmosphere changes the velocity (magnitude and direction) radio propagation. This phenomenon is called refraction. The change in propagation speed of the signal change time, which is the basis of measurements in the GPS. Let us briefly consider options for the mathematical definition of delays for different layers of the atmosphere.

Figure 2 – The refraction of the GPS signals in the Earth's atmosphere leads to changes in the speed and direction of the signal.
(Animation: 5 frames, 15 cycles of repetition, 101 kilobytes)
3.1 Models of ionospheric delay
point model of the ionosphere. To simplify geometric modeling the ionosphere can be regarded as a thin shell surrounding the Earth (Figure 3). The length of the signal path is varied by changing the position of the satellite in the sky, the lower the satellite, the longer path and longer TEC. Assuming that the lateral gradients of electrons are missing, you can take a simple and compact feature for TEC along the signal path through the vertical TEC (TECV) and multiply it by the amount of elongation of the signal path. This factor is called the tilting factor OF (also used the term ionospheric mapping function). To represent the position of the satellite relative to the receiver R S we introduce the zenith distance.

Figure 3 – Passage through the ionosphere radio beam
The average height of the ionospheric layer, or an average ionospheric height h I is usually taken in the range of 300-400 km. Ionospheric point IP is defined as the point of intersection of the line of sight with a spherical layer at a height hI [ 5 ]. Its projection along the radius vector to the earth's surface is called podionosfernoy point. Now you can link to the TEC TECV zenith distance on the path lengths through a thin layer of the ionosphere as a

Because of the triangle formed by the Earth's center, the receiver R and ionospheric point IP of the law of sines, we have:

where RE - the average radius of the Earth, equal to 6371 km. This yields an ionospheric tilt factor for OFI zenith distance

The magnitude OFI is in the range from one (for the direction of the zenith) to about three to elevation angle is 5°.
The relation (5) can be directly transferred to the group delay or phase advance for the SRNS. Designating ionospheric delay as a function of the zenith distance I, we have:

zenith ionospheric delay IZ, ie waypoint delay in the zenith direction generally varies in the middle latitudes of about 1-3 m night to 5-15 m in the afternoon. At the peak of the solar cycle of activity was observed at the equator zenith delay of 36 m. Consequently, the value of I and IZ must relate to one and the same time, namely the moment of observation t.
Evaluation of delay dual-frequency measurements. A user with dual frequency equipment (with L1-L2), may estimate the ionospheric group delay and phase advance on Measurements and substantially eliminate the influence of the ionosphere as a source of measurement error. The equation for the pseudo-range measurements by introducing an additional subscript for measurements on L1 and L2.
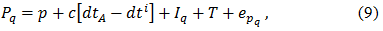
where q = L1 or L2. Joining members of non-ionospheric effects and modeling of the ionospheric delay, which depends on the square of the frequency, we can write the above equation as the

where PL1 and PL2 – pseudorange measurements, respectively L1 or L2, fL1 and fL2 – respective carrier frequencies, and P* – pseudofree from the influence of the ionosphere, in the absence of the pseudo-measurement of ionospheric effects, and the value of A = 40.3TEC it is an unknown parameter. Because dual-frequency measurements can be determined P* and A. For example, ionospheric group delay is equal to L1
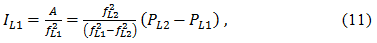
and pseudofree from the influence of the ionosphere
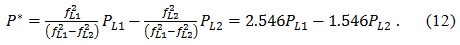
There are two comments on the ionosphere-free pseudoranges (12). Firstly, in these measurements as in P L1, and a P L2 fully present errors due to satellite clock, ephemeris and troposphere. Second, with the exception of the ionospheric influence is necessary to pay: ionospheric-free pseudo significantly more noisy than the pseudo measured on L1 and L2. If we simulate multipath and receiver noise at L1 and L2 uncorrelated and have the same variance noise ionosphere-free pseudo approximately sqrt (2.5462 +1.5462) = 3 More than the noise in the L1 or L2. In fact, the assumption of no correlation is justified, but the noise in the measurements on L2 than in modern receivers for SPS [ 1 ].
Carrier phase measurements are much less noisy, and you can try to estimate the ionospheric phase lead based on them. We write the expression for carrier phase measurements, introducing notation to distinguish measurements on the L1 or L2.
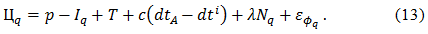
The equations similar to (11) or (12) can be written to ionospheric-free carrier phase with the inclusion of as many as ambiguities. Thus, the phase advance equal to L1
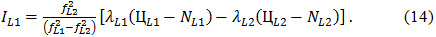
Evaluation of ionospheric delay measurements code contains no ambiguity, but rather coarse. The corresponding estimate for the phase measurement is accurate. Since the observation phase underway for a long time and maintaining constant NL1 and NL2, you can use (14) for estimating changes in ionospheric delay between the ages of measurements in real time. This change is called a differential delay, and Rating (14) has a centimeter-level accuracy. Noisy estimate ionospheric delay on the codes can be smoothed estimated differential delay of the phase measurement.

Figure 4 – Changing the ionospheric delay for one day
3.2 Models of tropospheric delay
Model refractive index and tropospheric delay Hopfield. Hopfield model (Helen S. Hopfield) based on the ratio between the refractive indices at the height h and the earth's surface. These relationships were derived empirically by measuring a large volume. The resulting model is called model with the profile of the refractive index of the fourth order:
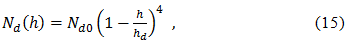
where h – height of the antenna, Nd0 – dry refractive index on the surface, hd – (= 43 km) defines the height of the antenna, which measure the refractive index is zero Nd (hd) = 0 [ 6 ].
Hopfield model for wet refractive index similar to (15):
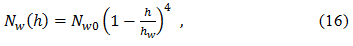
where Nw0 – wet index of refraction at the surface, and hw = 12 km.
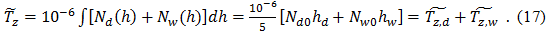
The expressions for dry and wet refractive index:

The values of Tz, d up 2.3-2.6 m at sea level and become smaller with increasing height: about 2 m at a height of about 1.5 km and about 1 meter on the tops of the peaks in the Himalayas. Appropriate wet delay depends on the distribution of water vapor along the signal path and can be very variable. Models wet delay Tz, d, based on meteorological data for the Earth's surface is usually less accurate, their typical error of 1-2 cm. Using the average meteorological conditions, and not the actual measurements, introduces additional modeling errors in the dry and in the wet delay and error in the full zenith delay may be 5-10 cm.
To change the direction of the zenith to the height E of the Hopfield introduced dry and wet mapping functions:
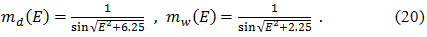
As a result, the total tropospheric delay for height E is obtained by the formula:
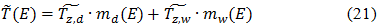
Hopfield has developed several models of the tropospheric delay are different ways of integration profiles.
Also, there is another accounting model the tropospheric delay – Saastamoinen model [ 7 ]. It was developed using the gas laws and simplifying assumptions relating to changes in pressure, temperature and humidity high. Dry and wet zenith delays are given as

where T0 – the temperature (in Kelvin), P0 – full pressure and e0 – the partial pressure of water vapor (both millibars), all defined in the location of the antenna measurements or modeling data standard atmosphere, f – latitude, and H is the height of the antenna above sea level (km).
Conclusion
In the course of performance have been researched and implemented a mathematical model defining the ionospheric and tropospheric delays.
After the software implementation will be carried out the experimental part. It will be the comparison of the results created by me and specialized software. In the case of neglect differences between the coordinates can be implemented my program for post-processing.
This essay was written before the final completion of the work. In this regard, the final results of the research will be available in December 2015.
References
- Антонович К. М.; Использование СРНС в геодезии. Том 1 / Антонович К. М., – Москва: ФГУП
Картгеоцентр
, 2005 г. - Генике А. А., Побединский Г. Г.; Глобальные спутниковые системы определения местоположения и их применение в геодезии; Москва: ФГУП
Картгеоцентр
, 2004 г. - Большая советская энциклопедия: Ионосфера [Электронный ресурс] – http://www.worklib.ru/dic/Ионосфера/
- Студопедия: Учет влияния ионосферы [Электронный ресурс] – http://studopedia.ru/4_165018_uchet-vliyaniya-ionosferi.html/
- Фам Хоанг Лонг; Разработка методики учета влияния ионосферы при GPS – измерениях на территории Веьтнама; Диссертация на соискание научной степени к. т. н. , на правах рукописи ; Москва 2014 г.
- Клюшин Е. Б., Куприянов А. О., Шлапак В. В.;Спутниковые методы измерений в геодезии. (Часть 1).Учебное пособие. М.: Изд. МИИГАиК. УПП «Репрография», 2006 г.
- Хенриксен С., Манчини А., Човица Б.; Использование исскуственных спутников для геодезии; Москва: Издательство
МИР
, 1975 г.
