Реферат по теме выпускной работы
Содержание
- Введение
- 1. Влияние ионосферы на параметры наблюдений
- 2. Влияние тропосферы на параметры наблюдений
- 3. Математические модели атмосферных задержек
- 3.1 Математические модели для учета ионосферной задержки
- 3.2 Математические модели для учета тропосферной задержки
- Выводы
- Список источников
Введение
Скорость распространения сигналов представляет особую важность для любой дальномерной системы. Именно скорость, умноженная на измеренный интервал времени распространения, обеспечивает меру дальности. Сигналы, передаваемые спутниками GPS/ГЛОНАСС, на их пути к приемнику, расположенному на Земле или около поверхности, вынуждены проходить через земную атмосферу. В результате взаимодействия сигналов с составными заряженными частицами и нейтральными атомами и молекулами атмосферы, их скорость и направление распространения изменяются. Наиболее характерными областями распространения является тропосфера, тропопауза, стратосфера и ионосфера.
Ионосфера охватывает область атмосферы между 70 и 1500 км над поверхностью Земли и характеризуется присутствием свободных (отрицательно заряженных) электронов. Несущие частоты ниже 30 МГц отражаются от ионосферы, в нее проникают только более высокие частоты. Ионосфера является диспергирующей средой, то есть модуляции на несущей частоте и фазы несущей частоты подвергаются различному влиянию, и это влияние является функцией несущей частоты [2].
Объединенное влияние нейтральной атмосферы, состоящей из тропосферы, тропопаузы и стратосферы называется тропосферной рефракцией. Действие тропосферной рефракции происходит до высот примерно 40 км от поверхности Земли. Для частот ниже 30 ГГц тропосфера ведет себя как недиспергирующая (нерассеивающая) среда, то есть рефракция не зависит от частоты сигнала, передаваемого через нее.
Цели и задачи:
Цель исследования – разработка методики учета влияния ионосферной и тропосферной задержки на результаты измерений спутниковых радионавигационных систем.
Задачи:
1.Разработать математическую модель для определения ионосферной задержки.
2.Разработать математическую модель для определения тропосферной задержки.
3.Создать программное обеспечение для внесения поправок по ионосфере и тропосфере в результаты измерений.
Объект исследования – влияние различных слоев атмосферы на результаты спутниковых измерений.
Предмет исследования – повышение точности определения координат при постобработке спутниковых радионавигационных измерений.
Актуальность темы заключается во все более широком применении спутниковых радионавигационных спутниковых систем. Сигнал на своем пути от спутника к приемнику проходит через различные слои атмосферы, где подвергается влиянию. Если тщательно учитывать это влияние, то можно достичь более высокой точности измерений.
1. Влияние ионосферы на параметры наблюдений
Ионосфера, простирающаяся от высоты около 70 км до примерно 1000 км над Землей, является областью ионизованных газов (свободных электронов и ионов). Ионизация вызывается солнечной радиацией, и состояние ионосферы определяется преимущественно интенсивностью солнечной активности. Ионосфера состоит из слоев (называемых слоями D, E, F1 и F2) на различных высотах, каждый со своими скоростями образования и потери свободных электронов. Пик электронной плотности (количество электронов в кубическом метре) приходится на диапазон высот в 250-400 км (слой F2) [3].
Физические характеристики ионосферы изменяются ото дня к ночи в широких пределах. Когда Солнце восходит, его ультрафиолетовое излучение начинает разлагать молекулы газа (в основном H2 и He на больших высотах, а на меньших высотах – O2 и N2) на ионы и свободные электроны. Пик электронной плотности наступает около 2 часов после местного полдня, а затем плотность начинает уменьшаться. Ночью ионизация не происходит, и ионы и электроны находят друг друга и рекомбинируют, уменьшая количество свободных электронов. Наблюдаются значительные изменения в зависимости от времени года и фазы солнечной активности. Может также проявляться значительная изменяемость ото дня ко дню, в зависимости от солнечной активности и геомагнитных нарушений. Есть также непредсказуемые краткосрочные влияния и локальные аномалии (подвижные ионосферные нарушения).
Скорость распространения радиосигналов в ионосфере зависит от числа свободных электронов на их пути, определяемых величиной полной электронной концентрации TEC (Total Electron Content) [4]. Это число электронов, содержащихся в столбе сечением в 1 м2, простирающемся от приемника до спутника:

где ne(s) - переменная электронная плотность вдоль пути сигнала, а интегрирование производится вдоль пути сигнала от спутника S к приемнику R. Длина пути через ионосферу самая короткая в направлении зенита, и поэтому TEC имеет наименьшее значение в вертикальном направлении (TECV). Величина TEC измеряется в единицах TECU (TEC Units), определяемых как 1016 электронов/м2. Обычно TECV изменяется между 1 и 150 TECU. В данном месте и в данное время TECV может изменяться на 20-25% от его среднемесячного значения. Современные модели ионосферы не обеспечивают адекватное представление изменений в TEC между сутками.
Ионосфера обычно имеет спокойное поведение в умеренных широтах, но может флуктуировать вблизи экватора и магнитных полюсов. Район с наивысшей ионосферной задержкой лежит в пределах ±20° от магнитного экватора. Солнечные вспышки и последующие магнитные бури могут создавать обширные и быстрые флуктуации в фазе несущей (называемые сцинтилляциями) и в амплитуде (называемые затуханиями) сигналов СРНС. Это явление, хотя и кратковременное и нечастое в средних широтах, может создавать трудности в непрерывном отслеживании сигналов в полярных и экваториальных районах.
2. Влияние тропосферы на параметры наблюдений
Нейтральная атмосфера (тропосфера, тропопауза и стратосфера) является недиспергирующей средой. О ее влиянии говорят как о тропосферной рефракции, которая не зависит от частоты и, следовательно, влияет и на кодовую модуляцию, и на фазу несущей одинаковым образом. Влияние представляет задержку (с тем же знаком, что у ионосферы для кодов), которая достигает 2.0-2.5 м в зенитном направлении и увеличивается примерно пропорционально косекансу угла высоты, достигая 20-28 м на высоте 5°. Измеренные дальности оказываются длинней, чем геометрическое расстояние между приемником и спутником. Задержка зависит от температуры, влажности и давления, изменяется с высотой пользователя и с типом местности под траекторией сигнала. Из-за того, что тропосферная рефракция не зависит от частоты несущей, ее невозможно устранять в двухчастотных наблюдениях, в отличие от ионосферной рефракции.
Показатель преломления N удобно определять через индекс показателя преломления n как N=(n-1)•10-6. По аналогии с выражениями для ионосферной рефракции тропосферную задержку можно представить как

Показатель преломления воздуха для электромагнитных волн, используемых в спутниковых системах определения местоположения, зависит от состояния атмосферы, то есть от температуры воздуха T, давления P, и влажности (давления водяных паров) e:

Показатель преломления является функцией положения точек пространства, через которые проходит путь сигнала, так как метеорологическое поле атмосферы считается регулярным лишь условно. Оно является неоднородным, особенно вблизи поверхности земли. Поэтому, для вычисления пути, пройденного сигналом спутника и найденного из прямых или косвенных определений, необходимо знать действительный показатель преломления воздуха вдоль пути.
Действительный средний показатель преломления n теоретически определяется выражением

Это равенство предполагает, что функция N(x) от пути x известна. Она может быть определена только при достоверных предположениях о строении атмосферы или из непосредственных измерений [1].
3. Математические модели атмосферных задержек
Атмосфера изменяет скорость (величину и направление) распространения радиосигналов. Это явление называется рефракцией. Изменение в скорости распространения изменяет время прохождения сигнала, которое является основой измерений в GPS. Рассмотрим кратко варианты математического определения задержек для различных слоев атмосферы.

Рисунок 2 – Рефракция сигналов GPS в атмосфере Земли приводит к изменениям в скорости и в направлении сигнала.
(анимация: 5 кадров, 15 циклов повторения, 101 килобайт)
3.1 Модели ионосферной задержки
Точечная модель ионосферы. Для упрощения геометрического моделирования ионосферу можно рассматривать как тонкую оболочку, окружающую Землю (рисунок 3). Длина пути сигнала варьируется при изменении положения спутника на небе, чем ниже спутник, тем длиннее путь и больше TEC. Считая, что боковые градиенты электронов отсутствуют, можно принять простую и компактную характеристику для TEC вдоль пути сигнала через вертикальную TEC (TECV) и умножить ее на величину удлинения пути сигнала. Этот множитель называется фактором наклона OF (используется также термин ионосферная функция отображения). Чтобы представить положение спутника S относительно приемника R введем в рассмотрение зенитное расстояние.

Рисунок 3 – Прохождение радиолуча через ионосферу
Средняя высота ионосферного слоя, или средняя ионосферная высота hI обычно берется в диапазоне 300-400 км. Ионосферная точка IP определяется как точка пересечения линии визирования со сферическим слоем на высоте hI [5]. Ее проекция по радиусу-вектору на земную поверхность называется подионосферной точкой. Теперь можно связать TECV с TEC на зенитном расстоянии через длины путей тонкого ионосферного слоя как

Из треугольника, образованного центром Земли, приемником R и ионосферной точкой IP по теореме синусов имеем:

где RE – средний радиус Земли, равный 6371 км. Отсюда получается ионосферный фактор наклона OFI для зенитного расстояния

Величина OFI лежит в диапазоне от единицы (для направления в зенит) до примерно трех для угла высоты в 5°.
Соотношение (5) можно непосредственно перевести в групповую задержку или фазовое опережение для сигналов СРНС. Обозначив ионосферную задержку как функцию зенитного расстояния I, имеем:

Ионосферная зенитная задержка IZ, то есть путевая задержка в зенитном направлении обычно изменяется в средних широтах примерно от 1-3 м ночью до 5-15 м в полдень. В пик солнечного цикла активности на экваторе наблюдалась зенитная задержка в 36 м. Следовательно, величины I и IZ должны относиться к одному и тому же моменту, а именно моменту наблюдений t.
Оценивание задержки по двухчастотным измерениям. Пользователь, имеющий двухчастотную аппаратуру (с L1-L2), может оценивать ионосферную групповую задержку и фазовое опережение по измерениям и существенно исключать влияние ионосферы как источника ошибок измерений. Запишем уравнение для измерения псевдодальности, введя дополнительный нижний индекс для измерений на L1 или L2.
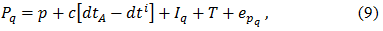
где q=L1 или L2. Объединяя члены, не связанные с ионосферным эффектом и моделированием ионосферной задержки, зависящей от квадрата частоты, можно записать приведенное выше уравнение как

где PL1 и PL2 – измеренные псевдодальности соответственно на L1 или L2, fL1 и fL2 – соответствующие частоты несущих, а P* - псевдодальность, свободная от влияния ионосферы, то есть измерение псевдодальности при отсутствии ионосферного эффекта, и величина A=40.3TEC является неизвестным параметром. Из двухчастотных измерений можно определить P* и А. Например, ионосферная групповая задержка на L1 равна
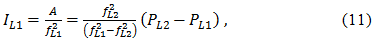
а псевдодальность, свободная от влияния ионосферы
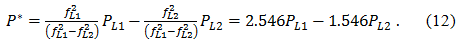
Есть два замечания по поводу ионосферно-свободной псевдодальности (12). Во-первых, в этих измерениях, как в PL1, так и в PL2 в полной мере присутствуют ошибки из-за часов спутника, эфемерид и тропосферы. Во-вторых, за исключение ионосферного влияния приходится платить: ионосферно-свободная псевдодальность значительно более шумная, чем псевдодальности, измеренные на L1 и L2. Если мы смоделируем многопутность и шум приемника на L1 и L2 некоррелированными и имеющими одинаковую дисперсию, то шум ионосферно-свободной псевдодальности примерно в sqrt(2.5462+1.5462)=3 больше, чем шум на L1 или L2. В действительности предположение об отсутствии корреляции обосновано, но шум в измерениях на L2 больше, чем в современных приемниках для SPS [1].
Измерения фазы несущей намного менее шумные, и можно попытаться оценить ионосферное опережение фазы, основываясь на них. Запишем выражение для измерения фазы несущей, вводя обозначения для различения измерений на L1 или L2.
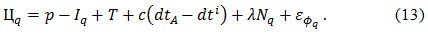
Уравнения, подобные (11) или (12) можно записать для ионосферно-свободной фазы несущей с включением целых неоднозначностей. Так, фазовое опережение на L1 равно
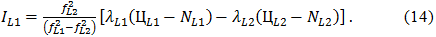
Оценка ионосферной задержки по кодовым измерениям не содержит неоднозначностей, но довольно грубая. Соответствующая оценка по фазовым измерениям оказывается точной. Поскольку наблюдения фазы ведутся продолжительное время и с сохранением постоянными NL1 и NL2, то можно использовать (14) для оценивания изменений в ионосферной задержке между эпохами измерений в реальном времени. Такое изменение называется дифференциальной задержкой, и его оценка по (14) имеет сантиметровый уровень точности. Шумные оценки ионосферной задержки по кодам можно сгладить по оценкам дифференциальной задержки из фазовых измерений.

Рисунок 4 – Изменение ионосферной задержки в течение суток
3.2 Модели тропосферной задержки
Модель показателей преломления и тропосферной задержки Хопфилд. Модель Хопфилд (Helen S. Hopfield) основана на соотношениях между показателями преломления на высоте h и у земной поверхности. Эти соотношения были выведены эмпирически по большому объему измерений. Полученную модель называют моделью с профилем показателя преломления четвертого порядка:
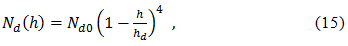
где h – высота над антенной, Nd0 – сухой показатель преломления на поверхности, а hd – (=43 км) определяет высоту над антенной, на которой показатель преломления равен нулю Nd (hd )=0 [6].
Модель Хопфилд для влажного показателя преломления подобна (15):
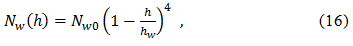
где Nw0 – влажный показатель преломления на поверхности, и hw = 12 км.
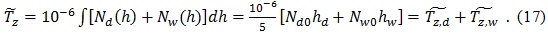
Выражения для сухого и влажного показателей преломления:

Значения Tz,d составляют 2.3-2.6 м на уровне моря и становятся меньше с увеличением высоты: около 2 м на высоте около 1.5 км и около 1 м на вершинах пиков в Гималаях. Соответствующая влажная задержка зависит от распределения паров воды вдоль пути сигнала и может быть очень переменной. Модели влажной задержки Tz,d, основанные на метеорологических данных для поверхности Земли, обычно менее точны, их типичная ошибка 1-2 см. Использование средних метеорологических условий, а не действительных измерений, вводит дополнительные ошибки моделирования и в сухую, и во влажную задержку, и ошибка в полной зенитной задержке может быть 5-10 см.
Для перехода от направления в зенит к высоте E у Хопфилд вводятся сухая и влажная функции отображения:
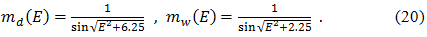
В итоге полная тропосферная задержка для высоты Е получается по формуле:
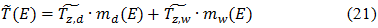
Хопфилд разработала несколько моделей тропосферной задержки, которые отличаются способами интегрирования профилей.
Также, существует и другая модель учета тропосферной задержки – модель Саастамойнена [7]. Она была разработана с использованием газовых законов и упрощающих предположений, касающихся изменений в давлении, температуре и влажности с высотой. Сухая и влажная зенитные задержки даются как

где T0 – температура (в Кельвинах), P0 – полное давление и e0 – парциальное давление паров воды (оба в миллибарах), все определенные у местоположения антенны по измерениям или по модельным данным стандартной атмосферы, ф - широта, а H –высота антенны над уровнем моря (км).
Вывод
По ходу выполнения работы были исследованы и математически реализованы модели, определяющие ионосферную и тропосферную задержки.
После программной реализации будет проведена экспериментальная часть. Она будет заключаться в сравнении результатов созданного мной программного продукта и специализированного. В случае пренебрежительного расхождения между координатами можно будет внедрить мою программу для постобработки.
Данный реферат писался до окончательного завершения работы. В связи с этим окончательные результаты исследований можно будет получить в декабре 2015 года.
Список источников
- Антонович К. М.; Использование СРНС в геодезии. Том 1 / Антонович К. М., – Москва: ФГУП
Картгеоцентр
, 2005 г. - Генике А. А., Побединский Г. Г.; Глобальные спутниковые системы определения местоположения и их применение в геодезии; Москва: ФГУП
Картгеоцентр
, 2004 г. - Большая советская энциклопедия: Ионосфера [Электронный ресурс] – http://www.worklib.ru/dic/Ионосфера/
- Студопедия: Учет влияния ионосферы [Электронный ресурс] – http://studopedia.ru/4_165018_uchet-vliyaniya-ionosferi.html/
- Фам Хоанг Лонг; Разработка методики учета влияния ионосферы при GPS – измерениях на территории Веьтнама; Диссертация на соискание научной степени к. т. н. , на правах рукописи ; Москва 2014 г.
- Клюшин Е. Б., Куприянов А. О., Шлапак В. В.;Спутниковые методы измерений в геодезии. (Часть 1).Учебное пособие. М.: Изд. МИИГАиК. УПП «Репрография», 2006 г.
- Хенриксен С., Манчини А., Човица Б.; Использование исскуственных спутников для геодезии; Москва: Издательство
МИР
, 1975 г.
