Українська   English
ДонНТУ   Портал магистров

Реферат по теме выпускной работы

Содержание

Введение

Развитие технологии и оборудование для обработки металлов давлением, а также расширение сортамента профилей, полученных при горячей пластической деформации из различных марок сталей и сплавов, требуют непрерывного совершенствования и уточнения методов проектирования технологических процессов и конструкторских расчетов. Для решения этих задач необходимо изучение механических свойств металлов и сплавов при различных температурно-скоростных условиях деформации и разработка достоверных методов их оценки в конкретных технологических процессах для обеспечения максимальной производительности оборудования и повышение качества продукции.

Напряжение течения металла является одной из основных составляющих, которое существенно влияет на точность расчетов энергосиловых параметров в процессах обработки металлов давлением (ОМД). Известно, что напряжение течения металла при горячей пластической деформации в основном зависит от степени, скорости и температуры деформации. Повышение степени деформации приводит к увеличению напряжения течения, т.е. к увеличению упрочнения металла. Напряжение течения существенно возрастает с увеличением скорости деформации металла. С повышением температуры нагрева все прочности характеристики металла снижаются.

Поэтому исследования существующих и разработка усовершенствованных методов расчета напряжения течения металла в процессах ОМД является актуальной работой.

1. Актуальность темы

Актуальной задачей является получение эмпирических формул расчета напряжения течения металла для конструкционных, инструментальных и нержавеющих марок сталей на основе имеющейся экспериментальной информации.Анализ точности разработанных формул определения напряжения течения металла.

2. Цель и задачи исследования

Целью работы является усовершенствование методов расчета напряжения течения металла, а также разработка новых эмпирических формул и их анализ.

Основные задачи исследования:

Разработка новых формул на базе экспериментальной информации, для 44 марок сталей и анализ их точности. Анализ возможности выполнения экстраполяции расчетной информации.

Объектом исследования являются методы расчета напряжения течения металла в процессах горячей пластической деформации.

    3. Совершенствование метода и разработка эмпирических формул определения напряжения течения металла для термомеханических коэффициентов и их анализ

    В технической литературе, представлены крупные экспериментальные данные о зависимости напряжения течения металла σ от степени деформации ε, скорости деформации u и температуры T, представлены в виде кривых упрочнения. В ряде случаев, в том числе и при разработке компьютерных программ возникает необходимость в разработке эмпирических формул, необходимых для расчета напряжения течения металла σ.[1]

    3.1. Разработка новых формул на базе экспериментальной информации

    Работа является продолжением исследований, результаты которые были опубликованы раннее и в частности связаны с магистерской работой Алексея Пугача.[8] В этих работах использовали известную экспериментальную информацию σи от ε, u, t. Но не были охвачены известные графические зависимости для определения σ в виде Кε=f(ε), Кu=f(u), КT=f(Т). Соответственно не существовали компьютерные программы для обработки такой графической информации. Определение величин σ в зависимости от произвольных значений ε,u,t выполняли следующим образом[2][3]. На первом этапе в окно компьютерной программы заносятся отсканированные графики (см. рис.1).

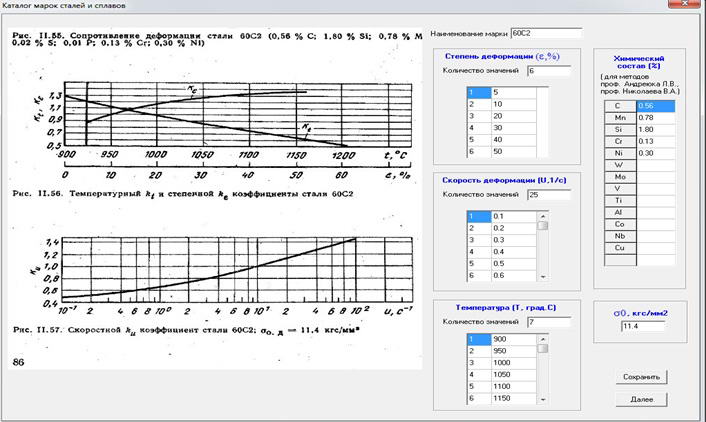
    Окно исходной информации марки

    Рисунок 1 – Окно исходной информации марки

    Затем задаются координаты узловых точек осей в натуральных значениях для ε,u,t(см. рис.2). При этом в таблицу автоматически заносятся значения координат узловых точек в единицах растрового изображения. Это позволяет установить между ними взаимно однозначное соответствие. Аналогичные действия выполняются для каждого из 3-х графиков. Когда сетки заданы, переходим к другому окну.

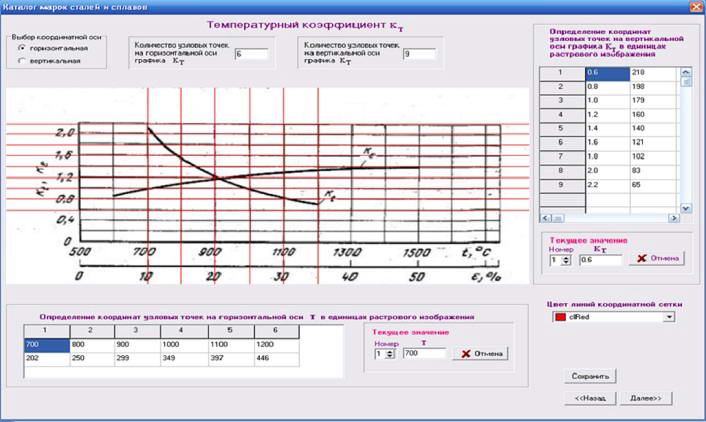
    Окно построения координатной сетки

    Рисунок 2 – Окно построения координатной сетки

    В следующем окне выполняем сплайн-интерполяцию полученной информации (см. рис.3). Нам необходимо построить сплайн кривую, соответствующую имеющейся. При этом нужно добиться полного совпадения между интерполяционной кривой и исходной. На нашем рисунке интерполяционная кривая имеет бирюзовый цвет. Если ход исходной кривой сложный, например, имеются перегибы, то сплайн - кривая может на первом этапе недостаточно точно ложится на исходную кривую. Тогда можно увеличить число точек и тем самым мы добиваемся полного совпадения между этими кривыми.

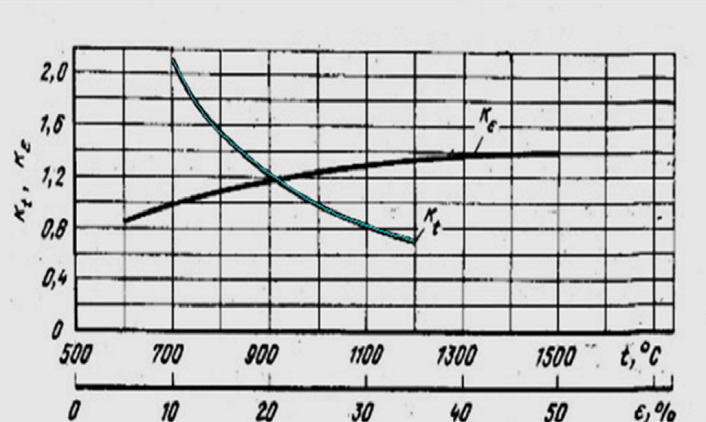
    Окно снятия экспериментальной информации и построение сплайн кривых

    Рисунок 3 – Окно снятия экспериментальной информации и построение сплайн кривых

    Рассчитанные в окне величины напряжения течения металла при заданных значениях ε,u,t автоматически передаются в таблицу, которая и обеспечивает точную аппроксимацию исходных кривых (см. рис.4). На базе этой таблицы в раннее выполненных работах создана методика расчета σ при заданных значениях ε, u, t.

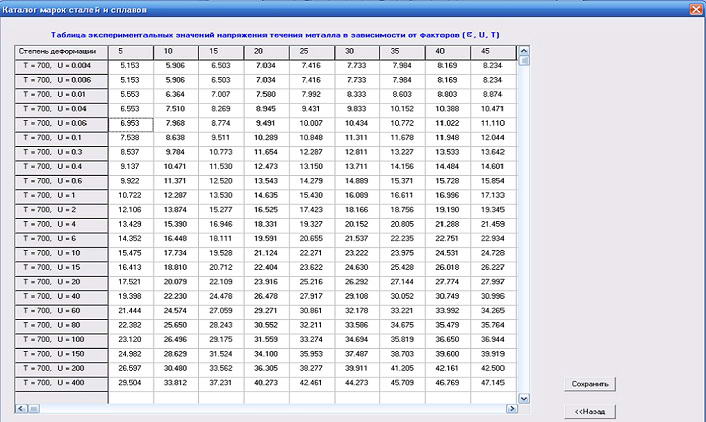
    Значение величин σ при заданных значениях факторов, полученных в ходе работы программы

    Рисунок 4 – Значение величин σ при заданных значениях факторов, полученных в ходе работы программы

    В это окно передается с предыдущего окна рассмотренная раннее таблица (см. рис.5). Также здесь указываются пределы изменения факторов, для которых будет разрабатываться формула. Затем нажимаем кнопку далее и переходим к следующему окну

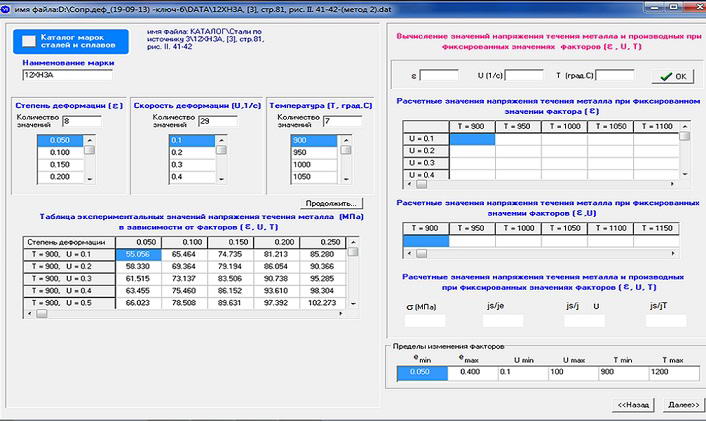
    Окно расчета σ на основе экспериментальной информации

    Рисунок 5 – Окно расчета σ на основе экспериментальной информации

    В это окно передаются пределы изменения факторов ε,u,t. Для научно- обоснованного выбора наиболее рациональных точек в области изменения факторов предложено применить метод планируемого расчетного эксперимента[5]. (см. рис.6). В этом же окне формируется план-матрица кодовых и натуральных значений факторов. В соответствии с теорией планируемого эксперимента, план-матрица для 3-х факторов всегда содержит 15 строк для определения величин σ. Планируемый эксперимент, охватывает всю заданную область изменения факторов и определяет наиболее рациональные точки для определения величин. Причем это научно-обоснованный теорией планируемого эксперимента минимум опытов. Для стали 12ХН3А здесь представлены значения напряжения течения металла σэксп, по сути полученные путем сплайн-интерполяции кривых упрочнения. На основе метода наименьших квадратов автоматически находятся константы, входящие в формулу проф. В.И. Зюзина. Затем на ее основе выполняется расчет величин σр в тех же 15-ти опытах. Найдено среднее относительное отклонение расчетных значений σр по отношению к соответствующим экспериментальным значениям. Указанное отклонение равно 1,9%. Это точность аппроксимации.

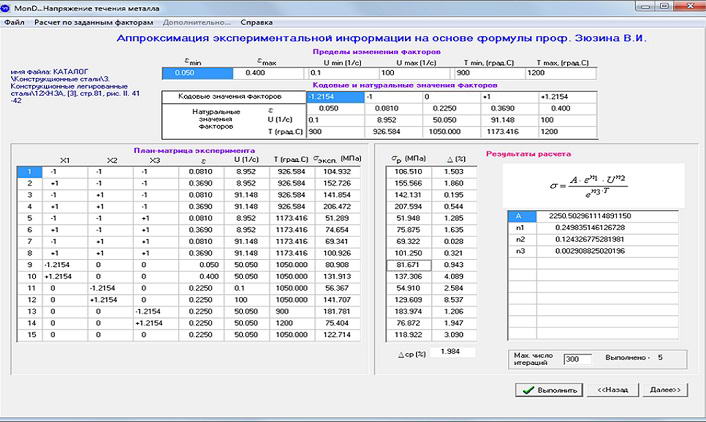
    Окно расчета констант, входящих в формулу проф. Зюзина В.И.

    Рисунок 6 – Окно расчета констант, входящих в формулу проф. Зюзина В.И.

    Аналогично было разработано окно программы, позволяющее определить константы, входящие в полином второй степени. Вид полинома представлен в правой части окна (см.рис.7). Для стали 12ХН3А представлены значения напряжения течения металла σэксп, полученные также путем сплайн-интерполяции кривых упрочнения. Найдены константы, входящие в формулу полинома второй степени, и на их основе выполнен расчет величин σр. Найдена точность аппроксимации экспериментальных значений σр.Она равна 7,1%.

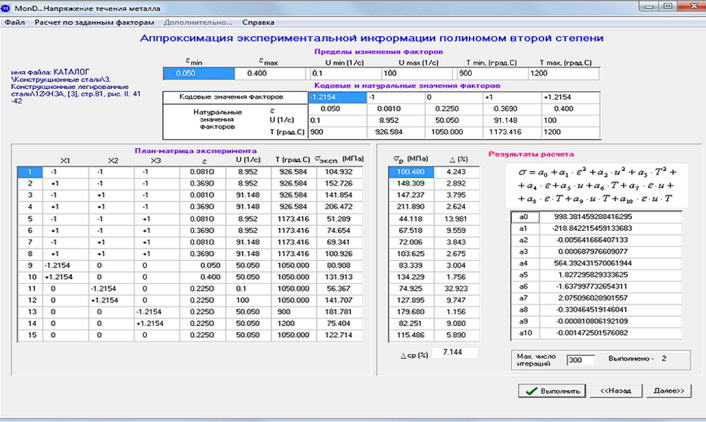
    Окно расчёта констант входящих в полином второй степени

    Рисунок 7 – Окно расчёта констант входящих в полином второй степени

    На основе представленного усовершенствованного метода выполнен расчет констант для 44 марок сталей входящих в формулу проф. Зюзина.[1] Средняя относительная ошибка аппроксимации экспериментальной информации для всех марок сталей по формуле проф. Зюзина составила 3,5%. До этой работы имелось только 6 аналогичных формул, полученных на базе экспериментальных графических, представленных зависимостей виде Кε=f(ε), Кu=f(u), КT=f(Т). Выполнен также расчет констант, входящих в представленный полином второй степени. Средняя относительная ошибка аппроксимации экспериментальной информации для всех 44-х марок сталей по этой формуле равна 4,8%.

    То есть точность на базе представленного полинома высокая, но не выше той, что дает формула, полученная проф. Зюзиным.

    3.2. Анализ точности разработанных формул напряжения течения металла для конструкционных, инструментальных и нержавеющих марок сталей

    Вопрос точности полученных формул расчета напряжения течения металла остается актуальным.Новый метод выполнения анализа точности разработанных формул, во-первых, связан с экспериментальной информации, которая не использовалась при разработке этих формул[6]. Во-вторых, была применена программа, которая в автоматизированном режиме формирует план-матрицу планируемого эксперимента для данной марки стали. С левой стороны на рисунке 8 показан планируемый эксперимент, который выполнен на базе экспериментальной информации, которая используется для проверки точности новой формулы. С правой стороны дана проверяемая формула, которую получили на базе другой экспериментальной информации[1]. Получили, что ошибка новой формулы менее 4%. Точность формул по этой методике проверили для 7-ми марок сталей.

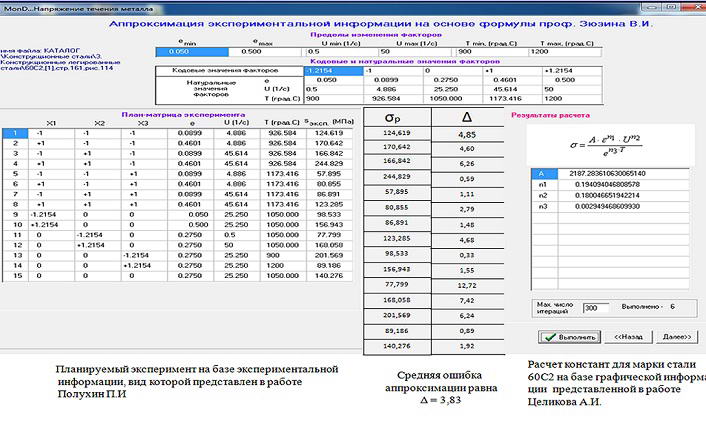
    Анализ точности разработанных формул напряжения течения металла

    Рисунок 8 – Анализ точности разработанных формул напряжения течения металла

    4. Анализ возможной экстраполяции расчетной информации в процессе определения напряжения течения металла

    Далее была поставлена новая задача о возможности выполнения экстраполяции расчетной информации на базе разработанных формул. То есть расчета напряжения течения металла по полученным формулам при значениях ε,u,t, которые лежат за теми пределами, в которых разрабатывалась формула. Весь диапазон изменения значений факторов ε,u,t разбили на две части. В интервале от 0 до 70% разрабатывали формулу. А в интервале от 80 до 100% проверяли точность формулы при экстраполяции. Это было возможно выполнить т.к. соответствующая экспериментальная информация имелась на интервале от 0 до 100% по каждому фактору(см. рис.9).

    Выполняем экстраполяцию для марки стали 4Х13

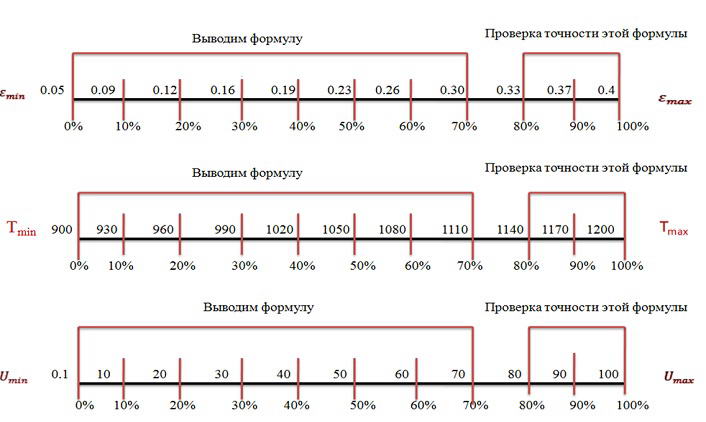
    Анализ возможной экстраполяции расчетной информации

    Рисунок 9 – Анализ возможной экстраполяции расчетной информации

    Формула разработана в диапазоне от от 0 до 70% интервала по каждому из 3-х факторов.

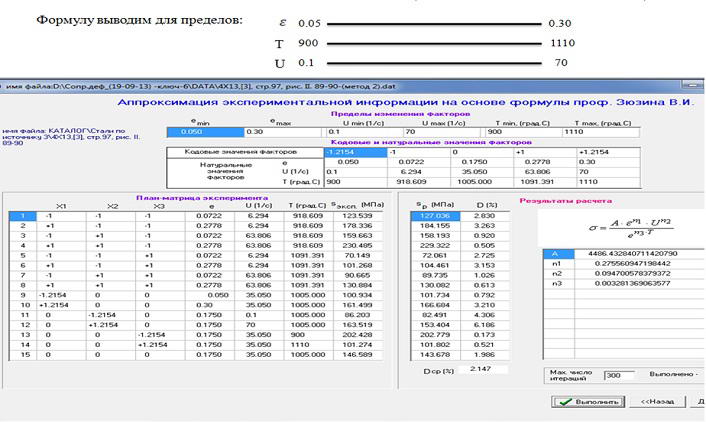
    Анализ возможной экстраполяции расчетной информации

    Рисунок 10 – Анализ возможной экстраполяции расчетной информации

    Выполнена проверка точности расчетов путем экстраполяции в диапазоне от 80 до 100% по каждому фактору. Слева на рисунке 11 представлена экспериментальная информация. Справа результаты экстраполяции. Видим, что в рассмотренном варианте ошибка не превышает 8%.

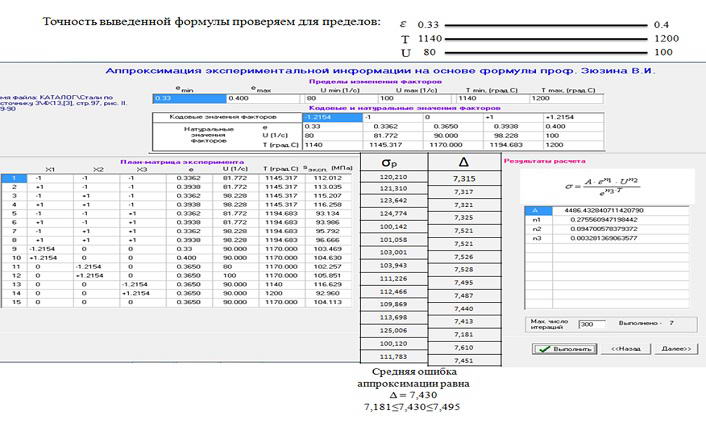
    Анализ возможной экстраполяции расчетной информации

    Рисунок 11 – Анализ возможной экстраполяции расчетной информации

    Выводы

    В работе созданы новые окна для компьютерной программы разработки формул расчета напряжения течения металла на базе сплайн интерполяции экспериментальных кривых упрочнения и планируемого эксперимента. Указанные окна использовали для получения формул на базе цифровой информации по напряжению течению металла в зависимости от степени, скорости и температуры деформации для 44 марок сталей. На основе разработанного метода определены константы для 44 конструкционных, инструментальных и нержавеющих марок сталей для двух типов формул. Определена средняя относительная ошибка аппроксимации экспериментальной информации, которая не превышает 5%.

    Выполнен анализ точности семи из полученных формул , при чем по отношению к экспериментальной информации, которая не использовалась при их разработке. Получено, что средняя погрешность расчетных данных по отношению к экспериментальным не превышает 7 %, а максимальная – 15%.

    Проведен анализ возможности экстраполяции расчетной информации для марки стали 4Х13. Средняя ошибка по отношению к экспериментальной информации составила 7,4%.

    Далее в магистерской работе планируется выполнить анализ возможной экстраполяции расчетной информации для различных марок сталей.

      Список источников

    1. Целиков А.И. Теория прокатки: Справочник / А.И. Целиков, А.Д. Томленов, В.И. Зюзин, А.В. Третьяков, Г.С. Никитин. - М.: Металлургия, 1982. - 335с.
    2. Яковченко А.В. Определение напряжения течения металла с учетом истории процесса нагружения на основе уравнения А.Надаи/ А.В.Яковчеко, Н.И.Ивлева, А.А.Пугач// Наукові праці ДонНТУ. Металургія, 2011.-Вип.12(177). - С.181 - 193.
    3. Яковченко А.В. Анализ точности известных методов расчета напряжения течения металла в зависимости от химического состава стали / А.В. Яковченко, А.А. Пугач, Н.И. Ивлева // Вісник Приазовського державного технічного університету. Сер.: Технічні науки: Зб. наук. праць. – Маріуполь: ДВНЗ «Приазов. держ. техн. ун-т», 2011. - Вип.2(23). - С. 69 - 80.
    4. Данилов А.В. Анализ и усовершенствование методов расчета напряжения течения металла в процессах горячей пластической деформации. Металлургия и обработка металлов (выпуск 12) / Материалы научно-исследовательских работ студентов и молодых ученых физико-металлургического факультета ДонНТУ. – Донецк: ДонНТУ, 2009. – С. 42,43.
    5. Винарский, М.С. Планирование эксперимента в технологических исследованиях : учеб. пособие / М.С. Винарский, М.В Лурье. – К.: Техника, 1975. – 168 с.
    6. Полухин П.И. Сопротивление пластической деформации металлов и сплавов: Справочник / П.И. Полухин, Г.Я. Гун, А.М. Галкин. – М.: Металлургия, 1983. - 352с.
    7. Примение теории ползучести при обработке металлов давлением. Поздеев А.А., Тарновский В.И., Еремеев В.И., Баакашвили В.С. Изд-во «Металлургия», 1973, 192с.
    8. Пугач А.А.Совершенствование метода получения расчетных эмпирических формул для расчета напряжения течения металла.Металлургия и обработка металлов/ Материалы Всеукраинской научно-практической конференции студентов. - Донецк: ДонНТУ, 2012. - 209 с. - С. 56 - 57.