Русский   English
ДонНТУ   Портал магістрів

Реферат за темою випускної роботи

Содержание

Введення

Розвиток технології та обладнання для обробки металів тиском, а також розширення сортаменту профілів, отриманих при гарячій пластичній деформації з різних марок сталей і сплавів, вимагають безперервного вдосконалення і уточнення методів проектування технологічних процесів і конструкторських розрахунків. Для вирішення цих завдань необхідно вивчення механічних властивостей металів і сплавів за різних температурно-швидкісних умов деформації і розробка достовірних методів їх оцінки в конкретних технологічних процесах для забезпечення максимальної продуктивності устаткування і підвищення якості продукції.

Напруження течії металу є однією з основних складових, яке суттєво впливає на точність розрахунків енергосилових параметрів у процесах обробки металів тиском (ОМТ). Відомо, що напруження течії металу під час гарячої пластичної деформації в основному залежить від ступеня, швидкості та температури деформації. Підвищення ступеня деформації приводить до збільшення напруження течії, тобто до збільшення зміцнення металу. Напруження течії істотно зростає зі збільшенням швидкості деформації металу. З підвищенням температури нагріву всі міцності характеристики металу знижуються.

Тому дослідження існуючих і розробка удосконалених методів напруження течії металу в процесах ОМТ є актуальною роботою

1. Актуальність теми

В технічній літературі, представлені великі експериментальні дані про залежність напруження течії металу σ від міри деформації ε, швидкості деформації u і температури T , представлені у вигляді кривих зміцнення. У ряді випадків, у тому числі і при розробці комп'ютерних програм виникає необхідність в розробці емпіричних формул, які потрібні для розрахунку напруження течії металу σ.Після вибору виду емпіричної формули необхідно визначити константи, що входять в неї, на основі наявної експериментальної інформації по кривих зміцнення. При цьому є два актуальні завдання: забезпечити високу точність визначення σ залежно від ε, u, T на базі кривих зміцнення; виконати науково обґрунтований вибір найбільш раціональних точок в області зміни факторів ε , u , T для визначення відповідних значень σ.

2. Ціль і задачі дослідження

Метою роботи є удосконалення методів розрахунку напруги течії металу, а також розробка нових емпіричних формул та їх аналіз. Поставлені такі завдання:

Основні завдання дослідження:

Розробка нових формул на базі експериментальної інформації, для 44 марок сталей та аналіз їх точності. Аналіз можливості виконання екстраполяції розрахункової інформації.

Об'єктом дослідження є методи розрахунку напруги течії металу в процесах гарячої пластичної деформації.

    3. Вдосконалення методу і розробка емпіричних формул визначення на-пруження течії металу для термомеханічних коефіцієнтів і їх аналіз

    У технічній літературі, представлені великі експериментальні дані про залежність напруги течії металу σ від ступеня деформації ε, швидкості деформації u і температури T, представлені у вигляді кривих зміцнення. У ряді випадків, в тому числі і при розробці комп'ютерних програм виникає необхідність у розробці емпіричних формул, необхідних для розрахунку напруги течії металу σ.[1]

    3.1. Розробка нових формул на базі експериментальної інформації для 44 марок сталей

    Робота є продовженням досліджень , результати які були опубліковані раніше і зокрема пов'язані з магістерською роботою Олексія Пугача.[8] У цих роботах використовували відому експериментальну інформацію σи від ε, u, t.Але не були охоплені відомі графічні залежності для визначення σ у вигляді Кε=f(ε), Кu=f(u), КT=f(Т). Відповідно не існували комп'ютерні програми для обробки такої графічної інформації. Визначення величин σ залежно від довільних значень ε,u,t виконували таким чином [2][3]. На першому етапі у вікно комп'ютерної програми заносяться відскановані графіки (див. рис.1).

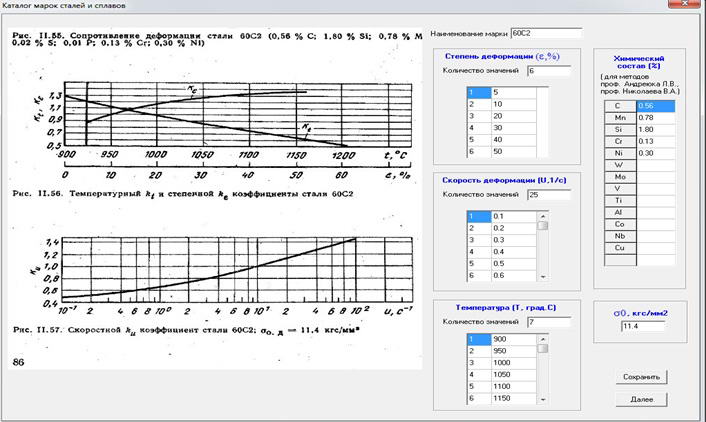
    Вікно вихідної інформації марки

    Рисунок 1 – Вікно вихідної інформації марки

    Потім задаються координати вузлових точок осей в натуральних значеннях для ε,u,t(див. рис.2). При цьому в таблицю автоматично заносяться значення координат вузлових точок в одиницях растрового зображення. Це дозволяє встановити між ними взаємно однозначна відповідність. Аналогічні дії виконуються для кожного з 3-х графіків . Коли сітки задані,переходимо до іншого вікна.

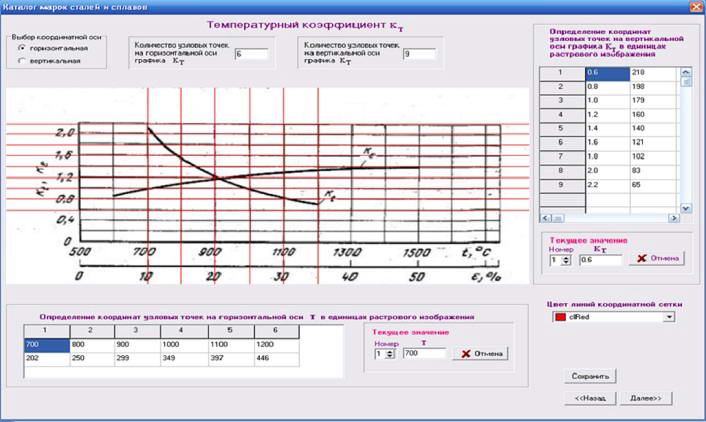
    Вікно побудови координатної сітки

    Рисунок 2 –Вікно побудови координатної сітки

    У наступному вікні виконуємо сплайн - інтерполяцію отриманої інфо-рмації (див. рис.3). Нам необхідно побудувати сплайн криву , відповідну наявної. При цьому потрібно домогтися повного збігу між інтерполяційної кривої і вихідної . На нашому малюнку інтерполяційна крива має бірюзовий колір. Якщо хід вихідної кривої складний , наприклад, є перегини , то сплайн - крива може на першому етапі недостатньо точно лягає на вихідну криву. Тоді можна збільшити число точок і тим самим ми добиваємося повного збігу між цими кривими.

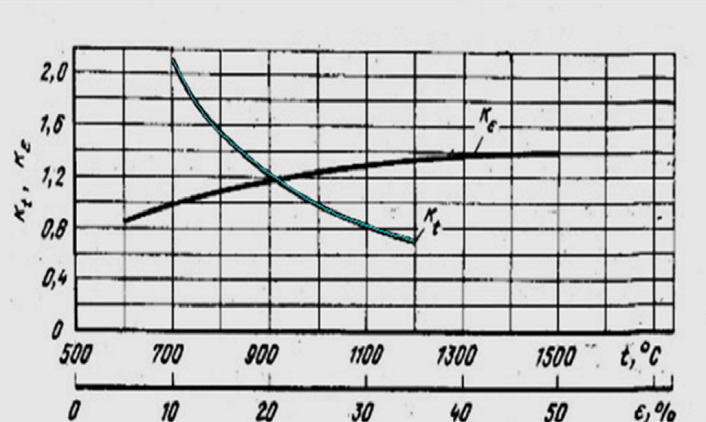
    Вікно зняття експериментальної інформації та побудова сплайн кривих

    Рисунок 3 – Вікно зняття експериментальної інформації та побудова сплайн кривих

    Розраховані у вікні величини напруги течії металу при заданих значеннях ε,u,t автоматично передаються в таблицю, яка і забезпечує точну апроксимацію вихідних кривих (див. рис.4). На базі цієї таблиці в раннє виконаних роботах створена методика розрахунку σ при заданих значеннях ε, u, t.

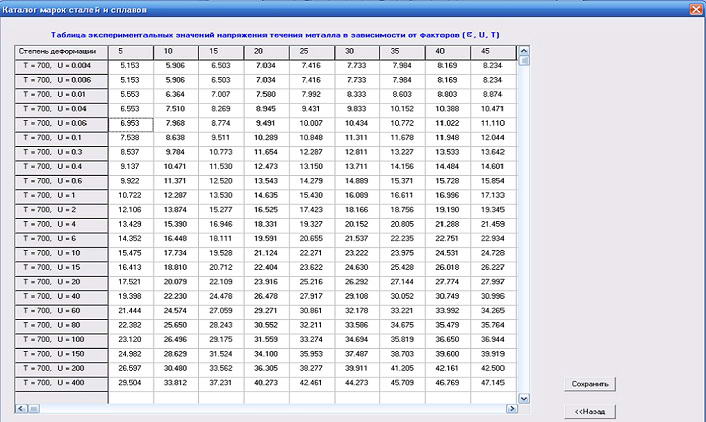
    Значення величин σ при заданих значеннях факторів, отриманих в ході роботи програми

    Рисунок 4 – Значення величин σ при заданих значеннях факторів, отриманих в ході роботи програми

    У це вікно передається з попереднього вікна розглянута раннє таблиця (див. рис.5). Також тут вказуються межі зміни факторів, для яких буде розроблятися формула. Потім натискаємо кнопку далі і переходимо до наступного вікна

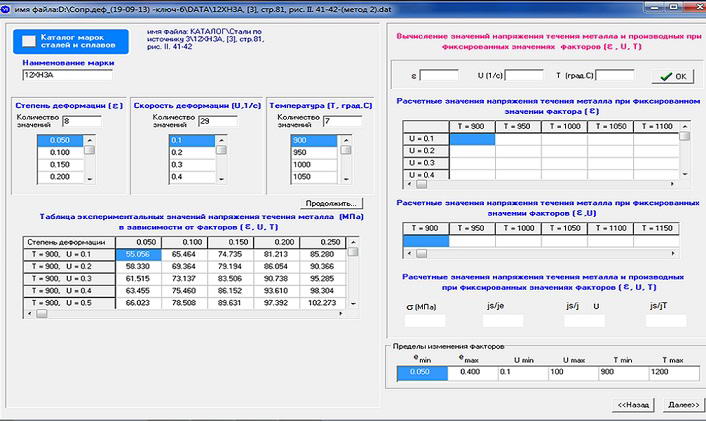
    Вікно розрахунку σ на основі експериментальної інформації

    Рисунок 5 – Вікно розрахунку σ на основі експериментальної інформації

    У це вікно передаються межі зміни факторів ε,u,t. Для науково - обґрунтованого вибору найбільш раціональних точок в області зміни факторів запропоновано застосувати метод планованого розрахункового експерименту [5]. (см. рис.6). У цьому ж вікні формується план - матриця кодових і натуральних значень факторів . У відповідності з теорією планованого експерименту , план матриця для 3-х факторів завжди містить 15 рядків для визначення величин σ.Планований експеримент , охоплює всю задану область зміни факторів і визначає найбільш раціональні точки для визначення величин . Причому це науково - обґрунтований теорією планованого експерименту мінімум дослідів . Для сталі 12ХН3А тут представлені значення напруги течії металу σэксп, по суті отримані шляхом сплайн - інтерполяції кривих зміцнення. На основі методу найменших квадратів автоматично знаходяться константи , що входять у формулу проф. В.І. Зюзіна . Потім на її основі виконується розрахунок величин σр в тих же 15 - ти дослідах.Знайдено середнє відносне відхилення розрахункових значень σр по відношенню до відповідних експериментальними значеннями . Зазначене відхилення дорівнює 1,9 %. Це точність апроксимації .

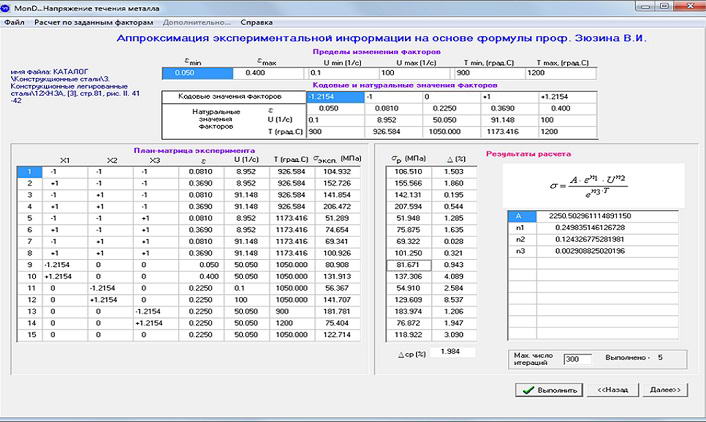
    Вікно розрахунку констант, що входять у формулу проф. Зюзіна В.І.

    Рисунок 6 – Вікно розрахунку констант, що входять у формулу проф. Зюзіна В.І.

    Аналогічно було розроблено вікно програми, що дозволяє визначити константи, що входять до поліном другого ступеня. Вид полінома представлений в правій частині вікна (див. рис.7).Для сталі 12ХН3А представлені значення напруги течії металу σэксп,отримані також шляхом сплайн-інтерполяції кривих зміцнення. Знайдено константи, що входять у формулу полінома другого ступеня, і на їх основі виконано розрахунок величин σр. Знайдена точність апроксимації експериментальних значень σр.Вона дорівнює 7,1%.

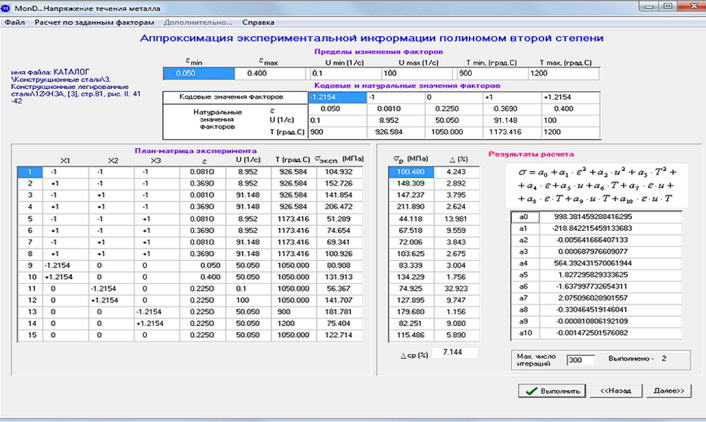
    Вікно розрахунку констант входять до поліном другого ступеня

    Рисунок 7 – Вікно розрахунку констант входять до поліном другого ступеня

    На основі представленого удосконаленого методу виконаний розрахунок констант для 44 марок сталей входять у формулу проф. Зюзіна . [1] Середня відносна помилка апроксимації експериментальної інформації для всіх марок сталей за формулою проф. Зюзіна склала 3,5 %. До цієї роботи було лише 6 аналогічних формул , отриманих на базі експериментальних графічних , представлених залежностей у вигляді Кε=f(ε), Кu=f(u), КT=f(Т). Виконано також розрахунок констант , що входять в представлений поліном другого ступеня. Середня відносна помилка апроксимації експериментальної інформації для всіх 44 -х марок сталей за цією формулою дорівнює 4,8 %.

    Тобто точність на базі представленого полінома висока, але не вище тієї, що дає формула, отримана проф. Зюзіним.

    3.2. Аналіз точності розроблених формул напруги течії металу для конструкційних, інструментальних і нержавіючих марок сталей

    Питання точності отриманих формул розрахунку напруги течії металу залишається актуальним. Новий метод виконання аналізу точності розроблених формул , По перше, пов'язаний з експериментальної інформації , яка не використовувалася при розробці цих формул.[6] По друге , була застосована програма , яка в автоматизованому режимі формує план - матрицю планованого експерименту для даної марки сталі. З лівого боку на малюнку показаний планований експеримент , який виконаний на базі експериментальної інформації , яка використовується для перевірки точності нової формули . З правого боку дана формула яку ми перевіряємо і яку отримали на базі іншої експериментальної інформації.[1] Отримали , що помилка нової формули менше 4%. Точність формул за цією методикою перевірили для 7-ми марок сталей.

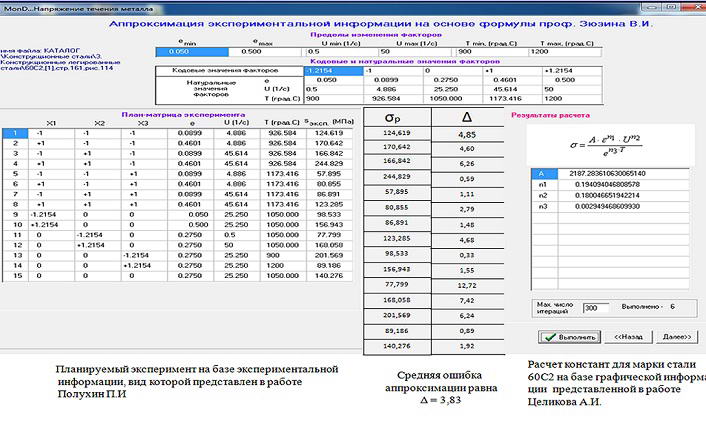
    Аналіз точності розроблених формул напруги течії металу

    Рисунок 8 – Аналіз точності розроблених формул напруги течії металу

    4. Аналіз можливої екстраполяції розрахункової інформації в процесі визначення напруги течії металу

    Далі було поставлено нове завдання про можливість виконання екстраполяції розрахункової інформації на базі розроблених формул . Тобто розрахунку напруги течії металу за отриманими формулами при значеннях ε,u,t, які лежать за тими межами , в яких розроблялася формула . Весь діапазон зміни значень факторів ε,u,t, розбили на дві частини. В інтервалі від 0 до 70% розробляли формулу . А в інтервалі від 80 до 100 % перевіряли точність формули при екстраполяції . Це було можливо виконати так як відповідна експериментальна інформація була на інтервалі від 0 до 100 % по кожному фактору.

    Виконуємо екстраполяцію для марки сталі 4х13

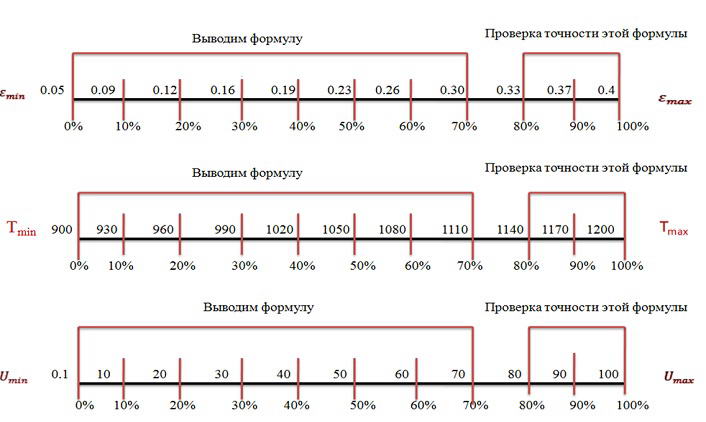
    Аналіз можливої екстраполяції розрахункової інформації

    Рисунок 9 – Аналіз можливої екстраполяції розрахункової інформації

    Формула розроблена в діапазоні від 0 до 70% інтервалу по кожному з 3-х факторів.

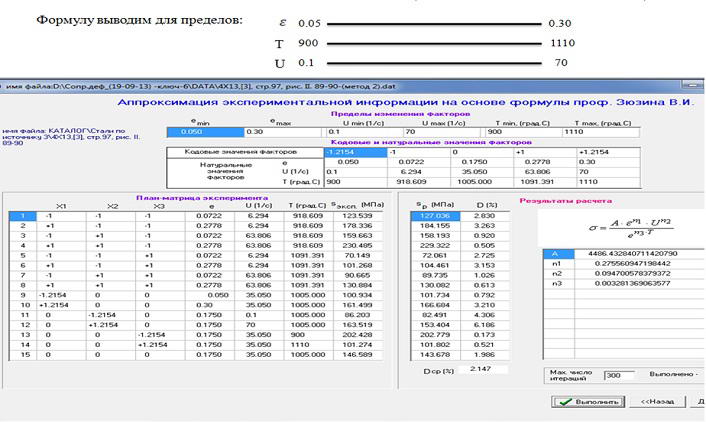
    Аналіз можливої екстраполяції розрахункової інформації

    Рисунок 10 – Аналіз можливої екстраполяції розрахункової інформації

    Виконано перевірку точності розрахунків шляхом екстраполяції в діапазоні від 80 до 100% по кожному фактору. Зліва на рисунке 11 представлена експериментальна інформація. Праворуч результати екстраполяції. Бачимо, що в розглянутому варіанті помилка не перевищує 8%.

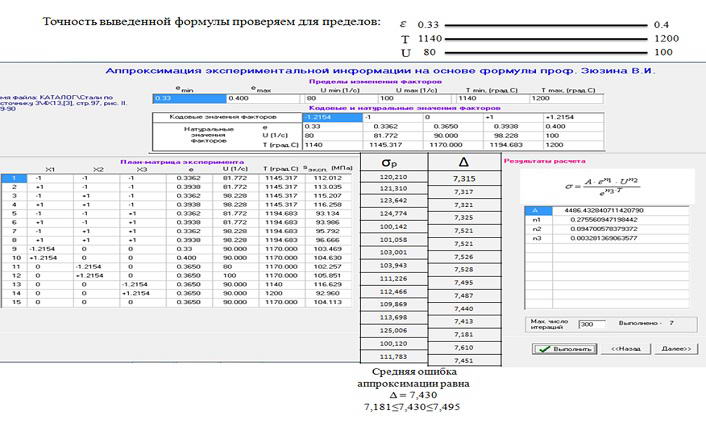
    Аналіз можливої екстраполяції розрахункової інформації

    Рисунок 11 – Аналіз можливої екстраполяції розрахункової інформації

    Висновки

    У роботі створено нові вікна для комп'ютерної програми розробки формул розрахунку напруги течії металу на базі сплайн інтерполяції експериментальних кривих зміцнення і планованого експерименту.Зазначені вікна використовували для отримання формул на базі цифрової інформації по напрузі течією металу залежно від ступеня , швидкості і температури деформації для 44 марок сталей. На основі розробленого методу визначено константи для 44 конструкційних , інструментальних і нержавіючих марок сталей для двох типів формул . Визначено середня відносна помилка апроксимації експериментальної інформації , яка не перевищує 5 %.

    Виконано аналіз точності семи з отриманих формул , при чому по відношенню до експериментальної інформації , яка не використовувалася при їх розробці.Отримано, що середня похибка розрахункових даних по відношенню до експериментальних не перевищує 7 % , а максимальна - 15 %.

    Проведено аналіз можливості екстраполяції розрахункової інформації для марки стали 4Х13 . Середня помилка стосовно експериментальної інформації склала 7,4 %.

    Далі в магістерській роботі планується виконати аналіз можливої екстраполяції розрахункової інформації для різних марок сталей.

      Список джерел

    1. Целиков А.И. Теория прокатки: Справочник / А.И. Целиков, А.Д. Томленов, В.И. Зюзин, А.В. Третьяков, Г.С. Никитин. - М.: Металлургия, 1982. - 335с.
    2. Яковченко А.В. Определение напряжения течения металла с учетом истории процесса нагружения на основе уравнения А.Надаи/ А.В.Яковчеко, Н.И.Ивлева, А.А.Пугач// Наукові праці ДонНТУ. Металургія, 2011.-Вип.12(177). - С.181 - 193.
    3. Яковченко А.В. Анализ точности известных методов расчета напряжения течения металла в зависимости от химического состава стали / А.В. Яковченко, А.А. Пугач, Н.И. Ивлева // Вісник Приазовського державного технічного університету. Сер.: Технічні науки: Зб. наук. праць. – Маріуполь: ДВНЗ «Приазов. держ. техн. ун-т», 2011. - Вип.2(23). - С. 69 - 80.
    4. Данилов А.В. Анализ и усовершенствование методов расчета напряжения течения металла в процессах горячей пластической деформации. Металлургия и обработка металлов (выпуск 12) / Материалы научно-исследовательских работ студентов и молодых ученых физико-металлургического факультета ДонНТУ. – Донецк: ДонНТУ, 2009. – С. 42,43.
    5. Винарский, М.С. Планирование эксперимента в технологических исследованиях : учеб. пособие / М.С. Винарский, М.В Лурье. – К.: Техника, 1975. – 168 с.
    6. Полухин П.И. Сопротивление пластической деформации металлов и сплавов: Справочник / П.И. Полухин, Г.Я. Гун, А.М. Галкин. – М.: Металлургия, 1983. - 352с.
    7. Примение теории ползучести при обработке металлов давлением. Поздеев А.А., Тарновский В.И., Еремеев В.И., Баакашвили В.С. Изд-во «Металлургия», 1973, 192с.
    8. Пугач А.А.Совершенствование метода получения расчетных эмпирических формул для расчета напряжения течения металла.Металлургия и обработка металлов/ Материалы Всеукраинской научно-практической конференции студентов. - Донецк: ДонНТУ, 2012. - 209 с. - С. 56 - 57.