Українська   Русский
DonNTU   Masters' portal

Abstract

Content

Introduction

Development of technology and equipment for metal forming as well as expanding assortment of profiles obtained during hot plastic deformation of different types of steels and alloys, require continuous improvement and refinement of methods of designing processes and design calculations. To solve these problems it is necessary to study the mechanical properties of metals and alloys at different temperature and strain rate conditions and the development of reliable methods for their evaluation in specific processes to maximize equipment performance and product quality improvement.

Flow stress of the metal is one of the main of the constituent, which significantly affects the accuracy of calculations of the energy-power parameters in metal forming processes. It is known that the flow stress of the metal during the hot plastic deformation is mainly dependent on the degree of temperature and strain rate. Increasing the degree of deformation increases the flow stress, that is to increase the hardening of the metal. Flow stress increases significantly with increasing strain rate metal.

Therefore, studies of existing and development of improved methods for calculating the flow stress of the metal in the metal forming processes is an urgent work.

1. Relevance of the topic

An urgent task is to obtain empirical formulas for calculating the flow stress of metal for construction, tool and stainless steels based on the available experimental information. Analysis of the accuracy of the formulas developed in the flow stress of the metal.

2.The purpose and objectives of the study

The aim is to improve methods of calculating the flow stress of the metal, as well as the development of new empirical formulas and analysis.

Main tasks of the research:

Development of new formulas based on experimental data for 44 grades and analysis of their accuracy. Analysis of possible extrapolation calculation data

Object of research are methods for calculating the flow stress of the metal during hot plastic deformation.

    3. Improvement of the method and the development of empirical formulas of determination the flow stress for thermomechanical coefficients

    At the present time in the technical literature, there are extensive experimental data on the flow stress of the metal from the σ strain ε, strain rate u and temperature T, presented in the form of hardening curves. In several cases, including the development of computer programs is necessary to develop empirical formulas, which are necessary for the calculation of the flow stress of metals σ.[1]

    3.1. Development of new formulas on the base of experimental information for 44 grades of steel

    Work is continuation of researches, the results of which were published earlier and in particular linked to the master's work Alexei Pugach. [8] In these works were not covered by the famous graphic dependencies to determine σ in the form of Кε=f(ε), Кu=f(u), КT=f(Т). Respectively there were no computer programs for processing of such graphic information. Determination of the quantities σ, depending on the arbitrary values of ε, U, T invited to perform as follows. In the first stage of the window a computer program recorded the scanned curves of hardening (Fig. 1).

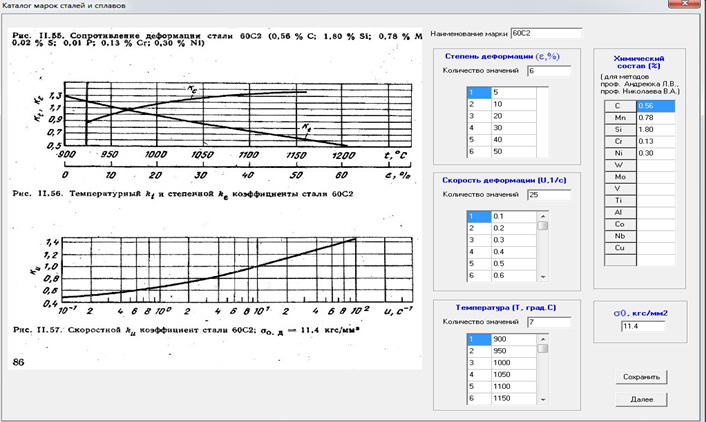
    Window background information

    Figure 1 – Window background information

    Then coordinates of nodal points are set in natural values for ε,u,t(Fig. 2). In the table are automatically recorded the coordinates of nodal points in terms of the bitmap. This allows you to set between one correspondence. Similar actions are performed for each of the 3 graphs. When grids are set, we pass to other window.

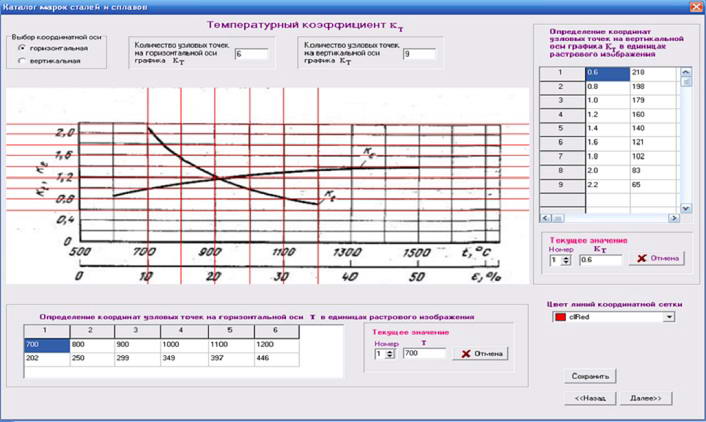
    Window of creation of a coordinate grid

    Figure 2 – Window of creation of a coordinate grid

    In the following window we carry out a spline interpolation of received information (Fig. 3). Thus it is necessary to achieve full coincidence between an interpolation curve and initial. In our drawing the interpolation curve has turquoise color. If the initial course of the hardening curve is rather complicated, for example, there are excesses and spline - curve is not accurately placed on the original curve, it is possible to increase the number of points and achieve a complete coincidence of the interpolation curve and the original one.

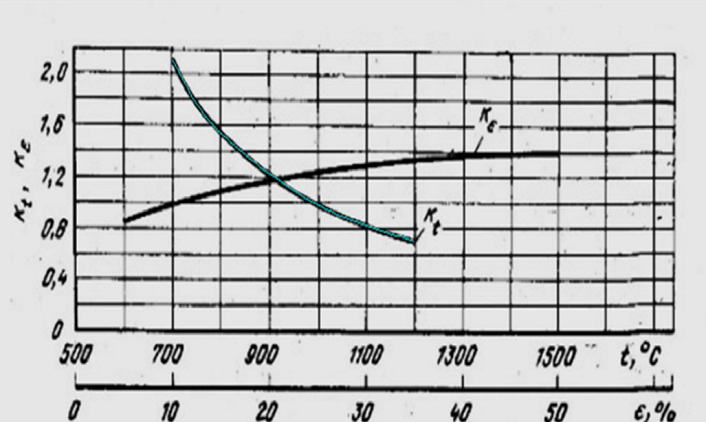
    Window removal of experimental data and the construction of spline curves

    Figure 3 – Window removal of experimental data and the construction of spline curves

    Calculated in the magnitude of the flow stress of the metal for the given values ε,u,t is automatically transferred to the table, which provides an accurate approximation of the original curves (Fig. 4).On the basis of this table in the work performed previously established method of calculation σ for given values of ε, u, t.

    Value σ for given values of the factors obtained in the course of the program

    Figure 4 – Value σ for given values of the factors obtained in the course of the program

    This dialog box is transferred from the previous table (Fig. 5). Also, specifies the range of variation of the factors which will be developed formula. Then click next and proceed to the next window.

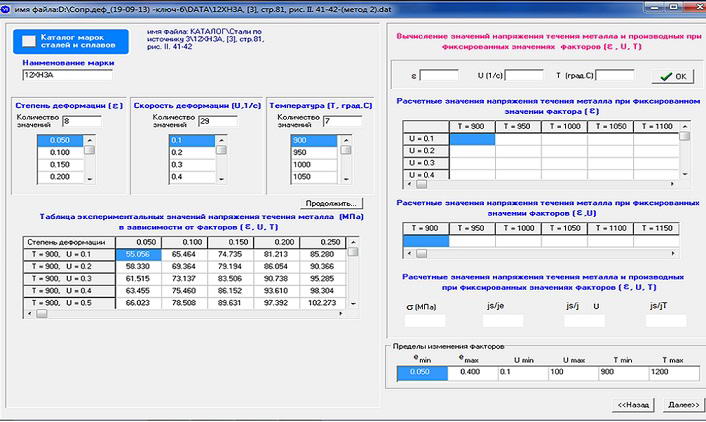
    Calculation window σ on the basis of experimental information

    Figure 5 – Calculation window σ on the basis of experimental information

    For scientific a reasonable choice of the most rational points in the field of change of factors ε, u, t is offered to apply a method of planned settlement experiment. [5].Created window (see Figure 6) where a table located in the upper part, passed the limits of variation factors ε, U, T. In the same window formed a table of code values and natural factors. In accordance with the theory of planned experiment, the plan is the matrix for the 3 factors ε, U, T always contains 15 lines to determine the values of σ. The planned experiment covers the entire range of the factors ε, U, T, and determines the most rational point for determining the values of σ on the basis of experimental data. And it is a science-based theory of planned experiment a minimum of experiments. To become 12ХН3А shows the values of the flow stress of the metal σэксп obtained by spline interpolation curves of hardening. Under the proposed method are found in the constant in the formula of Professor. V.I. Zyuzin and on this basis calculated the values of σр. The values of the constants are presented in the right pane, calculated by the method of least squares. Also found an average relative deviation of calculated values of gp, from the corresponding experimental values σэксп equal to 1.9%.

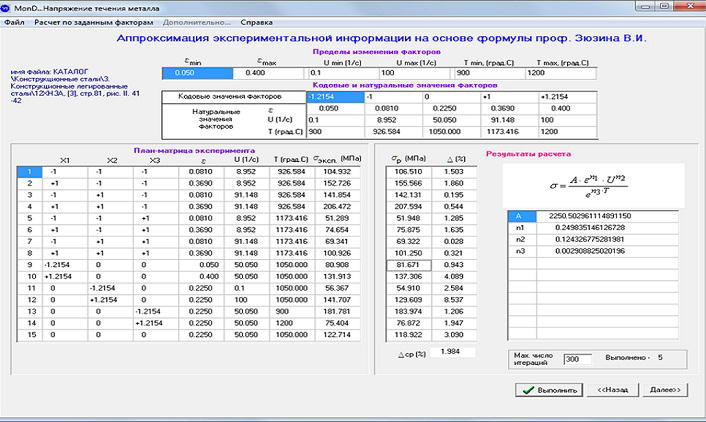
    Windows program for calculation of the constants in the formula V.I. Zyuzin

    Figure 6 – Windows program for calculation of the constants in the formula V.I. Zyuzin

    Similarly, we developed the program window, indicating constants in the second degree polynomial. Form of a polynomial is presented in the right part of the window (see Figure 7). Steel 12HN3A shows the values of the flow stress of the metal σэксп also derived by spline interpolation of the hardening curves. Found constants in the second-degree polynomial formula, and based on them have been calculated values σр. Found the accuracy of approximation of the experimental values σэксп. It is equal to 7.1%

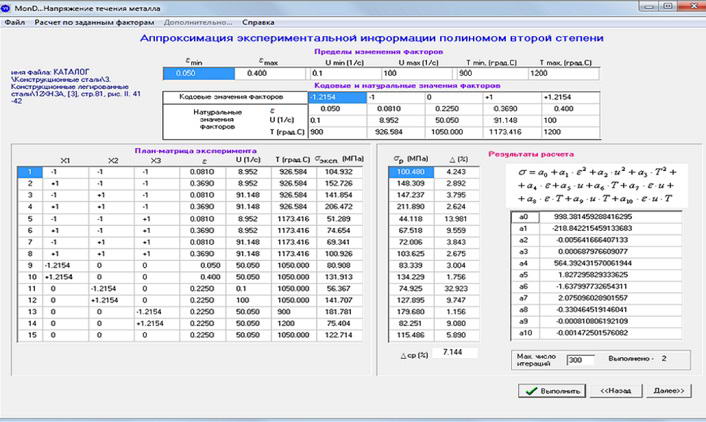
    Window of calculation of constants entering a polynom of the second degree

    Figure 7 – Window of calculation of constants entering a polynom of the second degree

    Also performed a calculation of the constants appearing in the submitted second-degree polynomial. The average relative error of approximation of experimental data for all 44 grades of this formula is 4.8%.

    That is on the basis of the given polynom high, but not above that that the formula received by the prof. Zyuzin gives accuracy.

    3.2. Analysis of exactness of the worked out formulas of determination the flow stress for structural, tool, stainless steels grades

    Question the accuracy of the formulas for calculating the flow stress of the metal remains relevant . New execution method to analyze the accuracy of the formulas developed , first , associated with experimental data , which is not used in the development of these formulas Second, was applied program which generates automated plan matrix planned experiment for this grade of steel [6]. On the left side of the figure shows the planned experiment, which was carried out on the basis of experimental data , which is used to check the accuracy of the new formula . On the right side gave the tested formula that got the other on the basis of experimental information.[1]. . We have shown that the new formula error less than 4% . Accuracy formulas tested by this method for 7-steels.(see Figure 8).

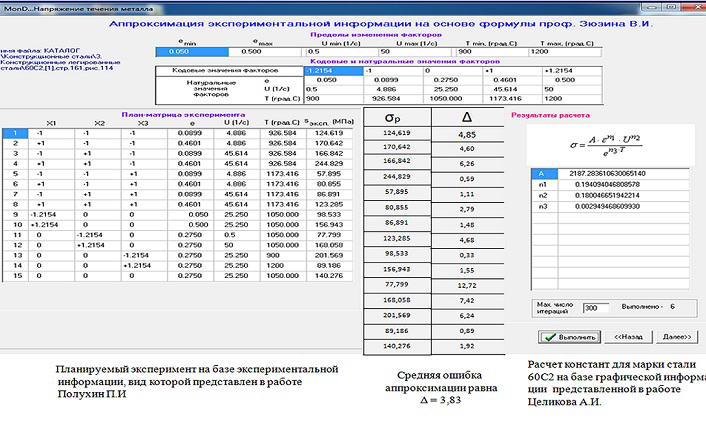
    Analysis of the accuracy of the formulas developed in the flow stress of the metal

    Figure 8 – Analysis of the accuracy of the formulas developed in the flow stress of the metal

    4. Analysis of possible extrapolation calculation data in the process of determining the flow stress of the metal

    Next was a new task for the possibility of the extrapolation of the estimated information based on the developed formulas. That is, the calculation of the flow stress of the metal on the derived formulas for values of ε, u, t, which lie outside of those in which the formula was developed . The entire range of variation factor values ε, u, t broke into two parts. In the range from 0 to 70% of developed formula. A range of 80 to 100% accuracy checked by extrapolation formula . It was possible to perform because Experimental corresponding information was in the interval from 0 to 100 % for each factor (see Figure 9).

    We carry out extrapolation for steel 4Х13

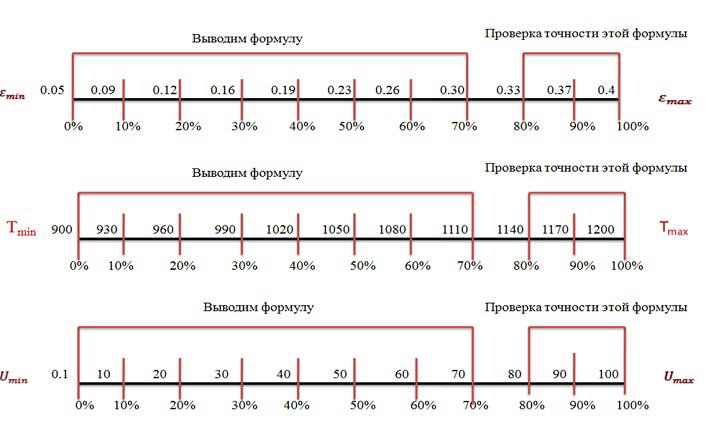
    Analysis of possible extrapolation calculation data

    Figure 9 – Analysis of possible extrapolation calculation data

    The formula developed in the range of from 0 to 70% for each interval of 3 factors.

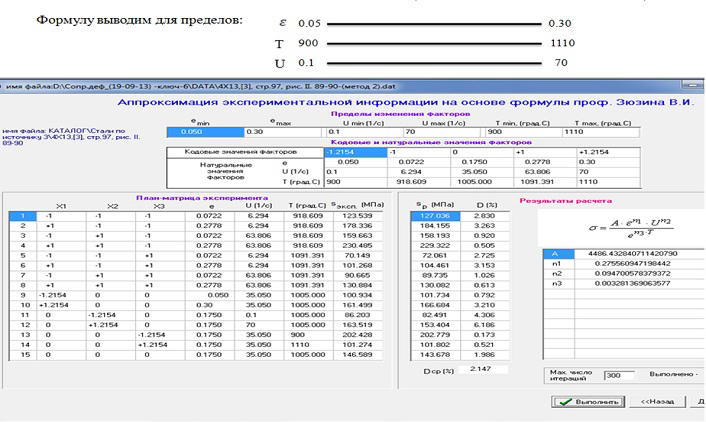
    Analysis of possible extrapolation calculation data

    Figure 10 – Analysis of possible extrapolation calculation data

    Check of accuracy of calculations by extrapolation in the range from 80 to 100% on each factor is executed. Left shows the experimental information. To the right results of extrapolation. See that in the considered variant error does not exceed 8%.

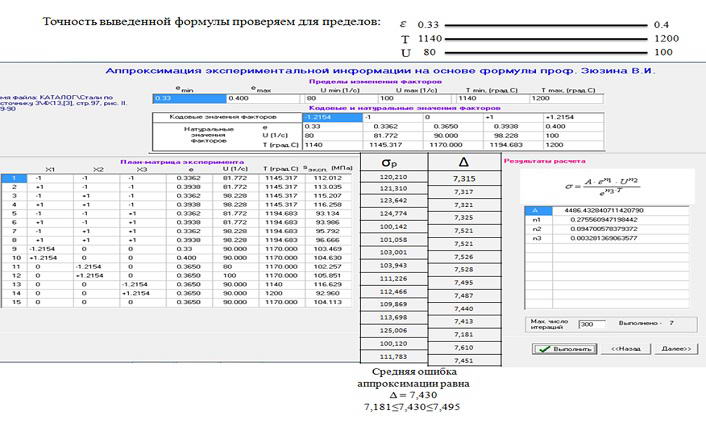
    Analysis of possible extrapolation calculation data

    Figure 11 – Analysis of possible extrapolation calculation data

    Conclusion

    In work new windows for the computer program of development of formulas of calculation of tension of a current of metal on base a spline of interpolation of experimental curves of hardening and planned experiment are created. The specified windows used for receiving formulas on the basis of digital information on tension to a metal current depending on degree, speed and deformation temperature for 44 brands of the staly. On the basis of the developed method constants for 44 constructional, tool and corrosion-proof brands staly for two types of formulas are defined. The average relative error of approximation of experimental information which doesn't exceed 5% is defined.

    An accuracy of the seven formulas obtained than with respect to the experimental data, which was not used in their design. It was found that the average error of the calculated data with respect to the experimental does not exceed 7%, and the maximum - 15%.

    The analysis of possible extrapolation calculation data for steels 4H13. The average error with respect to the experimental data was 7.4%.

    Further to the master's work is scheduled to perform the analysis of possible extrapolation calculation data for different types of steels.

      List of sources

    1. Целиков А.И. Теория прокатки: Справочник / А.И. Целиков, А.Д. Томленов, В.И. Зюзин, А.В. Третьяков, Г.С. Никитин. - М.: Металлургия, 1982. - 335с.
    2. Яковченко А.В. Определение напряжения течения металла с учетом истории процесса нагружения на основе уравнения А.Надаи/ А.В.Яковчеко, Н.И.Ивлева, А.А.Пугач// Наукові праці ДонНТУ. Металургія, 2011.-Вип.12(177). - С.181 - 193.
    3. Яковченко А.В. Анализ точности известных методов расчета напряжения течения металла в зависимости от химического состава стали / А.В. Яковченко, А.А. Пугач, Н.И. Ивлева // Вісник Приазовського державного технічного університету. Сер.: Технічні науки: Зб. наук. праць. – Маріуполь: ДВНЗ «Приазов. держ. техн. ун-т», 2011. - Вип.2(23). - С. 69 - 80.
    4. Данилов А.В. Анализ и усовершенствование методов расчета напряжения течения металла в процессах горячей пластической деформации. Металлургия и обработка металлов (выпуск 12) / Материалы научно-исследовательских работ студентов и молодых ученых физико-металлургического факультета ДонНТУ. – Донецк: ДонНТУ, 2009. – С. 42,43.
    5. Винарский, М.С. Планирование эксперимента в технологических исследованиях : учеб. пособие / М.С. Винарский, М.В Лурье. – К.: Техника, 1975. – 168 с.
    6. Полухин П.И. Сопротивление пластической деформации металлов и сплавов: Справочник / П.И. Полухин, Г.Я. Гун, А.М. Галкин. – М.: Металлургия, 1983. - 352с.
    7. Примение теории ползучести при обработке металлов давлением. Поздеев А.А., Тарновский В.И., Еремеев В.И., Баакашвили В.С. Изд-во «Металлургия», 1973, 192с.
    8. Пугач А.А.Совершенствование метода получения расчетных эмпирических формул для расчета напряжения течения металла.Металлургия и обработка металлов/ Материалы Всеукраинской научно-практической конференции студентов. - Донецк: ДонНТУ, 2012. - 209 с. - С. 56 - 57.