Abstract
Content
- Introduction
- 1. Relevance of the topic
- 2. Development of mathematical model for estimating the survivability of 0.4 / 0.22 kV load nodes
- 2.1 Problem statement in mathematical form.
- 2.2 Application of the theory of homogeneous Markov processes for solving a problem.
- 2.3 Determination of the average time before the loss of life of the load node and the dispersion of this time.
- Conclusions
- List of sources
Introduction
The concept of vitality is known in the art for a long time and is practically used in the creation of technical systems for various purposes. Until now no unified theory has been created that would unite the main provisions and concepts of the theory of the durability of the object, which does not allow to design practical recommendations for ensuring the durability of complex systems at the design stage.
At the same time, the problem of vitality continues to remain one of the main for modern technology. This is explained by the fact that the tasks that are being solved continuously are complicated and the requirements for reliability of their fulfillment are increased at the same time.
In recent years, there has been a significant increase in the interest in this characteristic, both in the theoretical and practical terms, in connection with the increase in the damage from the long shutdown of even part of the system, and an increase in the share of technologically related violations of workability, and, consequently, the scale of "damage" of the system .
1. Relevance of the topic
The complexity of the systems goes in various industries. On the one hand, an increasing number of component elements is included in the technical systems, on the other hand, their structure becomes more complex, which determines the combination of individual elements and their interaction in the process of functioning and maintenance of work capacity.
A system consisting of a large number of component elements and having a complex structure of functioning requires the development of special methods for ensuring, enhancing and maintaining the survivability of such systems, including the development of mathematical methods.
The desire to reduce the damage to the system at the same time is the desire to create more favorable conditions for the restoration of the required level of functioning. In addition, due to the developed connections between different systems and subsystems on different channels (informational, material, energy), secondary role of the violations of the working capacity of the elements of the system can play a significant role. Damage from secondary damage can be no less than from the primary, up to the termination of the system.
In this regard, it is necessary to systematize the basic methods and approaches to assess the survivability of power supply systems, in particular, for the load cells supplying the end user.
2. Purpose and tasks of the research, planned results
2.1 Problem statement in mathematical form.
ÂAn electrician under the durability of an object is understood as a property to resist perturbations, not allowing their cascading development with a massive disruption of consumers' nutrition [1]. The survivability of the load node will be the ability of consumers and their automatic means to protect themselves from perturbations that can lead to emergency shutdown. The survivability of the load cell depends on the structure of the power supply system and its configuration, the reliability of the electrical equipment, the means of the RZ and emergency automatics, as well as the qualifications of its servicing personnel, the reserve of stability, the reserve of active power.
In the case of a short circuit in the elements of the network and failure in the operation of a number of protective switching devices through which the through-pass emergency current passed, so-called chain accidents occur. Their share accounts for 90% of the damage done to consumers of electric energy. The degree of disruption of the functioning of the installations during accidents and violations in work is called depth. The depth of the chain crash depends on the location of the CF and the number of disconnected switching devices, through which the through-current emergency current flowed and activated their current protection. The depth of the chain failure can be characterized by the number of false dropped intact consumers (sections of tires) or their losses, which are associated with lack of electricity, equipment downtime and technological cycle disorders.
Protective devices (automatic circuit breaker, RCD) belong to the class of duty systems having two operating modes: an alarm mode, a fraction of a second or several seconds, and a standby (standby) mode - hundreds of hours. In the first mode, the device must be triggered, in the second mode it is ready to be triggered but not triggered. [2].
Two kinds of failures of protective devices should be distinguished: failure of the device if there is an appropriate influence on the input (trip failure) and the device is triggered in the absence of influence (false, unnecessary triggers). [3].
The consequences of breaking the reliability of the selectivity and reliability of the protective switching device are different. The false triggering of the protective switching device results in the de-energization of the consumers of the premises during the repeated (manual or automatic) switch-on of the security device.
The random time interval between adjacent CFs in the zone of operation of the protective switching device will be denoted by ![]() , and the time of the existence of the short circuit (the time of the trip of the protection will be considered as a random variable) through
, and the time of the existence of the short circuit (the time of the trip of the protection will be considered as a random variable) through ![]() .
.
We denote by ![]() a random time interval between failures of a protective switching device. The casual time of finding a protective switching device in an undetected denied state is denoted by
a random time interval between failures of a protective switching device. The casual time of finding a protective switching device in an undetected denied state is denoted by ![]() Random Size
Random Size ![]() depends on the reliability of the elements of the protective device, periodic monitoring of its working capacity and qualifications of the personnel.
depends on the reliability of the elements of the protective device, periodic monitoring of its working capacity and qualifications of the personnel.
At random coincidence of independent random intervals of time ![]() è
è ![]() there is a loss of vitality of 0.4 kV load nodes caused by a short circuit.
there is a loss of vitality of 0.4 kV load nodes caused by a short circuit.
Change the state of the protected network in time as a random function n (t), which can take two values: "0" and "1". The state of "0" - in the protected network there are no damages leading to a short circuit. The state of "1" - in the protected network, there was a shortfall.
The sequence of alternating intervals of time between the QZ is denoted by ![]() , and the duration of the existence of the short circuit (the duration of the trip switch of the protective switching device) - through
, and the duration of the existence of the short circuit (the duration of the trip switch of the protective switching device) - through ![]() .
.
All sizes ![]() have a distribution:
have a distribution: ![]() ; and everything
; and everything ![]() - distribution
- distribution ![]() .
.
Size  - the average time interval between the occurrence of a CP in a protected network;
- the average time interval between the occurrence of a CP in a protected network;  - the average time of existence of a short-circuit current (or the mean time of operation of the protective switching device).
- the average time of existence of a short-circuit current (or the mean time of operation of the protective switching device).
Values ![]() and
and ![]() are mutually independent. Transitions from the state of "0"> "1" and "1"> "0" occur instantaneously without time delay.
are mutually independent. Transitions from the state of "0"> "1" and "1"> "0" occur instantaneously without time delay.
The state of the protective switching apparatus is described by a similar function E (t), which can take two values: "0" and "1". The state "0" means that the protective switching device is in operational condition, and "1" - in the scheme of maximum current protection there is damage. Sequence of alternating random intervals of time ![]() reflects the working state of the circuit, and the sequence
reflects the working state of the circuit, and the sequence ![]() - inoperable.
- inoperable.
Let it be all ![]() have the same distribution
have the same distribution ![]() and everything
and everything ![]() - distribution
- distribution ![]() .
.
Values  - average time interval between failures in the operation of the protective switching device;
- average time interval between failures in the operation of the protective switching device;  - average time of finding a protective switching device in an undetected failed state.
- average time of finding a protective switching device in an undetected failed state.
Values ![]() è
è ![]() are mutually independent. Transitions from the state of "0"> "1" and "1"> "0" occur instantaneously without time delay.
are mutually independent. Transitions from the state of "0"> "1" and "1"> "0" occur instantaneously without time delay.
Exponential model of time intervals distribution ![]() and
and ![]() is badly confirmed in practice, however, similar to the way it was done in the works [4], if the intervals between the failures
is badly confirmed in practice, however, similar to the way it was done in the works [4], if the intervals between the failures ![]() è
è ![]() have an exponential distribution law and the probability distribution function of random variables
have an exponential distribution law and the probability distribution function of random variables ![]() è
è ![]() have the following properties:
have the following properties:
1. Random quantities have no non-zero mathematical value:
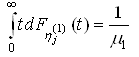 ;
;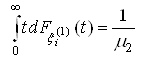 ;
;2. Random variables have a finite second moment:
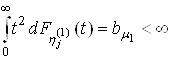 ;
;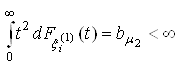 ;
;3. Class of functions ![]() è
è ![]() It is obtained from one function by changing the scale on the abscissa:
It is obtained from one function by changing the scale on the abscissa:
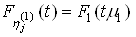 ;
;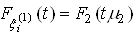 ;
;Then the intensity of the loss of vitality does not depend on the functions of the probability distribution of the random variables at all ![]() è
è ![]() , and is determined only by the mean values of d1 and d2.[6].
, and is determined only by the mean values of d1 and d2.[6].
The loss of the vitality of the load unit 0.4kV comes at the moment of the process's meeting ![]() in state 1, i.e. when the protective switching device (due to its failure) can not disconnect the short-circuit current which appeared in the protected zone accidentally (Fig. 1).
in state 1, i.e. when the protective switching device (due to its failure) can not disconnect the short-circuit current which appeared in the protected zone accidentally (Fig. 1).
The task is to know the process parameters ![]() determine: the average time before the loss of life of the load cell 0.4kV
determine: the average time before the loss of life of the load cell 0.4kV ![]() dispersion of this time
dispersion of this time ![]() , the probability of finding a system in each of the possible states
, the probability of finding a system in each of the possible states ![]() , the probability of loss of durability of the load unit 0.4kV. Q (t)
, the probability of loss of durability of the load unit 0.4kV. Q (t)
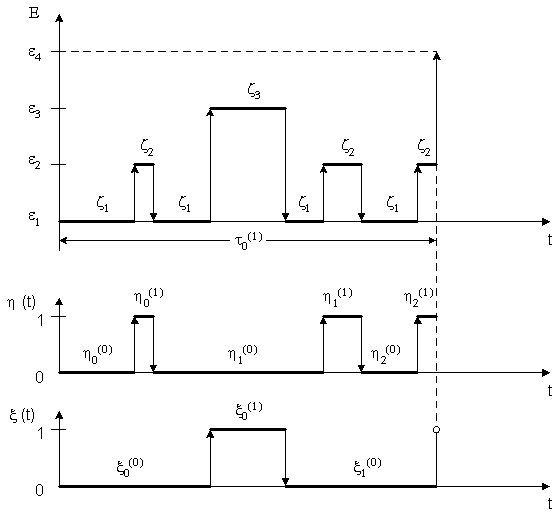
Figure 1 - Possible implementation of the random Markov process with discrete states and continuous time:
![]() - state of the system;
- state of the system;
![]() - random processes;
- random processes;
![]() ,
, ![]() - time of finding the protected network in safe condition and average time of operation of the protective switching device, respectively;
- time of finding the protected network in safe condition and average time of operation of the protective switching device, respectively;
![]() ,
, ![]() - time of finding a protective switching device in faultless and failed states respectively.
- time of finding a protective switching device in faultless and failed states respectively.
2.2 Application of the theory of homogeneous Markov processes to solve a problem.
On the statistical nature of random functions ![]() suppose the following. Probability of transitions for a function
suppose the following. Probability of transitions for a function ![]() from a safe state to a dangerous time span
from a safe state to a dangerous time span ![]() is equal
is equal ![]() , and the transition from a dangerous state to a safe one -
, and the transition from a dangerous state to a safe one - ![]() , ãäå
, ãäå ![]() means that occurrence in the interval of time
means that occurrence in the interval of time ![]() More than one dangerous (safe) state is an infinitesimal small quantity of higher order than the other values. Values
More than one dangerous (safe) state is an infinitesimal small quantity of higher order than the other values. Values ![]() and
and ![]() are process parameters
are process parameters ![]() . Parameter
. Parameter ![]() characterizes the frequency or speed at which safe states change to dangerous, and
characterizes the frequency or speed at which safe states change to dangerous, and ![]() characterizes the frequency or speed at which hazardous states change to safe ones.
characterizes the frequency or speed at which hazardous states change to safe ones.
For a function ![]() the probability of passing from a safe state to a dangerous time
the probability of passing from a safe state to a dangerous time ![]() is equal
is equal ![]() , and the reverse transition is carried out with probability
, and the reverse transition is carried out with probability ![]() .
.
Parameter ![]() characterizes the rate of change of safe intervals of time to dangerous, and
characterizes the rate of change of safe intervals of time to dangerous, and ![]() - the speed of changing dangerous times to safe. Accepted assumptions mean that
- the speed of changing dangerous times to safe. Accepted assumptions mean that ![]() can be considered as two Markov processes with two states: "0" - safe, "1" - dangerous.
can be considered as two Markov processes with two states: "0" - safe, "1" - dangerous.
Loss of vitality in this description comes at the moment of the process ![]() in state 1, that is, when
in state 1, that is, when ![]() .
.
We will assume that at the initial moment of time ![]() , that is, the protective switching device is functioning well and is in standby mode; There is no short circuit in the protected network.
, that is, the protective switching device is functioning well and is in standby mode; There is no short circuit in the protected network.
The set of processes ![]() consider one Markov process
consider one Markov process ![]() with 4 discrete states and continuous time. The system at any time t can be in one of a finite set of states:
with 4 discrete states and continuous time. The system at any time t can be in one of a finite set of states:
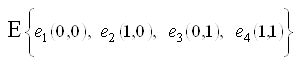 ,
,Where, ![]() - âthe protected network does not have a short circuit, the protective switching device is operational and is in the "waiting" mode;
- âthe protected network does not have a short circuit, the protective switching device is operational and is in the "waiting" mode;
![]() - a protected circuit occurred in the protected network, the protective switching device is working properly and ready to disconnect the current of the short circuit;
- a protected circuit occurred in the protected network, the protective switching device is working properly and ready to disconnect the current of the short circuit;
![]() - in the protected network there is no short circuit, the protective switching device is in a failed state;
- in the protected network there is no short circuit, the protective switching device is in a failed state;
![]() - a short circuit occurred in the protected network, the protective switching device is in a failed state.
- a short circuit occurred in the protected network, the protective switching device is in a failed state.
When accidentally hit the system in a state ![]() A load cell of 0.4 kV loses its survivability.
A load cell of 0.4 kV loses its survivability.
We denote by ![]() the probability that the system will be in a small amount of time
the probability that the system will be in a small amount of time ![]() will remain in a position
will remain in a position ![]() ,
, ![]() and through
and through ![]() - the probability that the system is in time
- the probability that the system is in time ![]() will move from the state
will move from the state ![]() into a state
into a state ![]() ,
, ![]() ,
, ![]() . These probabilities of transitions are defined as follows:
. These probabilities of transitions are defined as follows:
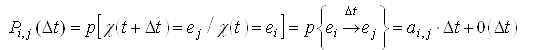 ; (1)
; (1)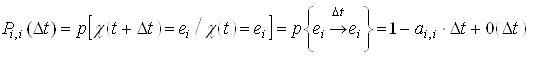 . (2)
. (2)In formula (1) the value is ![]() takes into account, to the accuracy of the terms of the second order of smallness, that over time
takes into account, to the accuracy of the terms of the second order of smallness, that over time ![]() the system will move from the state
the system will move from the state ![]() in a different state
in a different state ![]() , and in the formula (2) the value
, and in the formula (2) the value ![]() takes into account, to the accuracy of the terms of the second order of smallness, that over time
takes into account, to the accuracy of the terms of the second order of smallness, that over time ![]() there will not be a transition of the system from the state
there will not be a transition of the system from the state ![]() in any other state, that is, the process will remain in a state
in any other state, that is, the process will remain in a state ![]() .
.
We denote by ![]() ,
, ![]() time of the process being in a state
time of the process being in a state ![]() . For a regular homogeneous Markov process, the distribution of random variables
. For a regular homogeneous Markov process, the distribution of random variables ![]() does not contradict the exponential probability distribution function [5]:
does not contradict the exponential probability distribution function [5]:
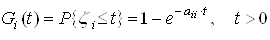 . (3)
. (3)Regular homogeneous Markov process with discrete states and continuous time ![]() The bilinearity is determined if the distribution (3) and the transition probability matrix are known
The bilinearity is determined if the distribution (3) and the transition probability matrix are known ![]() :
:
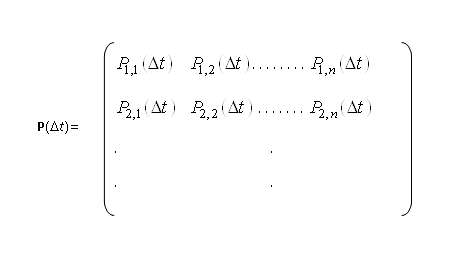 . (4)
. (4)The matrix (4) is square with non-negative elements, and the sum of the elements in each row is 1. [7].
Using formulas (1) and (2), we determine the probability of a system being located in time ![]() in the state of "0"
in the state of "0" ![]() , probability of transition in time
, probability of transition in time ![]() from the state of "1" to "0"
from the state of "1" to "0" ![]() , probability of finding the system time
, probability of finding the system time ![]() in the state of "1"
in the state of "1" ![]() , probability of transition in time
, probability of transition in time ![]() from state "0" to "1" state
from state "0" to "1" state ![]() :
:
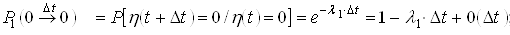 ;
;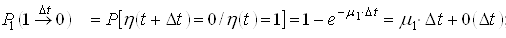 ;
;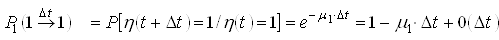 ;
;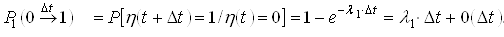 .
.The protective switching device can also be in two states: "0" is a safe state, the protective switching device is in the "standby" mode; The state "1" - the protective switching device is in a dangerous (failed) state.
Using formulas (1) and (2) we find the probabilities of transitions for a protective switching device over time ![]() :
:
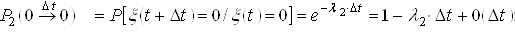 ;
;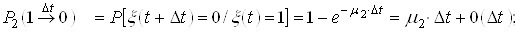 ;
;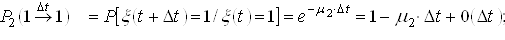 ;
;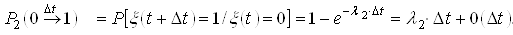 .
.We define the probabilities of transitions for a system described by a set of two random functions ![]() :
:
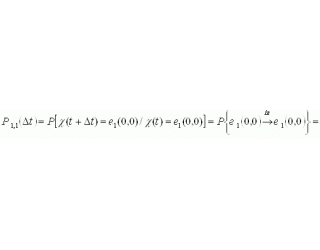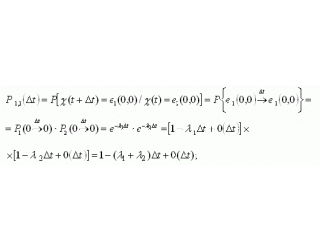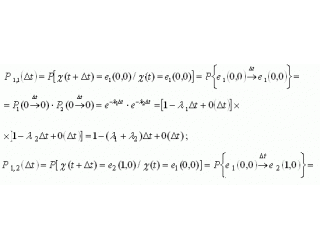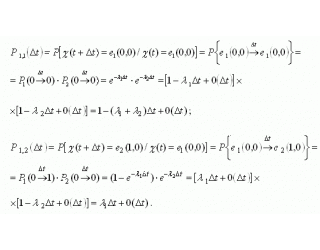
where ![]() means that two transitions over time
means that two transitions over time ![]() there is an infinitely small quantity:
there is an infinitely small quantity:
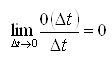 .
.2.3 Determination of the average time before the loss of life of the load node and the dispersion of this time.
The probabilities of staying in each of the possible failure states are determined from the system of linear differential equations:
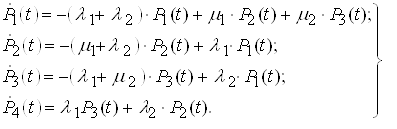 .(5)
.(5)System (5) is solved under initial conditions  .
.
The probability of loss of vitality by the 0.4kV load node is as follows:
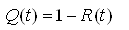 ,
,where  ,
,
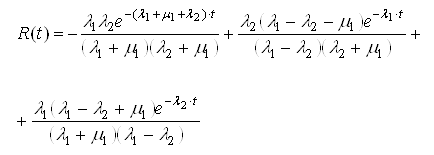 .
.The probability of loss of the survivability of the load node during time t:
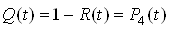 .
.Average time ![]() before the loss of survivability of the fire load node can be determined by the formula:
before the loss of survivability of the fire load node can be determined by the formula:
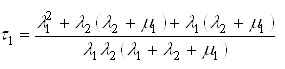 .
.Dispersion of time ![]() can be determined using the expression:
can be determined using the expression:
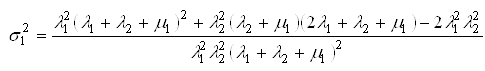 .
.In case the condition is fulfilled ![]() , then:
, then:
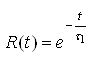 .
.The indicator of survivability can be the frequency of occurrence of system chain accidents with different depth of disturbance of electric supply:
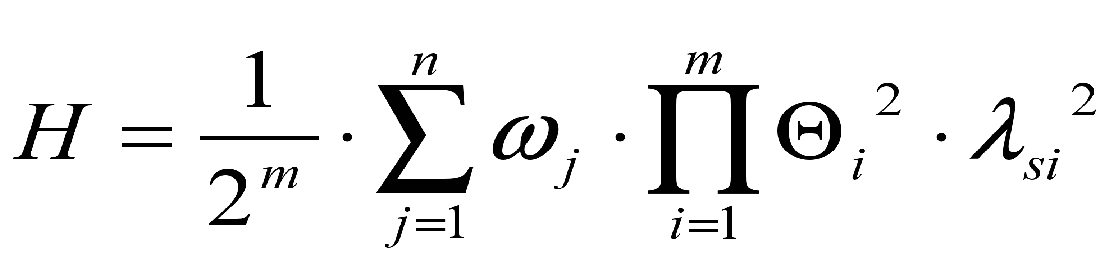 .
.where ![]() - the parameter of the flow of independent CFs in the jth element of the network;
- the parameter of the flow of independent CFs in the jth element of the network;
![]() - the parameter of the fail flow in the operation of the protective switching device;
- the parameter of the fail flow in the operation of the protective switching device;
![]() - time interval between system diagnostic tests;
- time interval between system diagnostic tests;
m - number of protective switching devices;
n – Number of units of electrical equipment.
The formula holds if the condition is satisfied:  .
.
Conclusions
This master's work is carried out with the aim of assessing the level of vitality of the 0.4kV loading node, (TP, RU), feeding the end-user. Also, the influence of the parameters of the selected electrical equipment on the intensity of the appearance of a chain failure in the power supply system caused by the short circuit will be considered.
When writing this essay the master's work is not completed yet, the deadline is June 2018. The submitted abstract is of a survey nature, further work will be directed at calculations and refinement of the obtained results.
List of sources
1. Kozlov B.A. Directory for calculating the reliability of the equipment of radio electronics and automatics / B.A. Kozlov, I.S. Ushakov - Moscow: Soviet Radio, 1975 - 472 pp.
2. Kovalev AP Method of calculation of reliability of complex electric power systems with allowance for element restoration / AP Kovalev, L.I. Serdyuk - Electricity, 1985 - No. 10 - 52-53 p.
3. Kovalev AP Application of logic-probabilistic methods for assessing the reliability of structurally-complex schemes / AP Kovalev, AV Spivakovsky - Electricity, 2000 - No. 9 - 66-70 p.
4. Reliability and efficiency in the technique: Reference book t.5: design reliability analysis / Ed. YOU. Ïîòóøåâà and Ë.È. Rebecca - M .: Mashinostroenie, 1988 - 316 p.
5. Ryabinin IA Fundamentals of the theory and calculation of reliability of ship electric power systems / IA Ryabinin - 2nd ed. - L .: Shipbuilding, 1971 - 456s.
6. Ryabinin IA Reliability and security of structurally complex systems. St. Petersburg.: Publishing house St. Petersburg, no., 2007. 276s.
7. Kulik B.A. Logic-probabilistic methods and algebra of tuples. - In: Theory and information technology of modeling the safety of complex systems, - St. Petersburg: IPMASHRAN, Prepring 123, no. 1995, issue 5.
