Реферат за темою випускної роботи
Зміст
- Вступ
- 1. Актуальність теми
- 2. Розробка математичної моделі для оцінки живучості вузлів навантаження 0,4/ 0,22 кВ
- 2.1 Постановка завдання в математичній формі.
- 2.2 Застосування теорії однорідних Марковських процесів для вирішення завдання.
- 2.3 Визначення середнього часу до втрати живучості вузла навантаження і дисперсії цього часу.
- Висновки
- Список джерел
Вступ
Поняття живучості відомо в техніці давно і практично використовується при створенні технічних систем різного призначення. До сих пір не створено єдиної теорії, яка об'єднувала б основні положення і поняття теорії живучості об'єкту, що не дозволяє розробляти на етапі проектування практичні рекомендації щодо забезпечення живучості складних систем.
При цьому проблема живучості продовжує залишатися однією з основних для сучасної техніки. Це пояснюється тим, що безперервно ускладнюються змогу оцінити потреби і одночасно підвищуються вимоги до надійності їх виконання.
В останні роки спостерігається значне підвищення інтересу до цієї характеристики, як в теоретичному, так і в практичному відношенні, в зв'язку зі зростанням збитків від тривалого відключення навіть частини системи, і збільшенням частки технологічно пов'язаних порушень працездатності, а, отже, масштабів «поразки» системи .
1. Актуальність теми
Ускладнення систем йде в різних галузях промисловості. З одного боку, до складу технічних систем входить все більше число комплектуючих елементів, з іншого боку, ускладнюється їх структура, що визначає з'єднання окремих елементів і їх взаємодію в процесі функціонування і підтримки працездатності.
Система, що складається з великого числа комплектуючих елементів і має складну структуру функціонування, вимагає розробки спеціальних методів забезпечення, підвищення і підтримки живучості таких систем, включаючи розробку математичних методів.
Прагнення до зменшення розмірів пошкоджуваності системи одночасно є прагненням до створення більш сприятливих умови для відновлення належного рівня функціонування. Крім того, внаслідок розвинених зв'язків між різними системами і підсистемами по різних каналах (інформаційні, матеріальні, енергетичні) значну роль можуть грати вторинні наслідки порушень працездатності елементів системи. Збиток від вторинних ушкоджень може бути не менше, ніж від первинних, аж до припинення функціонування системи.
У зв'язку з цим необхідно систематизувати основні методи і підходи до оцінки живучості систем електропостачання, зокрема, для вузлів навантаження, що живлять кінцевого споживача.
2. Мета і завдання дослідження, плановані результати
2.1 Постановка завдання в математичній формі.
В електриці під живучістю об'єкту розуміється властивість протистояти збурень, не допускаючи їх каскадного розвитку з масовим порушенням живлення споживачів [ 1 ]. Живучістю вузла навантаження будемо вважати здатність споживачів і їх автоматичних засобів в захисту протистояти збурень, які можуть привести до аварійного його відключення. Живучість вузла навантаження залежить від структури системи електропостачання та її конфігурації, надійності електроустаткування, засобів РЗ і протиаварійної автоматики, а також від кваліфікації обслуговуючого його персоналу, запасу стійкості, резерву активної потужності.
При КЗ в елементах мережі та відмову в спрацьовуванні ряду захисних комутаційних апаратів, через які протікав наскрізної аварійний струм, відбуваються так звані ланцюгові аварії. На їх частку припадає 90% збитку, що наноситься споживачам електричної енергії. Ступінь розлади функціонування установок при аваріях і порушеннях в роботі називають глибиною. Глибина цепочечной аварії залежить від місця появи КЗ і числа відключилися комутаційних апаратів, через які протікав наскрізної аварійний струм і привів в дію їх струмові захисту. Глибину цепочечной аварії можна характеризувати числом помилково відключилися непошкоджених споживачів (секції шин) або їх збитками, які пов'язані з Недовідпуск електроенергії, простоєм устаткування і розладами технологічних циклів.
Захисні пристрої (автоматичний вимикач, УЗО) належать до класу чергових систем, що мають два режими роботи: режим тривоги, що триває частки секунди або кілька секунд, і режим чергування (очікування) - сотні годин. У першому режимі пристрій повинен спрацьовувати, у другому - бути готовим до спрацьовування, але не спрацьовувати [ 2 ].
Слід розрізняти два види відмов захисних пристроїв: неспрацювання пристрою при наявності на вході відповідного впливу (відмова спрацювання) і спрацьовування пристрою при відсутності впливу (помилкові, зайві спрацьовування). [3].
Наслідки порушення надійності по селективності і безвідмовності захисного комутаційного апарату різні. Помилкове спрацьовування захисного комутаційного апарату призводить до знеструмлення споживачів приміщень на час повторного (вручну або автоматичного) включення апарату захисту.
Случайно інтервал часу між суміжними КЗ в зоні дії захисного комутаційного апарату позначимо через ![]() , а час існування КЗ (час спрацьовування захисту будемо розглядати як випадкову величину) через
, а час існування КЗ (час спрацьовування захисту будемо розглядати як випадкову величину) через ![]() .
.
позначимо через ![]() випадковий інтервал часу між відмовами захисного комутаційного апарату. Випадкове час знаходження захисного комутаційного апарату в невиявлення відмовив стані позначимо через
випадковий інтервал часу між відмовами захисного комутаційного апарату. Випадкове час знаходження захисного комутаційного апарату в невиявлення відмовив стані позначимо через ![]() Випадкова величина
Випадкова величина ![]() залежить від надійності елементів захисного пристрою, періодичного контролю його працездатності і кваліфікації обслуговуючого персоналу.
залежить від надійності елементів захисного пристрою, періодичного контролю його працездатності і кваліфікації обслуговуючого персоналу.
При випадковому збігу незалежних випадкових інтервалів часу ![]() та
та ![]() происходит потеря живучести узлов нагрузки 0,4кВ, причиной которого является КЗ.
происходит потеря живучести узлов нагрузки 0,4кВ, причиной которого является КЗ.
Зміна стану мережі, що захищається в часі представимо у вигляді випадкової функції n (t), яка може приймати два значення: «0» і «1». Стан «0» - в мережі, що захищається немає пошкоджень, що призводять до КЗ. Стан «1» - в мережі, що захищається відбулося КЗ.
Послідовність чергуються інтервалів часу між КЗ позначимо через ![]() , а тривалість існування КЗ (тривалість спрацьовування захисного комутаційного апарату) - через
, а тривалість існування КЗ (тривалість спрацьовування захисного комутаційного апарату) - через ![]() .
.
Всі величини ![]() мають розподіл:
мають розподіл: ![]() ; а всі
; а всі ![]() - расподіл
- расподіл ![]() .
.
Всі величини ![]() мають розподіл:
мають розподіл: ![]() ; а всі
; а всі ![]() - расподіл
- расподіл ![]() .
.
Величина  - середній інтервал часу між появами КЗ в мережі, що захищається;
- середній інтервал часу між появами КЗ в мережі, що захищається;  -середній час існування струму КЗ (або середній час спрацьовування захисного комутаційного апарату).
-середній час існування струму КЗ (або середній час спрацьовування захисного комутаційного апарату).
Величини ![]() и
и ![]() взаємно незалежні. Переходи зі стану «0»> «1» і «1»> «0» відбуваються миттєво без витримки часу.
взаємно незалежні. Переходи зі стану «0»> «1» і «1»> «0» відбуваються миттєво без витримки часу.
Стан захисного комутаційного апарату опишемо аналогічною функцією Е (t), яка може приймати два значення: «0» і «1». Стан «0» означає, що захисний комутаційний апарат знаходиться в працездатному стані, а «1» - в схемі максимального струмового захисту є пошкодження. Послідовність чергуються випадкових інтервалів часу ![]() відображає працездатний стан схеми, а послідовність
відображає працездатний стан схеми, а послідовність ![]() - неработоспособное.
- неработоспособное.
Нехай все ![]() мають один і той же розподіл
мають один і той же розподіл ![]() а всі
а всі ![]() - расподіл
- расподіл ![]() .
.
Величини  - середній інтервал часу між відмовами в спрацьовуванні захисного комутаційного апарату;
- середній інтервал часу між відмовами в спрацьовуванні захисного комутаційного апарату;  - середній час перебування захисного комутаційного апарату в невиявлення відмовив стані.
- середній час перебування захисного комутаційного апарату в невиявлення відмовив стані.
Величини ![]() та
та ![]() взаємно незалежні. Переходи зі стану «0»> «1» і «1»> «0» відбуваються миттєво без витримки часу.
взаємно незалежні. Переходи зі стану «0»> «1» і «1»> «0» відбуваються миттєво без витримки часу.
Експоненціальна модель розподілу інтервалів часу ![]() и
и ![]() погано підтверджується на практиці, однак, аналогічно тому, як це зроблено в роботах [4], якщо інтервали часу між відмовами
погано підтверджується на практиці, однак, аналогічно тому, як це зроблено в роботах [4], якщо інтервали часу між відмовами ![]() и
и ![]() мають експонентний закон розподілу і функції розподілу ймовірностей випадкових величин
мають експонентний закон розподілу і функції розподілу ймовірностей випадкових величин ![]() и
и ![]() мають такі властивості:
мають такі властивості:
1. Випадкові величини мають не нульове математичної:
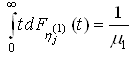 ;
;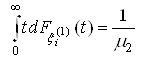 ;
;2. Випадкові величини мають кінцевий другий момент:
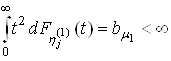 ;
;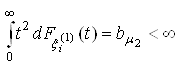 ;
;3. клас функцій ![]() и
и ![]() виходить з однієї функції за допомогою зміни масштабу по осі абсцис:
виходить з однієї функції за допомогою зміни масштабу по осі абсцис:
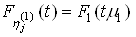 ;
;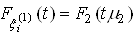 ;
;Те інтенсивність втрати живучості взагалі не залежить від функцій розподілу ймовірностей випадкових величин ![]() и
и ![]() , а визначається тільки середніми значеннями d1 і d2.[6].
, а визначається тільки середніми значеннями d1 і d2.[6].
Втрата живучості вузла навантаження 0,4 кВ настає в момент зустрічі процесів ![]() в стані 1, т. е. коли захисний комутаційний апарат (через його відмови) не може відключити випадково з'явився в захищається зоні струм КЗ (рис.1).
в стані 1, т. е. коли захисний комутаційний апарат (через його відмови) не може відключити випадково з'явився в захищається зоні струм КЗ (рис.1).
Завдання полягає в тому, щоб знаючи параметри процесів ![]() визначити: середній час до втрати живучості вузла навантаження 0,4 кВ
визначити: середній час до втрати живучості вузла навантаження 0,4 кВ ![]() дисперсію цього часу
дисперсію цього часу ![]() , ймовірність знаходження системи в кожному з можливих станів
, ймовірність знаходження системи в кожному з можливих станів ![]() , ймовірність втрати живучості вузла навантаження 0,4 кВ. Q (t).
, ймовірність втрати живучості вузла навантаження 0,4 кВ. Q (t).
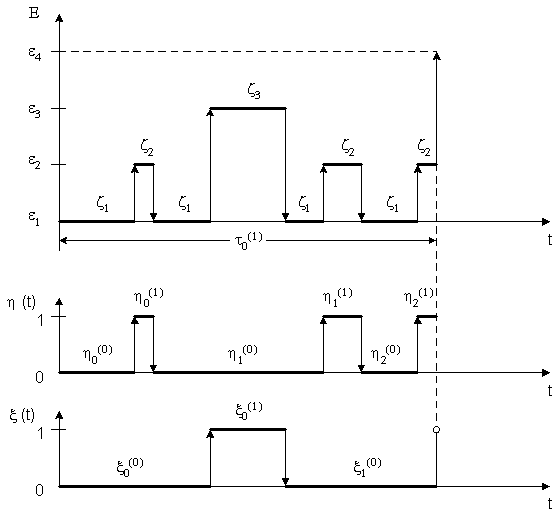
Малюнок 1 - Можлива реалізація Марківського випадкового процесу з дискретними станами і безперервним часом:
![]() - стан системи;
- стан системи;
![]() - випадкові процеси;
- випадкові процеси;
![]() ,
, ![]() - час знаходження захищається в безпечному стані і середній час спрацьовування захисного комутаційного апарату відповідно;
- час знаходження захищається в безпечному стані і середній час спрацьовування захисного комутаційного апарату відповідно;
![]() ,
, ![]() - час знаходження захисного комутаційного апарату в безвідмовному і відмовив станах відповідно.
- час знаходження захисного комутаційного апарату в безвідмовному і відмовив станах відповідно.
2.2 Застосування теорії однорідних марковських процесів для вирішення завдання.
Про статистичної природі випадкових функцій ![]() припустимо наступне. Імовірність переходів для функції
припустимо наступне. Імовірність переходів для функції ![]() з безпечного стану в небезпечне за проміжок часу
з безпечного стану в небезпечне за проміжок часу ![]() дорівнює
дорівнює ![]() , а переходів з небезпечного стану в безпечне -
, а переходів з небезпечного стану в безпечне - ![]() , де
, де ![]() означає, що поява в інтервалі часу
означає, що поява в інтервалі часу ![]() більше одного небезпечного (безпечного) стану є нескінченно малою величиною вищого порядку ніж інші величини. Величини
більше одного небезпечного (безпечного) стану є нескінченно малою величиною вищого порядку ніж інші величини. Величини ![]() и
и ![]() є параметрами процесу
є параметрами процесу ![]() . Параметр
. Параметр ![]() характеризує частоту або швидкість, з якою безпечні стану змінюються на небезпечні, а
характеризує частоту або швидкість, з якою безпечні стану змінюються на небезпечні, а ![]() характерізует частоту або швидкість, з якою небезпечні стану змінюються на безпечні.
характерізует частоту або швидкість, з якою небезпечні стану змінюються на безпечні.
для функції![]() ймовірність переходу з безпечного стану в небезпечне за час
ймовірність переходу з безпечного стану в небезпечне за час ![]() дорівнює
дорівнює ![]() ,а зворотний перехід здійснюється з імовірністю
,а зворотний перехід здійснюється з імовірністю ![]() .
.
Параметр ![]() характерізует швидкість зміни безпечних проміжків часу на небезпечні, а
характерізует швидкість зміни безпечних проміжків часу на небезпечні, а ![]() -швидкість зміни небезпечних проміжків часу на безпечні. Прийняті допущення означають, що
-швидкість зміни небезпечних проміжків часу на безпечні. Прийняті допущення означають, що ![]() можна розглядати як два Марковських процесу з двома станами: «0» - безпечне, «1» - небезпечне.
можна розглядати як два Марковських процесу з двома станами: «0» - безпечне, «1» - небезпечне.
Втрата живучості в цьому описі настає в момент зустрічі процесів ![]() в состоянии 1, т. е. когда
в состоянии 1, т. е. когда ![]() .
.
Будемо вважати, що в початковий момент часу ![]() , т. е. захисний комутаційний апарат справний і знаходиться в режимі очікування; КЗ в мережі, що захищається відсутня.
, т. е. захисний комутаційний апарат справний і знаходиться в режимі очікування; КЗ в мережі, що захищається відсутня.
сукупність процесів ![]() розглянемо як один Марковський процес
розглянемо як один Марковський процес ![]() з 4 дискретними станами і безперервним часом. Система в будь-який момент часу t може знаходиться в одному з кінцевого безлічі станів:
з 4 дискретними станами і безперервним часом. Система в будь-який момент часу t може знаходиться в одному з кінцевого безлічі станів:
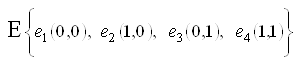 ,
,Де, ![]() - в мережі, що захищається відсутня КЗ, захисний комутаційний апарат справний і знаходиться в «режимі» режимі;
- в мережі, що захищається відсутня КЗ, захисний комутаційний апарат справний і знаходиться в «режимі» режимі;
![]() - в мережі, що захищається відбулося КЗ, захисний комутаційний апарат справний і готовий відключити струм КЗ;
- в мережі, що захищається відбулося КЗ, захисний комутаційний апарат справний і готовий відключити струм КЗ;
![]() - в мережі, що захищається КЗ відсутній, захисний комутаційний апарат знаходиться в відмовив стані;
- в мережі, що захищається КЗ відсутній, захисний комутаційний апарат знаходиться в відмовив стані;
![]() - в мережі, що захищається відбулося КЗ, захисний комутаційний апарат знаходиться в відмовив стані.
- в мережі, що захищається відбулося КЗ, захисний комутаційний апарат знаходиться в відмовив стані.
При випадковому попаданні системи в стан ![]() вузол навантаження 0,4 кВ втрачає живучість.
вузол навантаження 0,4 кВ втрачає живучість.
Позначимо через ![]() ймовірність того, що система за малий проміжок часу
ймовірність того, що система за малий проміжок часу ![]() залишиться в стані
залишиться в стані ![]() ,
, ![]() и через
и через ![]() - ймовірність того, що система за час
- ймовірність того, що система за час ![]() перейде зі стану
перейде зі стану ![]() у стан
у стан ![]() ,
, ![]() ,
, ![]() . Ці ймовірності переходів визначаються таким чином:
. Ці ймовірності переходів визначаються таким чином:
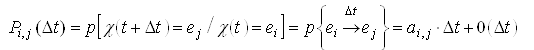 ; (1)
; (1)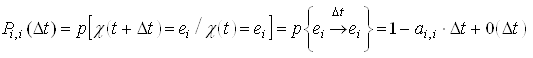 . (2)
. (2)У формулі (1) величина ![]() враховує з точністю до членів другого порядку малості, що за час
враховує з точністю до членів другого порядку малості, що за час ![]() відбудеться перехід системи зі стану
відбудеться перехід системи зі стану ![]() в інший стан
в інший стан ![]() , а у формулі (2) величина
, а у формулі (2) величина ![]() враховує з точністю до членів другого порядку малості, що за час
враховує з точністю до членів другого порядку малості, що за час ![]() не відбудеться перехід системи зі стану
не відбудеться перехід системи зі стану ![]() в будь-який інший стан, т. е. процес залишиться в стані
в будь-який інший стан, т. е. процес залишиться в стані ![]() .
.
позначимо через ![]() ,
, ![]() час перебування процесу в стані
час перебування процесу в стані ![]() . Для регулярного однорідного Марківського процесу розподіл випадкових величин
. Для регулярного однорідного Марківського процесу розподіл випадкових величин ![]() який суперечить експоненційної функції розподілу ймовірностей [5]:
який суперечить експоненційної функції розподілу ймовірностей [5]:
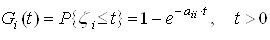 . (3)
. (3)Регулярний однорідний Марковський процес з дискретними станами і безперервним часом ![]() буде Повністю визначення, если буде відомо Розподіл (3) і матриця ймовірностей переходів
буде Повністю визначення, если буде відомо Розподіл (3) і матриця ймовірностей переходів ![]() :
:
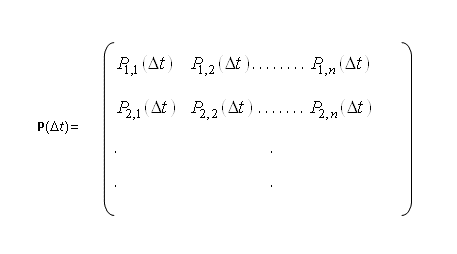 . (4)
. (4)Матриця (4) є квадратної з невід'ємними елементами, причому сума елементів в кожному рядку дорівнює 1. [7].
Використовуючи формули (1) і (2) визначимо ймовірність знаходження системи час ![]() у стаі «0»
у стаі «0» ![]() , ймовірність переходу за час
, ймовірність переходу за час![]() зі стану «1» в «0»
зі стану «1» в «0» ![]() , ймовірність знаходження системи час
, ймовірність знаходження системи час ![]() у стані «1»
у стані «1» ![]() , ймовірність переходу за час
, ймовірність переходу за час ![]() зі стану «0» в стан «1»
зі стану «0» в стан «1» ![]() :
:
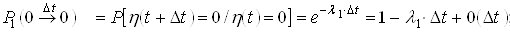 ;
;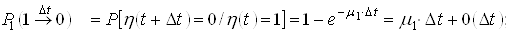 ;
;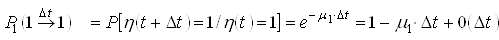 ;
;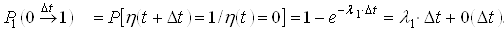 .
.Захисний комутаційний апарат також може знаходитися в двох станах: «0» - безпечний стан, захисний комутаційний апарат знаходиться в «режимі» режимі; стан «1» - захисний комутаційний апарат знаходиться в небезпечному (відмовив) стані.
Вікорістовуючі формули (1) і (2) знаходімо ймовірності переходів для захисних комутаційного апарату за годину ![]() :
:
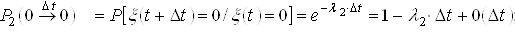 ;
;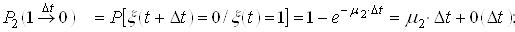 ;
;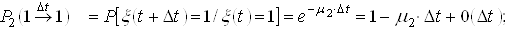 ;
;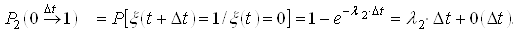 .
.Визначимо ймовірності переходів для системи, описується сукупністю двох випадкових функцій ![]() :
:
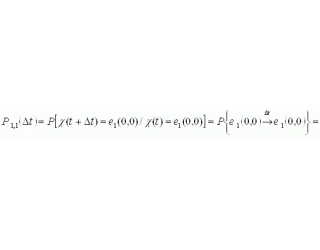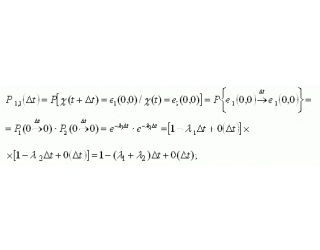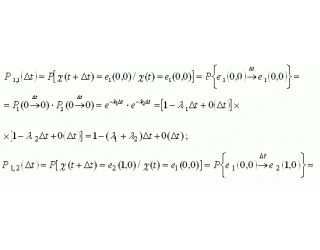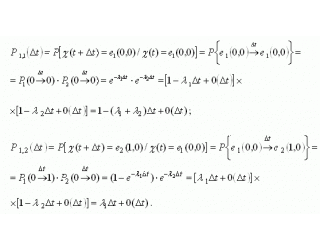
где ![]() означає, що два переходи за час
означає, що два переходи за час ![]() є величина нескінченно мала:
є величина нескінченно мала:
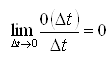 .
.2.3 Визначення середнього часу до втрати живучості вузла навантаження і дисперсії цього часу.
Ймовірності перебування системи в кожному з можливих безвідмовних станах визначаються з системи лінійних диференціальних рівнянь:
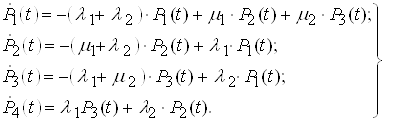 .(5)
.(5)Система (5) вирішується за початкових умов  .
.
Імовірність втрати живучості вузлом навантаження 0,4 кВ знаходиться наступним чином:
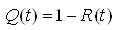 ,
,Де  ,
,
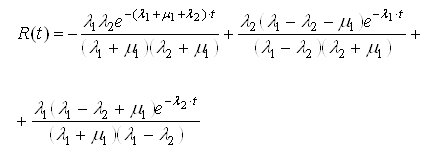 .
.Імовірність втрати живучості вузла навантаження протягом часу t:
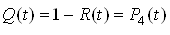 .
.Середній час ![]() до втрати живучості вузла навантаження пожежі можна визначити за формулою:
до втрати живучості вузла навантаження пожежі можна визначити за формулою:
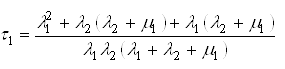 .
.дисперсію часу ![]() можна визначити, користуючись виразом:
можна визначити, користуючись виразом:
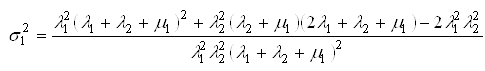 .
.У тому випадку, якщо виконується умова ![]() , то:
, то:
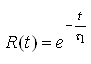 .
.Показником живучості може служити частота появи системних ланцюгових аварій з різною глибиною порушення електропостачання:
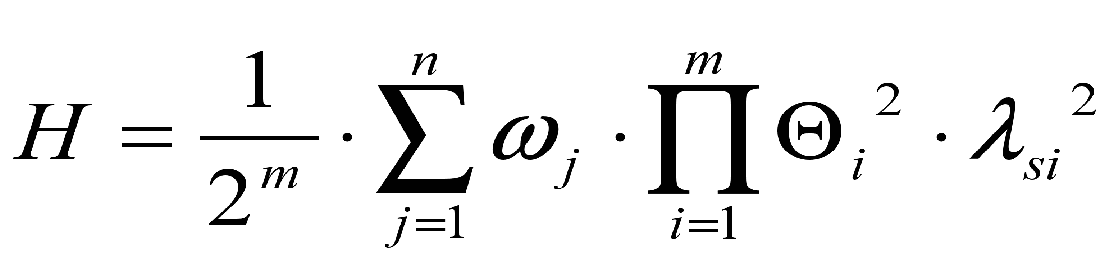 .
.Де ![]() - параметр потоку незалежних КЗ в j-тому елементі мережі;
- параметр потоку незалежних КЗ в j-тому елементі мережі;
![]() - параметр потоку відмов в спрацьовуванні захисного комутаційного апарату;
- параметр потоку відмов в спрацьовуванні захисного комутаційного апарату;
![]() - інтервал часу між діагностичними перевірками системи;
- інтервал часу між діагностичними перевірками системи;
m - число захисних комутаційних апаратів; число захисних комутаційних апаратів;
n – число одиниць електрообладнання.
Формула справедлива при виконанні умови:  .
.
Висновки
Дана магістерська робота виконується з метою оцінки рівня живучості вузла навантаження 0,4 кВ, (ТП, РП), яке живить кінцевого споживача. Також буде розглянуто вплив параметрів обраного електрообладнання на інтенсивність появи цепочечной аварії в системі електропостачання, викликаного КЗ.
При написанні даного реферату магістерська робота ще не завершена, термін завершення - червень 2018 р. Представлений реферат носить оглядовий характер, подальша робота буде спрямована на розрахунки і доопрацювання отриманих результатів.
Список джерел
1. Козлов Б.А. Довідник з розрахунку надійності апаратури радіоелектроніки та автоматики / Б.А. Козлов, І.С. Ушаков - М .: Радянське радіо, 1975 - 472 с.
2. Ковальов О.П. Метод розрахунку надійності складних систем електропостачання з урахуванням відновлення елементів / А.П. Ковальов, Л.І. Сердюк - Електрика, 1985 - №10 - 52-53 с.
3. Ковальов О.П. Застосування логіко-імовірнісних методів для оцінки надійності структурно-складних схем / А.П. Ковальов, А.В. Співаковський - Електрика, 2000 - №9 - 66-70 с.
4. Надійність і ефективність в техніці: Довідник т.5: проектний аналіз надійності / Под ред. В.І. Потушева і Л.І. Рембези. - М .: Машинобудування, 1988 - 316 с.
5. Рябінін І.А. Основи теорії і розрахунку надійності суднових електроенергетичних систем / І.А. Рябінін - 2-е вид. - Л .: Суднобудування, 1971. - 456с.
6. Рябінін І.А. Надійність і безпека структурно складних систем. СПБ.: Изд-во С.-Петербург ун-ту, 2007.- 276с.
7. Кулик Б.А. Логіко-імовірнісні методи і алгебра кортежів. - В сб .: Теорія таінформаційний техніка моделювання безпеки складних систем, - Санкт-Петербург: ІПМАШРАН, Препрінг 123, вип. 1995 року, вип 5.
