Реферат по теме выпускной работы
Содержание
- Введение
- 1. Актуальность темы
- 2. Разработка математической модели для оценки живучести узлов нагрузки 0,4/0,22 кВ
- 2.1 Постановка задачи в математической форме.
- 2.2 Применение теории однородных Марковских процессов для решения задачи.
- 2.3 Определение среднего времени до потери живучести узла нагрузки и дисперсии этого времени.
- Выводы
- Список источников
Введение
Понятие живучести известно в технике давно и практически используется при создании технических систем различного назначения. До сих пор не создано единой теории, которая объединяла бы основные положения и понятия теории живучести объекта, что не позволяет разрабатывать на этапе проектирования практические рекомендации по обеспечению живучести сложных систем.
При этом проблема живучести продолжает оставаться одной из основных для современной техники. Это объясняется тем, что непрерывно усложняются решаемые задачи и одновременно повышаются требования к надежности их выполнения.
В последние годы наблюдается значительное повышение интереса к этой характеристике, как в теоретическом, так и в практическом отношении, в связи с возрастанием ущерба от длительного отключения даже части системы, и увеличением доли технологически связанных нарушений работоспособности, а, следовательно, масштабов «поражения» системы.
1. Актуальность темы
Усложнение систем идет в различных отраслях промышленности. С одной стороны, в состав технических систем входит все большее число комплектующих элементов, с другой стороны, усложняется их структура, определяющая соединение отдельных элементов и их взаимодействие в процессе функционирования и поддержания работоспособности.
Система, состоящая из большого числа комплектующих элементов и имеющая сложную структуру функционирования, требует разработки специальных методов обеспечения, повышения и поддержания живучести таких систем, включая разработку математических методов.
Стремление к уменьшению размеров повреждаемости системы одновременно является стремлением к созданию более благоприятных условия для восстановления требуемого уровня функционирования. Кроме того, вследствие развитых связей между различными системами и подсистемами по различным каналам (информационные, материальные, энергетические) значительную роль могут играть вторичные последствия нарушений работоспособности элементов системы. Ущерб от вторичных повреждений может быть не меньше, чем от первичных, вплоть до прекращения функционирования системы.
В связи с этим необходимо систематизировать основные методы и подходы к оценке живучести систем электроснабжения, в частности, для узлов нагрузки, питающих конечного потребителя.
2. Цель и задачи исследования, планируемые результаты
2.1 Постановка задачи в математической форме.
В электрике под живучестью объекта понимается свойство противостоять возмущениям, не допуская их каскадного развития с массовым нарушением питания потребителей [1]. Живучестью узла нагрузки будем считать способность потребителей и их автоматических средств в защиты противостоять возмущениям, которые могут привести к аварийному его отключению. Живучесть узла нагрузки зависит от структуры системы электроснабжения и ее конфигурации, надежности электрооборудования, средств РЗ и противоаварийной автоматики, а также от квалификации обслуживающего его персонала, запаса устойчивости, резерва активной мощности.
При КЗ в элементах сети и отказе в срабатывании ряда защитных коммутационных аппаратов, через которые протекал сквозной аварийный ток, происходят так называемые цепочечные аварии. На их долю приходится 90 % ущерба, наносимого потребителям электрической энергии. Степень расстройства функционирования установок при авариях и нарушениях в работе называют глубиной. Глубина цепочечной аварии зависит от места появления КЗ и числа отключившихся коммутационных аппаратов, через которые протекал сквозной аварийный ток и привел в действие их токовые защиты. Глубину цепочечной аварии можно характеризовать числом ложно отключившихся неповрежденных потребителей (секции шин) либо их убытками, которые связаны с недоотпуском электроэнергии, простоем оборудования и расстройствами технологических циклов.
Защитные устройства (автоматический выключатель, УЗО) принадлежат к классу дежурных систем, имеющих два режима работы: режим тревоги, длящийся доли секунды или несколько секунд, и режим дежурства (ожидания) – сотни часов. В первом режиме устройство должно срабатывать, во втором – быть готовым к срабатыванию, но не срабатывать [2].
Следует различать два вида отказов защитных устройств: несрабатывание устройства при наличии на входе соответствующего воздействия (отказ срабатывания) и срабатывание устройства при отсутствии воздействия (ложные, излишние срабатывания). [3].
Последствия нарушения надежности по селективности и безотказности защитного коммутационного аппарата различны. Ложное срабатывание защитного коммутационного аппарата приводит к обесточиванию потребителей помещений на время повторного (вручную или автоматического) включения аппарата защиты.
Случайный интервал времени между смежными КЗ в зоне действия защитного коммутационного аппарата обозначим через ![]() , а время существования КЗ (время срабатывания защиты будем рассматривать как случайную величину) через
, а время существования КЗ (время срабатывания защиты будем рассматривать как случайную величину) через ![]() .
.
Обозначим через ![]() случайный интервал времени между отказами защитного коммутационного аппарата. Случайное время нахождения защитного коммутационного аппарата в необнаруженном отказавшем состоянии обозначим через
случайный интервал времени между отказами защитного коммутационного аппарата. Случайное время нахождения защитного коммутационного аппарата в необнаруженном отказавшем состоянии обозначим через ![]() Случайная величина
Случайная величина ![]() зависит от надежности элементов защитного устройства, периодического контроля его работоспособности и квалификации обслуживающего персонала.
зависит от надежности элементов защитного устройства, периодического контроля его работоспособности и квалификации обслуживающего персонала.
При случайном совпадении независимых случайных интервалов времени ![]() и
и ![]() происходит потеря живучести узлов нагрузки 0,4кВ, причиной которого является КЗ.
происходит потеря живучести узлов нагрузки 0,4кВ, причиной которого является КЗ.
Изменение состояния защищаемой сети во времени представим в виде случайной функции n(t), которая может принимать два значения: «0» и «1». Состояние «0» – в защищаемой сети нет повреждений, приводящих к КЗ. Состояние «1» – в защищаемой сети произошло КЗ.
Последовательность чередующихся интервалов времени между КЗ обозначим через ![]() , а длительность существования КЗ (длительность срабатывания защитного коммутационного аппарата) – через
, а длительность существования КЗ (длительность срабатывания защитного коммутационного аппарата) – через ![]() .
.
Все величины ![]() имеют распределение:
имеют распределение: ![]() ; а все
; а все ![]() - распределение
- распределение ![]() .
.
Величина  - средний интервал времени между появлениями КЗ в защищаемой сети;
- средний интервал времени между появлениями КЗ в защищаемой сети;  - среднее время существования тока КЗ (или среднее время срабатывания защитного коммутационного аппарата).
- среднее время существования тока КЗ (или среднее время срабатывания защитного коммутационного аппарата).
Величины ![]() и
и ![]() взаимно независимы. Переходы из состояния «0» > «1» и «1» > «0» происходят мгновенно без выдержки времени.
взаимно независимы. Переходы из состояния «0» > «1» и «1» > «0» происходят мгновенно без выдержки времени.
Состояние защитного коммутационного аппарата опишем аналогичной функцией Е(t), которая может принимать два значения: «0» и «1». Состояние «0» означает, что защитный коммутационный аппарат находится в работоспособном состоянии, а «1» – в схеме максимальной токовой защиты есть повреждения. Последовательность чередующихся случайных интервалов времени ![]() отражает работоспособное состояние схемы, а последовательность
отражает работоспособное состояние схемы, а последовательность ![]() - неработоспособное.
- неработоспособное.
Пусть все ![]() имеют одно и то же распределение
имеют одно и то же распределение ![]() а все
а все ![]() - распределение
- распределение ![]() .
.
Величины  - средний интервал времени между отказами в срабатывании защитного коммутационного аппарата;
- средний интервал времени между отказами в срабатывании защитного коммутационного аппарата;  - среднее время нахождения защитного коммутационного аппарата в необнаруженном отказавшем состоянии.
- среднее время нахождения защитного коммутационного аппарата в необнаруженном отказавшем состоянии.
Величины ![]() и
и ![]() взаимно независимы. Переходы из состояния «0» > «1» и «1» > «0» происходят мгновенно без выдержки времени.
взаимно независимы. Переходы из состояния «0» > «1» и «1» > «0» происходят мгновенно без выдержки времени.
Экспоненциальная модель распределения интервалов времени ![]() и
и ![]() плохо подтверждается на практике, однако, аналогично тому, как это сделано в работах [4], если интервалы времени между отказами
плохо подтверждается на практике, однако, аналогично тому, как это сделано в работах [4], если интервалы времени между отказами ![]() и
и ![]() имеют экспоненциальный закон распределения и функции распределения вероятностей случайных величин
имеют экспоненциальный закон распределения и функции распределения вероятностей случайных величин ![]() и
и ![]() обладают следующими свойствами:
обладают следующими свойствами:
1. Случайные величины имеют не нулевое математической:
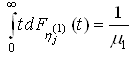 ;
;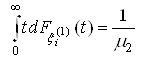 ;
;2. Случайные величины имеют конечный второй момент:
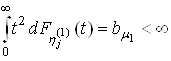 ;
;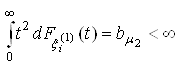 ;
;3. Класс функций ![]() и
и ![]() получается из одной функции посредством изменения масштаба по оси абсцисс:
получается из одной функции посредством изменения масштаба по оси абсцисс:
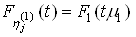 ;
;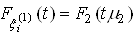 ;
;То интенсивность потери живучести вообще не зависит от функций распределения вероятностей случайных величин ![]() и
и ![]() , а определяется только средними значениями d1 и d2.[6].
, а определяется только средними значениями d1 и d2.[6].
Потеря живучести узла нагрузки 0,4кВ наступает в момент встречи процессов ![]() в состоянии 1, т. е. когда защитный коммутационный аппарат (из-за его отказа) не может отключить случайно появившийся в защищаемой зоне ток КЗ (рис.1).
в состоянии 1, т. е. когда защитный коммутационный аппарат (из-за его отказа) не может отключить случайно появившийся в защищаемой зоне ток КЗ (рис.1).
Задача состоит в том, чтобы зная параметры процессов ![]() определить: среднее время до потери живучести узла нагрузки 0,4кВ
определить: среднее время до потери живучести узла нагрузки 0,4кВ ![]() дисперсию этого времени
дисперсию этого времени ![]() , вероятность нахождения системы в каждом из возможных состояний
, вероятность нахождения системы в каждом из возможных состояний ![]() , вероятность потери живучести узла нагрузки 0,4кВ. Q(t).
, вероятность потери живучести узла нагрузки 0,4кВ. Q(t).
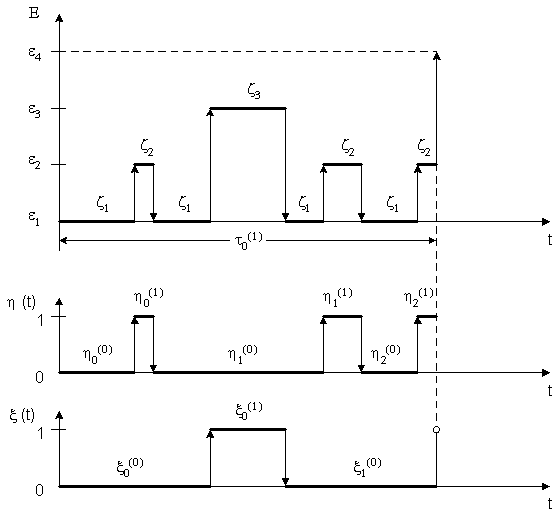
Рисунок 1 – Возможная реализация Марковского случайного процесса с дискретными состояниями и непрерывным временем:
![]() - состояния системы;
- состояния системы;
![]() - случайные процессы;
- случайные процессы;
![]() ,
, ![]() - время нахождения защищаемой сети в безопасном состоянии и среднее время срабатывания защитного коммутационного аппарата соответственно;
- время нахождения защищаемой сети в безопасном состоянии и среднее время срабатывания защитного коммутационного аппарата соответственно;
![]() ,
, ![]() - время нахождения защитного коммутационного аппарата в безотказном и отказавшем состояниях соответственно.
- время нахождения защитного коммутационного аппарата в безотказном и отказавшем состояниях соответственно.
2.2 Применение теории однородных марковских процессов для решения задачи.
О статистической природе случайных функций ![]() предположим следующее. Вероятность переходов для функции
предположим следующее. Вероятность переходов для функции ![]() из безопасного состояния в опасное за промежуток времени
из безопасного состояния в опасное за промежуток времени ![]() равна
равна ![]() , а переходов из опасного состояния в безопасное -
, а переходов из опасного состояния в безопасное - ![]() , где
, где ![]() означает, что появление в интервале времени
означает, что появление в интервале времени ![]() более одного опасного (безопасного) состояния является бесконечно малой величиной более высокого порядка чем остальные величины. Величины
более одного опасного (безопасного) состояния является бесконечно малой величиной более высокого порядка чем остальные величины. Величины ![]() и
и ![]() являются параметрами процесса
являются параметрами процесса ![]() . Параметр
. Параметр ![]() характеризует частоту или скорость , с которой безопасные состояния меняются на опасные, а
характеризует частоту или скорость , с которой безопасные состояния меняются на опасные, а ![]() характеризует частоту или скорость, с которой опасные состояния меняются на безопасные.
характеризует частоту или скорость, с которой опасные состояния меняются на безопасные.
Для функции ![]() вероятность перехода из безопасного состояния в опасное за время
вероятность перехода из безопасного состояния в опасное за время ![]() равна
равна ![]() , а обратный переход осуществляется с вероятностью
, а обратный переход осуществляется с вероятностью ![]() .
.
Параметр ![]() характеризует скорость смены безопасных промежутков времени на опасные, а
характеризует скорость смены безопасных промежутков времени на опасные, а ![]() - скорость смены опасных промежутков времени на безопасные. Принятые допущения означают, что
- скорость смены опасных промежутков времени на безопасные. Принятые допущения означают, что ![]() можно рассматривать как два Марковских процесса с двумя состояниями: «0» – безопасное, «1» – опасное.
можно рассматривать как два Марковских процесса с двумя состояниями: «0» – безопасное, «1» – опасное.
Потеря живучести в этом описании наступает в момент встречи процессов ![]() в состоянии 1, т. е. когда
в состоянии 1, т. е. когда ![]() .
.
Будем считать, что в начальный момент времени ![]() , т. е. защитный коммутационный аппарат исправен и находится в режиме ожидания; КЗ в защищаемой сети отсутствует.
, т. е. защитный коммутационный аппарат исправен и находится в режиме ожидания; КЗ в защищаемой сети отсутствует.
Совокупность процессов ![]() рассмотрим как один Марковский процесс
рассмотрим как один Марковский процесс ![]() с 4 дискретными состояниями и непрерывным временем. Система в любой момент времени t может находится в одном из конечного множества состояний:
с 4 дискретными состояниями и непрерывным временем. Система в любой момент времени t может находится в одном из конечного множества состояний:
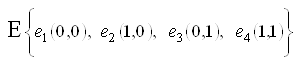 ,
,Где, ![]() - в защищаемой сети отсутствует КЗ, защитный коммутационный аппарат исправен и находится в «ждущем» режиме;
- в защищаемой сети отсутствует КЗ, защитный коммутационный аппарат исправен и находится в «ждущем» режиме;
![]() - в защищаемой сети произошло КЗ, защитный коммутационный аппарат исправен и готов отключить ток КЗ;
- в защищаемой сети произошло КЗ, защитный коммутационный аппарат исправен и готов отключить ток КЗ;
![]() - в защищаемой сети КЗ отсутствует, защитный коммутационный аппарат находится в отказавшем состоянии;
- в защищаемой сети КЗ отсутствует, защитный коммутационный аппарат находится в отказавшем состоянии;
![]() - в защищаемой сети произошло КЗ, защитный коммутационный аппарат находится в отказавшем состоянии.
- в защищаемой сети произошло КЗ, защитный коммутационный аппарат находится в отказавшем состоянии.
При случайном попадании системы в состояние ![]() узел нагрузки 0,4 кВ теряет живучесть.
узел нагрузки 0,4 кВ теряет живучесть.
Обозначим через ![]() вероятность того, что система за малый промежуток времени
вероятность того, что система за малый промежуток времени ![]() останется в состоянии
останется в состоянии ![]() ,
, ![]() и через
и через ![]() - вероятность того, что система за время
- вероятность того, что система за время ![]() перейдет из состояния
перейдет из состояния ![]() в состояние
в состояние ![]() ,
, ![]() ,
, ![]() . Эти вероятности переходов определяются следующим образом:
. Эти вероятности переходов определяются следующим образом:
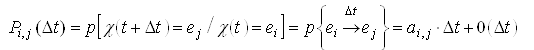 ; (1)
; (1)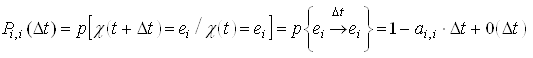 . (2)
. (2)В формуле (1) величина ![]() учитывает с точностью до членов второго порядка малости, что за время
учитывает с точностью до членов второго порядка малости, что за время ![]() произойдет переход системы из состояния
произойдет переход системы из состояния ![]() в другое состояние
в другое состояние ![]() , а в формуле (2) величина
, а в формуле (2) величина ![]() учитывает с точностью до членов второго порядка малости, что за время
учитывает с точностью до членов второго порядка малости, что за время ![]() не произойдет переход системы из состояния
не произойдет переход системы из состояния ![]() в любое другое состояние, т. е. процесс останется в состоянии
в любое другое состояние, т. е. процесс останется в состоянии ![]() .
.
Обозначим через ![]() ,
, ![]() время пребывания процесса в состоянии
время пребывания процесса в состоянии ![]() . Для регулярного однородного Марковского процесса распределение случайных величин
. Для регулярного однородного Марковского процесса распределение случайных величин ![]() не противоречит экспоненциальной функции распределения вероятностей [5]:
не противоречит экспоненциальной функции распределения вероятностей [5]:
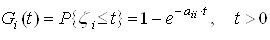 . (3)
. (3)Регулярный однородный Марковский процесс с дискретными состояниями и непрерывным временем ![]() будет полностью определен, если будет известно распределение (3) и матрица вероятностей переходов
будет полностью определен, если будет известно распределение (3) и матрица вероятностей переходов ![]() :
:
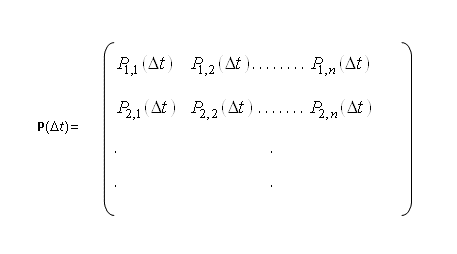 . (4)
. (4)Матрица (4) является квадратной с неотрицательными элементами, причем сумма элементов в каждой строке равна 1. [7].
Используя формулы (1) и (2) определим вероятность нахождения системы время ![]() в состоянии «0»
в состоянии «0» ![]() , вероятность перехода за время
, вероятность перехода за время ![]() из состояния «1» в «0»
из состояния «1» в «0» ![]() , вероятность нахождения системы время
, вероятность нахождения системы время ![]() в состоянии «1»
в состоянии «1» ![]() , вероятность перехода за время
, вероятность перехода за время ![]() из состояния «0» в состояние «1»
из состояния «0» в состояние «1» ![]() :
:
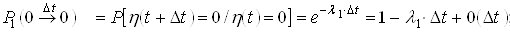 ;
;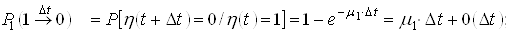 ;
;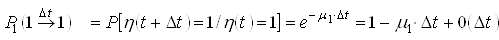 ;
;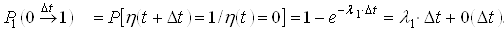 .
.Защитный коммутационный аппарат также может находиться в двух состояниях: «0» – безопасное состояние, защитный коммутационный аппарат находится в «ждущем» режиме; состояние «1» - защитный коммутационный аппарат находится в опасном (отказавшем) состоянии.
Используя формулы (1) и (2) находим вероятности переходов для защитного коммутационного аппарата за время ![]() :
:
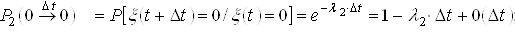 ;
;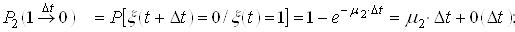 ;
;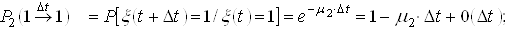 ;
;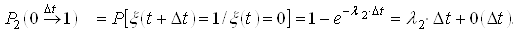 .
.Определим вероятности переходов для системы, описывающейся совокупностью двух случайных функций ![]() :
:
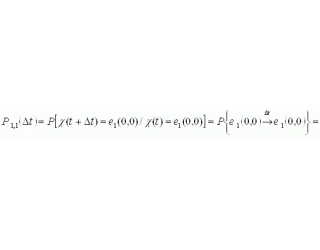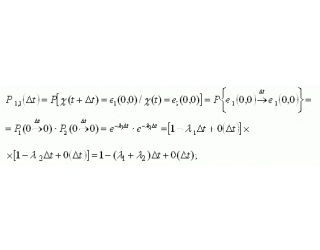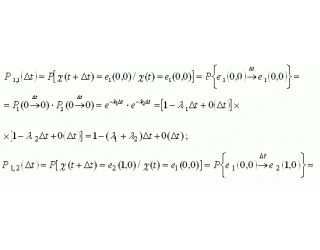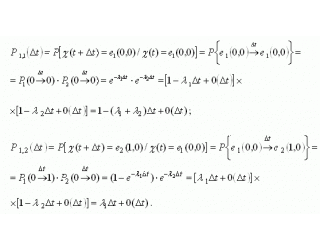
где ![]() означает, что два перехода за время
означает, что два перехода за время ![]() есть величина бесконечно малая:
есть величина бесконечно малая:
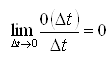 .
.2.3 Определение среднего времени до потери живучести узла нагрузки и дисперсии этого времени.
Вероятности пребывания системы в каждом из возможных безотказных состояниях определяются из системы линейных дифференциальных уравнений:
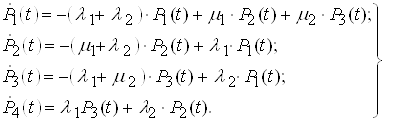 .(5)
.(5)Система (5) решается при начальных условиях  .
.
Вероятность потери живучести узлом нагрузки 0,4кВ находится следующим образом:
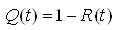 ,
,где  ,
,
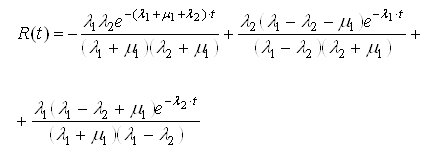 .
.Вероятность потери живучести узла нагрузки в течение времени t:
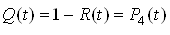 .
.Среднее время ![]() до потери живучести узла нагрузки пожара можно определить по формуле:
до потери живучести узла нагрузки пожара можно определить по формуле:
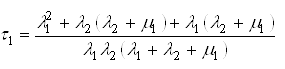 .
.Дисперсию времени ![]() можно определить, пользуясь выражением:
можно определить, пользуясь выражением:
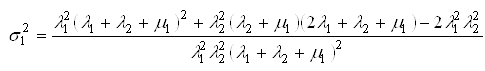 .
.В том случае, если выполняется условие ![]() , то:
, то:
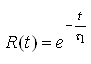 .
.Показателем живучести может служить частота появления системных цепочных аварий с различной глубиной нарушения электроснабжения:
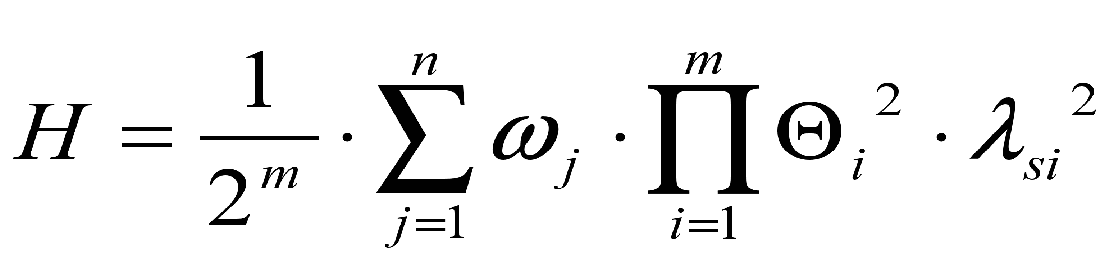 .
.где ![]() - параметр потока независимых КЗ в j-том элементе сети;
- параметр потока независимых КЗ в j-том элементе сети;
![]() - параметр потока отказов в срабатывании защитного коммутационного аппарата;
- параметр потока отказов в срабатывании защитного коммутационного аппарата;
![]() - интервал времени между диагностическими проверками системы;
- интервал времени между диагностическими проверками системы;
m - число защитных коммутационных аппаратов;
n – число единиц электрооборудования.
Формула справедлива при выполнении условия:  .
.
Выводы
Данная магистерская работа выполняется с целью оценки уровня живучести узла нагрузки 0,4кВ, (ТП, РУ), питающего конечного потребителя. Также будет рассмотрено влияние параметров выбираемого электрооборудования на интенсивность появления цепочечной аварии в системе электроснабжения, вызванного КЗ.
При написании данного реферата магистерская работа еще не завершена, срок завершения – июнь 2018г. Представленный реферат носит обзорный характер, дальнейшая работа будет направлена на расчеты и доработку полученных результатов.
Список источников
1. Козлов Б.А. Справочник по расчету надежности аппаратуры радиоэлектроники и автоматики / Б.А. Козлов, И.С. Ушаков – М.: Советское радио, 1975 – 472 с.
2. Ковалев А.П. Метод расчета надежности сложных систем электроснабжения с учетом восстановления элементов / А.П. Ковалев, Л.И. Сердюк – Электричество, 1985 – №10 – 52-53 с.
3. Ковалев А.П. Применение логико-вероятностных методов для оценки надежности структурно-сложных схем / А.П. Ковалев, А.В. Спиваковский – Электричество, 2000 – №9 – 66-70 с.
4. Надежность и эффективность в технике: Справочник т.5: проектный анализ надежности / Под ред. В.И. Потушева и Л.И. Рембезы. – М.: Машиностроение, 1988 – 316 с.
5. Рябинин И.А. Основы теории и расчета надежности судовых электроэнергетических систем / И.А. Рябинин – 2-е изд. – Л.: Судостроение, 1971. – 456с.
6. Рябинин И.А. Надежность и безопасность структурно сложных систем. СПБ.:Изд-во С.-Петербург ун-та, 2007.– 276с.
7. Кулик Б.А. Логико-вероятностные методы и алгебра кортежей. – В сб.: Теория иинформационная техника моделирования безопасности сложных систем, - Санкт-Петербург: ИПМАШРАН, Препринг 123, вып. 1995, вып 5.
