Abstract
Content
- Introduction
- 1. Relevance of theme
- 2. Analysis of research and publications
- 3. Results of the research
- Conclusion
- List of references
Introduction
A technique for assessing the reliability of structurally complex bridge circuits
is introduced, taking into account the two types of failures of protective equipment: open circuit failure
and failure to operate
.
Complex bridge circuits
are reduced to one equivalent element by converting a logical triangle
into an equally reliable star
and inversely converting a logical connection in the form of a star
to an equally reliable connection in the form of a triangle
.
Key words:reliability, system, complex structure, bridge circuit, triangle, star, probability of failures, type of failure, open circuit failure, failure to operate, probability of failure-free operation.
1. Relevance of theme
Systems unable to restore for certain reasons in the period under consideration will be referred to as systems unrestorable during the operation [1]. In this case, the system including at least one bridge circuit
will be referred to as a structurally complex circuit [2].
The methodology for assessing the reliability of unrestorable systems, the components of which can be found only in two incompatible states: operable and unoperable (open circuit failure
) has been developed to a sufficient extent [3 – 6].
To calculate the reliability of unrestorable systems, protective equipment is assumed to be absolutely reliable. In real systems of electricity, gas, water supply, etc., the protection means can work falsely (open circuit failure
), or fail to operate (failure to operate
).
Therefore, consideration of protective means reliability of structurally complex circuits is an urgent scientific and technical task, the solution of which will allow to significantly improve the accuracy of calculations and thereby predict the viability of the system under development at the design stage.
2. Analysis of research and publications
To evaluate the reliability of complex unrestorable systems whose elements can be in three incompatible states, there exist methods based on the use of decomposition of a complex structure into a base element, the use of the triangle-star
and star-triangle
method, as well as using n-tuple algebra [3 – 6].
Objective.Improvement of the methodology for assessing the reliability of power supply systems for industrial enterprises, taking into account the two types of electrical equipment failures.
3. Results of the research
Suppose all the components under consideration, of which the power supply system consists, fail independently, each component of the system can be in three incompatible states: operable, unoperable – open circuit failure
, unoperable – failure to operate
. Failure flows of components (open circuit failure
) and failure to operate
are the simplest;
the capacity of the components is unlimited, as well as the ability to restrain the flow of electricity, regardless of the number of short-circuited components, after the failure the component is not restored (not replaced by a new one) in the period under consideration [7].
Let Pi denote the probability of a failure-free operation of the i
system component, qoi – the probability of open circuit failure
in the i
component, and qsi – the probability of failure to operate
in the i
component. These three states constitute a complete group of incompatible events.
pi+qoi+qsi=1 (1)
The subscripts o
and s
in formula (1) indicate that component faults that lead to open circuit failures
or failures to operate
, respectively, are taken into account.
In case the two types of incompatible failures are observed in the components of the power supply system: open circuit failure
and failure to operate
, the probability of the i
component failure considering the two types of failures, during the time t can be determined using the formulas [8]:
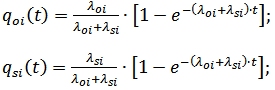
Formulas (2) and (3)
where
λoi, λsi – are constant failure rates of the i
component, considering its open circuit failure
and
failure to operate
respectively;
t – the current time of operation of the i
component of the system.
The circuit whose components can be connected in series, in parallel, in series-parallel or in parallel-series will be referred to as a structurally simple
circuit of the initial system substitution.
For a simple circuit of system substitution consisting of n
logical components connected in series, open circuit failure
or from i
components  leads to the disconnection between its
leads to the disconnection between its input
and output
.
If the probability of components failure of the substitution circuit qoi is given, the probability of disconnection between its input
and output
Qo is defined as follows:
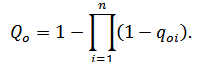
Formula (4)
In case each n
logical component connected in series fails to operate
in each of the i
elements, this will result in a steady leakage fault current flowing between the input
and output
of the substitution circuit.
If the probability of component failures of the substitution circuit qsi is given, the probability Qs of a steady leakage fault current flowing between the input
and the output
of the substitution circuit is defined using the formula:
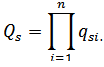
Formula (5)
For a simple circuit of system substitution consisting of m
logical components connected in parallel, open circuit failure
in each of the j
,  components leads to the disconnection between its
components leads to the disconnection between its input
and output
.
If the probability of components failure of the substitution circuit qoi is given, the probability Qo of the disconnection between its input
and output
is determined using the formula:
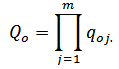
Formula (6)
In case any m
logical parallel connection of the components fails to operate
, this will result in a steady leakage fault current flowing between the input
and output
of the substitution circuit.
If the probability qsi,  of the components failure of the substitution circuit which consists of
of the components failure of the substitution circuit which consists of m
logical parallel connection of components is given, Qs – the probability of a steady leakage fault current flowing between the input
and the output
of the substitution circuit is defined using the formula:
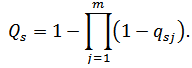
Formula (7)
To simplify the complicated
substitution circuit of the power supply system, the method of transitions from the logical triangle
to the equally reliable star
, or from the logical star
to the equally reliable logical triangle
(figure 1 a, b) should be used.

Fig. 1. Logical connection of the components in the form: a) triangle
; b) star
(animation: 7 frames, 8 cycles, 36 kilobytes)
Exact formulas of the transitions from the logical triangle
to the equally reliable star
(Fig. 1 a, b) and from the logical star
to the equally reliable logical triangle (Fig. 1 b, a) are given in [8,9].
Conclusion
1. A technique for assessing the reliability of structurally complex circuits of power supply systems, the elements of which can be in three incompatible states, is introduced.
2. The proposed technique
is useful for the case when: qoi≤0,1 and qsi≤0,1 where  .
.
List of references
1. Козлов Б.А. Справочник по расчету надежности аппаратуры радиоэлектроники и автоматики / Б.А. Козлов, И.С. Ушаков – М.: Советское радио, 1975 – 472 с.
2. Ковалев А.П. Метод расчета надежности сложных систем электроснабжения с учетом восстановления элементов / А.П. Ковалев, Л.И. Сердюк – Электричество, 1985 – №10 – С. 52-53.
3. Рябинин И.А. Основы теории и расчета надежности судовых электроэнергетических систем / И.А. Рябинин – 2-е изд. – Л.: Судостроение, 1971. – 456с.
4. Надежность и эффективность в технике: Справочник т.5: проектный анализ надежности / Под ред. В.И. Потушева и Л.И. Рембезы. – М.: Машиностроение, 1988 – 316 с.
5. Рябинин И.А. Логико-вероятностная теория безопасности технических систем / И.А. Рябинин, Ю.М. Парфенов, О.Д. Цыпин – Электричество, 1994 – №7 – С. 35-40.
6. Разгильдеев И.А. О надежности систем электроснабжения угольных шахт / И.А. Разгильдеев, А.П. Ковалев, Л.И. Сердюк – Уголь Украины, 1985 – №1 – С. 18-22.
7. Ковалев А.П. Применение логико-вероятностных методов для оценки надежности структурно-сложных схем / А.П. Ковалев, А.В. Спиваковский – Электричество, 2000 – №9 – С. 66-70.
8. Диллон Б. Инженерные методы обеспечения надежности систем / Б. Диллон, Ч. Сингх: Пер. с англ. – М.: Мир, 1984 – 318 с.
9. Ковалев А.П. О преобразовании звезда-треугольник
при расчетах надежности сложных по структуре схем / А.П. Ковалев, А.В. Спиваковский – Электричество, 1989 – №10 С. 70-74.
10. Голинкевич Т.А. Прикладная теория надежности / Т.А. Голинкевич – М.: изд. Высшая школа, 1977 – 135 с.
11. Бронштейн И.Н. Справочник по математике для инженеров и учащихся ВУЗов / И.Н. Бронштейн, К.А. Семендяев – М.: Наука, 1981 – 544 с.
12. Ковалев А.П. Надежность сложных по структуре невосстанавливаемых систем с учетом двух типов отказов элементов защиты / А.П. Ковалев, И.И. Лехтман научные труды Донецкого национального технического ун-та. Серия Электротехника и энергетика
№2 (15). Донецк – 2013 с. 125 – 131.
