Реферат по теме выпускной работы
Содержание
- Введение
- 1. Актуальность темы
- 2. Анализ исследований и публикаций
- 3. Результаты исследований
- 4. Пример расчета
- Выводы
- Список используемой литературы
Введение
Предложена методика оценки надежности структурно-сложных мостиковых структур
с учетом двух видов отказов средств защиты: отказ типа обрыв цепи
и отказ в срабатывании
.
Сложные мостиковые структуры
приводятся к одному эквивалентному элементу с помощью преобразования логического треугольника
в эквивалентную по надежности звезду
и обратного преобразования логического соединения в виде звезды
к эквивалентному по надежности соединению в виде треугольника
. Приведен пример расчета.
Ключевые слова:надежность, система, сложная структура, мостиковая структура, треугольник, звезда, вероятность отказов, отказ типа обрыв, отказ в срабатывании, вероятность безотказной работы.
1. Актуальность темы
К невосстанавливаемым в процессе эксплуатации системам будем относить такие системы, восстановление которых по каким-либо причинам невозможно непосредственно в рассматриваемый период времени [1]. Под сложной по структуре схемой в данном случае будем понимать такую систему, в состав которой входит хотя бы одна мостиковая структура
[2].
В тех случаях, когда необходимо повысить надежность проектируемой системы без изменения надежности комплектующих её элементов, обычно вводят избыточные (резервные) её элементы или группы элементов, либо вносятся определенные изменения в схему, что позволяет оптимизировать её структуру.
Методика оценки надежности невосстанавливаемых систем, элементы которых могут находиться только в двух несовместных состояниях: работоспособном и отказавшем (отказ типа обрыв цепи
) разработаны в достаточно полной мере [3 – 6].
Для расчета надежности невосстанавливаемых систем предполагается, что средства защиты абсолютно надежны. В реальных системах электроснабжения, газоснабжения, водоснабжения и т. д. средства защиты могут работать ложно (отказ типа обрыв цепи
), либо отказывать в срабатывании (отказ в срабатывании
).
Поэтому учет надежности средств защиты сложных по структуре схем является актуальной научно-технической задачей, решение которой позволит в значительной степени повысить точность расчетов и тем самым прогнозировать на этапе проектирования жизнеспособность разрабатываемой системы.
2. Анализ исследований и публикаций
Для оценки надежности сложных невосстанавливаемых систем, элементы которых могут находиться в трех несовместных состояниях, известны методы, основанные на использовании: разложения сложной структуры по базовому элементу, применение метода треугольник-звезда
и звезда-треугольник
, а также на использовании алгебры кортежей [3 – 6].
Полученные в этих работах формулы, не очень удобны к применению, поэтому для систем у которых вероятность отказов элементов меньше, либо равна 0,1 (к таким элементам относится и электрооборудование электрических систем и систем электроснабжения предприятий) следует использовать приближенные формулы переходов треугольник-звезда
и звезда-треугольник
и разработать принцип построения схем замещения систем электроснабжения, чтобы оценить её надежность.
Цель работы.Совершенствование методики оценки надежности систем электроснабжения промышленных предприятий с учетом двух видов отказов электрооборудования.
3. Результаты исследований
Предположим, что все рассматриваемые элементы, из которых состоит система электроснабжения, могут отказывать независимо друг от друга; каждый элемент системы может находиться в трех несовместных состояниях: работоспособном, неработоспособном – отказ обрыв цепи
,
неработоспособном – отказ в срабатывании
; потоки отказов элементов (обрыв цепи
) и отказ в срабатывании
простейшие; пропускная способность элементов неограниченна, так же как и способность сдерживать поток электроэнергии, независимо от количества короткозамкнутых элементов,
после выхода из строя элемент не восстанавливается (не заменяется на новый) в рассматриваемый период времени [7].
Обозначим через Pi вероятность безотказной работы i
-того элемента системы, qoi – вероятность появления отказов в i
-том элементе типа обрыв цепи
, а через qsi – вероятность появления отказов в i
-том элементе типа отказ в срабатывании
. Эти три состояния составляют полную группу несовместных событий.
pi+qoi+qsi=1 (1)
Индексы о
и s
в формуле (1) указывают на то, что учитываются повреждения элемента, которые приводят к отказам обрыв цепи
либо отказам в срабатывании
, соответственно.
В том случае, если в элементах системы электроснабжения наблюдается два типа несовместных отказов: отказ обрыв цепи
и отказ в срабатывании
, тогда вероятность отказов элемента i с учетом двух типов отказов, в течении времени t можно определить, пользуясь формулами [8]:
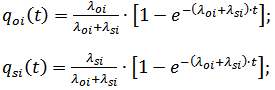
Формулы (2) и (3)
где
λoi, λsi – постоянные интенсивности отказов i
-того элемента при учете его отказов обрыв цепи
и отказов в срабатывании
, соответственно;
t – текущее время работы i
-того элемента системы.
Под простой
по структуре схемой замещения исходной системы будем понимать такую, элементы которой могут соединяться: последовательно, параллельно, последовательно-параллельно, либо параллельно-последовательно.
Для простой
по определению схемы замещения системы, которая состоит из n
логически последовательного соединения элементов, отказ типа обрыв цепи
любого из i
элементов  , приводит к разрыву связи между
, приводит к разрыву связи между входом
и её выходом
.
Если заданы вероятности отказов элементов схемы замещения qoi, то вероятность разрыва связи между входом
и её выходом
Qo определим следующим образом:
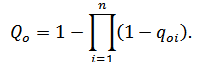
Формула (4)
В том случае, если у каждого из n
логически последовательного соединенных элементов произойдет отказ в срабатывании
в каждом из i
элементов, то это приведет к тому, что между входом
и выходом
схемы замещения пройдет сквозной аварийный ток.
Если заданы вероятности отказов элементов схемы замещения qsi, то вероятность Qs того, что между точкой входа
и выхода
схемы замещения пройдет сквозной аварийный ток, найдем с помощью формулы:
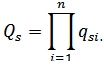
Формула (5)
Для простой по определению схемы замещения системы, которая состоит из m
логически параллельно соединенных элементов, отказ типа обрыв цепи
в каждом из j
,  элементе приводит к обрыву связи между точкой
элементе приводит к обрыву связи между точкой входа
и её выхода
.
Если заданы вероятности отказов элементов схемы замещения qoi, то вероятность Qo того, что произойдет разрыв связи между входом
и её выходом
определим с помощью формулы:
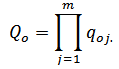
Формула (6)
В том случае, если у любого из m
логически параллельного соединения элементов произойдет отказ в срабатывании
, то это приведет к тому, что между входом
и выходом
схемы замещения пройдет сквозной аварийный ток.
Если заданы вероятности отказов qsj,  элементов схемы замещения, которая состоит из
элементов схемы замещения, которая состоит из m
логически параллельного соединения элементов, тогда Qs – вероятность того, что между точкой входа
и выхода
схемы замещения пройдет сквозной аварийный ток, найдем, используя формулу:
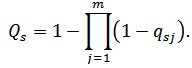
Формула (7)
Чтобы сложную
схему замещения системы электроснабжения привести к простой по определению, следует использовать способ переходов от логического треугольника
к эквивалентной по надежности звезде
, либо использовать способ переходов от логической звезды
к эквивалентному по надежности логическому треугольнику
(рис. 1 а, б).

Рис. 1. Логическое соединение элементов в виде: а) треугольника
; б) звезды
(анимация: 7 кадров, 8 циклов, 36 килобайт)
Точные формулы переходов от логического треугольника
к эквивалентной по надежности звезде
(рис. 1а, б) и от логической звезды
к эквивалентному по надежности логическому треугольнику
(рис. 1б, а) приведены в [8,9].
Пусть каждый элемент логического треугольника
обозначим их символами x,y,z (рис. 1а) характеризуются вероятностями Pox,qsx; Poy,qsy; Poz,qsz, а элементы i, j, k логической звезды вероятностями Poi,qsi; Poj,qsj; Pok,qsk (рис. 1б).
Сущность преобразования логического треугольника
в эквивалентную по надежности логическую звезду
заключается в том, что соединение (рис. 1а) заменяется на эквивалентное по надежности соединение в виде (рис. 1б).
Если заданы параметры надежности элементов логического треугольника
Pox,Poy,Poz и qsx,qsy,qsz, то эквивалентные по надежности параметры звезды
qoi,qoj,qok и qsi,qsj,qsk находим пользуясь формулами [8]:

Формулы (8) (9) (10)
Отсюда:
qoi=1-Poi; qoj=1-Poj; qok=1-Pok.

Формулы (11) (12) (13)
Для высоконадежных систем, для которых соблюдается условие:

Формула (14)
Формулы (10) – (15) примут вид [10]:
Poi=1-(1-Pox)(1-Poy); (15)
Poj=1-(1-Poy)(1-Poz); (16)
Pok=1-(1-Pox)(1-Poz). (17)

Формулы (18) (19) (20)
Формулы (8) – (13) и (15) – (20) позволяют логический треугольник
заменить на эквивалентную по надежности звезду
используя точные и приближенные формулы.
Если заданы параметры надежности элементов логической звезды
(рис. 1б): Poi, qsi; Poj, qsj; Pok, qsk, то эквивалентные по надежности элементы – треугольника
Pox, qsx; Poy, qsy; Poz ,qsz (рис. 1а) найдем пользуясь формулами [9]:

Формулы (21) (22) (23)
Параметр t в формулах (21) – (23) находится из решения кубического уравнения вида:

Формула (24)
где –

Формула (25)
где
a=qoi+qok-qoi×qok;
b=qoi+qoj-qoi×qoj; (26)
c=qoj+qok-qoj×qok.
В кубическом уравнении (24) производится замена [11]:

Формула (27)
Уравнение (24) примет вид:

Формула (28)
где

а) если α6≤0 и α4≤0 тогда:

Формулы (29) (30) (31)

б) если α6≥0 и α4≤0 тогда:

Формулы (32) (33) (34)
где

Подставляя найденные значения:  в формулу (27) получим:
в формулу (27) получим:

Формулы (35) (36) (37)
Подставляются поочередно найденные корни t1, t2, t3 в формулы (21) – (23) и выбирается тот корень, для которого выполняется условие:
0<qox<1; 0<qoy<1; 0<qoz<1; (38)
Формулы переходов от соединения в виде звезды
к эквивалентному по надежности соединению в виде треугольника
при учете отказов элементов типа короткое замыкание
примут вид:

Формулы (39) (40) (41)
Значение корней кубического уравнения (42) t1, t2, t3 находим из его решения.
Коэффициенты кубического уравнения α1, α2, α3 находятся с помощью формул (25), а коэффициенты a, b и c определяются по формулам:
a=Psi+Psk-Psi×Psk
b=Psi+Psj-Psi×Psj (43)
c=Psj+Psk-Psj×Psk
Выбирается то значение корня, при котором:
0<qsx<1; 0<qsy<1; 0<qsz<1; (44)
Для высоконадежных систем формулы переходов от логической звезды
к эквивалентному по надежности соединению в виде треугольника
примут вид [12]:

Формулы (45) (46) (47)
qsi=qsk; (48)
qsy=qsi×qsj; (49)
qsz=qsx×qsj. (50)
Формулы (21) – (23), (39) – (41) и (45) – (50) позволяют логическую звезду
заменить на эквивалентный по надежности логический треугольник
, используя точные и приближенные формулы.
Для невосстанавливаемой системы справедлива формула [8]:
R=1-Qo-Qs, (51)
4. Пример расчета
Пример. Для схемы замещения системы, изображенной на рисунке 2, заданы следующие вероятности отказов: qo1=0,12; qs1=0,25; qo2=0,35; qs2=0,23; qo3=0,22; qs3=0,42; qo4=0,18; qs4=0,18:

Рис. 2 – Мостиковая структура
Определить вероятность того, что не произойдет разрыв связи и не пройдет сквозной аварийный ток между входом
и выходом
схемы замещения.
Решение. К логическому треугольнику
АВС применил преобразование треугольник-звезда
, используя формулы (8) – (13), находим:
qo6=0,0216; qs6=0,686;
qo7=0,038; qs7=0,47;
qo8=0,074; qs8=0,661.
Схема рис. 2, преобразуется в схему смешанной структуры рис. 3:

Рис 3. – Схема замещения простой структуры
Используя схему рис. 3 и формулы (4) – (7) находим:

Используя формулу (51) находим:
R=1-Qo-Qs=1-0,087-0,134=0,78.
Анализ результатов можно получить, если использовать метод разложения сложной структуры (рис. 2) по базовому элементу [7].
В качестве базового элемента в схеме рис. 2 выберем элемент 2, тогда схема преобразуется в две новые рис. 4 (а, б):

Рис. 4 – Схемы преобразования (а, б)
Используя теорему о сумме вероятности несовместных событий находим:

Используя формулу (51) находим:
R=Ro-Qo=0,912-0,13=0,78.
Выводы
1. Предложена методика оценки надежности сложных по структуре схем систем электроснабжения, элементы которых могут находиться в трех несовместных состояниях.
2. Предлагаемую методику
целесообразно использовать для случая когда: qoi≤0,1 и qsi≤0,1 где  .
.
Список используемой литературы
1. Козлов Б.А. Справочник по расчету надежности аппаратуры радиоэлектроники и автоматики / Б.А. Козлов, И.С. Ушаков – М.: Советское радио, 1975 – 472 с.
2. Ковалев А.П. Метод расчета надежности сложных систем электроснабжения с учетом восстановления элементов / А.П. Ковалев, Л.И. Сердюк – Электричество, 1985 – №10 – С. 52-53.
3. Рябинин И.А. Основы теории и расчета надежности судовых электроэнергетических систем / И.А. Рябинин – 2-е изд. – Л.: Судостроение, 1971. – 456с.
4. Надежность и эффективность в технике: Справочник т.5: проектный анализ надежности / Под ред. В.И. Потушева и Л.И. Рембезы. – М.: Машиностроение, 1988 – 316 с.
5. Рябинин И.А. Логико-вероятностная теория безопасности технических систем / И.А. Рябинин, Ю.М. Парфенов, О.Д. Цыпин – Электричество, 1994 – №7 – С. 35-40.
6. Разгильдеев И.А. О надежности систем электроснабжения угольных шахт / И.А. Разгильдеев, А.П. Ковалев, Л.И. Сердюк – Уголь Украины, 1985 – №1 – С. 18-22.
7. Ковалев А.П. Применение логико-вероятностных методов для оценки надежности структурно-сложных схем / А.П. Ковалев, А.В. Спиваковский – Электричество, 2000 – №9 – С. 66-70.
8. Диллон Б. Инженерные методы обеспечения надежности систем / Б. Диллон, Ч. Сингх: Пер. с англ. – М.: Мир, 1984 – 318 с.
9. Ковалев А.П. О преобразовании звезда-треугольник
при расчетах надежности сложных по структуре схем / А.П. Ковалев, А.В. Спиваковский – Электричество, 1989 – №10 С. 70-74.
10. Голинкевич Т.А. Прикладная теория надежности / Т.А. Голинкевич – М.: изд. Высшая школа, 1977 – 135 с.
11. Бронштейн И.Н. Справочник по математике для инженеров и учащихся ВУЗов / И.Н. Бронштейн, К.А. Семендяев – М.: Наука, 1981 – 544 с.
12. Ковалев А.П. Надежность сложных по структуре невосстанавливаемых систем с учетом двух типов отказов элементов защиты / А.П. Ковалев, И.И. Лехтман научные труды Донецкого национального технического ун-та. Серия Электротехника и энергетика
№2 (15). Донецк – 2013 с. 125 – 131.
