Реферат за темою випускної роботи
Зміст
- Вступ
- 1. Актуальність теми
- 2. Аналіз досліджень і публікацій
- 3. Результати досліджень
- Висновки
- Список використаної літератури
Вступ
Запропонована методика оцінки надійності структурно-складних мостикових структур
з урахуванням двох видів відмов засобів захисту: відмова типу обрив ланцюга
і відмова в спрацьовуванні
.
Складні мостикові структури
приводяться до одного еквівалентному елементу за допомогою перетворення логічного трикутника
в еквівалентну по надійності зірку
і зворотного перетворення логічного з'єднання у вигляді зірки
до еквівалентного по надійності з'єднання у вигляді трикутника»
.
Ключові слова:надійність, система, складна структура, мостикова структура, трикутник, зірка, ймовірність відмов, відмова типу обрив, відмова в спрацьовуванні, ймовірність безвідказної роботи.
1. Актуальність теми
До невідновлюваних в процесі експлуатації систем будемо відносити такі системи, відновлення яких з будь-яких причин неможливо безпосередньо на даний період часу [1]. Під складною за структурою схемою в даному випадку будемо представляти таку систему, до складу якої входить хоча б одна мостикова структура
[2].
У тих випадках, коли необхідно підвищити надійність проектованої системи без зміни надійності комплектуючих її елементів, зазвичай вводять надмірні (резервні) її елементи або групи елементів, або вносяться певні зміни в схему, що дозволяє оптимізувати її структуру.
Методика оцінки надійності невідновлюваних систем, елементи яких можуть знаходитися тільки в двох несумісних станах: працездатному і тому, що відмовляє (відмова типу обрив ланцюга
), розроблені в досить повній мірі [3 – 6].
Для розрахунку надійності невідновлювальних систем передбачається, що засоби захисту абсолютно надійні. У реальних системах електропостачання, газопостачання, водопостачання і т. д. Засоби захисту можуть працювати помилково (відмова типу обрив ланцюга
), або відмовляти в спрацьовуванні (відмова в спрацьовуванні
).
Тому облік надійності засобів захисту складних за структурою схем є актуальним науково-технічним завданням, рішення якого дозволить в значній мірі підвищити точність розрахунків і тим самим прогнозувати на етапі проектування життєздатність системи, що розробляється.
2. Аналіз досліджень і публікацій
Для оцінки надійності складних невідновлювальних систем, елементи яких можуть знаходитися в трьох несумісних станах, відомі методи, основані на використанні: розкладання складної структури по базовому елементу, застосування методу трикутник-зірка
і зірка-трикутник
, а також на використанні алгебри кортежів [3 – 6].
Отримані в цих роботах формули, не дуже зручні для застосування, тому для систем, у яких ймовірність відмов елементів менше, або дорівнює 0,1 (до таких елементів відноситься і електрообладнання електричних систем і систем електропостачання підприємств) слід використовувати приближені формули переходів трикутник-зірка
і зірка-трикутник
і розробити принцип побудови схем замінення систем електропостачання, щоб оцінити її надійність.
Мета роботи.Удосконалення метода оцінки надійності систем електропостачання промислових підприємств з урахуванням двох видів відмов електрообладнання.
3. Результати досліджень
Припустимо, що всі розглянуті елементи, з яких складається система електропостачання, можуть відмовляти незалежно один від одного; кожен елемент системи може знаходитися в трьох несумісних станах:
працездатному, непрацездатному – відмова обрив ланцюга
, непрацездатному – відмова в спрацьовуванні
; потоки відмов елементів (обрив ланцюга
) і відмова в спрацьовуванні
найпростіші; пропускна здатність елементів необмежена, так само як і здатність стримувати потік електроенергії, незалежно від кількості короткозамкнутих елементів, після виходу з ладу елемент не відновлюється (не замінювати на новий) у розглянутий період часу [7].
Позначимо через Pi ймовірність безвідмовної роботи i
-того елемента системи, qoi – ймовірність появи відмов в i
– тому елементі типу обрив ланцюга
, а через qsi – ймовірність появи відмов в i
– тому елементі типу відмова у спрацьовуванні
. Ці три стани складають повну групу несумісних подій.
pi+qoi+qsi=1 (1)
Індекси о
і s
у формулі (1) вказують на те, що враховуються пошкодження елемента, які призводять до відмов обрив ланцюга
або відмов в спрацьовуванні
.
У тому випадку, коли в елементах системи електропостачання спостерігається два типи несумісних відмов: відмова обрив ланцюга
і відмова в спрацьовуванні
, тоді ймовірність відмов елемента i з урахуванням двох типів відмов, в протягом часу t можна визначити, користуючись формулами [8]:
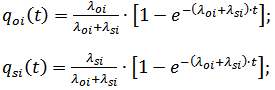
Формули (2) и (3)
де
λoi, λsi – постійні інтенсивності відмов i
-того елемента при врахуванні його відмов обрив ланцюга
і відмов в спрацьовуванні
, відповідно;
t – поточний час роботи i
-того елемента системи.
Під простою
за структурою схемою заміщення вихідної системи будемо розуміти таку, елементи якої можуть з'єднуватися: послідовно, паралельно, послідовно-паралельно або паралельно-послідовно.
Для простої
за структурою схеми заміщення системи, яка складається з n
логічно послідовного з'єднання елементів, відмова типу обрив ланцюга
будь-якого з i
елементів  , призводить до розриву зв'язку між
, призводить до розриву зв'язку між входом
і її виходом
.
Якщо задані ймовірності відмов елементів схеми заміщення qoi, то ймовірність розриву зв'язку між входом
і її виходом
Qo визначимо наступним чином:
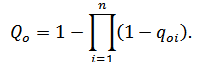
Формула (4)
У тому випадку, якщо у кожного з n
логічно послідовного з'єднаних елементів відбудеться відмова в спрацьовуванні
в кожному з i
елементів, то це призведе до того, що між входом
і виходом
схеми заміщення пройде наскрізний аварійний струм.
Якщо задані ймовірності відмов елементів схеми заміщення qsi, то ймовірність Qs того, що між точкою входу
і виходу
схеми заміщення пройде наскрізний аварійний струм, знайдемо за допомогою формули:
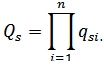
Формула (5)
Для простої за визначенням схеми заміщення системи, яка складається з m
логічно паралельно з'єднаних елементів, відмова типу обрив ланцюга
в кожному з j
,  елементі призводить до обриву зв'язку між точкою
елементі призводить до обриву зв'язку між точкою входу
і її виходу
.
Якщо задані ймовірності відмов елементів схеми заміщення qoi, то ймовірність Qo того, що станеться розрив зв'язку між входом
і її виходом
визначимо за допомогою формули:
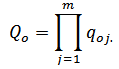
Формула (6)
У тому випадку, якщо у будь-якого з m
логічно паралельного з'єднання елементів відбудеться відмова в спрацьовуванні
, то це призведе до того, що між входом
і виходом
схеми заміщення пройде наскрізний аварійний струм.
Якщо задані ймовірності відмов qsj,  елементів схеми заміщення, яка складається з
елементів схеми заміщення, яка складається з m
логічно паралельного з'єднання елементів, тоді Qs – ймовірність того, що між точкою входу
і виходу
схеми заміщення пройде наскрізний аварійний струм, знайдемо, використовуючи формулу:
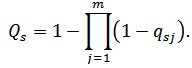
Формула (7)
Щоб складну
схему заміщення системи електропостачання привести до простої за визначенням, слід використовувати спосіб переходів від логічного трикутника
до еквівалентної по надійності зірці
, або використовувати спосіб переходів від логічної зірки
до еквівалентного по надійності логічного трикутнику
(рис. 1 а, б).

Мал. 1. Логічне з'єднання елементів у вигляді: а) трикутника
; б) зірки
(анімація: 7 кадрів, 8 циклів, 36 кілобайт)
Точні формули переходів від логічного трикутника
до еквівалентної по надійності зірці
(рис. 1а, б) і від логічної зірки
до еквівалентного по надійності логічного трикутнику (рис. 1б, а) представлені в [8,9].
Висновки
1. Запропонована методика оцінки надійності складних за структурою схем систем електропостачання, елементи яких можуть знаходитися в трьох несумісних станах.
2. Запропоновану методику
доцільно використовувати для випадку коли: qoi≤0,1 і qsi≤0,1, де  .
.
Список використаної літератури
1. Козлов Б.А. Справочник по расчету надежности аппаратуры радиоэлектроники и автоматики / Б.А. Козлов, И.С. Ушаков – М.: Советское радио, 1975 – 472 с.
2. Ковалев А.П. Метод расчета надежности сложных систем электроснабжения с учетом восстановления элементов / А.П. Ковалев, Л.И. Сердюк – Электричество, 1985 – №10 – С. 52-53.
3. Рябинин И.А. Основы теории и расчета надежности судовых электроэнергетических систем / И.А. Рябинин – 2-е изд. – Л.: Судостроение, 1971. – 456с.
4. Надежность и эффективность в технике: Справочник т.5: проектный анализ надежности / Под ред. В.И. Потушева и Л.И. Рембезы. – М.: Машиностроение, 1988 – 316 с.
5. Рябинин И.А. Логико-вероятностная теория безопасности технических систем / И.А. Рябинин, Ю.М. Парфенов, О.Д. Цыпин – Электричество, 1994 – №7 – С. 35-40.
6. Разгильдеев И.А. О надежности систем электроснабжения угольных шахт / И.А. Разгильдеев, А.П. Ковалев, Л.И. Сердюк – Уголь Украины, 1985 – №1 – С. 18-22.
7. Ковалев А.П. Применение логико-вероятностных методов для оценки надежности структурно-сложных схем / А.П. Ковалев, А.В. Спиваковский – Электричество, 2000 – №9 – С. 66-70.
8. Диллон Б. Инженерные методы обеспечения надежности систем / Б. Диллон, Ч. Сингх: Пер. с англ. – М.: Мир, 1984 – 318 с.
9. Ковалев А.П. О преобразовании звезда-треугольник
при расчетах надежности сложных по структуре схем / А.П. Ковалев, А.В. Спиваковский – Электричество, 1989 – №10 С. 70-74.
10. Голинкевич Т.А. Прикладная теория надежности / Т.А. Голинкевич – М.: изд. Высшая школа, 1977 – 135 с.
11. Бронштейн И.Н. Справочник по математике для инженеров и учащихся ВУЗов / И.Н. Бронштейн, К.А. Семендяев – М.: Наука, 1981 – 544 с.
12. Ковалев А.П. Надежность сложных по структуре невосстанавливаемых систем с учетом двух типов отказов элементов защиты / А.П. Ковалев, И.И. Лехтман научные труды Донецкого национального технического ун-та. Серия Электротехника и энергетика
№2 (15). Донецк – 2013 с. 125 – 131.
