Содержание
- Введение
- 1. Актуальность темы
- 2. Цель работы
- 3. Анализ структуры системы
- 3.1 Обоснование выбора и принцип действия датчика
- 3.2 Обоснование выбора структурной схемы
- 4. Методы программного определения амплитуды
- 4.1 Дискретное преобразование Фурье(ДПФ)
- 4.2 Среднеквадратичное значение
- 4.3 Тригонометрическая апроксимация
- 4.4 Выбор метода определения амплитуды
- Вывод
- Список источников
Введение
В последнее время на хлебоизготовительных предприятиях все большую популярность приобретает бестарный метод хранения муки. Причина повышения популярности бестарного метода в том, что бестарное хранение и транспортировка муки (БХМ) по сравнению с тарным способом хранения и транспортировки имеет ряд преимуществ:
- исключение тяжелых физических работ, весь процесс механизирован;
- возможна автоматизация процесса (Автоматизация складов БХМ);
- экономия на таре (мешках);
- уменьшается распыл (потери) муки;
- мука аэрируется, улучшается ее качество;
- улучшается санитарное состояние производства хлебобулочных изделий;
- снижаются эксплуатационные расходы;
- для крупных и средних хлебобулочных предприятий экономится электроэнергия;
- экономится площадь.
1. Актуальность темы
Прибыль предприятия в немалой степени зависит от того, по какой цене и в каком количестве закуплена мука и как рационально она израсходована. Кроме того, субъективная оценка количества муки дает большую погрешность определения остатков (до двух-трех тонн на силос). Дело в том, что различные сорта муки имеют разную плотность, и если ржаной муки в силос можно загрузить до 30-31 тонны, то муки высшего сорта – до 35 тонн. Кроме того, в процессе откачки муки в нижней конусообразной части силоса образуются пустоты, порой большие по объему, которые не просматриваются сверху сквозь толщу муки даже с фонарем. Вот почему, важное значение приобретает автоматизация задачи сменного и суточного учета прихода-расхода муки. В проекте хлебозаводов, вводившихся в эксплуатацию в начале 70-х годов, такая автоматизация предусматривалась на основе технических средств, имевшихся в то время. На одних заводах автоматизация внедрялась, но плохо работала или не работала совсем, на других заводах не внедрялась, хотя была предусмотрена в проекте.
2. Цель работы
Целью работы является разработка системы, позволяющей в режиме реального времени отслеживать количество муки в каждом силосе, с помощью современных аппаратно-программных средств.
3. Анализ структуры системы
Основная идея построения системы заключается том, чтобы по заданному расписанию, либо по требованию оператора, фиксировать текущее значение веса силосов, и сохранять его в базу данных.
3.1 Обоснование выбора и принцип действия датчика
В качестве первичного измерительного преобразователя выбран магнитоанизотропный датчик. Достоинствами магнитоанизотропных преобразователей силы являются высокие чувствительность и собственная частота колебаний, мощность и уровень выходного сигнала, достаточно хорошая точность измерения, надежность конструкции, простота и дешевизна изготовления, низкая чувствительность к температуре окружающей среды.[1]
Принцип действия магнитоанизотропных датчиков заключается в следующем. Под влиянием внешних механических напряжений, магнитные свойства материала претерпевают изменения во всех направлениях с различной интенсивностью и различными знаками, в зависимости от величины внешнего магнитного поля, т.е. магнитная анизотропия материала изменяется. На этом и основан принцип действия магнитоанизотропных датчиков.
Датчики устроены следующим образом. В замкнутом магнитопроводе расположены две взаимно перпендикулярные обмотки (рис.1). Для этой цели в магнитопроводе для обмоток делаются четыре отверствия, расположенные симметрично по углам квадрата или прямоугольника. Каждая из обмоток укладывается в два диагонально противоположных отверстия. Измеряемая нагрузка прикладывается под углом 45°к плоскости каждой обмотки.
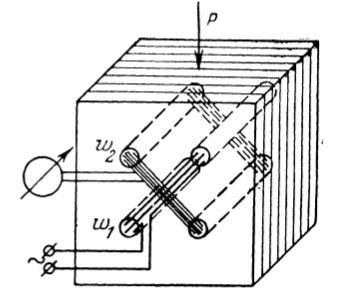
Рисунок 1 – Магнитоанизотропный датчик
Намагничивающая обмотка ω1 питается переменным током, ко второй обмотке ω2 (измерительной), подключается измерительный прибор, или другой чувствительный орган.
При протекании переменного тока по намагничивающей обмотке, создается магнитный поток, характер распределения которого показан на рис.2.[2]
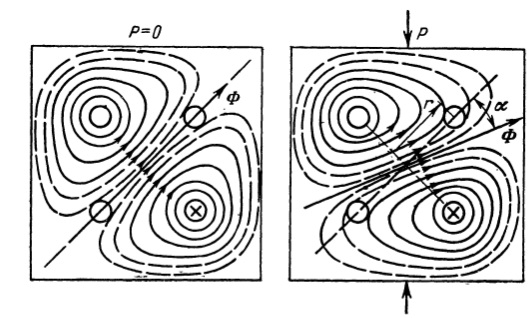
Рисунок 2 – Характер распределения магнитного потока в датчике
Если магнитопровод датчика выполнен из магнитноизотропного материала и отверстия расположены симметрично, то при отсутствии нагрузки, магнитные линии потока, замыкаясь, не пересекают измерительную обмотку и, следовательно, не индуцируют в ней э.д.с.
3.2 Обоснование выбора структурной схемы
Один из вариантов построения структурной схемы представлен на рис.3

Рисунок 3 – Структурная схема
В данной структурной схеме блок питания представляет собой генератор синусоидального сигнала, с частотой генерации, равной 400 Гц, питаемый от сети.
Блок системы датчиков состоит из всех датчиков используемых в системе, их обмотки возбуждения подключены параллельно, а измерительные обмотки подключены последовательно по четыре, соответственно датчикам, используемым для взвешивания одного силоса, и параллельно по отношению к остальным. Выход каждой группы из четырех датчиков подключается к делителю напряжения, так как сумма выходных сигналов датчика может достигать очень больших значений.
С делителя напряжения, сигнал подается на измерительный усилитель, который представляет собой двухкаскадный дифференциальный усилитель на трех операционных усилителях. Он обеспечивает эффективное подавление синфазной помехи, а так же имеет очень высокое входное напряжение, и низкое выходное. Затем сигнал выпрямляется при помощи прецизионного выпрямителя, который представляет собой двухполупериодный детектор средневыпрямленного напряжения с одним выпрямляющим узлом. Выпрямленный сигнал подается на активный фильтр низких частот второго порядка, который, одновременно с тем, является так же масштабирующим преобразователем и выполняет одновременно три функции:
- подавление высокочастотной помехи;
- сглаживание выпрямленного сигнала;
- приведение дипазона изменения выходного сигнала к диапазону измерения АЦП;
С ФНЧ сигнал передается к микроконтроллеру со встроенным АЦП, в котором значение напряжения преобразуется в значение веса силоса и выводится на терминал и в базу данных предприятия. Опрос силоса может производиться как в плановом режиме, с заданной периодичностью, так и по требованию оператора.
Однако, задачу определения амплитуды сигнала можно решить и иным способом. Структурная схема альтернативного метода приведена на рис.4:

Рисунок 4 – Альтернативная структурная схема измерительного канала
Где МП – масштабирующий преобразователь.
В данной схеме предполагается, что сигнал датчика преобразуется в удобную для оцифровки форму при помощи МП и подается на аналоговый вход микроконтроллера. При такой схеме, на вход микроконтроллера действует гармонический сигнал, и потому использование мгновенного значения не имеет смысла, однако, если произвести серию замеров, и сформировать из результатов замеров массив временных отсчетов, то становится возможным программное определение амплитуды измеряемого сигнала. На рис.5 приведен пример реализации данного метода:
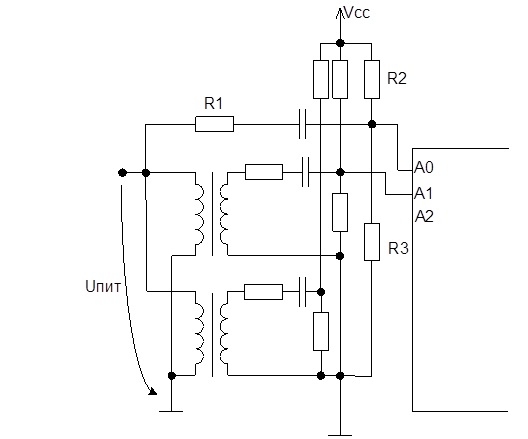
Рисунок 5 – Схемотехническая реализация алтернативного метода
В качестве датчиков тут выступают магнитоанизотропные датчики давления, которые обозначены как трансформаторы. Поскольку данные датчики дают высокое значение амплитуды сигнала, в качестве масштабирующего преобразователя можно применить резистивный делитель. Однако, если просто снизить амплитуды сигнала, то на вход микроконтроллера поступит только полуволна синусоиды. Для того, чтобы МК правильно принимал сигнал, необходимо создать смещение. Таким образом, резисторы R2 и R3 задают постоянное смещение равное половине от максимального уровня воспринимаемое МК, а R1 и R3 являются делителем напряжения, которое снижает амплитуду сигнала. Таким образом на вход МК действует сигнал, осцилограмма которого приведена на рис.6:
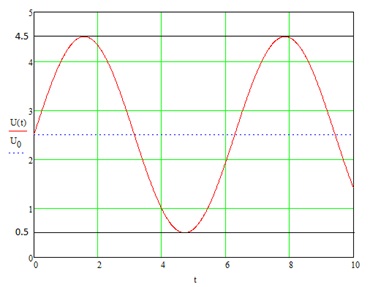
Рисунок 6 – Осцилограмма входного сигнала
На рис.6. видно, что постоянное смещение сигнала составляет 2.5В, а максимально допустимая амплитуда входного сигнала составляет 2В.
Таким образом, при реализации альтернативного метода построения измерительного канала, становится возможным достижение ряда преимуществ:
- Серьезное упрощение аппаратной части;
- Увеличение надежности схемы, за счет снижения числа компонентов, входящих в ее состав;
- Исключение погрешностей, вносимых измерительным каналом;
- Полное исключение высокочастотных и низкочастотных погрешностей;
- Увеличение быстродействия системы, за счет того, что в ФНЧ, для получения постоянного уровня сигнала, нужен конденсатор большой емкости, из-за чего время проведения замера может составлять до 0,2 с.;
- Замер происходит не только амплитуды на измерительной обмотке датчика, но и на питающей обмотке, что позволяет так же отслеживать изменения питающего напряжения датчика, и вносить коррекцию в обработку результатов. Это существенно снижает требования к точности обеспечения амплитуды генератора питающего сигнала.;
4. Методы программного определения амплитуды
В случае, когда требуется программно определить амплитуду гармонического сигнала из массива временных отсчетов, важной задачей является выбор метода, который лучше всего подходит для этого, исходя из условий, при которых массив отсчетов был сформирован. Так например метод прямого определения размаха гармоники, путем определения максимального и минимального значения в массиве, будет иметь высокую погрешность, если в сигнале будет присутствовать помеха, либо если на один период гармоники будет приходиться недостаточное число точек.
Рассмотрим несколько методов определения амплитуды гармонического сигнала, а так же их преимущества и недостатки.
4.1 Дискретное преобразование Фурье(ДПФ)
В общем случае, ДПФ применяется для спектрального анализа сигналов, и имеет вид[3]:
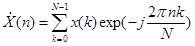 (1)
(1)Однако в данном случае нас интересует не спектр сигнала, а всего лишь один спектральный отсчет, и потому, вычислять ДПФ для всего спектра нецелессобразно, тем более, что это может занять достаточно большое количество времени. По этой причине, вместо полного, стоит использовать ДПФ для одного спектрального отсчета.
Для реализации такого подхода, следует выбрать период дискретизации сигнала таким образом, чтобы в одном периоде сигнала было целое число временных отсчетов. В таком случае, номер искомой гармоники будет равен как раз числу временных отсчетов, приходящихся на период сигнала.
При этом, важно понимать, что полученное в результате ДПФ значение амплитуды сигнала будет пропорционально отличаться от реальной амплитуды сигнала. Для установлений этой пропорции, следует так же произвести ДПФ для нулевой гармоники. Полученное значение нулевой гармоники используем в качестве опорного значения, т.к. известно, что оно соответствует удвоенному значению постоянной составляющей. Тогда формула определения амплитуды искомой гармоники:
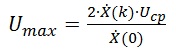 (2)
(2)Где k – номер искомой гармоники
Преимущества данного метода заключаются в том, что можно с высокой точностью определить значение амплитуды сигнала, при этом полностью игнорируя весь спектр сигнала, кроме единственной частоты, что удобно в ситуациях, когда имеют место быть наводки, либо высокочастотные шумы.
Однако, для того, чтобы выполнить условие целого числа временных отсчетов на период сигнала, нужно очень точно знать частоту данной гармоники(с точностью не хуже 0,01%), иначе, в силу очень высокой крутизны характеристики, будет большая погрешность. Поэтому данный метод подходит только в тех случаях, когда есть возможность заранее с высокой точностью определить частоту сигнала, либо когда сигнал генерируется источником с очень высокой стабильностью частоты.
4.2 Среднеквадратичное значение
В данном методе, амплитудное значение гармоники определяется по формуле[4]:
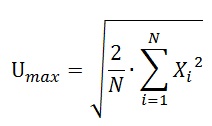 (3)
(3)Важной особенностью метода является то, что для достижения максимальной точности, рекомендуется использовать целое число периодов сигнала, однако при помощи программных средств можно легко определить в массиве точки, которые удобнее всего принимать за начальную и конечную.
Кроме того, важной особенностью является то, что для реализации данного метода не обязательно задавать сигналу постоянное смещение, чтобы весь размах гармоники входил в диапазон измерения АЦП. Напротив, можно пропустить сигнал через разделительный конденсатор, либо ФВЧ перед оцифровкой. Для полученного однополупериодного сигнала амплитуда равна:
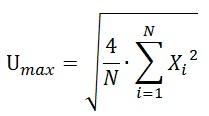 (4)
(4)Такой подход может оказаться полезным, если используется АЦП с малой разрядностью, т.к. весь диапазон АЦП может работать на одну полуволну гармоники, вместо полного размаха.
4.3 Тригонометрическая апроксимация
В основе данного метода лежит идея интерполяции полиномом Фурье, который имеет вид[5]:
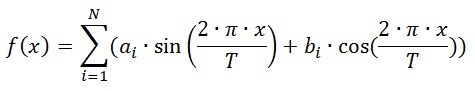 (5)
(5)Однако использование такого полинома мало чем отличается по смыслу от обычного анализа Фурье, и при учете того, что предполагаемый сигнал гармонический, для получения амплитуды сигнала, достаточно программно исключить постоянную составляющую из сигнала и рассчитать коэффициент a по формуле:
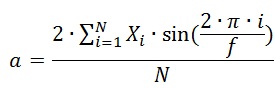 (6)
(6)Как и в случае с ДПФ, для реализации данного метода необходимо заранее знать частоту сигнала, однако требования к точности тут значительно ниже(точность определения частоты должна быть не хуже 0,1%). Кроме того, важно следить за тем, чтобы фаза аппроксимирующей синусоиды совпадала с фазой исследуемой гармоники. Так же, для максимальной точности, следует выбирать из исходного массива данных такой фрагмент для анализа, при котором первой точкой будет начало периода, а последней – конец периода.
Одним из важных преимуществ метода является компенсация погрешности квантования, так при моделировании данного алгоритма, обнаружено, что гармонический сигнал, оцифрованный при помощи 32 уровней квантования, может быть восстановлен с точностью до десятых долей процента, если на один период сигнала приходится не менее сотни точек.
4.4 Выбор метода определения амплитуды
Так как датчик имеет большое значение выходного напряжения, соотношение сигнал-шум достаточно высоко и потому нет нужды в использовании сложных алгоритмов позволяющих игнорировать шумы. Поэтому, более рациональным выглядит метод определения среднеквадратичного значения. Кроме того, одним из преимуществ альтернативной схемы построения измерительного канала является снижение требований к аппаратной части, чему данный метод так же способствует, так как при нем отсутствует необходимость в точном значении частоты измеряемого сигнала, достаточно только того, чтобы начальная и конечная точки интервала исследования были равны среднему уровню сигнала(для двухполупериодного).
Вывод
В данной работе был описан метод осуществления учета расхода муки. Выбран датчик, при помощи которого будет определяться значение массы силоса и предложено два варианта построения измерительного канала. Так же, для варианта измерительного канала опирающегося на программное определение значения выходного сигнала датчика, проведен обзор трех методов вычисления амплитуды сигнала и выбран тот, который является более рациональным исходя из условий поставленной задачи.
При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: июнь 2018 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Список источников
- Дубинин, А.Е. Магнито-анизотропные преобразователи силы / А.Е. Дубинин.– М.: Энерноатомиздат, 1991.– 112с.
- Шевченко, Г.И. Магнито-анизотропные датчики / Г.И. Шевченко.– М.: Энергия, 1967.– 73 с.
- Александров, В.А. Преобразование Фурье: Учеб. пособие / В.А. Александров.– Новосибирск: НГУ, 2002.– 62 с.
- Фано, Р. Передача информации. Статическая теория связи / Р. Фано; пер. с анг. И.А.Овсеевича и М.С. Пинскера, науч. ред. Р.Л.Добрушина.– М.: Мир, 1965.– 440 с.
- Вержбицкий, В.М. Численные методы / В.М. Вержбицкий.– М.: Высшая школа, 2001.– 382с.
- Бауманн, Э. Измерение сил электрическими методами / Э. Бауманн; пер. с нем. А.С. Вишенкова и С.Н. Герасимова, науч. ред. И.И. Смыслова.– М.: Мир, 1978.– 423с.
