Реферат по теме выпускной работы
Содержание
- Введение
- 1. Актуальность темы
- 2. Цель и задачи исследования, планируемые результаты
- 3. Теоретический раздел
- 3.1. Алгоритм получения
минимальных сечений
при учете отказов элементов схемы замещения типаобрыв цепи
- 3.2. Алгоритм получения
минимальных сечений
при учете отказов всрабатывании
элементов схемы замещения - 4. Практический раздел
- Выводы
- Список используемой литературы
Введение
Элементы с тремя несовместными состояниями: работоспособное, отказ типа обрыв цепи
и отказ типа короткое замыкание
можно выделить в системах: электроснабжения, газоснабжения, водоснабжения и т.д. Аналогами элементов с тремя несовместными состояниями в таких системах могут быть защитные коммутационные аппараты, краны, вентили различных типов, запорная арматура, заглушки и другие виды прерывателей потока (электроэнергии, газа, жидкости, информации и т.д.), для которых в неработоспособном состоянии поток не прерывается (короткое замыкание
) или не передается (обрыв цепи
) [3].
В тех случаях, если необходимо повысить надежность проектируемой системы без изменения надежности комплектующих ее элементов обычно вводят избыточные (резервные) элементы, либо изменяют структурную схему сети. Для систем, состоящих из элементов, которые могут находиться в трех несовместных состояниях, введение избыточных элементов с тремя состояниями может не только не увеличить ее надежность, но даже снизить. Все будет зависеть от соотношения между различными видами отказов элемента схемы, ее конфигурации и числа резервных элементов или их групп.
1. Актуальность темы
Разработка новых и усовершенствование существующих методов оценки надежности невосстанавливаемых систем, элементы которых могут находиться в трех несовместных состояниях, является актуальной научной проблемой, решение которой позволит значительно повысить точность прогноза их надежности, как на этапе проектирования, так и на этапе реконструкции и эксплуатации.
2. Цель и задачи исследования, планируемые результаты
Целью магистерской работы является обзор одного из существующих методов оценки надежности невосстанавливаемых, сложных по структуре систем, элементы которых могут находиться в трех несовместных состояниях – метода Минимальных сечений
.
Основные задачи исследования:
- Обзор литературных источников и определение существующих методов оценки надежности невосстанавливаемых, сложных по структуре систем, элементы которых могут находиться в трех несовместных состояниях.
- Разбор метода
Минимальных сечений
. - Применение данного метода расчета на конкретном примере.
Планируемые результаты:
- Определение точности расчета надежности невосстанавливаемых структурно-сложных схем для t ≤ 0,1 год, предлагаемым способом с использованием схем
минимальных сечений
. - Сравнение точности расчета с другими известными методами расчета оценки надежности невосстанавливаемых систем, элементы которых могут находиться в трех несовместных состояниях.
3. Теоретический раздел
К невосстанавливаемой системе будем относить такую, работоспособность которой в случае возникновения отказа не подлежит восстановлению в рассматриваемых условиях [1].
Под системой в данном случае будем понимать совокупность взаимосвязанных конструктивно независимых изделий, которые обладают свойством перестраивать свою структуру в результате случайного повреждения некоторых её элементов без нарушения (либо частичного нарушения) выполняемой перед ней задачи.
Аналогом элемента с тремя несовместными состояниями в системах электроснабжения потребителей электроэнергии может быть представлен защитный коммутационный аппарат, который с течением времени может находиться в трех несовместных состояниях: работоспособном, отказавшем: отказ обрыв цепи
или отказ в срабатывании
.
Если в зоне действия релейной защиты (РЗ) i-того коммутационного аппарата произошло повреждение (КЗ или ОЗ) и оно было отключено соответствующим устройством, то такие повреждения следует относить к отказам обрыв цепи
.
Ложное (излишнее) срабатывание РЗ, а также ошибки обслуживающего и эксплуатирующего персонала, при которых отключаются i-тые защитные коммутационные аппараты, также следует относить к отказам обрыв цепи
.
К отказам в срабатывании
i-того защитного коммутационного аппарата следует относить также повреждения в защищаемой сети, при которых через него проходит сквозной аварийный ток, а его РЗ не работает (находится в отказавшем состоянии).
Секционный i-тый коммутационный аппарат снабжен АВР и в нормальном состоянии отключен.
К отказам обрыв цепи
i-того секционного коммутационного аппарата следует относить следующие события: при аварийном автоматическом отключении вводного защитного коммутационного аппарата с помощью реле минимального напряжения, секционный коммутационный аппарат не включился.
Аварийное включение i-того секционного коммутационного аппарата с помощью АВР на КЗ, в результате чего через него прошел сквозной аварийный ток, а его токовая защита не работает, то это событие следует относить к отказу в срабатывании
.
Для оценки надежности систем электроснабжения широкое распространение получили элементные методы [2].
В этих методах предполагается, что электрооборудование в схемах замещения систем электроснабжения состоит из самостоятельных (в смысле анализа надежности) элементов.
Под узлами
схемы замещения понимаются физические пункты, которые непосредственно связаны не менее чем с тремя направлениями передачи энергии, т.е. обычно это сборные шины или секции распределительных пунктов [5].
Используя принципиальную схему системы электроснабжения, составляется схема замещения для оценки надежности потребителей, которые получают электроэнергию от рассматриваемого узла
нагрузки.
Все независимые источники электроснабжения системы объединяются в одну точку: она считается абсолютно
надежной и является входом
схемы замещения [6].
Все повреждения в схеме электроснабжения выше выбранной точки входа
в расчетах не учитываются.
Под элементом i, i = (1÷n) в схеме замещения системы электроснабжения будем понимать совокупность оборудования: защитный коммутационный аппарат и электрооборудование, которое входит в зону действия его (РЗ).
Выходом
схемы замещения системы электроснабжения являются сборные шины, от которых получают электроэнергию потребители.
Если отказ i-того элемента (отказ типа обрыв цепи
) не влияет на работоспособность граничных ему узлов
, то в этом случае расчетная схема замещения совпадает с электрической [5].
3.1 Алгоритм получения минимальных сечений
при учете отказов элементов схемы замещения типа обрыв цепи
Предположим, что все рассматриваемые элементы, из которых состоит система электроснабжения могут отказывать независимо друг от друга; каждый элемент может находится в трех несовместимых состояниях: работоспособном, неработоспособном – отказ обрыв цепи
, неработоспособном – отказ в срабатывании
; потоки отказов элементов обрыв цепи
и отказ в срабатывании
простейшие; пропускная способность элементов не ограничена, так же как и способность сдерживать поток электроэнергии независимо от количества короткозамкнутых элементов, после выхода из строя элемент не восстанавливается (не заменяется на новый) в рассматриваемый период времени.
Обозначим через рi – вероятность безотказной работы i-того элемента системы, – вероятность появления отказов в i-том элементе типа обрыв цепи
, а через – вероятность появления отказов в i-том элементе типа отказ в срабатывании
. Эти три состояния составляют полную группу несовместных событий:

Индексы о
и s
в формуле (1) указывают на то, что учитываются повреждения элемента, которые приводят к отказам обрыв цепи
либо отказам в срабатывании
соответственно.
В том случае, если в элементах системы электроснабжения наблюдается два типа несовместных отказов: отказ обрыв цепи
и отказ в срабатывании
, тогда вероятность отказов элемента i с учетом двух типов отказов, в течение времени t можно определить пользуясь формулами [8]:


где λoi, λsi – постоянные интенсивности отказов i-того элемента при учете его отказов типа обрыв цепи
и отказов в срабатывании
соответственно;
t – текущее время работы i-того элемента системы.
Интенсивность отказов i-того элемента системы:


где noi, nsi – число выявленных аварийных отключений i-того элемента системы при учете его отказов типа обрыв цепи
и отказов в срабатывании
;
Ti – время наблюдения за i-тым элементом системы;
Ni – число i однотипных элементов, которые находятся под наблюдением.
Под простой
по структуре схемой замещения исходной системы будем понимать такую, элементы которой могут соединяться: последовательно, параллельно, последовательно-параллельно либо параллельно-последовательно.
Для простой по определению схемы замещения системы, которая состоит из n
логически последовательного соединения элементов, отказ типа обрыв цепи
любого из i
элементов (i = (1÷n)), приводит к разрыву связи между ее узлами
вход
и выход
.
Если заданы вероятности отказов элементов схемы замещения qoi, то вероятность Qo разрыва связи между узлами
вход
и выход
определим следующим образом:

В том случае, если у каждого из n
логически последовательно соединенных элементов произойдет отказ в срабатывании
в каждом из i
элементов, то это приведет к тому, что между узлами
вход
и выход
схемы замещения пройдет сквозной аварийный ток.
Если заданы вероятности отказов элементов схемы замещения qsi, то вероятность Qs того, что между точкой вход
и выход
схемы замещения пройдет сквозной аварийный ток, найдем с помощью формулы:

Для простой по определению схемы замещения системы, которая состоит из m
логически параллельно соединенных элементов, отказ типа обрыв цепи
в каждом из j
элементе (j = (1÷m)) приводит к разрыву связи между узлами
вход
и выход
.
Если заданы вероятности отказов элементов схемы замещения qoi, то вероятность Qo того, что произойдет разрыв связи между узлами
вход
и выход
, определим с помощью формулы:

В том случае, если у любого из m
логически параллельного соединения элементов произойдет отказ в срабатывании
, то это приведет к тому, что между узлами
вход
и выход
схемы замещения пройдет сквозной аварийный ток.
Если заданы вероятности отказов qsi, (j = (1÷m)) элементов схемы замещения, которая состоит из m
логически параллельного соединения элементов, тогда вероятность Qs того, что между узлами
вход
и выход
схемы замещения пройдет сквозной аварийный ток, найдем, используя формулу:

Под сложной
по структуре схемой замещения системы будем понимать такую, в состав которой входит хотя бы одна группа элементов соединенных в виде логической звезды
или треугольника
.
Под вероятностью безотказной работы невосстанавливаемой системы, элементы которой могут находиться в трех несовместных состояниях, будем понимать меру ее надежности, которая характеризуется вероятностью того, что в течение заданного интервала времени не произойдут такие случайные события, в результате которых разрывается связь или пройдет сквозной аварийный ток между точками вход
и выход
схемы замещения, при условии, что в начальный момент времени все ее элементы находились в работоспособном состоянии.
Для нахождения нижней оценки Rн вероятности безотказной работы невосстанавливаемой системы справедливо соотношение:

где Rн – нижняя оценка вероятности того, что не произойдут такие случайные события, в результате которых разорвется связь или пройдет сквозной аварийный ток между узлами
вход
и выход
схемы замещения.
Qoн и Qsн – нижняя оценка вероятности того, что произойдет разрыв связи или пройдет сквозной аварийный ток между узлами
вход
и выход
схемы замещения соответственно.
Для приведения сложной
схемы замещения, элементы которой подвергаются отказам типа обрыв цепи
, к простой
, воспользуемся понятием сечение
и минимальное сечение
[1].
Сложную
по определению схему замещения системы, при учете двух несовместных типов отказов, можно заменить на две эквивалентные по надежности простые
, используя понятие сечение
и минимальное сечение
.
Под отказом сложное по определению схемы замещение системы, при учете отказов ее элементов типа обрыв цепи
будем понимать появление такого случайного события, в результате которого происходит повреждение некоторых ее элементов и прерывается связь между ее узлами вход
и выход
(между источниками энергосбережения и его потребителями).
Под сечением
C
схемы замещения сложной
системы будем понимать совокупность элементов, выход из строя которых (отказ типа обрыв цепи
) приводит к разрыву связи между узлами
вход
и выход
.
Под минимальным сечением
Cmin
схемы замещения сложной
системы будем понимать сечение
, у которого предполагается, что хотя бы один элемент оказался абсолютно надежным, в результате чего отказы типа обрыв цепи
оставшихся в этом сечении
элементов не будет более составлять сечение
, так как при этом не происходит разрыв связи между узлами
вход
и выход
.
Используя исходную схему замещения сложной
структуры, понятие минимальное сечение
Cmin
, учитывая, что элементы системы подвергаются отказам типа обрыв цепи
и если заданы вероятности отказов каждого из i
элементов qoi (i = (1÷n)), строятся схемы минимальных сечений
.
При построении схемы замещения минимальных сечений
Cmin
при учете отказов элементов типа обрыв цепи
, выделяют отдельно одно-, двух- и трехэлементные и т.д. (минимальные сечения
). После получения отдельных групп минимальных сечений
их соединяют последовательно между собой, начиная от минимального сечения
, которое состоит из одного или двух параллельно соединенных элементов и заканчивая минимальным сечением
, которое состоит из максимально возможного числа параллельно соединенных элементов.
Используя простую
по определению схему замещения минимальных сечений
, формулы (6) и (8), определяем нижнюю оценку ее вероятности отказов Qoн.
Под отказом сложной
схемы замещения системы, при учете отказов в срабатывании
элементов, будем понимать появление такого случайного события, в результате чего между узлами
вход
и выход
схемы замещения протекает сквозной аварийный ток.
Под сечением

сложной
схемы замещения системы будем понимать совокупность элементов, выход из строя которых (учитываются отказы в срабатывании
элементов схемы замещения) приводит к тому, что между узлами вход
и выход
схемы замещения протекает сквозной аварийный ток.
Под минимальным сечением
 сложной схемы замещения системы будем понимать
сложной схемы замещения системы будем понимать сечение
, у которого предполагаем, что хотя бы один элемент оказался абсолютно надежным, в результате чего отказы в срабатывании
оставшихся в этом сечении
элементов уже не будет более составлять сечение
, так как при этом не происходит протекание сквозного аварийного тока между узлами
вход
и выход
.
Используя исходную схему замещения сложной
системы понятия  учитывая, что в элементах системы наблюдаются отказы в
учитывая, что в элементах системы наблюдаются отказы в срабатывании
и известны вероятности отказов каждого из ее i
элементов qsi, построим схему минимальных сечений
следующим образом.
Каждое минимальное сечение
представляет собой минимальный набор логически последовательного соединения элементов, отказ которых (учитываются отказы в срабатывании
элементов) приводит к тому, что происходит протекание сквозного аварийного тока между узлами
вход
и выход
схемы замещения системы.
Все полученные минимальные сечения
соединяются между собой в параллельную группу, в результате чего получим простую
по определению схему замещения минимальных сечений
системы, при учете отказов в срабатывании
ее элементов.
Используя простую
по определению схему замещения минимальных сечений
, при учете отказов в срабатывании
ее элементов, формулы (7) и (9), находим нижнюю оценку ее вероятности отказов Qsн.
Исходными данными для построения схемы минимальных сечений
(учитывая отказы элементов схему замещения типа обрыв цепи
) являются: схема замещения системы с указанием всех ее узлов; номера элементов, которые соединяют узлы между собой; выделены вход
и выход
; вероятности безотказной работы элементов qoi (i = (1÷n)).
Для построения схемы замещения минимальных сечений
следует заполнить (табл. 1) следующим образом:
- в колонку 1 первой строки (№1) ставим символ Ао – узел, который обозначает
вход
в схеме замещения; - в колонку 2 первой строки записываются номера элементов схемы замещения непосредственно связанных с узлом Ао;
- в колонку 3 записываются эти же номера элементов схемы замещения, которые и являются
сечением
, его же заносят в колонку 4, т.к. этосечение
будетминимальным
(по определению). - в колонку 1 второй строки №2 ставим
узел
Ао и Аj, которые соединяются между собой с помощью элемента j, (j = (1÷n)), где n – число элементов в схеме замещения непосредственно связанных сузлом
Ао; - в колонку 2 ставим столбец, который состоит из двух строк: в верхнюю строку записываем номера элементов схемы замещения, которые соединяются с узлом Ао, а во вторую строку записываются номера элементов, которые непосредственно соединяют узел Аj с другими узлами;
- одинаковые номера элементов схемы замещения, которые входят в первую и вторую строки, вычеркиваем и получаем
сечение
. Полученное таким образомсечение
заносим в колонку 3, затем его анализируем. Если полученноесечение
являетсяминимальным
(по определению), то его заносят в колонку 4, если нет, то четвертая колонка остается не заполненной (т.е. такогоминимального сечения
не существует). - после установления всех связей между узлами Ао и Аj и построения
минимальных сечений
, к этой группе прибавляетсяузел
Аi (i = (1÷n)), который через элемент j схемы замещения связан с узлом Аj или он связан элементом с узлом Ао (имеет место при числе элементов, непосредственно связанных с Ао, n ≥ 3) и процедура полученияминимального сечения
повторяется, т.е. в колонку один заносятся узлы Ао, Аj, Аi; - в колонку 2 заносят столбец, который состоит из трех строк: в первую строку записываются номера элементов схемы замещения, которые соединяются с узлом Ао, а во вторую – элементы, которые соединяются с узлом Аj и в третью – элементы, которые соединяются с узлом Аi;
- четное число одинаковых номеров элементов, которые входят в разные строки – вычерчиваются, полученное
сечение
записывается в колонку 3 и после его анализа, если оно являетсяминимальным
(по определению), то его записывают в колонку 4; - описанная выше процедура получения
минимальных сечений
будет повторяться до тех пор, пока в первую колонку (табл. 1) не будет внесены всеузлы
схемы замещения без последнего, который обозначаетвыход
схемы замещения, а затем составляются столбцы из строк, каждая из которых состоит из номеров элементов, соединяющихся с данным узлом; - вычеркиваем четное число номеров элементов схемы замещения, которые выходят в разные строки, а затем получаем последнее
минимальное сечение
; - номера элементов каждой строки (табл. 1) колонки 4 соответсвуют определенному
минимальному сечению
, которое представляется в виде их параллельного соединения (отказ элементов данногоминимального сечения
приводит к тому, что связь между узломвход
ивыход
будет нарушена); - последовательное соединение
минимальных сечений
позволяет получить расчетную схему для определения нижней оценки вероятности отказов системы при учете отказов ее элементов типаобрыв цепи
.
Таблица 1 – Алгоритм получения минимальных сечений
при учете отказов элементов схемы замещения типа обрыв цепи
| № | Узел схемы замещения | Элементы связи между узлами | Сечение |
Минимальное сечение |
| 0 | 1 | 2 | 3 | 4 |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| ⋮ | ||||
| n |
3.2 Алгоритм получения минимальных сечений
при учете отказов в срабатывании
элементов схемы замещения
Для получения схемы замещения минимальных сечений
, при учете отказов в срабатывании
ее элементов следует заполнить (табл. 2), используя следующие правила:
Таблица 2 – Алгоритм получения минимальных сечений
при учете отказов в срабатывании
элементов схемы замещения
| № | Минимальное число узловмежду входомАо и выходомАn |
Элементы связи между узлами, i | Сечение |
Минимальное сечение |
| 0 | 1 | 2 | 3 | 4 |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| ⋮ | ||||
| n |
- в первый столбец первой строки (табл. 2) заносится минимальное число узлов схемы замещения, начиная с Ао – узел
входа
и заканчивая узломвыхода
– Аn, (i = (1÷n)), через которые может пройти сквозной аварийный ток; - во второй столбец первой строки (табл. 2) записываются номера элементов схемы замещения, которые соединяют между собой отдельные узлы, занесенные в первый столбец первой строки;
- в третий столбец первой строки (табл.2) записываем номера элементов второго столбца первой строки, повреждения которых (отказ в
срабатывании
) приводят к тому, что через узел Ао и Аn, пройдет сквозной аварийный ток, т.е. получитсясечение
; - анализируем полученное
сечение
: если оно получилосьминимальным
(по определению), то номера его элементов записываем в колонку 4 первой строки, а если нет, четвертая колонка остается не заполненной, т.е. такогоминимального сечения
не существует; - после получения первого
минимального сечения
процедура повторяется до тех пор, пока не будет перечислены все существующие в приведенной схеме замещенияминимальные сечения
; - каждое получаемое
минимальное сечение
(табл. 2), четвертый столбец представляется в виде последовательно соединенных элементов (номера элементов занесены в строку, колонка 4); - параллельное соединение всех полученных
минимальных сечений
позволяет получить расчетную схему для определения нижней оценки вероятности отказов системы при учете отказов всрабатывании
ее элементов.
Используя полученные алгоритмы построения схем минимальных сечений
с учетов двух несовместимых типов отказов элементов схемы замещения (отказ обрыв цепи
и отказ в срабатывании
) – составляются схемы минимальных сечений
. Используя формулы (6), (8) и (7), (9), вероятности qoi, qsi, (i = (1÷n)) элементов схемы замещения, представляется возможность определить нижнюю оценку Qoн вероятности того, что не произойдет разрыв между узлом
вход
и выход
схемы замещения и Qsн вероятности того, что между узлом
вход
и выход
схемы замещения пройдет сквозной аварийный ток.
Нижнюю оценку вероятности Rн того, что не произойдет разрыв связи или не пройдет сквозной аварийный ток между узлами
вход
и выход
схемы замещения определяется с помощью формулы (10).
Описанная выше методика построения схем замещения минимальных сечений
позволяет оценивать надежность сложных систем, элементы которых могут находиться в трех несовместимых состояниях.
4. Практический раздел
Схема замещения сложной системы, для оценки ее надежности приведена на рис. 1:

Рисунок 1 – Схема замещения системы
(анимация: 8 кадров, 3 цикла повторения, 75 килобайт)
Для элементов схемы замещения (рис.1) заданы следующие интенсивности отказов: λo1 = 0,58 год−1; λs1 = 0,34 год−1; λo2 = 0,42 год−1; λs2 = 0,25 год−1; λo3 = 0,75 год−1; λs3 = 0,25 год−1; λo4 = 0,5 год−1; λs4 = 0,34 год−1; λo5 = 0,75 год−1; λs5 = 0,25 год−1; λo6 = 0,34 год−1; λs6 = 0,25 год−1; λo7 = 0,67 год−1; λs7 = 0,5 год−1; λo8 = 0,5 год−1; λs8 = 0,42 год−1.
Определить нижнюю оценку Rн того, что в течение времени t = 0,1 год не произойдет разрыв связи или не пройдет сквозной аварийный ток между узлами вход
и выход
схемы замещения.
Используя формулы (2) и (3), исходные данные примера, для t = 0,1 год находим qoi, qsi (i = (1÷8)): qo1 = 0,0554; qs1 = 0,0325; qo2 = 0,0406; qs2 = 0,0242; qo3 = 0,0714; qs3 = 0,0238; qo4 = 0,0479; qs4 = 0,0326; qo5 = 0,0714; qs5 = 0,0238; qo6 = 0,033; qs6 = 0,0243; qo7 = 0,0632; qs7 = 0,0472; qo8 = 0,0478; qs8 = 0,0401.
Для получения схемы минимальных сечений
(учитываются отказы элементов типа обрыв цепи
), используем схему рис. 1 и заполняется табл. 3 в соответствии с описанным выше алгоритмом.
Таблица 3 – Алгоритм получения минимальных сечений
при учёте отказов схемы типа обрыв цепи
| № | Узел схемы замещения | Элементы связи между узлами | Сечение |
Минимальное сечение |
| 1 | 2 | 3 | 4 | |
| 1 | Ао | 1,2,3 | 1.2.3 | 1.2.3 |
| 2 | Ао+А1 | 1, |
1.3.4.7 | 1.3.4.7 |
| 3 | Ао+А2 | 1,2, |
1.2.6.7.8 | 1.2.6.7.8 |
| 4 | Ао+А3 | 2.3.4.5.6 | 2.3.4.5.6 | |
| 5 | АоА1+А3 | 3.5.6.7 | 3.5.6.7 | |
| 6 | АоА1+А2 | 1, |
1.4.6.8 | 1.4.6.8 |
| 7 | АоА2+А3 | 2.4.5.7.8 | — | |
| 8 | АоА1А3+А2 | 3,5,6,7 3,6,7,8 |
5.8 | 5.8 |
Сечение №7 (2.4.5.7.8) не является минимальным, так как включает в себя уже минимальное сечение
(5.8), поэтому колонка 4 в этом случае остается пустой.
Используя полученную четвертую колонку (табл. 3), строим схему минимальных сечений
, располагая их сечения следующим образом:
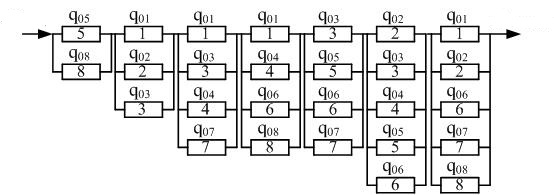
Рисунок 2 – Схема минимальных сечений
при учете отказов элементов обрыв цепи
Для получения схемы минимальных сечений
(учитывается отказ в срабатывании
элемента), следует использовать схему рис. 1 и заполнить табл. 4 в соответствии с описанным выше правилом.
Таблица 4 – Алгоритм получения минимальных сечений
при учёте отказов элементов в срабатывании
| № | Узлы схемы, через которые проходит сквозной аварийный ток | Элементы связи между узлами | Сечение |
Минимальное сечение |
| 1 | 2 | 3 | 4 | |
| 1 | Ао; А2; А4 | 3,7 | 3.7 | 3.7 |
| 2 | Ао; А3; А4 | 1,6 | 1.6 | 1.6 |
| 3 | Ао; А3; А2; А4 | 1,6,8 | 1.6.8 | 1.6.8 |
| 4 | Ао; А1; А3; А4 | 2,4,5 | 2.4.5 | 2.4.5 |
| 5 | Ао; А1; А2; А4 | 2,7,8 | 2.7.8 | 2.7.8 |
| 6 | Ао; А2; А3; А4 | 3,6,5 | 3.6.5 | 3.6.5 |
| 7 | Ао; А1; А3; А2; А4 | 2,4,6,8 | 2.4.6.8 | 2.4.6.8 |
| 8 | Ао; А2; А1; А3; А4 | 3,7,4,5 | 3.7.4.5 | 3.7.4.5 |
| 9 | Ао; А3; А1; А2; А4 | 1,4,7,8 | 1.4.7.8 | 1.4.7.8 |
| 10 | Ао; А1; А2; А3; А4 | 2,7,6,5 | 2.7.6.5 | 2.7.6.5 |
Используя данные табл. 4, колонка 4 строим схему минимальных сечений
(учитываются отказы в срабатывании
ее элементов):
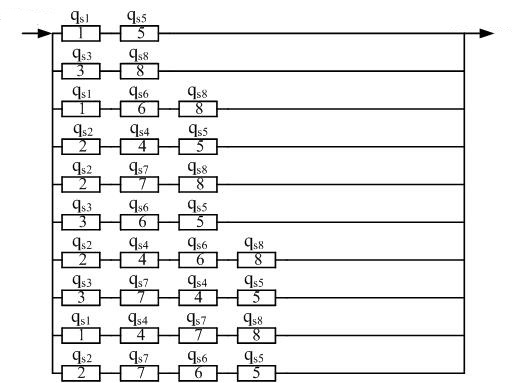
Рисунок 3 – Схема минимальных сечений
при учете отказов в срабатывании
элементов
Используя схемы замещения минимальных сечений
, рис. (2 и 3), формулы (6), (8), (7), (9) находим:
Подставим значения qoi(0,1), qsi(0,1), (i = (1÷8)) в полученные формулы, находим:
Используя формулу (10) находим:
Аналогичный результат был получен при решении этой же задачи, используя метод преобразования треугольник–звезда
и звезда–треугольник
[9], т.е.  = 0,9946. Аналогичный результат был получен, если поставленную задачу решать точными методами, основанном на использовании понятия алгебры кортежей [10] и используя логико-вероятностный метод [7], т.е. и в этих случаях: R = 0,9946.
= 0,9946. Аналогичный результат был получен, если поставленную задачу решать точными методами, основанном на использовании понятия алгебры кортежей [10] и используя логико-вероятностный метод [7], т.е. и в этих случаях: R = 0,9946.
Выводы
- Предложен один из возможных способов оценки надежности структурно-сложных по структуре невосстанавливаемых систем, элементы которых могут находиться в трех несовместных состояниях.
- Если не учитывать в расчетах надежность невосстанавливаемых систем отказы в
срабатывании
защитных коммутационных аппаратов, т.е. Qsн = 0, тогда, для данного конкретного примера, надежность системы завышается в 2 раза. - Точность расчетов надежности невосстанавливаемых структурно-сложных схем для t ≤ 0,1 год, предлагаемым способом с использованием схем
минимальных сечений
не отличается от известных. - Предложенный способ оценки надежности сложных невосстанавливаемых систем, элементы которых могут находиться в трех несовместных состояниях, основан на простых и понятных инженеру понятиях и может быть использован для подготовки инженеров-электриков любых специальностей.
На момент написания данного реферата магистерская работа еще не завершена. Ориентировочная дата завершения магистерской работы: июнь 2019 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Список используемой литературы
- Беляев Ю. К. Надежность технических систем: Справочник [текст] / Ю. К. Беляев, В. А. Богатырев, В. В. Болотин и др., Под ред. И. А. Ушакова. – М.: Радио и связь. – 1985 – 608 с.
- Рябинин И. А. Надежность и безопасность структурно-сложных систем [текст] / И. А. Рябинин. – С.П.Б. Изд-во С.–Петербург. ун-та. – 2008. – 276 с.
- Ковалев А. П. О преобразовании
Звезда
–треугольник
при расчетах надежности сложных по структуре схем [текст] / А. П. Ковалев, А. В. Спиваковский // Электричество. – №10. – 1998. – с.70–74. - Эндрени Дж. Моделирование при расчетах надежности в электроэнергитических системах: [текст] / Дж. Эндрени. Пер. с англ / Под ред Ю. Н. Руденко. – М.: Энергоатомиздат. – 1983. – 336.
- Фокин Ю. А. Расчет надежности систем энергоснабжения [текст] / Ю. А. Фокин, А. М. Харченко // Электричество – №8. – 1982. – с. 5–10.
- Белоусенко И. В. О расчете надежности систем электроснабжения газовых промыслов [текст] / И. В. Белоусенко, М. С. Ершов, А. П. Ковалев, В. В. Якимишина, О. А. Шевченко // Электричество. – №3. – 2004. с. 23–28.
- Ковалев А. П. Применение логико-вероятностных методов для оценки надежности структурно-сложных систем [текст] / А. П. Ковалев, А. В. Спиваковский // Электричество. – 2000. – №9. – с. 66–70.
- Диллон Б. Инженерные методы обеспечения надежности систем [текст] / Б. Диллон, Ч. Сингх. Пер. с англ. – М.: Мир. – 1984. – 318 с.
- Ковалев А. П. Расчет надежности невосстанавливаемых систем, элементы которых могут находиться в трех несовместных состояниях [текст] / А. П. Ковалев, И. И. Москвина, Т. Г. Бусыгин // Промышленная энергетика. – 2018. – №3. – с. 7–13
- Кулик Б. А. Логико-вероятностные методы на алгебре кортежей. – В сб.: Теория информационная техника моделирование безопасности сложных систем – С.П.Б.: ИПМ РАН. 1995. Вып.5, Препринт 123, с. 18–43.
