Русский   English

Реферат за темою випускної роботи

Зміст

Вступ

Елементи з трьома несумісними станами: працездатне, відмова типу обрив кола і відмова типу коротке замикання можна виділити в системах: електропостачання, газопостачання, водопостачання і т.д. Аналогами елементів з трьома несумісними станами в таких системах можуть бути захисні комутаційні апарати, крани, вентилі різних типів, запірна арматура, заглушки і інші види переривників потоку (електроенергії, газу, рідини, інформації і т.д.), для яких в непрацездатному стані потік не переривається (коротке замикання) або не передається (обрив кола) [3].

У тих випадках, якщо необхідно підвищити надійність проектованої системи без зміни надійності комплектуючих її елементів зазвичай вводять надлишкові (резервні) елементи, або змінюють структурну схему мережі. Для систем, що складаються з елементів, які можуть перебувати в трьох несумісних станах, введення надлишкових елементів з трьома станами може не тільки не збільшити її надійність, але навіть знизити. Все буде залежати від співвідношення між різними видами відмов елемента схеми, її конфігурації і числа резервних елементів або їх груп.

1. Актуальність теми

Розробка нових та удосконалення існуючих методів оцінки надійності невідновлюваних систем, елементи яких можуть знаходитися в трьох несумісних станах, є актуальною науковою проблемою, вирішення якої дозволить значно підвищити точність прогнозу їх надійності, як на етапі проектування, так і на етапі реконструкції та експлуатації.

2. Мета і завдання дослідження, плановані результати

Метою магістерської роботи є огляд одного з існуючих методів оцінки надійності невідновлюваних, складних за структурою систем, елементи яких можуть знаходитися в трьох несумісних станах – методу Мінімальних перетинів.

Основні завдання дослідження:

  1. Огляд літературних джерел і визначення існуючих методів оцінки надійності невідновлюваних, складних за структурою систем, елементи яких можуть знаходитися в трьох несумісних станах.
  2. Розбір методу Мінімальних перетинів.
  3. Застосування даного методу розрахунку на конкретному прикладі.

Плановані результати:

  1. Визначення точності розрахунку надійності невідновлювальних структурно-складних схем для t ≤ 0,1 рік, пропонованим способом з використанням схем мінімальних перетинів.
  2. Порівняння точності розрахунку з іншими відомими методами розрахунку оцінки надійності невідновлюваних систем, елементи яких можуть знаходитися в трьох несумісних станах.

3. Практичний розділ

Схема заміщення складної системи, для оцінки її надійності наведена на рис. 1:

Схема замещения системы

Рисунок 1 – Схема заміщення системи
(анімація: 8 кадрів, 3 цикла повторення, 75 кілобайт)

Для елементів схеми заміщення (рис.1) задані наступні інтенсивності відмов: λo1 = 0,58 рік−1; λs1 = 0,34 рік−1; λo2 = 0,42 рік−1; λs2 = 0,25 рік−1; λo3 = 0,75 рік−1; λs3 = 0,25 рік−1; λo4 = 0,5 рік−1; λs4 = 0,34 рік−1; λo5 = 0,75 рік−1; λs5 = 0,25 рік−1; λo6 = 0,34 рік−1; λs6 = 0,25 рік−1; λo7 = 0,67 рік−1; λs7 = 0,5 рік−1; λo8 = 0,5 рік−1; λs8 = 0,42 рік−1.

Визначити нижню оцінку Rн того, що протягом часу t = 0,1 рік не відбудеться розрив зв'язку або не пройде наскрізний аварійний струм між вузлами вхід і вихід схеми заміщення.

Використовуючи формули (2) і (3), вихідні дані прикладу, для t = 0,1 рік знаходимо qoi, qsi (i = (1÷8)): qo1 = 0,0554; qs1 = 0,0325; qo2 = 0,0406; qs2 = 0,0242; qo3 = 0,0714; qs3 = 0,0238; qo4 = 0,0479; qs4 = 0,0326; qo5 = 0,0714; qs5 = 0,0238; qo6 = 0,033; qs6 = 0,0243; qo7 = 0,0632; qs7 = 0,0472; qo8 = 0,0478; qs8 = 0,0401.

Для отримання схеми мінімальних перетинів (враховуються відмови елементів типу обрив кола), використовуємо схему рис. 1 і заповнюється табл. 1 відповідно до описаного вище алгоритма.


Таблиця 1 – Алгоритм отримання мінімальних перетинів при врахуванні відмов схеми типу обрив кола

№ Вузол схеми заміщення Елементи зв'язку між вузлами Перетин Мінімальний перетин
1 2 3 4
1 Ао 1,2,3 1.2.3 1.2.3
2 Ао+А1 1,2,3
2,4,7		 1.3.4.7 1.3.4.7
3 Ао+А2 1,2,3
3,7,6,8		 1.2.6.7.8 1.2.6.7.8
4 Ао+А3 1,2,3
1,4,5,6		 2.3.4.5.6 2.3.4.5.6
5 АоА1+А3 1,3,4,7
1,4,5,6		 3.5.6.7 3.5.6.7
6 АоА1+А2 1,3,4,7
3,6,7,8		 1.4.6.8 1.4.6.8
7 АоА2+А3 1,2,6,7,8
1,4,5,6		 2.4.5.7.8 —
8 АоА1А3+А2 3,5,6,7
3,6,7,8		 5.8 5.8


Перетин №7 (2.4.5.7.8) не є мінімальним, так як включає в себе вже мінімальний перетин (5.8), тому колонка 4 в цьому випадку залишається порожньою.

Використовуючи отриману четверту колонку (табл. 1), будуємо схему мінімальних перетинів, розташовуючи їх перетини наступним чином:

рисунок

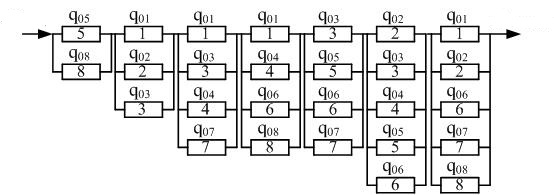
Рисунок 2 – Схема мінімальних перетинів при врахуванні відмов елементів обрив кола

Для отримання схеми мінімальних перетинів (враховується відмова в спрацьовуванні елемента), слід використовувати схему рис. 1 і заповнити табл. 2 відповідно до описаного вище правила.


Таблиця 2 – Алгоритм отримання мінімальних перетинів при врахуванні відмов елементів в спрацьовуванні

№ Вузли схеми, через які проходить наскрізний аварійний струм Елементи зв'язку між вузлами Перетин Мінімальний перетин
1 2 3 4
1 Ао; А2; А4 3,7 3.7 3.7
2 Ао; А3; А4 1,6 1.6 1.6
3 Ао; А3; А2; А4 1,6,8 1.6.8 1.6.8
4 Ао; А1; А3; А4 2,4,5 2.4.5 2.4.5
5 Ао; А1; А2; А4 2,7,8 2.7.8 2.7.8
6 Ао; А2; А3; А4 3,6,5 3.6.5 3.6.5
7 Ао; А1; А3; А2; А4 2,4,6,8 2.4.6.8 2.4.6.8
8 Ао; А2; А1; А3; А4 3,7,4,5 3.7.4.5 3.7.4.5
9 Ао; А3; А1; А2; А4 1,4,7,8 1.4.7.8 1.4.7.8
10 Ао; А1; А2; А3; А4 2,7,6,5 2.7.6.5 2.7.6.5


Використовуючи дані табл. 2, колонка 4 будуємо схему мінімальних перетинів (враховуються відмови в спрацьовуванні її елементів):

рисунок

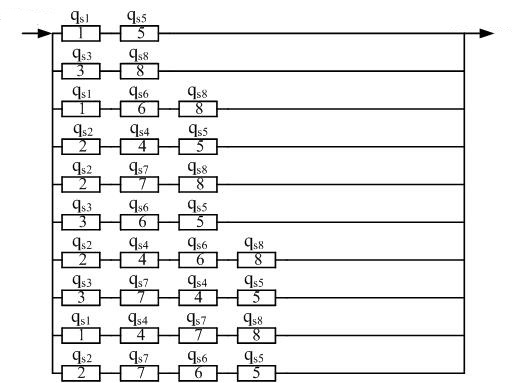
Рисунок 3 – Схема мінімальних перетинів при врахуванні відмов у спрацьовуванні елементів

Використовуючи схеми заміщення мінімальних перетинів, рис. (2 і 3), формули (6), (8), (7), (9) знаходимо:



Qoн = 1−(1−qo5qo8)(1−qo1qo2qo3)(1−qo1qo3qo4qo7)(1−qo1qo4qo6qo8)(1−qo3qo5qo6qo7)(1−qo2qo3qo4qo5qo6)(1−qo1qo2qo6qo7qo8);


Qsн = 1−(1−qs1qs5)(1−qs3qs8)(1−qs1qs6qs8)(1−qs2qs4qs5)(1−qs2qs7qs8)(1−qs3qs6qs5)(1−qs2qs4qs6qs8)(1−qs3qs7qs4qs5)(1−qs1qs4qs7qs8)(1−qs2qs7qs6qs5).


Підставимо значення qoi(0,1), qsi(0,1), (i = (1÷8)) в отримані формули, знаходимо:



Qoн = 0,0036; Qsн = 0,0018.


Використовуючи формулу (10) знаходимо:



R = 1−Qoн−Qsн = 1−0,0036−0,0018 = 0,9946.


Аналогічний результат був отриманий при вирішенні цього ж завдання, використовуючи метод перетворення трикутник–зірка і зірка–трикутник [9], тобто формула = 0,9946. Аналогічний результат був отриманий, якщо поставлене завдання вирішувати точними методами, заснованому на використанні поняття алгебри кортежів [10] і використовуючи логіко-імовірнісний метод [7], тобто і в цих випадках: R = 0,9946.

Висновки

  1. Запропонован один із можливих способів оцінки надійності структурно-складних за структурою невідновлювальних систем, елементи яких можуть знаходитися в трьох несумісних станах.
  2. Якщо не враховувати в розрахунках надійність невідновлювальних систем відмови в спрацьовуванні захисних комутаційних апаратів, тобто Qsн = 0, тоді, для даного конкретного прикладу, надійність системи завищується в 2 рази.
  3. Точність розрахунків надійності невідновлювальних структурно-складних схем для t ≤ 0,1 рік, пропонованим способом з використанням схем мінімальних перетинів не відрізняється від відомих.
  4. Запропонований спосіб оцінки надійності складних невідновлювальних систем, елементи яких можуть знаходитися в трьох несумісних станах, заснован на простих і зрозумілих інженерові поняттях і може бути використаний для підготовки інженерів-електриків будь-яких спеціальностей.

На момент написання даного реферату магістерська робота ще не завершена. Орієнтовна дата завершення магістерської роботи: червень 2019 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.

Перелік використаної літератури

  1. Беляев Ю. К. Надежность технических систем: Справочник [текст] / Ю. К. Беляев, В. А. Богатырев, В. В. Болотин и др., Под ред. И. А. Ушакова. – М.: Радио и связь. – 1985 – 608 с.
  2. Рябинин И. А. Надежность и безопасность структурно-сложных систем [текст] / И. А. Рябинин. – С.П.Б. Изд-во С.–Петербург. ун-та. – 2008. – 276 с.
  3. Ковалев А. П. О преобразовании Звезда–треугольник при расчетах надежности сложных по структуре схем [текст] / А. П. Ковалев, А. В. Спиваковский // Электричество. – №10. – 1998. – с.70–74.
  4. Эндрени Дж. Моделирование при расчетах надежности в электроэнергитических системах: [текст] / Дж. Эндрени. Пер. с англ / Под ред Ю. Н. Руденко. – М.: Энергоатомиздат. – 1983. – 336.
  5. Фокин Ю. А. Расчет надежности систем энергоснабжения [текст] / Ю. А. Фокин, А. М. Харченко // Электричество – №8. – 1982. – с. 5–10.
  6. Белоусенко И. В. О расчете надежности систем электроснабжения газовых промыслов [текст] / И. В. Белоусенко, М. С. Ершов, А. П. Ковалев, В. В. Якимишина, О. А. Шевченко // Электричество. – №3. – 2004. с. 23–28.
  7. Ковалев А. П. Применение логико-вероятностных методов для оценки надежности структурно-сложных систем [текст] / А. П. Ковалев, А. В. Спиваковский // Электричество. – 2000. – №9. – с. 66–70.
  8. Диллон Б. Инженерные методы обеспечения надежности систем [текст] / Б. Диллон, Ч. Сингх. Пер. с англ. – М.: Мир. – 1984. – 318 с.
  9. Ковалев А. П. Расчет надежности невосстанавливаемых систем, элементы которых могут находиться в трех несовместных состояниях [текст] / А. П. Ковалев, И. И. Москвина, Т. Г. Бусыгин // Промышленная энергетика. – 2018. – №3. – с. 7–13
  10. Кулик Б. А. Логико-вероятностные методы на алгебре кортежей. – В сб.: Теория информационная техника моделирование безопасности сложных систем – С.П.Б.: ИПМ РАН. 1995. Вып.5, Препринт 123, с. 18–43.